A Model of the Bat's Vertical Sweetness Gradient
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Printer-Friendly Version (PDF)
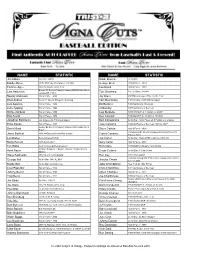
NAME STATISTIC NAME STATISTIC Jim Abbott No-Hitter 9/4/93 Ralph Branca 3x All-Star Bobby Abreu 2005 HR Derby Champion; 2x All-Star George Brett Hall of Fame - 1999 Tommie Agee 1966 AL Rookie of the Year Lou Brock Hall of Fame - 1985 Boston #1 Overall Prospect-Named 2008 Boston Minor Lars Anderson Tom Browning Perfect Game 9/16/88 League Off. P.O.Y. Sparky Anderson Hall of Fame - 2000 Jay Bruce 2007 Minor League Player of the Year Elvis Andrus Texas #1 Overall Prospect -shortstop Tom Brunansky 1985 All-Star; 1987 WS Champion Luis Aparicio Hall of Fame - 1984 Bill Buckner 1980 NL Batting Champion Luke Appling Hall of Fame - 1964 Al Bumbry 1973 AL Rookie of the Year Richie Ashburn Hall of Fame - 1995 Lew Burdette 1957 WS MVP; b. 11/22/26 d. 2/6/07 Earl Averill Hall of Fame - 1975 Ken Caminiti 1996 NL MVP; b. 4/21/63 d. 10/10/04 Jonathan Bachanov Los Angeles AL Pitching prospect Bert Campaneris 6x All-Star; 1st to Player all 9 Positions in a Game Ernie Banks Hall of Fame - 1977 Jose Canseco 1986 AL Rookie of the Year; 1988 AL MVP Boston #4 Overall Prospect-Named 2008 Boston MiLB Daniel Bard Steve Carlton Hall of Fame - 1994 P.O.Y. Philadelphia #1 Overall Prospect-Winning Pitcher '08 Jesse Barfield 1986 All-Star and Home Run Leader Carlos Carrasco Futures Game Len Barker Perfect Game 5/15/81 Joe Carter 5x All-Star; Walk-off HR to win the 1993 WS Marty Barrett 1986 ALCS MVP Gary Carter Hall of Fame - 2003 Tim Battle New York AL Outfield prospect Rico Carty 1970 Batting Champion and All-Star 8x WS Champion; 2 Bronze Stars & 2 Purple Hearts Hank -

Kit Young's Sale #131
page 1 KIT YOUNG’S SALE #131 1952-55 DORMAND POSTCARDS We are breaking a sharp set of the scarce 1950’s Dormand cards. These are gorgeous full color postcards used as premiums to honor fan autograph requests. These are 3-1/2” x 5-1/2” and feature many of the game’s greats. We have a few of the blank back versions plus other variations. Also, some have been mailed so they usually include a person’s address (or a date) plus the 2 cent stamp. These are marked with an asterisk (*). 109 Allie Reynolds .................................................................................. NR-MT 35.00; EX-MT 25.00 110 Gil McDougald (small signature) ..................................................................... autographed 50.00 110 Gil McDougald (small signature) ..............................................................................NR-MT 50.00 110 Gil McDougald (large signature) ....................................................... NR-MT 30.00; EX-MT 25.00 111 Mickey Mantle (bat on shoulder) ................................................. EX 99.00; GD watermark 49.00 111 Mickey Mantle (batting) ........................................................................................ EX-MT 199.00 111 Mickey Mantle (jumbo 6” x 9” blank back) ..................................................... EX-MT rare 495.00 111 Mickey Mantle (jumbo 6” x 9” postcard back) ................................................ GD-VG rare 229.00 111 Mickey Mantle (super jumbo 9” x 12” postcard back) .......................VG/VG-EX tape back 325.00 112 -

Baseball All-Time Stars Rosters
BASEBALL ALL-TIME STARS ROSTERS (Boston-Milwaukee) ATLANTA Year Avg. HR CHICAGO Year Avg. HR CINCINNATI Year Avg. HR Hank Aaron 1959 .355 39 Ernie Banks 1958 .313 47 Ed Bailey 1956 .300 28 Joe Adcock 1956 .291 38 Phil Cavarretta 1945 .355 6 Johnny Bench 1970 .293 45 Felipe Alou 1966 .327 31 Kiki Cuyler 1930 .355 13 Dave Concepcion 1978 .301 6 Dave Bancroft 1925 .319 2 Jody Davis 1983 .271 24 Eric Davis 1987 .293 37 Wally Berger 1930 .310 38 Frank Demaree 1936 .350 16 Adam Dunn 2004 .266 46 Jeff Blauser 1997 .308 17 Shawon Dunston 1995 .296 14 George Foster 1977 .320 52 Rico Carty 1970 .366 25 Johnny Evers 1912 .341 1 Ken Griffey, Sr. 1976 .336 6 Hugh Duffy 1894 .440 18 Mark Grace 1995 .326 16 Ted Kluszewski 1954 .326 49 Darrell Evans 1973 .281 41 Gabby Hartnett 1930 .339 37 Barry Larkin 1996 .298 33 Rafael Furcal 2003 .292 15 Billy Herman 1936 .334 5 Ernie Lombardi 1938 .342 19 Ralph Garr 1974 .353 11 Johnny Kling 1903 .297 3 Lee May 1969 .278 38 Andruw Jones 2005 .263 51 Derrek Lee 2005 .335 46 Frank McCormick 1939 .332 18 Chipper Jones 1999 .319 45 Aramis Ramirez 2004 .318 36 Joe Morgan 1976 .320 27 Javier Lopez 2003 .328 43 Ryne Sandberg 1990 .306 40 Tony Perez 1970 .317 40 Eddie Mathews 1959 .306 46 Ron Santo 1964 .313 30 Brandon Phillips 2007 .288 30 Brian McCann 2006 .333 24 Hank Sauer 1954 .288 41 Vada Pinson 1963 .313 22 Fred McGriff 1994 .318 34 Sammy Sosa 2001 .328 64 Frank Robinson 1962 .342 39 Felix Millan 1970 .310 2 Riggs Stephenson 1929 .362 17 Pete Rose 1969 .348 16 Dale Murphy 1987 .295 44 Billy Williams 1970 .322 42 -

Jim Parque's National Team Stats Bill Scott's National
The UCLA baseball program has sent eight players to play for the USA Baseball National Team a total of 10 times, beginning with the selection of Shane Mack in 1984. Most recently, former UCLA shortstop Brandon Crawford helped the U.S. National Team capture its second consecutive FISU (International University Sports Federation) World Championship in the summer of 2006. Crawford’s selection in 2006 marked the first time a Bruin had been named since Karp, a right-handed pitcher, competed for the national team in 2000. The 2006 U.S. National Team finished its summer campaign with a 28-2-1 mark and successfullyl defended its gold medal won in the 2004 FISU Tournament in Taiwan. UCLA’s student-athletes have not been the only individuals affiliated with the U.S. National Team. While working as an assistant coach at USC in the summer of 2000, current UCLA head coach John Savage served as an assistant to Mike Gillespie for the U.S. National Team of collegiate all-stars. UCLA Player Year(s) Brandon Crawford 2006 Josh Karp 1999, 2000 Bill Scott 1999 Jon Brandt 1999 Eric Valent 1997 Jim Parque 1996 Troy Glaus 1995, 1996 Shane Mack 1984 p Jim Parque’s National Team Stats YR ERA W-L G/GS CG SV IP H R ER BB SO OAV 1996 3.30 1-0 15/0 0 3 30.0 32 14 11 11 37 .274 Bill Scott’s National Team Stats u YR AVG GP-GS AB R H 2B 3B HR RBI BB SB-SBA OBP 1999 .340 36-34 141 31 48 8 2 9 32 8 4-6 .373 Jon Brandt’s National Team Stats p YR ERA W-L G/GS CG SV IP H R ER BB SO OAV 1999 7.12 1-2 9/4 0 0 30.1 38 28 24 13 26 .314 t Troy Glaus’s National Team Stats YR AVG GP-GS AB R H 2B 3B HR RBI BB SB-SBA OBP 1995 .306 35-27 111 19 34 3 0 2 15 10 0-1 .369 1996 .342 35-31 120 35 41 8 2 15 34 16 0-0 .423 Totals .324 70-58 231 54 75 11 2 17 49 26 0-1 .396 UCLA head coach John Savage served as pitching coach of the U.S. -

Water Supply Problem Badly Mishandled, Council Advised
THE WEATHER For Wisconsin: Showers tonight Observe Fire and Thursday. Cooler Thursday ex- cept in Milwaukee area. Prevention Local weather facts for 24 hours Wiscoiisiii Rapids Daily Tiilnme preceding 7 a. m.: Maximum 66; ff|j A CONSTRUJTl V E |ffa NEWS P^A P E R iO| Week, Oct. 3-9 minimum 47. Thirty-Fifth Year—No. 10,825 Wisconsin Rapids, Wis., Wednesday, October 6, 1948 Single Copy Five Cents 12 Fighter Planes Sain Shades Feller Hippity-Hop Over Pacific to Hawaii Water Supply Problem Badly In Pitching Duel Honolulu—(JP)—The navy sent 12 short range combat planes 2,426 miles across the Pacific yesterday | to prove a point. To Get Win, 1-0 The point: To deliver such air- craft over ocean distances beyond Braves Field, Boston—(>P)—Johnny Sain hurled the first 1-0 World Mishandled, Council Advised their fuel capacity by the shortest, Series shutout since 1923 today when he blanked Cleveland's Bobby Fel- quickest route, let them fly—with j ler, to give the Boston Braves the opening of the best-of-seven series refueling stops aboard conveniently I City Given Bad before some 39,000 fans. Sain, the rubber armed righthander with the fancy curve ball, out- spaced carriers. | Hog Market Deal on Wells, pitched the great Feller who allowed only two hits in a heart-breaking That's what the 12 fighters and Council Acts Favorably on loss. The Indians got four singles off Sain, a 24-game winner in the dive-torpedo bombers did—and for the first time. They hippity-hopped Committee Says regular season. -

Baseball World Series Game Tickets and Programs
Baseball World Series Game Tickets and Programs TICKETS 1931 World Series Cardinals at Athletics - Game 5 Ticket Stub Pepper Martin HR [VG-EX] PSA AUTH [Grades Very Good - Excellent, only minor edge and corner wear] 1935 World Series Tigers at Cubs - Game 5 Ticket Stub HR Chuck Klein WP Len Warneke PSA AUTH [Grades clean VgEx] 1936 World Series Giants at Yankees - Game 5 Ticket Stub NYG 5-4 (10) HR Selkirk PSA AUTH [Grades GOOD, creasing, surface wear, sl paper loss on rev corner] 1939 World Series Yankees at Reds - Game 3 Ticket Stub HR Joe DiMaggio, Bill Dickey [VG] PSA AUTH [Grades VG due to rough tear line] 1942 World Series Cardinals at Yankees - Game 5 Ticket Stub HR Phil Rizzuto Red Ruffing vs Johnny Beazley [G-VG] PSA AUTH [Grades G-VG due to rough tear line] 1942 World Series Cardinals at Yankees - Game 5 Ticket Stub HR Phil Rizzuto Yankees Win World Series PSA AUTH [Grades F-G; creasing] 1943 World Series Cardinals at Yankees - Game 2 Ticket Stub HR Marty Marion SP Walker Cooper PSA AUTH [Grades G-VG, minor creasing, rough tear line] 1949 World Series Yankees at Dodgers - Game 3 Ticket Stub HR Roy Campanella, Pee Wee Reese WP Joe Page [VG] PSA AUTH [Light creasing, displays much nicer] 1950 World Series Phillies at Yankees - Game 3 Ticket Stub NY 3-2 Ferrick vs Meyer PSA AUTH [Grades F/G; uneven tear line, creasing] 1952 World Series Dodgers at Yankees - Game 3 Ticket Stub BRK 5-3 HR Yogi Berra, Johnny Mize WP Preacher Roe PSA AUTH [Fair-Good; Vertical crease, sl paper loss, toning on reverse] 1952 World Series Dodgers at Yankees -

San Francisco Giants Weekly Notes: April 20-26
SAN FRANCISCO GIANTS WEEKLY NOTES: APRIL 20-26 Oracle Park 24 Willie Mays Plaza San Francisco, CA 94107 Phone: 415-972-2000 sfgiants.com sfgigantes.com giantspressbox.com @SFGiants @SFGigantes @SFGiantsMedia NEWS & NOTES GIANTS INTERVIEW SCHEDULE As an effort to keep Junior Giants connected while sheltering in place, the Giants Community Fund has announced the launch of Junior Giants At Home. Set to begin in May, the four-week virtual season will include home-produced videos from Gabe Monday - April 20 Kapler and his coaching staff to help introduce the fundamen- tals of the game along with important lessons in health, educa- 7:35 a.m. - Mike Krukow tion & character development. joins Murph & Mac Through his first 16 games in MLB The Show Players League, 5 p.m. - Gabe Kapler Giants OF Hunter Pence has gone 6-10 but has gone 4-1 in his joins Tolbert, Krueger & Brooks last five contests. Pence's next three games will take place to- Tuesday - April 21 morrow (Tuesday, April 21) where he'll face off with Tommy Kahnle (Yankees), Eduardo Ro- driguez (Boston) and David Dahl (Colorado). You can find the schedule by clicking here 7:35 a.m. - Duane Kuiper and watch them on Pence's Twitch channel here joins Murph & Mac The Giants have created sfgiants.com/fans/resource-center as a destination for updates re- 12 p.m. - Andrew Bailey garding the 2020 baseball season as well as a place to find resources that are being offered joins Papa & Lund throughout our communities during this difficult time. 4:30 p.m. -

Big Fantastic
2013 Honors 1 Autographed Limited Edition Per Box of a Current or Former Baseball Player(s)* Each is Enclosed in a Special PREMIUM Card Case with a Tamper Evident TRISTAR® Seal! The All Big Numbered to 25 or Less! 1 of 1 Find Fantastic Finds Single & Double Sided RARE Full Name Signature All 1 of 1s Including Joe DiMaggio Great Moments & Awards Satchel Paige 8 Double Sided SignaCutsTM Featuring a Joe DiMaggio Cut Signature and: Ted Williams, Arthur Miller, Ken Keltner, Al Gionfriddo, Ed Smith, Dolph Camilli, Bucky Walters & Bob Elliott Cut Signatures! Diamond Finds Hall of Fame Single & Double Sided Single & Double Sided All 1 of 1s Editions of 1, 5, 10 & 25 Casey Stengel(d) & Yasiel Puig Hank Aaron George & Ken Brett(d) Stan Musial(d) Leo Durocher(d) & Laraine Day(d) Happy Chandler(d) Ernie Banks/Starlin Castro Pee Wee Reese(d) Charles Gehringer(d) & Miguel Cabrera Don Drysdale(d) Duke Snider(d)/Matt Kemp And Many More! Heinie Manush(d) & Bryce Harper And Many More! One 1 of 1 Fantastic Find or Diamond Find & Five Hall of Famers per Case! Baseball Honors Double Play All Single Sided All Double Sided Editions of 1, 5, 10 & 25 Editions of 1, 5, 10 & 25 Mike Trout Don Larsen Mariano Rivera & Trevor Hoffman Craig Biggio Albert Pujols Bobby Richardson & Chuck Howley Evan Longoria Felix Hernandez Jason Heyward & Andrew McCutchen David Wright And Many More! Johnny Sain(d) & Johnny Kucks Fernando Valenzuela & Mike Scioscia Craig Kimbrel & Rafael Furcal And More! Orders Due: Release Date: 24 Boxes Only 90 Case Item Code: All Boxes Individually August 15, 2013 September 11, 2013 Per Case Cases I0028237 Numbered to 2,160 ©2013 TRISTAR Productions, Inc. -

Explaining the Joy in the Text of Jim Bouton's Ball Four: a Study In
Copyright 2019:George D. Gopen 1 Explaining the Joy in the Text of Jim Bouton’s Ball Four: A Study in Analyzing Prose Rhythm by Reader Expectations and Colometrics George D. Gopen Professor Emeritus of the Practice of Rhetoric Duke University Jim Bouton’s Ball Four is clearly a “good read.” It is a “page turner.” We smile, we cackle, we think, we are moved. How does his writing make us do these things? In my work both as an English professor and as a writing consultant to professionals( lawyers, scientists, and academics), I have developed two new techniques for explaining why prose succeeds (or fails) to communicate to readers what the writer was trying to say. I call these techniques the”Reader Expectation Approach to Writing” and “Colometrics.” This essay will explain a bit about them, demonstrating through them how and why Jim Bouton’s book has continued to engage readers for half a century. 2 I. Introduction: A Good Rhetorical Ear Look at the way he invites us in as readers. The opening moment of his Introduction demonstrates not only an awareness of the power of rhetoric, but a wish to engage in it. I’m 30 years old and I have these dreams. (p. xvii-xix) Each of the next 3 paragraphs begins with “I dream”; and then the next paragraph begins with “I dream all these things, I really do.” This is an attempt at “the high style,” in which most of the rest of the book is not written. He apparently felt the opening was a place to be formal, to attempt the uplifting. -

Baseball in Wartime Newsletter No 13 Now Available
Volume 2, Issue 13 Gary Bedingfield’s September 2008 Contact: Baseball in Wartime [email protected] www.baseballinwartime.com Hall of Famers in World War II elcome to the thirteenth edition Name Position Branch of Service Location Years Served of the Baseball in Wartime Luke Appling Shortstop US Army USA 1944-1945 newsletter - a free, monthly W publication dedicated to the Al Barlick Umpire US Coast Guard USA 1943-1945 military service of baseball players during Yogi Berra Catcher US Navy Europe 1944-1945 World War II with a circulation in excess of Willard Brown Outfield US Army Europe 1944-1945 2,000. Nestor Chylak Umpire US Army Europe 1942-1945 This issue focuses on the WWII military service of players who have been elected to Mickey Cochrane Catcher US Navy Pacific 1942-1945 the Baseball Hall of Fame. Of the 286 Hall of Leon Day Pitcher US Army Europe 1944-1945 Fame inductees, 64 saw military service, Bill Dickey Catcher US Navy Pacific 1944-1945 starting with Morgan Bulkeley who served during the Civil War and concluding with Joe DiMaggio Outfield US Army Air Force Pacific 1943-1945 Ernie Banks, Whitey Ford, Eddie Mathews, Larry Doby Outfield US Navy Pacific 1943-1945 Willie Mays and Ted Williams, who all served Bobby Doerr Second Base US Army USA 1944-1945 their nation during the Korean War. Bob Feller Pitcher US Navy Atlantic/Pacific 1941-1945 This newsletter focuses primarily on the 36 Charlie Gehringer Second Base US Navy USA 1942-1945 Hall of Famers who served in the military during World War II. -

Kit Young's Sale #137
Page 1 KIT YOUNG’S SALE #137 BAZOOKA BASEBALL Bazooka cards are among the toughest issues of the 1960’s. These full color cards were featured on boxes of Bazooka bubble gum. We recently picked up a nice grouping – most all cards are clean and really well cut. Many Hall of Famers and Hometown Heroes are offered here. Only one of each available. First time in a few years we’ve offered a big grouping. 1959 Bob Turley 1960 Yogi Berra Yankees 1961 Rocky Colavito Tigers 1963 Don Drysdale Dodgers 1966 Mickey Mantle Yankees 1964 Roberto Clemente Pirates 1965 Juan Marichal Giants Yankees VG 65.00 NR-MT 65.00 EX-MT 39.00 EX-MT 379.00 NR-MT 195.00 EX-MT 60.00 EX-MT 245.00 1959 BAZOOKA 1962 BAZOOKA 1964 BAZOOKA STAMPS Jim Davenport Giants .................................EX-MT $195.00 Mickey Mantle Yankees ...................... EX+/EX-MT $375.00 Juan Marichal Giants ....................................EX-MT $25.00 Roy McMillan Reds.......................................NR-MT 245.00 Johnny Romano Indians ...............................VG-EX 160.00 EX-MT @ $9.50 each: Hinton – Senators, O’Toole – Reds, Duke Snider Dodgers ...................................EX-MT 895.00 Dick Stuart Pirates ....................................VG/VG-EX 25.00 Rollins - Twins Bob Turley Yankees ......................................EX-MT 245.00 1963 BAZOOKA 1965 BAZOOKA 1960 BAZOOKA 2 Bob Rodgers Angels ............................ VG-EX/EX $10.00 2 Larry Jackson Cubs ...................................EX-MT $19.00 4 Hank Aaron Braves..................................NR-MT $195.00 4 Norm Siebern A’s .........................................EX-MT 15.00 3 Chuck Hinton Indians ..................................EX-MT 19.00 8 Yogi Berra Yankees ...........................................VG 65.00 8 Dick Farrell Colt .45s ................... -

1955 Topps Baseball Checklist
1955 Topps Baseball Checklist 1 Dusty Rhodes 2 Ted Williams 3 Art Fowler 4 Al Kaline 5 Jim Gilliam 6 Stan Hack 7 Jim Hegan 8 Hal Smith 9 Bob Miller 10 Bob Keegan 11 Ferris Fain 12 Jake Thies 13 Fred Marsh 14 Jim Finigan 15 Jim Pendleton 16 Roy Sievers 17 Bobby Hofman 18 Russ Kemmerer 19 Billy Herman 20 Andy Carey 21 Alex Grammas 22 Bill Skowron 23 Jack Parks 24 Hal Newhouser 25 Johnny Podres 26 Dick Groat 27 Billy Gardner 28 Ernie Banks 29 Herm Weh Herman Wehmeier on Card 30 Vic Power 31 Warren Spahn 32 Ed McGhee 33 Tom Qualters 34 Wayne Terwilliger 35 Dave Jolly 36 Leo Kiely 37 Joe Cunningham 38 Bob Turley 39 Bill Glynn 40 Don Hoak 41 Chuck Stobbs 42 Windy McCall 43 Harvey Haddix Compliments of BaseballCardBinders.com© 2019 1 44 Corky Valentine 45 Hank Sauer 46 Ted Kazanski 47 Hank Aaron 48 Bob Kennedy 49 JW Porter J.W. Porter on Card 50 Jackie Robinson 51 Jim Hughes 52 Bill Tremel 53 Bill Taylor 54 Lou Limmer 55 Rip Repulski 56 Ray Jablonski 57 Billy O'Dell 58 Jim Rivera 59 Gair Allie 60 Dean Stone 61 Spook Jacobs 62 Thornton Kipper 63 Joe Collins 64 Gus Triandos 65 Ray Boone 66 Ron Jackson 67 Wally Moon 68 Jim Davis 69 Ed Bailey 70 Al Rosen 71 Ruben Gomez 72 Karl Olson 73 Jack Shepard 74 Bob Borkowski 75 Sandy Amoros 76 Howie Pollet 77 Arnie PortoArnold Portocarrero on Card 78 Gordon Jones 79 Danny Schell 80 Bob Grim 81 Gene Conley 82 Chuck Harmon 83 Tom Brewer 84 Camilo Pascual 85 Don Mossi 86 Bill Wilson 87 Frank House 88 Bob Skinner 89 Joe Frazier 90 Karl Spooner Compliments of BaseballCardBinders.com© 2019 2 91 Milt Bolling 92 Don