Coastal Modeling System Draft User Manual
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

SMS User Manual 11.2, Volume 4 Appendix and File Support
SMS User Manual 11.2, Volume 4 Appendix and File Support PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Thu, 13 Mar 2014 18:15:13 CET Contents Articles 7. Appendix 1 FHWA:2010 Webinars 1 SMS 11.2 Dialog Help 2 7.1. Dynamic Model Interface 18 Dynamic Model Interface Schema 18 7.2. File Support 62 XMDF 62 7.2.a. File Formats 64 File Formats 64 2D Mesh Files *.2dm 64 2D Scatter Point Files 92 2D Grid Files 95 ARC/INFO® ASCII Grid Files *.arc 98 ASCII Dataset Files *.dat 99 Binary Dataset Files *.dat 105 Boundary ID Files 110 Boundary XY Files 111 Coastline Files *.cst 112 Color Palette Files *.pal 113 Drogue Files *.pth 113 File Extensions 114 Fleet Wind Files 116 Importing Non-Native SMS Files 117 KMZ Files 118 LandXML Files 120 Lidar Support 121 Map Files 122 MapInfo MID/MIF 123 Material Files *.mat 123 MIKE 21 *.mesh 125 Native SMS Files 126 NOAA HURDAT 128 Quad4 Files 130 Settings Files *.ini 131 Shapefiles 132 SMS Super Files *.sup 133 Tabular Data Files - SHOALS *.pts 134 TIN Files 135 XY Series Files 138 XY Series Editor 140 XYZ Files 141 Generic Vector/Raster Files 142 Import from Web 142 Registering an Image 146 7.2.b. GSDA 149 GSDA 149 GSDA:Digital Elevation 150 GSDA:Hydrography Data 155 GSDA:Imagery 158 GSDA:Meteorologic Data 163 GSDA:Oceanic Data 166 GSDA:Surface Characteristics 169 7.3. Archives 174 Archived Models 174 References Article Sources and Contributors 175 Image Sources, Licenses and Contributors 176 1 7. -
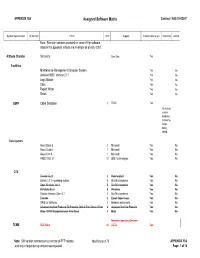
APPENDIX 13A Assigned Software Matrix Contract NAS 10-02007
APPENDIX 13A Assigned Software Matrix Contract NAS 10-02007 System Nomenclature ID Number TITLE QTY Supplier Transferrable to gov Reference Limited Note: Revision numbers provided on some of the software listed in this appendix reflects the inventory as of early 2001. Altitude Chamber Simplicity Gen. Elec. Yes Facilities Maintenance Management Computer System Yes No Andover 9000 Version 2.17 Yes No Logic Master Yes No Citrix Yes No Report Writer Yea No Smart Yes No SSPF Cable Database 1 PGOC Yes No license, custom database. Cables no longer being added. Data Systems Visual Basic 6 2 Microsoft Yes No Visual Suite 6 1 Microsoft Yes No Visual C++ 6 1 Microsoft Yes No PASS 1000 3.7 12 SBS Technologies Yes No CITE Exceed v5.2.1 2 Hummingbird Yes No Solaris 1.0.1 - operating system 8 Sun Microsystems Yes No Open Windows Ver.3 8 Sun Microsystems Yes No VX Works 5.0.2 8 Windriver Yes No Solstice Network Client 3.1 2 Sun Microsystems Yes No Exocode 3 Expert Object Corp. Yes No GPIB for VxWorks 3 National Instruments Yes No Advanced Archival Products SQ Erasable Optical Disk Device Driver 6 Advanced Archival Products Yes No Milan TCP/IP Fastport network Print Serve 3 Milan Yes No Network Computing Devices TCMS PCX Ware 16 (NCD) Yes Note: SW version numbers are current as of RFP release Modification 173 APPENDIX 13A and may change during contract award period. Page: 1 of 16 APPENDIX 13A Assigned Software Matrix Contract NAS 10-02007 System Nomenclature ID Number TITLE QTY Supplier Transferrable to gov Reference Limited (Operations) TCMS 6.0 IRIX -

Computer Applications for Hydrologic Analysis in Mining and Reclamation1
Computer Applications for Hydrologic Analysis in Mining and Reclamation1 by Paul T. Behum, Jr. and Stephen C. Parsons2 Abstract: Since the mid-1980's, the Office of Surface Mining (OSM), in cooperation with State and Tribal coal regulatory and reclamation agencies, has employed a series of technical software tools, under the framework of a program known as the Technical Information Processing System (TIPS). The TIPS program also provides state-of-the-art technical workstations to our State and Tribal partners for use and administration of these software tools. Currently, UNIX-based workstations and software are being replaced by new workstations and servers operating Microsoft Windows NT. This has necessitated a re-evaluation of the technical software to bring legacy UNIX and DOS- based applications to an NT-platform standard. In 1999, a team of State and OSM scientists and engineers evaluated off-the-shelf hydrologic software. The functional areas covered by this review are: (1) aquifer test analyses: software used to evaluate aquifer parameters such as hydraulic conductivity, transmissivity, and storativity; (2) ground-water flow and contaminant transport modeling: application of aquifer parameter data and a U. S. Geological Survey-developed modeling code (MODFLOW) to a conceptual model of subsurface flow and transport conditions for evaluations of ground-water flow and contaminant transport; (3) watershed chemistry and storm runoff analysis: software for studying watershed surface-water quality and stonn/runoff characteristics in both small and large watersheds; ( 4) erosion and sedimentation/channel and impoundment design: supplements to the existing core TIPS software SEDCAD and SURVCADD; and (S) water chemistry analysis: hydrochemical software used for statistical and graphical analysis of both baseline and post-mining data. -

HP-UX 11I V3
QuickSpecs HP-UX 11i v3 Overview QuickSpecs for HP-UX 11i v3 describes the features and functionality delivered by the HP-UX 11i v3 operating environments and related software, plus considerations for a successful, optimized HP-UX 11i deployment. Mission-critical applications are the backbone of every organization's IT, and how well your server environment is equipped to deal with the heavy workload it supports can make or break your business in today's Always-On world. That's why it's important to implement an operating system with the capability to support your organization's massive IT workload that will make the most of your infrastructure. HP-UX 11i v3 comes with a set of features that can provide the best value for your investment. HP-UX 11i v3 is designed to deliver the always-on resiliency, dynamic optimization of resources, investment protection and stability demanded in mission- critical computing. It integrates proven UNIX® functionality with advances in high availability, security, partitioning, workload management, instant-capacity-on-demand and delivers it within the industry's first mission-critical Converged Infrastructure maximizing flexibility while reducing risk and delivering compelling value. HP-UX 11i v3 is: Established as a stable operating environment powering the core of your mission critical applications Providing a proven operating environment delivering the industry's most resilient UNIX platform that ensures your mission- critical applications are always-on and secure without compromise Managed seamlessly within your Converged Infrastructure. Delivers built-in integration of virtualization and management software to optimize IT infrastructure dynamically Features and functionality described in this HP-UX 11i v3 QuickSpecs includes HP-UX 11i v3 March 2013 (Update 12), the latest update release. -

HP Integrity Superdome Servers 16- Processor, 32- Quickspecs Processor, and 64- Processor Systems Overview
HP Integrity Superdome Servers 16- processor, 32- QuickSpecs processor, and 64- processor Systems Overview DA - 11717 Worldwide — Version 31 — June 1, 2006 Page 1 HP Integrity Superdome Servers 16- processor, 32- QuickSpecs processor, and 64- processor Systems Overview At A Glance The latest release of Superdome, HP Integrity Superdome supports the new and improved sx2000 chip set. The Integrity Superdome with the sx2000 chipset supports the Mad9M Itanium 2 processor at initial release. HP Integrity Superdome supports the following processors: sx2000 Itanium 2 1.6-GHz processor sx1000 Itanium 2 1.5 GHz and 1.6 GHz processors HP mx2 processor module based on two Itanium 2 processors HP sx1000 Integrity Superdome supports mixing the Itanium 2 1.5 GHz processor, the Itanium 2 1.6 GHz processor and the HP mx2 processor module in the same system, but on different partitions, as long as they have the same chipset. All cell boards to be mixed in a system must contain the same chipset, sx1000 or sx2000, but not both. HP Integrity Superdome also supports mixing the Itanium 2 1.6 GHz processor, PA 8800 and PA 8900 processors in the same system, but on different partitions, again only with the same chipset, sx1000 or sx2000. Throughout the rest of this document, the term HP sx1000 Integrity Superdome with Itanium 2 1.5 GHz processors, Itanium 2 1.6 GHz processors or mx2 processor modules will be referred to as simply "Superdome sx1000". The HP sx2000 Integrity Superdome with Itanium 2 1.6 GHz processors will be referred to as "Superdome sx2000". -

HPE Systems Insight Manager Overview
QuickSpecs HPE Systems Insight Manager Overview HPE Systems Insight Manager 7.6 Limited Release2 HPE Systems Insight Manager (HPE SIM) is the foundation for the HPE unified server-storage management strategy. HPE SIM is a hardware-level management product that supports multiple operating systems on HPE ProLiant, Integrity and HPE 9000 servers, HPE MSA, EVA, XP arrays, and third-party arrays. Through a single management view of Microsoft® Windows®, VMWare vSphere (ESX/ESXi), HP-UX 11iv2, HP-UX 11iv3, and Red Hat, and SUSE Linux, HPE SIM provides the basic management features of system discovery and identification, single-event view, inventory data collection, and reporting. The core HPE SIM software uses Web Based Enterprise Management (WBEM) to deliver the essential capabilities required to manage all HPE server platforms. HPE SIM can be extended to provide systems management with plug-ins for HPE client, server, storage, power, and printer products. HPE Insight Control and Matrix Operating Environment build on and complement the HPE SIM capabilities with deployment, migration, power and performance management, remote monitoring and control, integrated support for virtualization, infrastructure provisioning and optimization, and continuity of services protection. Plug-in applications for workload management, capacity management, virtual machine (VM) management, and partition management using HPE Integrity Essentials enable you to choose the value-added software that delivers complete lifecycle management for your hardware assets. Most IT organizations understand that ongoing administration and maintenance of existing infrastructure consumes the lion's share of their IT budgets, while hardware and software acquisition costs only account for about 20% of overall expenditures. How can you reduce your IT expenses? By streamlining your processes and reducing complexity.