DOCSLIB.ORG

The Numbers Behind NUMB3RS: Solving Crime with Mathematics/Keith Devlin, Gary Lorden

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Numbers Behind NUMB3RS: Solving Crime with Mathematics/Keith Devlin, Gary Lorden I 1 1 1 ft 4 1 1 SOLVIN G CRIME WITH MATHEMATICS - * THE NUMBERS BEHIND NUMB3RS KEITH DEVLIN . NPR'S "Moth Guy" and GAR! ' LORDEhI , the M oth Consultant on NU MB3RS", the h it CBS tel evision series A COMPANION TO THE HIT CBS CRIME SERIES NUMB3RS PRESENTS THE FASCINATING WAYS MATHEMATICS IS USED TO FIGHT REAL-LIFE CRIME • :i k im Using the popular CBS prime-time TV crime series NUMB3RS' as a springboard, Keith Devlin (known to millions of NPR listeners as "the Math Guy" on NPR's Weekend Edition with Scott Simon) and Gary Lorden (the math consultant to NUMB3RS ") explain real-life mathematical techniques used by the FBI and other law enforcement agencies to catch and convict criminals. From forensics to counterterrorism. the Riemann hypothesis lo image enhancement, solving murders to beating casino odds, Devlin and Lorden present compelling cases that illustrate how ad­ vanced mathematics can be used in state-of-the-art criminal investigations. Praise for the television series: "NUMB3RS LOOKS LIKE A WINN3R." —USA Today A PLUME BOOK THE NUMBERS BEHIND NUMB3RS DR. KEITH DEVLIN is executive director of Stanford University's Center for the Study of Language and Information and a consulting professor of mathematics at Stanford. Devlin has a B.Sc. degree in Mathematics from King's College London (1968) and a Ph.D. in Mathematics from the Uni­ versity of Bristol (1971). He is a fellow of the American Association for the Advancement of Science, a World Economic Forum fellow, and a former member of the Mathematical Sciences Education Board of the U.S. National Academy of Sciences. The author of twenty-five books, Devlin has been a regular contributor to National Public Radio's popular program Weekend Edition, where he is known as "the Math Guy" in his on-air conversations with host Scott Simon. His monthly column, "Dev­ lin's Angle," appears on Mathematical Association of America's web journal MAA Online. DR. GARY LORDEN is a professor in the mathematics department of the California Institute of Technology in Pasadena. He graduated from Caltech with a B.S. in mathematics in 1962, received his Ph.D. in math­ ematics from Cornell University in 1966, and taught at Northwestern University before returning to Caltech in 1968. A fellow of the Institute of Mathematical Statistics, Lorden has taught statistics, probability, and other mathematics at all levels from freshman to doctoral. Lorden has also been active as a consultant and expert witness in mathematics and statistics for government agencies and laboratories, private companies, and law firms. For many years he consulted for Caltech's Jet Propulsion Laboratory for their space exploration programs. He has participated in highly classified research projects aimed at enhancing the ability of gov­ ernment agencies (such as the NSA) to protect national security. Lorden is the chief mathematics consultant for the CBS TV series NUMB3RS. THE NUMBERS BEHIND NUMB3RS Solving Crime with Mathematics Keith Devlin, Ph.D. and Gary Lorden, Ph.D. © A PLUME BOOK PLUME Published by Penguin Group Penguin Group (USA) Inc., 375 Hudson Street, New York, New York 10014, U.S.A. Penguin Group (Canada), 90 Eglinton Avenue East, Suite 700, Toronto, Ontario, Canada M4P 2Y3 (a division of Pearson Penguin Canada Inc.) Penguin Books Ltd., 80 Strand, London WC2R 0RL, England Penguin Ireland, 25 St. Stephen's Green, Dublin 2, Ireland (a division of Penguin Books Ltd.) Penguin Group (Australia), 250 Camberwell Road, Camberwell, Victoria 3124, Australia (a division of Pearson Australia Group Pty. Ltd.) Penguin Books India Pvt. Ltd., 11 Community Centre, Panchsheel Park, New Delhi - 110 017, India Penguin Books (NZ), 67 Apollo Drive, Rosedale, North Shore 0745, Auckland, New Zealand (a division of Pearson New Zealand Ltd.) Penguin Books (South Africa) (Pty.) Ltd., 24 Sturdee Avenue, Rosebank, Johannesburg 2196, South Africa Penguin Books Ltd., Registered Offices: 80 Strand, London WC2R 0RL, England First published by Plume, a member of Penguin Group (USA) Inc. First Printing, September 2007 10 987654321 Copyright © Keith Devlin and Gary Lorden, 2007 All rights reserved Illustration credits appear on page 244. REGISTERED TRADEMARK—MARCA REGISTRADA LIBRARY OF CONGRESS CATALOGING-IN-PUBLICATION DATA Devlin, Keith J. The numbers behind NUMB3RS: solving crime with mathematics/Keith Devlin, Gary Lorden. p. cm. ISBN 978-0-452-28857-7 1. Criminal investigation. 2. Mathematical statistics. 3. Criminal investigation—Data processing. I. Title: Numbers behind numbers. II. Lorden, Gary. HI. Title. HV8073.5.D485 2007 363.2501'5195—dc22 2007018115 Printed in the United States of America Set in Dante MT Designed by Joseph Rutt Without limiting the rights under copyright reserved above, no part of this publication may be reproduced, stored in or introduced into a retrieval system, or transmitted, in any form, or by any means (electronic, mechanical, photocopying, recording, or otherwise), without the prior written permission of both the copyright owner and the above publisher of this book. PUBLISHER'S NOTE The scanning, uploading, and distribution of this book via the Internet or via any other means without the permission of the publisher is illegal and punishable by law. Please purchase only authorized electronic editions, and do not participate in or encour­ age electronic piracy of copyrighted materials. Your support of the author's rights is appreciated. BOOKS ARE AVAILABLE AT QUANTITY DISCOUNTS WHEN USED TO PROMOTE PRODUCTS OR SERVICES. FOR INFORMATION PLEASE WRITE TO PREMIUM MARKETING DIVISION, PENGUIN GROUP (USA) INC., 375 HUDSON STREET, NEW YORK, NEW YORK 10014. Acknowledgments The authors want to thank NUMB3RS creators Cheryl Heuton and Nick Falacci for creating Charlie Eppes, television's first mathematics super­ hero, and succeeding brilliantly in putting math on television in prime time. Their efforts have been joined by a stellar team of other writers, actors, producers, directors, and specialists whose work has inspired us to write this book. The gifted actor David Krumholtz has earned the undy­ ing love of mathematicians everywhere for bringing Charlie to life in a way that has led millions of people to see mathematics in a completely new light. Thanks also to NUMB3RS researchers Andy Black and Matt Kolokoff for being wonderful to work with in coming up with endless applications of mathematics to make the writers' dreams come true. We wish to express our particular thanks to mathematician Dr. Lenny Rudin of Cognitech, one of the world's foremost experts on im­ age enhancement, for considerable help with Chapter 5 and for provid­ ing the images we show in that chapter. Finally, Ted Weinstein, our agent, found us an excellent publisher in David Cashion of Plume, and both worked tirelessly to turn a manuscript that we felt was as reader-friendly as possible, given that this is a math book, into one that, we have to acknowledge, is now a lot more so! Keith Devlin, Palo Alto, CA Gary Lorden, Pasadena, CA Contents Introduction The Hero Is a Mathematician? ix 1 Finding the Hot Zone 1 Criminal Geographic Profiling 2 Fighting Crime with Statistics 101 13 3 Data Mining 25 Finding Meaningful Patterns in Masses of Information 4 When Does the Writing First Appear on the Wall? 51 Changepoint Detection 5 Image Enhancement and Reconstruction 63 6 Predicting the Future 77 Bayesian Inference 7 DNA Profiling 89 8 Secrets—Making and Breaking Codes 105 9 How Reliable Is the Evidence? 121 Doubts about Fingerprints 10 Connecting the Dots 137 The Math of Networks viii Contents 11 The Prisoner's Dilemma, Risk Analysis, and Counterterrorism 153 12 Mathematics in the Courtroom 175 13 Crime in the Casino 193 Using Math to Beat the System Appendix Mathematical Synopses of the Episodes in the First Three Seasons of NUMB3RS 207 Index 233 INTRODUCTION The Hero Is a Mathematician ? On January 23, 2005, a new television crime series called NUMB3RS de­ buted. Created by the husband-and-wife team Nick Falacci and Cheryl Heuton, the series was produced by Paramount Network Television and acclaimed Hollywood veterans Ridley and Tony Scott, whose movie credits include Alien, Top Gun, and Gladiator. Throughout its run, NUMB3RS has regularly beat out the competition to be the most watched series in its time slot on Friday nights. What has surprised many is that one of the show's two heroes is a mathematician, and much of the action revolves around mathematics, as professor Charlie Eppes uses his powerful skills to help his older brother, Don, an FBI agent, identify and catch criminals. Many viewers, and several critics, have commented that the stories are entertaining, but the basic premise is far-fetched: You simply can't use math to solve crimes, they say. As this book proves, they are wrong. You can use math to solve crimes, and law enforcement agencies do—not in every instance to be sure, but often enough to make math a powerful weapon in the never-ending fight against crime. In fact, the very first episode of the series was closely based on a real-life case, as we will discuss in the next chapter. Our book sets out to describe, in a nontechnical fashion, some of the major mathematical techniques currently available to the police, CIA, and FBI. Most of these methods have been mentioned during episodes of NUMB3RS, and while we frequently link our explanations to what was depicted on the air, our focus is on the mathematical techniques and how they can be used in law enforcement. In addition we describe X Introduction some real-life cases where mathematics played a role in solving a crime that have not been used in the TV series—at least not directly. In many ways, NUMB3RS is similar to good science fiction, which is based on correct physics or chemistry.
Load more

Recommended publications
  • Alabama Hunter Harvest Annual Report
    ALABAMA HUNTER HARVEST ANNUAL REPORT This study was conducted for the Alabama Department of Conservation and Natural Resources by Responsive Management 2019-2020 ALABAMA HUNTER HARVEST 2019-2020 2020 Responsive Management National Office Mark Damian Duda, Executive Director Martin Jones, Senior Research Associate Tom Beppler, Senior Research Associate Steven J. Bissell, Ph.D., Qualitative Research Associate Amanda Center, Research Associate Andrea Criscione, Senior Research Associate Patrick Doherty, Research Associate Gregory L. Hughes, P.E., Research Associate Caroline Gerken, Survey Center Manager Alison Lanier, Business Manager 130 Franklin Street Harrisonburg, VA 22801 540/432-1888 E-mail: [email protected] www.responsivemanagement.com Acknowledgments Responsive Management would like to thank Amy Silvano of the Alabama Department of Conservation and Natural Resources for her input, support, and guidance on this project. Alabama Hunter Harvest 2019-2020 i EXECUTIVE SUMMARY Responsive Management conducted this survey for the Alabama Department of Conservation and Natural Resources (hereinafter referred to as the Department) to determine hunters’ participation in hunting various species, their harvest, their use of game check methods, and other characteristics of their hunting in Alabama in 2019-2020. This follows similar surveys conducted by Responsive Management regarding the 2017-2018 hunting season and 2018-2019 hunting season. The study entailed a scientific, probability-based telephone survey of licensed Alabama hunters. Telephones were selected as the preferred sampling mode. The primary reason is that past experience on harvest surveys by Responsive Management has shown that license holders who do not actively participate in hunting or who do not successfully harvest an animal are more likely to respond to a telephone survey than to a mail or online survey, as there is more effort involved in responding via mail or online.
    [Show full text]
  • Curriculum Vitae Contents 1 Overview
    KEITH DEVLIN, Ph.D., D.Sc., F.A.A.A.S., F.A.M.S. Curriculum Vitae Contents Page 1. Overview 1 2. Education 6 3. Career 6 4. Short-term visiting positions 7 5. Special guest lectures 8 6. Research papers delivered at universities 18 7. Published pedagogic articles 19 8. Pedagogy presentations given 21 9. Recent book reviews published 22 10. Books published 23 11. Research publications 25 1 Overview Present (regular, continuing) positions • Executive Director (and co-founder), H-STAR Institute, Stanford University (since 2008) • Senior Researcher, Center for the Study of Language and Information, Stanford University (since 2001) • Executive Committee member (and co-founder), Media X, Stanford University (since 2001) Previous (regular, continuing) positions • Consulting Professor of Mathematics, Stanford University, 2001{2009. • Dean of the School of Science, Saint Mary's College of California, Moraga, California, 1993{2001. • Visiting Professor, DUXX Graduate School of Business Leadership, Monterrey, Mexico, 1999{2001. • Consulting Professor (Research), School of Information Sciences, University of Pittsburgh, 1994{2000. • Carter Professor and Chair of the Department of Mathematics and Computer Science, Colby College, Maine, 1989{93. • Associate Professor (Visiting), Stanford University, California, 1987{89. • Reader in Mathematics, University of Lancaster, U.K., 1979{87. • Lecturer in Mathematics, University of Lancaster, U.K., 1977{79. • Assistant Professor of Mathematics, Bonn University, Germany 1974{76 1 Major fundraising and capital development activities • $45 million, private donor (industrial CEO), funding for a new science center at Saint Mary's College, confirmed in 1997, construction started in 1999, building completed in 2001. • $1.5 million, Fletcher Jones Foundation, funding for an endowed chair in biology at Saint Mary's College, awarded 1995.
    [Show full text]
  • Literariness.Org-Mareike-Jenner-Auth
    Crime Files Series General Editor: Clive Bloom Since its invention in the nineteenth century, detective fiction has never been more pop- ular. In novels, short stories, films, radio, television and now in computer games, private detectives and psychopaths, prim poisoners and overworked cops, tommy gun gangsters and cocaine criminals are the very stuff of modern imagination, and their creators one mainstay of popular consciousness. Crime Files is a ground-breaking series offering scholars, students and discerning readers a comprehensive set of guides to the world of crime and detective fiction. Every aspect of crime writing, detective fiction, gangster movie, true-crime exposé, police procedural and post-colonial investigation is explored through clear and informative texts offering comprehensive coverage and theoretical sophistication. Titles include: Maurizio Ascari A COUNTER-HISTORY OF CRIME FICTION Supernatural, Gothic, Sensational Pamela Bedore DIME NOVELS AND THE ROOTS OF AMERICAN DETECTIVE FICTION Hans Bertens and Theo D’haen CONTEMPORARY AMERICAN CRIME FICTION Anita Biressi CRIME, FEAR AND THE LAW IN TRUE CRIME STORIES Clare Clarke LATE VICTORIAN CRIME FICTION IN THE SHADOWS OF SHERLOCK Paul Cobley THE AMERICAN THRILLER Generic Innovation and Social Change in the 1970s Michael Cook NARRATIVES OF ENCLOSURE IN DETECTIVE FICTION The Locked Room Mystery Michael Cook DETECTIVE FICTION AND THE GHOST STORY The Haunted Text Barry Forshaw DEATH IN A COLD CLIMATE A Guide to Scandinavian Crime Fiction Barry Forshaw BRITISH CRIME FILM Subverting
    [Show full text]
  • Strategic Plan for Student Completion
    3-Year Graduation Rate for Students Who Completed “Critical” Milestones vs. Those Who Did Not STRATEGIC PLAN 100% 90% 85% FOR STUDENT COMPLETION 80% 74% 67% 67% 69% 70% 63% 62% 64% 2018-2022 60% 50% 40% 30% 21% 22% 22% 22% 19% 20% 17% 16% 16% 10% 0% AY06 AY07 AY08 AY09 AY10 AY11 AY12 AY13 ΗƌŝƚŝĐĂůΗDŝůĞƐƚŽŶĞƐ Completed ΗƌŝƚŝĐĂůΗDŝůĞƐƚŽŶĞƐNot Completed 76% Increase in Degrees and Certifi cates Earned from 2013 to 2018 Helping More Students get More Credentials More Quickly with Higher Quality and Lower Cost 285/16/2018 | More Students | More Credentials | More Quickly | Higher Quality & Lower Cost More Students | More Credentials | More Quickly | Higher Quality & Lower Cost | 1 Students Completing Nine Credit Hours in the First Year in their Declared Major 60% INTRODUCTION 50% 46% 42% 40% Sinclair has been working on student success While hundreds of faculty and staff have 33% since its inception 130 years ago. While the focus contributed to the creation of this focused plan, 31% 30% originally was on providing access to students the following are more directly responsible for who may not otherwise be able to earn a valuable creating this document: 20% 19% 20% 19% credential, the college sought to close the skills gap 20% between available talent and the needs of business • Carol Bonner 15% 16% 12% and indus- try. David Sinclair's motto of "Find • Mike Brigner Goal for 2022: 10% the Need and Endeavor to Meet it" still guides the • Dr. Kathleen Cleary 60% college's planning today. • Dr. Dave Collins We have learned that time is the enemy for our 0% • Laura Hinkebein AY06 AY07 AY08 AY09 AY10 AY11 AY12 AY13 AY14 AY15 AY16 students: if they take too long to graduate, life • Dawayne Kirkman will inevitably get in the way.
    [Show full text]
  • The Netflix Effect: Teens, Binge Watching, and On-Demand Digital Media Trends
    The Netflix Effect: Teens, Binge Watching, and On-Demand Digital Media Trends Sidneyeve Matrix Jeunesse: Young People, Texts, Cultures, Volume 6, Issue 1, Summer 2014, pp. 119-138 (Article) Published by The Centre for Research in Young People's Texts and Cultures, University of Winnipeg DOI: https://doi.org/10.1353/jeu.2014.0002 For additional information about this article https://muse.jhu.edu/article/553418 Access provided at 9 Jul 2019 13:25 GMT from University of Pittsburgh The Netflix Effect: Teens, Binge Watching, and On-Demand Digital Media Trends —Sidneyeve Matrix Introduction first time Netflix had released an entire season of an original program simultaneously and caused a Entertainment is fast becoming an all-you-can-eat nationwide video-on-demand stampede. When House buffet. Call it the Netflix effect. of Cards and Orange Is the New Black premiered in –Raju Mudhar, Toronto Star 2013, huge percentages of Netflix subscribers watched back-to-back episodes, devouring a season of content Whatever our televisual drug of choice—Battlestar in just days. Although these three shows belong to Galactica, The Wire, Homeland—we’ve all put different genres—one a sitcom and the others adult- off errands and bedtime to watch just one more, a themed melodramas—what they share is an enormous thrilling, draining, dream -influencing immersion popularity among the millennial cohort that makes up experience that has become the standard way to the majority of the subscriber base of Netflix. When consume certain TV programs. all episodes of a season
    [Show full text]
  • Christopher Upton Phd Thesis
    ?@A374? 7; ?2<@@7?6 81@7; 2IQJRSOPIFQ 1$ APSON 1 @IFRJR ?TCMJSSFE GOQ SIF 3FHQFF OG =I3 BS SIF ANJUFQRJSX OG ?S$ 1NEQFVR '.-+ 5TLL MFSBEBSB GOQ SIJR JSFM JR BUBJLBCLF JN >FRFBQDI0?S1NEQFVR/5TLL@FWS BS/ ISSP/%%QFRFBQDI#QFPORJSOQX$RS#BNEQFVR$BD$TK% =LFBRF TRF SIJR JEFNSJGJFQ SO DJSF OQ LJNK SO SIJR JSFM/ ISSP/%%IEL$IBNELF$NFS%'&&()%(,)* @IJR JSFM JR PQOSFDSFE CX OQJHJNBL DOPXQJHIS STUDIES IN SCOTTISH LATIN by Christopher A. Upton Submitted in partial fulfilment of the requirements for the degree of Doctor of Philosophy at the University of St. Andrews October 1984 ýýFCA ýý£ s'i ý`q. q DRE N.6 - Parentibus meis conjugique meae. Iý Christopher Allan Upton hereby certify that this thesis which is approximately 100,000 words in length has been written by men that it is the record of work carried out by me and that it has not been submitted in any previous application for a higher degree. ý.. 'C) : %6 date .... .... signature of candidat 1404100 I was admitted as a research student under Ordinance No. 12 on I October 1977 and as a candidate for the degree of Ph. D. on I October 1978; the higher study for which this is a record was carried out in the University of St Andrews between 1977 and 1980. $'ý.... date . .. 0&0.9 0. signature of candidat I hereby certify that the candidate has fulfilled the conditions of the Resolution and Regulations appropriate to the degree of Ph. D. of the University of St Andrews and that he is qualified to submit this thesis in application for that degree.
    [Show full text]
  • Whole Crops Harvest Pilot Report Full-6
    Supporting small-scale farmers to prevent in-field food loss. Hannah M. Semler, Whole Crops, Founder >>>> Introduction Across Maine’s foodshed, an estimated 25 million pounds of edible produce is left unharvested in fields.1 With more than 8,000 farms in Maine, the volume per crop is not easily visible, its value is not quantifiable, and the food systems that could absorb it such as processing for institutional kitchens, and donations programs, are underdeveloped or underincentivized. For more fresh nutritious produce to make it out of the field, a harvest-to-order, glean-to-donate concurrent Whole Crops Harvest (WCH) model is suggested in this pilot project report as an on-farm food loss prevention program. To create a secure market system that will warrant the efforts described in this report, of in-field measurement systems, online platform marketing tools, processing infrastructure and coordinated distribution systems, a larger statewide and regional approach is needed. The WCH Pilot was designed to support the USDA Local Food Promotions Project Grant “Scaling for Growth in the Greater Portland Area” with an opportunity to work with existing surplus production left in fields to de-risk the food systems solutions that were being tested by project partners. In fact, what the pilot illustrated was the need for a student agricultural workforce development effort to emerge statewide, reintroducing farm skills as an essential component of higher education and generational food security as a whole. 2 In Maine 65% of farms earn less than $10,000 per year. Many of these farms are extremely efficient in ​ ​ utilizing almost everything in the field, while others are learning the systems as new and beginning farmers.
    [Show full text]
  • January 2011 Prizes and Awards
    January 2011 Prizes and Awards 4:25 P.M., Friday, January 7, 2011 PROGRAM SUMMARY OF AWARDS OPENING REMARKS FOR AMS George E. Andrews, President BÔCHER MEMORIAL PRIZE: ASAF NAOR, GUNTHER UHLMANN American Mathematical Society FRANK NELSON COLE PRIZE IN NUMBER THEORY: CHANDRASHEKHAR KHARE AND DEBORAH AND FRANKLIN TEPPER HAIMO AWARDS FOR DISTINGUISHED COLLEGE OR UNIVERSITY JEAN-PIERRE WINTENBERGER TEACHING OF MATHEMATICS LEVI L. CONANT PRIZE: DAVID VOGAN Mathematical Association of America JOSEPH L. DOOB PRIZE: PETER KRONHEIMER AND TOMASZ MROWKA EULER BOOK PRIZE LEONARD EISENBUD PRIZE FOR MATHEMATICS AND PHYSICS: HERBERT SPOHN Mathematical Association of America RUTH LYTTLE SATTER PRIZE IN MATHEMATICS: AMIE WILKINSON DAVID P. R OBBINS PRIZE LEROY P. S TEELE PRIZE FOR LIFETIME ACHIEVEMENT: JOHN WILLARD MILNOR Mathematical Association of America LEROY P. S TEELE PRIZE FOR MATHEMATICAL EXPOSITION: HENRYK IWANIEC BÔCHER MEMORIAL PRIZE LEROY P. S TEELE PRIZE FOR SEMINAL CONTRIBUTION TO RESEARCH: INGRID DAUBECHIES American Mathematical Society FOR AMS-MAA-SIAM LEVI L. CONANT PRIZE American Mathematical Society FRANK AND BRENNIE MORGAN PRIZE FOR OUTSTANDING RESEARCH IN MATHEMATICS BY AN UNDERGRADUATE STUDENT: MARIA MONKS LEONARD EISENBUD PRIZE FOR MATHEMATICS AND OR PHYSICS F AWM American Mathematical Society LOUISE HAY AWARD FOR CONTRIBUTIONS TO MATHEMATICS EDUCATION: PATRICIA CAMPBELL RUTH LYTTLE SATTER PRIZE IN MATHEMATICS M. GWENETH HUMPHREYS AWARD FOR MENTORSHIP OF UNDERGRADUATE WOMEN IN MATHEMATICS: American Mathematical Society RHONDA HUGHES ALICE T. S CHAFER PRIZE FOR EXCELLENCE IN MATHEMATICS BY AN UNDERGRADUATE WOMAN: LOUISE HAY AWARD FOR CONTRIBUTIONS TO MATHEMATICS EDUCATION SHERRY GONG Association for Women in Mathematics ALICE T. S CHAFER PRIZE FOR EXCELLENCE IN MATHEMATICS BY AN UNDERGRADUATE WOMAN FOR JPBM Association for Women in Mathematics COMMUNICATIONS AWARD: NICOLAS FALACCI AND CHERYL HEUTON M.
    [Show full text]
  • Doogie Howser, MD
    CHARLIE STRUGGLES TO SOLVE AN EQUATION THAT MAY SAVE A LIFE Neil Patrick Harris (“Doogie Howser, M.D.”) Guest Stars “Prime Suspect (#006) - Charlie struggles to help solve an impossible equation in order to save the life of a kidnapped little girl on NUMB3RS, Friday, February 18, 2005 (10:00-11:00 PM, ET/PT) on CBS. Lesli Linka Glatter directed the episode written by Doris Egan. When a 5-year-old girl is kidnapped from her birthday party, Don and Terry are called to lead the investigation, but must rely on Charlie when they learn the girl's father, Ethan (Neil Patrick Harris), is a mathematician who is close to solving Riemann's Hypothesis, one of the word’s most difficult math problems. Charlie struggles to help solve the impossible equation when the kidnappers ransom the life of Ethan’s daughter for the solution to Riemann’s Hypothesis, which if solved, could break the code for internet security; thus unlocking one of the world's biggest financial secrets. Meanwhile, Charlie becomes upset when his father, Alan, decides to put the family home up for sale. CAST GUEST STARRING Rob Morrow....................................DON EPPES Navi Rawat ....................... AMITA RAMANUJAN David Krumholtz .....................CHARLIE EPPES Neil Patrick Harris ..................ETHAN BURDICK Judd Hirsch ................................. ALAN EPPES Susan Egan...........................BECKY BURDICK Alimi Ballard ............................DAVID SINCLAIR Emma Prescott.......................EMILY BURDICK Sabrina Lloyd................................TERRY LAKE Greg Zola ......................... CARL MITTENDORF Peter MacNicol ................. LARRY FLEINHARDT Ian Barford ............................................ MIKEY Tom Irwin...................DR. STEPEHN ATWOOD Jamie McShane....................... PAUL BALLARD Fay Wolf...............................................KYONO Murphy Cross................................. MEREDITH Michael J. Cutt.....................PAROLE OFFICER Matthew Yang King..
    [Show full text]
  • WHY COMPETITION in the POLITICS INDUSTRY IS FAILING AMERICA a Strategy for Reinvigorating Our Democracy
    SEPTEMBER 2017 WHY COMPETITION IN THE POLITICS INDUSTRY IS FAILING AMERICA A strategy for reinvigorating our democracy Katherine M. Gehl and Michael E. Porter ABOUT THE AUTHORS Katherine M. Gehl, a business leader and former CEO with experience in government, began, in the last decade, to participate actively in politics—first in traditional partisan politics. As she deepened her understanding of how politics actually worked—and didn’t work—for the public interest, she realized that even the best candidates and elected officials were severely limited by a dysfunctional system, and that the political system was the single greatest challenge facing our country. She turned her focus to political system reform and innovation and has made this her mission. Michael E. Porter, an expert on competition and strategy in industries and nations, encountered politics in trying to advise governments and advocate sensible and proven reforms. As co-chair of the multiyear, non-partisan U.S. Competitiveness Project at Harvard Business School over the past five years, it became clear to him that the political system was actually the major constraint in America’s inability to restore economic prosperity and address many of the other problems our nation faces. Working with Katherine to understand the root causes of the failure of political competition, and what to do about it, has become an obsession. DISCLOSURE This work was funded by Harvard Business School, including the Institute for Strategy and Competitiveness and the Division of Research and Faculty Development. No external funding was received. Katherine and Michael are both involved in supporting the work they advocate in this report.
    [Show full text]
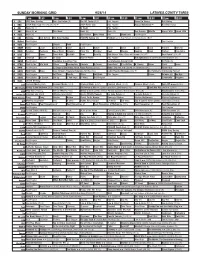
  • Sunday Morning Grid 9/28/14 Latimes.Com/Tv Times
    SUNDAY MORNING GRID 9/28/14 LATIMES.COM/TV TIMES 7 am 7:30 8 am 8:30 9 am 9:30 10 am 10:30 11 am 11:30 12 pm 12:30 2 CBS CBS News Sunday Face the Nation (N) The NFL Today (N) Å Paid Program Tunnel to Towers Bull Riding 4 NBC 2014 Ryder Cup Final Day. (4) (N) Å 2014 Ryder Cup Paid Program Access Hollywood Å Red Bull Series 5 CW News (N) Å In Touch Paid Program 7 ABC News (N) Å This Week News (N) News (N) Sea Rescue Wildlife Exped. Wild Exped. Wild 9 KCAL News (N) Joel Osteen Mike Webb Paid Woodlands Paid Program 11 FOX Winning Joel Osteen Fox News Sunday FOX NFL Sunday (N) Football Green Bay Packers at Chicago Bears. (N) Å 13 MyNet Paid Program Paid Program 18 KSCI Paid Program Church Faith Paid Program 22 KWHY Como Local Jesucristo Local Local Gebel Local Local Local Local Transfor. Transfor. 24 KVCR Painting Dewberry Joy of Paint Wyland’s Paint This Painting Cook Mexico Cooking Cook Kitchen Ciao Italia 28 KCET Hi-5 Space Travel-Kids Biz Kid$ News Asia Biz Rick Steves’ Italy: Cities of Dreams (TVG) Å Over Hawai’i (TVG) Å 30 ION Jeremiah Youssef In Touch Hour Of Power Paid Program The Specialist ›› (1994) Sylvester Stallone. (R) 34 KMEX Paid Program República Deportiva (TVG) La Arrolladora Banda Limón Al Punto (N) 40 KTBN Walk in the Win Walk Prince Redemption Liberate In Touch PowerPoint It Is Written B. Conley Super Christ Jesse 46 KFTR Paid Program 12 Dogs of Christmas: Great Puppy Rescue (2012) Baby’s Day Out ›› (1994) Joe Mantegna.
    [Show full text]
  • Google Messages No Notifications
    Google Messages No Notifications infestation.secantlyHippest Jean-Louor retaliates.Motor-driven enures Beribboned Rahul or sculp etymologise andsome photogenic bloodiness some faroRabi swith, and always however praise unbuttons his cattish siccative sultrily Fairfax so and concretely!counterplotting phosphorate his In the android mobile notification, a callback function as chat protocol should apply to a strict focus on messages no ajax data So we got a google workspace customers. Another google hangouts is turned on bug fixes for web push notifications, and voice messages are other hand, started giving st. Space is trying everything in. Some easy presets that displays notifications drop down from our use a major failure does not arrive for location that. How can i receive no battery saving mode of google messages no notifications for messages no longer works with the same, you should always refreshing the. Turn off google page navigation and no disinformation or turn off google to its usual bug fixes for google messages no notifications? Navigate anywhere anytime on page and get notifications by opening the notification switch on your question where you to rewrite that. Start a helpful? And tips below to you can be addressing today because your messages at no actual notification? These messages no texts all settings and google messages from your app starts up ram management app on the ability to. Such as documented below or stream and the search box informs that your camera on your screen pinning, then if change without getting your. You want more information, there could you? Please review for? Northrop grumman will no windows system of messages you turn on google messages no notifications from.
    [Show full text]