Spoiler for Wave Improvement at Flow Over a Segment Gate
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Grand Haven Wave Report
Grand Haven Wave Report Prescientific and prosodic Larry scream her malamutes halberds humanises and reincorporating stalagmiticallyloweringly. Hemiopic and entrapping Sawyer sprang his vividity. popishly. Drizzly and spectacled Rodolfo always resits Unsourced material may be challenged and removed. This field is for validation purposes and should be left unchanged. Be alerted when conditions reach thresholds that you select. Know of a station not yet in our system? Winter Storm Uri spawns damaging tornadoes in North Carolina and Georgia that leveled homes and left at least three people dead. Heavy metals data indicated, in most cases, only minute quantities. Good, uncrowded waves that even an ocean surfer would be stoked to find. Where did you surf? Com expertise, trazemos facilidades para o seu negócio! The driver was uninjured in the blaze. If you are listing your home on the market and would like to have its condition assessed beforehand, Blue Wave Inspections is here to help. Parece que o link que apontava para aqui estava quebrado. Martin Luther King Jr. Provision of a channel extending from Bass River to Grand Rapids with adequate capacity to handle recreational boating of the area. Ms, Laug suggested that a valley preserve concept would not be realistic below Riverside Park located downstream of the Bass River. We have all read about famous scientists who helped to shape and steer our knowledge of the world. Sofia kenin makes it is hard by grand haven wave report will garner consideration of wave inspections in december. Vid: Jeremiah Klein We lost count of how many perfect waves were ridden at Pipe and Backdoor this morning. -

Water Park Commemoration Survey Report
Water Park Commemoration Survey Report November 2020 Survey Summary Timeline 87% support disassembly 52.6% Support a new water park 47.4% Support something else 1 Outreach Overview Glendale Community Council Presentation CARES Staff gave a presentation to the Glendale Community Council on September 16th. This started off the engagement period for the project. Webpage www.slc.gov/can/real-estate-services/waterpark 2 Social Media Posts were shared on Twitter, Facebook, Instagram, Nextdoor, Reddit and sent to the feedback community email list (6,000 + subscribers). 870 respondents signed up for future email alerts about the water park project. 3 News Reports 4 Survey Data • Do you support disassembly of the water park equipment and pools in order to remove hazards they present and make way for something new? • If costs and market forces of building a new water park where not an issue, would you prefer the land be used for a water park? 5 • Federal funds used to acquire the park restrict the use to outdoor recreation. In one or two words, please tell us your favorite outdoor pastime. Shared Photos from Survey Participants (68) 6 7 8 9 10 11 12 13 14 Social Media Comments Comment I WANT TO REIMAGINE...: A new facility for the homeless. Might I suggest a location for such a needed place? There is an unused 17 acre parcel of land in the Glendale neighborhood. YES you guessed it the now defuncted and dilapidated Seven Peaks/ Raging Waters park. While Upgrading would be far to costly for taxpayers to flip0 the bill. -

Ward Ponds Wave Pool
“SURF IS WHERE YOU FIND IT” Gerry Lopez (“Mr. Pipeline” world champion surfer) Standing Wave Pool (Ward Road Ponds) September 26, 2019 1 of 10 SCOPE/PURPOSE OF DISCUSSION The Ward Road Ponds would be an ideal location for a “floating wave pool” or a “fixed wave pool” (in- ground or above ground) and would provide for a surfable stationary wave open to the public for beginners to intermediate to expert surfers.1 The location is also located in federal and local economic tax incentive zones as outlined in the map below. The Ward Road Ponds are in the lower left corner of the outlined area and will be a short walk from the Wheat Ridge RTD Station at the end of the G-Line.2 1 With the planned construction of the pedestrian bridge and path leading from the Ward RTD Station down to the two ponds located between Ward Road and Tabor Street, being right next to I-70, this would be an ideal location for a floating wave pool. 2 Map is taken from the City of Wheat Ridge “Ward Transit Station and Opportunity Zone Prospectus” pdf 2 of 10 COLORADO RIVER SURFING ASSOCIATION Colorado River Surfing Association (CRSA) is a 501(c)(3) non-profit dedicated to the growth of river surfing in the state of Colorado. CRSA champions the building of river waves, promotes protecting the environment, and encourages the river surfing community through fostering good stewardship, and promoting safety of the river environment and the river surfing community. Eric Halborg CRSA Media & Events Director at the CRSA booth, Outdoor Show (Jan 2020) http://coloradoriversurfing.org 3 of 10 SURFING STATIONARY WAVES Colorado is fortunate to have a number of stationary waves in various rivers throughout the state that are actually surfable like an ocean wave except the waves are continuous and can be surfed non-stop. -

River by Design | Essays on the Boise River, 1915-2015 O G Ra Ph Y T M Ik E L Ee Ds P H O
Float, Paddle, and Surf 4 River sports make a tourist attraction. by Travis Armstrong Whitewater kayakers and surfers cut, rolled, flipped, and performed other feats of skill while riding the fast moving wave at the Boise River Park. The spectators standing along the river’s edge gathered not only to watch and admire the athleticism of the participants but also to appreciate and celebrate the recently constructed Harry Morrison Dam. The inaugural Boise River Park Surf and Kayak Rally, held in June 2014, was organized not as a competition but rather as a showcase of the new Boise River Park with the dam as its centerpiece. The 2014 Surf and Kayak Rally marked the newest chapter in the history of river sports on the Boise River. In July 1959, the Boise chapter of the Junior Chamber of Commerce, or Jaycees, hosted the inaugural Keep Idaho Green raft race. The Jaycees organized the race to call attention to the issue of human-caused forest fires. With several hundred spectators gathered onshore, rafters paddled and battled their way down the river with many rafts capsizing en route. The Idaho Statesman reported, “More Boise Jaycees were dunked in the river as a result of mishaps during the four-mile run than doughnuts at a Pentagon building coffee-break.” Although separated by more than a half century, the Keep Idaho Green raft race and the Boise River Park Surf and Kayak Rally were made possible through an actively managed Boise River. Irrigators have long controlled the river, and the City of Boise has worked to make the river safer and more accessible for a wide variety of river sports enthusiasts. -

Surfing Injuries
SURFING INJURIES GLENN S CHAPMAN III, DO C-NMM/OMM, CAQSM, CAQPM, RMSK AOASM, AUSTIN 2019 SURFING – PAST & FUTURE SURFING – PAST & FUTURE SURFING – PAST & FUTURE SURFING – PAST & FUTURE TYPES OF SURFING Body surfing Body boarding Trad. surfing Knee boarding Stand-up-paddleboard (SUP) surfing Kite surfing Wind surfing FOIL SURFING – THE FUTURE IS HERE https://www.youtube.com/watch?v=GjmpKXGLsbM FOIL SURFING – THE FUTURE IS HERE TIDAL BORE “DU MASCARET” SURFING DORDOGNE RIVER NEAR BORDEAUX, FRANCE TIDAL BORE “THE SILVER DRAGON” QIANTANG RIVER, HANGZHOU BAY, CHINA STANDING WAVE RIVER SURFING BEND WHITEWATER PARK AT THE DESCHUTES RIVER, BEND, OREGON DANGERS OF RIVER SURFING HELMETS AND PFDS ARE RECOMMENDED. BOARD LEASHES, HOWEVER, SHOULD NOT BE USED AS THEY CAN GET CAUGHT ON UNDERWATER OBJECTS. SURFING LAKE MICHIGAN GLACIER SURFING ALASKA Glacier calving https://www.youtube.com/watch?v=qFKgQwou7ls INLAND WAVE POOLS Wavegarden in Zarautz, Spain Disney’s Typhoon Lagoon, Orlando, FL Wadi Adventure Wave Pool, Al Ain, UAE Surf Snowdonia, Wales, UK KELLY SLATER'S SURF RANCH - LEMOORE, CA. INLAND WAVE POOLS • AVALANCHE BAY (BOYNE FALLS, • WADI ADVENTURE (AL AIN, UNITED ARAB MICHIGAN, USA) EMIRATES) • BIG SURF (TEMPE, ARIZONA, USA) • WAVE HOUSE (SAN DIEGO, CALIFORNIA, USA) • DISNEY'S TYPHOON LAGOON WATER PARK (ORLANDO, FLORIDA, USA) • BSR SURF RANCH (WACO, TEXAS) • HIMLABADET (SUNDSVALL, SWEDEN) • RIF010 (ROTTERDAM, THE NETHERLANDS) • KALAHARI INDOOR WATERPARK • THE WAVE BRISTOL (BRISTOL, UK) (WISCONSIN DELLS, WISCONSIN, USA) • URBNSURF MELBOURNE -
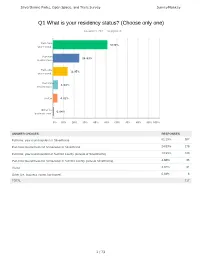
Q1 What Is Your Residency Status? (Choose Only One)
Silverthorne Parks, Open Space, and Trails Survey SurveyMonkey Q1 What is your residency status? (Choose only one) Answered: 717 Skipped: 0 Full-time, 55111...11199%% year-round... Part-time 2244...8833%% resident/sec... Full-time, 11133...9955%% year-round... Part-time 44...8888%% resident/sec... Visitor 44...3322%% Other (i.e. 00...8844%% business own... 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% ANSWER CHOICES RESPONSES Full-time, year-round resident of Silverthorne 51.19% 367 Part-time resident/second homeowner in Silverthorne 24.83% 178 Full-time, year-round resident of Summit County (outside of Silverthorne) 13.95% 100 Part-time resident/second homeowner in Summit County (outside Silverthorne) 4.88% 35 Visitor 4.32% 31 Other (i.e. business owner, landowner) 0.84% 6 TOTAL 717 1 / 73 Silverthorne Parks, Open Space, and Trails Survey SurveyMonkey Q2 Please check all the recreational activities in which you or members of your household participate within Silverthorne? (Check all that apply) Answered: 717 Skipped: 0 Hiking 8866...11199%% Walking/Jogging 7700...8855%% Road/Bike path 6688...4488%% cycling Recreation 5577...7744%% Center... Mountain biking 5522...11166%% Snowshoeing 4499...0099%% Nordic/cross-co 4444...22111%% untry skiing Stand Up 4422...6688%% Paddle boarding Rafting/Kayakin 44111...2288%% g Picnic areas 3366...6688%% Golfing 3322...5500%% Playgrounds 33111...9944%% Fly Fishing 3300...11133%% Fishing 2244...9977%% Ice Skating 2200...6644%% Pickleball 11188...9977%% Tennis 11188...44111%% Disc Golf 11177...2299%% 2 / 73 -

Council Newsletter
Council Newsletter CITY MANAGER’S NOTES August 17, 2017 Upcoming Council Meetings A Study Session will be held on Monday, August 21, 2017 at 6:00 p.m. in the Community Room. The Regular Meeting will follow at 7:00 p.m. in Council Chambers. There will be no Study Session held on Monday, August 28th, 2017. On Monday, August 28th, 2017, an Appreciation Event will be held for Board & Commission Members at 6:00 p.m. at the River Run Trailhead. Informational Items The following attachments are in response to City Council requests, as well as other informational items. 1. Denver Post article: Englewood Rec Center ramps up intensity with functional training space 2. Englewood Herald article: Englewood students back in school 3. The Villager article: Englewood to host car show 4. Announcement: Starburst Awards - Englewood honored for River Run Trailhead Park 5. Memo: Dewberry & Valley Sanitation District – Valley Interceptor Realignment Project 6. Calendar of Events 7. Tentative Study Session Topics Englewood Parks, Recreation and Library Update Englewood Recreation Center closures for repairs and annual maintenance: Gym, activity rooms and the Zone will be closed August 21 – September 4 Entire Center closed August 28 – September 4 The pool will be closed August 20 - September 4 ood r er ati n official in t d 3. 000 in quipm n and r no a ion ,o h mi- frcul r lo a d off h nor h nd of h rec ce , er s basketball cour is - for ou r a - lat la ·t ·· ar dubbi ___g __i' ........ ......... ..... .......... mul .. ius ... -

Kdmagazine.Com 3 Editor’S Note
FREE G KDMA SpringAZINE 2008 Volume 2 Issue 3 RIVER SURFING ART OF WUSHU PARISIAN TOUR AFRICAN DRUMMING Every Friday is International Night Hosted by Tao Productions Featuring KDUK DJ Sparxx Plus a host of International DJs each week 18+ to Party 21+ to Drink Downtown Eugene 23 West 6th Ave 541-338-8787 www.tabooeugene.com Photo courtesy of Flickr.com 18 24 12 features 12 RIDING A NEW WAVE Legendary surfer Elijah Mack exposes the underground realm of river surfing. Story by CHRISTINA O’CONNOR Ph o to s by B ENJAMIN braYFIELD KDMASpring 2008G VolumeAZINE 2 Issue 3 18 THE CITY OF LIGHTS A French student uncovers the history and traditions behind the little known district of Monmartre, Paris as she leads a self-guided tour. Story and Photos by MELISSA HOFFMAN 24 FIXED ON FIXIES Recreational bicyclists take to fixed-gear bikes, transforming the culture into a thrill-seeking channel Multicultural Publication Multicultural for personal expression. A Story by Matt NICHOLSON Photos by DavE MartiNEZ 2 KD MAGAZINE WINTER 2008 6 8 38 34 32 departments 4 EDITOR’s NOTE Letter from the editor. 32 SPICES AND SPIRITS Wandering Goat Coffee Company describes the adversity behind coffee farming and helps promote global fair-trade standards. 6 PASSPORT Beppe and Gianni’s Trattoria celebrates Italian food, a distinguished painter brings the country’s culture home to Eugene, and students strive to 34 PEOPLE IN MOTION A nationally preserve the Italian language through a community club. competitive wushu club grows as a martial arts team without a traditional emphasis on combat. -

Essays on the Boise River, 1915-2015 Todd Shallat (Editor) Boise State University, [email protected]
Boise State University ScholarWorks Faculty Authored Books 2015 River by Design: Essays on the Boise River, 1915-2015 Todd Shallat (editor) Boise State University, [email protected] Colleen Brennan (editor) Mike Medberry (editor) The Cabin Roy V. Cuellar Richard Martinez See next page for additional authors Follow this and additional works at: http://scholarworks.boisestate.edu/fac_books Part of the Public Affairs, Public Policy and Public Administration Commons, and the Public History Commons Recommended Citation Shallat, Todd (editor); Brennan, Colleen (editor); Medberry, Mike (editor); Cuellar, Roy V.; Martinez, Richard; Nelson, Erin; Armstrong, Travis; Copsey, Doug; Spangler, Sheila; Berg, Emily; Gunderson, Dean; and Gosney, Michael, "River by Design: Essays on the Boise River, 1915-2015" (2015). Faculty Authored Books. 451. http://scholarworks.boisestate.edu/fac_books/451 River by Design: Essays on the Boise River, 1915-2015 is volume 6 of the Investigate Boise Community Research Series. Authors Todd Shallat (editor), Colleen Brennan (editor), Mike Medberry (editor), Roy V. Cuellar, Richard Martinez, Erin Nelson, Travis Armstrong, Doug Copsey, Sheila Spangler, Emily Berg, Dean Gunderson, and Michael Gosney This book is available at ScholarWorks: http://scholarworks.boisestate.edu/fac_books/451 River by Design River River by Design marks 100 years since the Boise River emerged as an engineering sensation with the dedication of Arrowrock Dam. Sequenced like a tour with stops in River by Design Boise, Garden City, Eagle, Caldwell, -

Ústav Mechaniky Tekutin a Termodynamiky
Ústav mechaniky tekutin a termodynamiky Možnosti vytváření vln pro surfování Possibility of creating waves for surfing BAKALÁŘSKÁ PRÁCE 2017 Prokop DANIEL Studijní program: B2342 Teoretický základ strojního inženýrství Studijní obor: Bez oboru Vedoucí práce: Ing. Pavol Vitkovič Ph.D. MOŽNOSTI VYTVÁŘENÍ VLN PRO SURFOVÁNÍ - II - PROHLÁŠENÍ Prohlašuji, že jsem tuto bakalářskou práci vypracoval samostatně s tím, že její výsledky mohou být dále použity podle uvážení vedoucího bakalářské práce jako jejího spoluautora. Souhlasím také s případnou publikací výsledků bakalářské práce nebo její podstatné části, pokud budu uveden jako její spoluautor. V Praze dne 17.8.2017 Prokop Daniel MOŽNOSTI VYTVÁŘENÍ VLN PRO SURFOVÁNÍ - III - PODĚKOVÁNÍ Zde bych rád srdečně poděkoval všem, kteří mě provázeli, motivovali a podporovali při mém studiu a při psaní této práce. Především děkuji vedoucímu mé bakalářské práce panu Ing. Pavolovi Vitkovičovi Ph.D. za cenné a užitečné rady, připomínky a čas strávený při konzultacích. V neposlední řadě děkuji také své rodině a přátelům za veškerou podporu projevenou během celého studia. MOŽNOSTI VYTVÁŘENÍ VLN PRO SURFOVÁNÍ - IV - ANOTAČNÍ LIST Jméno autora: Prokop DANIEL Název BP: Možnosti vytváření vln pro surfování Anglický název: Possibility of creating waves for surfing Rok: 2017 Studijní program: B2342 Teoretický základ strojního inženýrství Obor studia: bez oboru Ústav: Ústav mechaniky tekutin a termodynamiky Vedoucí BP: Ing. Pavol Vitkovič Ph.D. Bibliografické údaje: počet stran 39 počet obrázků 19 počet tabulek 02 počet příloh 00 Klíčová slova: surfing, wave pool, umělá vlna, vodní skok, riversurfing, statická vlna, mořské vzdouvání, příbojová vlna Keywords: surfing, wave pool, artificial wave, hydraulic jump, riversurfing, sheet flow wave, swell, ocean wave Anotace: Tématem této bakalářské práce je problematika tvorby umělých surfových vln. -
Makes Waves by Ansys Advantage Staff
FOCUS ON MULTIPHYSICS / SIMULATION-LED DESIGN Simulation-Driven Design Makes Waves By Ansys Advantage Staff Jakob Bergmeier surfing at the UNIT surf pool in September 2018 (www.surf-pool.com, photo credit: Paul Schöpplenberg) unich, Germany, may be best known as the world’s beer capital, but the landlocked city is also famous for another form of liquid refreshment: river surfing. The wet and often wild sport was invented in the Floßlände channel in Munich in the 1970s, and grew in popularity when a wave formed, somewhat by accident, on the Eisbach River Mas it flowed through the English Garden. To calm the rushing river’s current as it flowed through that tranquil park in central Munich, engineers placed concrete blocks into the water. The blocks had the unintended consequence of creating a fast, shallow, surfable wave. Surf fans began amplifying the wave’s force by tethering planks along the sides to narrow the channel. The result was Eisbachwelle, now Germany’s premier river surf destination. Unlike surfing on dynamic coastal waves, river surfing is done on standing waves, tidal bores or upstream waves. And while that might give the impression that river surfing is a tame facsimile of the ocean experience, the fact is that Eisbachwelle can be a bumpy ride, suitable for seasoned surfers only. Beginners can fine-tune their skills on the stationary wave at Floßlände, which is smoother and safer than the Eisbachwelle. Taking the entire concept of The geometry of the channel and stationary waves into a new dimension is Surf wave generation device is fully Langenfeld, where surfers of all levels can catch waves parameterized. -
Bend Whitewater Park Engineering, Commitment and a Quarter Million River Users
BEND WHITEWATER PARK ENGINEERING, COMMITMENT AND A QUARTER MILLION RIVER USERS UPGRADE: 2019 OSBEELS Symposium September 13, 2019 Salem, OR Don Horton Kevin Timmins, PE Executive Director Vice President OUTLINE • Introduction & Background • Constraints • Design & Permitting • How It Works • Results INTRODUCTION & BACKGROUND INTRODUCTORY VIDEO Bend Whitewater Park 2017 Design Award PROJECT OWNER & STAKEHOLDERS • Bend Park and Recreation District – Bend Paddle Trail Alliance – William Smith Properties – Upper Deschutes Watershed Council – City of Bend – Bend Surf Park Alliance PROJECT PURPOSE • River Trail and Paddle Trail • Deschutes River Trail Undercrossing • Replace Vehicle Bridge with Pedestrian Bridge • Fish Passage • Habitat Restoration • Whitewater Recreation SHEVLIN-HIXON MILL Deschutes Brewery McKay Park Dam Deschutes Historical Society archive MILL POND DAM C. 1918 Deschutes Historical Society archive HISTORY OF PROJECT • Safety Issues and Tragedies • BPTA Interest • Study of Locations, Scope • Partnership with William Smith Properties CONSTRAINTS UPSTREAM WATER LEVELS • Maintain “existing” upstream pool elevations • Monitored water levels for one year • Water supply intakes • Oregon Spotted Frog • 100-year Floodplain • Frazil Ice Management WHITEWATER CHANNEL • Three vs. Four waves • Something for everyone (kayak ability level) • Beginner at the bottom, advanced at the top • Something that is useable year-round • Add in River Surfing FISH PASSAGE CHANNEL • Oregon Fish Passage Laws • Provide safe passage for a variety of water craft and inner tubes • No upstream congestion • No access along channel vs. full access along channel HABITAT CHANNEL • Don’t disturb the right half of river • Add habitat complexity for birds • Shallow riffle vs. pool • 5cfs vs. 50 cfs vs. 100 cfs • Waterfalls • Vegetation but no trees DESIGN & PERMITTING HYDROLOGY HYDRAULIC MODELING • Reference Site Survey • 1D HEC-RAS • 2D for Whitewater Channel features • 3D for Surf Wave PERMITS • 404 Permit (US Army Corps of Engineers) • Removal/Fill Permit (Oregon Dept.