The Stone Space of a Boolean Ring
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Boolean Like Semirings
Int. J. Contemp. Math. Sciences, Vol. 6, 2011, no. 13, 619 - 635 Boolean Like Semirings K. Venkateswarlu Department of Mathematics, P.O. Box. 1176 Addis Ababa University, Addis Ababa, Ethiopia [email protected] B. V. N. Murthy Department of Mathematics Simhadri Educational Society group of institutions Sabbavaram Mandal, Visakhapatnam, AP, India [email protected] N. Amarnath Department of Mathematics Praveenya Institute of Marine Engineering and Maritime Studies Modavalasa, Vizianagaram, AP, India [email protected] Abstract In this paper we introduce the concept of Boolean like semiring and study some of its properties. Also we prove that the set of all nilpotent elements of a Boolean like semiring forms an ideal. Further we prove that Nil radical is equal to Jacobson radical in a Boolean like semi ring with right unity. Mathematics Subject Classification: 16Y30,16Y60 Keywords: Boolean like semi rings, Boolean near rings, prime ideal , Jacobson radical, Nil radical 1 Introduction Many ring theoretic generalizations of Boolean rings namely , regular rings of von- neumann[13], p- rings of N.H,Macoy and D.Montgomery [6 ] ,Assoicate rings of I.Sussman k [9], p -rings of Mc-coy and A.L.Foster [1 ] , p1, p2 – rings and Boolean semi rings of N.V.Subrahmanyam[7] have come into light. Among these, Boolean like rings of A.L.Foster [1] arise naturally from general ring dulity considerations and preserve many of the formal 620 K. Venkateswarlu et al properties of Boolean ring. A Boolean like ring is a commutative ring with unity and is of characteristic 2 with ab (1+a) (1+b) = 0. -
Ring (Mathematics) 1 Ring (Mathematics)
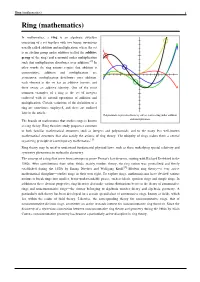
Ring (mathematics) 1 Ring (mathematics) In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition (called the additive group of the ring) and a monoid under multiplication such that multiplication distributes over addition.a[›] In other words the ring axioms require that addition is commutative, addition and multiplication are associative, multiplication distributes over addition, each element in the set has an additive inverse, and there exists an additive identity. One of the most common examples of a ring is the set of integers endowed with its natural operations of addition and multiplication. Certain variations of the definition of a ring are sometimes employed, and these are outlined later in the article. Polynomials, represented here by curves, form a ring under addition The branch of mathematics that studies rings is known and multiplication. as ring theory. Ring theorists study properties common to both familiar mathematical structures such as integers and polynomials, and to the many less well-known mathematical structures that also satisfy the axioms of ring theory. The ubiquity of rings makes them a central organizing principle of contemporary mathematics.[1] Ring theory may be used to understand fundamental physical laws, such as those underlying special relativity and symmetry phenomena in molecular chemistry. The concept of a ring first arose from attempts to prove Fermat's last theorem, starting with Richard Dedekind in the 1880s. After contributions from other fields, mainly number theory, the ring notion was generalized and firmly established during the 1920s by Emmy Noether and Wolfgang Krull.[2] Modern ring theory—a very active mathematical discipline—studies rings in their own right. -

Problems and Comments on Boolean Algebras Rosen, Fifth Edition: Chapter 10; Sixth Edition: Chapter 11 Boolean Functions
Problems and Comments on Boolean Algebras Rosen, Fifth Edition: Chapter 10; Sixth Edition: Chapter 11 Boolean Functions Section 10. 1, Problems: 1, 2, 3, 4, 10, 11, 29, 36, 37 (fifth edition); Section 11.1, Problems: 1, 2, 5, 6, 12, 13, 31, 40, 41 (sixth edition) The notation ""forOR is bad and misleading. Just think that in the context of boolean functions, the author uses instead of ∨.The integers modulo 2, that is ℤ2 0,1, have an addition where 1 1 0 while 1 ∨ 1 1. AsetA is partially ordered by a binary relation ≤, if this relation is reflexive, that is a ≤ a holds for every element a ∈ S,it is transitive, that is if a ≤ b and b ≤ c hold for elements a,b,c ∈ S, then one also has that a ≤ c, and ≤ is anti-symmetric, that is a ≤ b and b ≤ a can hold for elements a,b ∈ S only if a b. The subsets of any set S are partially ordered by set inclusion. that is the power set PS,⊆ is a partially ordered set. A partial ordering on S is a total ordering if for any two elements a,b of S one has that a ≤ b or b ≤ a. The natural numbers ℕ,≤ with their ordinary ordering are totally ordered. A bounded lattice L is a partially ordered set where every finite subset has a least upper bound and a greatest lower bound.The least upper bound of the empty subset is defined as 0, it is the smallest element of L. -

Mathematics 721 Fall 2016 on Dynkin Systems Definition. a Dynkin
Mathematics 721 Fall 2016 On Dynkin systems Definition. A Dynkin-system D on X is a collection of subsets of X which has the following properties. (i) X 2 D. (ii) If A 2 D then its complement Ac := X n A belong to D. 1 (iii) If An is a sequence of mutually disjoint sets in D then [n=1An 2 D. Observe that every σ-algebra is a Dynkin system. A1. In the literature one can also find a definition with alternative axioms (i), (ii)*, (iii)* where again (i) X 2 D, and (ii)* If A; B are in D and A ⊂ B then B n A 2 D. 1 (iii)* If An 2 D, An ⊂ An+1 for all n = 1; 2; 3;::: then also [n=1An 2 D. Prove that the definition with (i), (ii), (iii) is equivalent with the definition with (i), (ii)*, (iii)*. A2. Verify: If E is any collection of subsets of X then the intersection of all Dynkin-systems containing E is a Dynkin system containing E. It is the smallest Dynkin system containing E. We call it the Dynkin-system generated by E, and denote it by D(E). Definition: A collection A of subsets of X is \-stable if for A 2 A and B 2 A we also have A \ B 2 A. Observe that a \-stable system is stable under finite intersections. A3. (i) Show that if D is a \-stable Dynkin system, then the union of two sets in D is again in D. (ii) Prove: A Dynkin-system is a σ-algebra if and only if it is \-stable. -

Proto-Boolean Rings
An. S¸t. Univ. Ovidius Constant¸a Vol. 19(3), 2011, 175{194 Proto-Boolean rings Sergiu Rudeanu Abstract We introduce the family of R-based proto-Boolean rings associated with an arbitrary commutative ring R. They generalize the proto- Boolean algebra devised by Brown [4] as a tool for expressing in modern language Boole's research in The Laws of Thought. In fact the algebraic results from [4] are recaptured within the framework of proto-Boolean rings, along with other theorems. The free Boolean algebras with a fi- nite or countable set of free generators, and the ring of pseudo-Boolean functions, used in operations research for problems of 0{1 optimization, are also particular cases of proto-Boolean rings. The deductive system in Boole's Laws of Thought [3] involves both an alge- braic calculus and a \general method in Logic" making use of this calculus. Of course, Boole's treatises do not conform to contemporary standards of rigour; for instance, the modern concept of Boolean algebra was in fact introduced by Whitehead [12] in 1898; see e.g. [9]. Several authors have addressed the problem of presenting Boole's creation in modern terms. Thus Beth [1], Section 25 summarizes the approach of Hoff- Hansen and Skolem, who describe the algebra devised by Boole as the quotient of an algebra of polynomial functions by the ideal generated by x2 − x; y2 − y; z2 − z; : : : . Undoubtedly the most comprehensive analysis of the Laws of Thought is that offered by Hailperin [5] in terms of multisets. Quite recently, Brown [4], taking for granted the existence of formal entities described as polynomials with integer coefficients, subject to the usual computation rules 2 except that the indeterminates are idempotent (xi = xi), analyses Chapters V-X of [3] within this elementary framework, which he calls proto-Boolean algebra. -

On Ring-Like Structures of Lattice-Ordered Numerical Events
On ring-like structures of lattice-ordered numerical events Dietmar Dorninger and Helmut L¨anger Abstract Let S be a set of states of a physical system. The probabilities p(s) of the oc- currence of an event when the system is in different states s ∈ S define a function from S to [0, 1] called a numerical event or, more accurately, an S-probability. Sets of S-probabilities ordered by the partial order of functions give rise to so called al- gebras of S-probabilities, in particular to the ones that are lattice-ordered. Among these there are the σ-algebras known from probability theory and the Hilbert-space logics which are important in quantum-mechanics. Any algebra of S-probabilities can serve as a quantum-logic, and it is of special interest when this logic turns out to be a Boolean algebra because then the observed physical system will be classical. Boolean algebras are in one-to-one correspondence to Boolean rings, and the question arises to find an analogue correspondence for lattice-ordered algebras of S-probabilities generalizing the correspondence between Boolean algebras and Boolean rings. We answer this question by defining ring-like structures of events (RLSEs). First, the structure of RLSEs is revealed and Boolean rings among RLSEs are characterized. Then we establish how RLSEs correspond to lattice-ordered alge- bras of numerical events. Further, functions for associating lattice-ordered algebras of S-probabilities to RLSEs are studied. It is shown that there are only two ways to assign lattice-ordered algebras of S-probabilities to RLSEs if one restricts the corresponding mappings to term functions over the underlying orthomodular lat- tice. -

MULTIPLICATIVELY IDEMPOTENT SEMIRINGS 1. Introduction
140 (2015) MATHEMATICA BOHEMICA No. 1, 35–42 MULTIPLICATIVELY IDEMPOTENT SEMIRINGS Ivan Chajda, Olomouc, Helmut Länger, Wien, Filip Švrček, Olomouc (Received December 11, 2012) Abstract. Semirings are modifications of unitary rings where the additive reduct does not form a group in general, but only a monoid. We characterize multiplicatively idempotent semirings and Boolean rings as semirings satisfying particular identities. Further, we work with varieties of enriched semirings. We show that the variety of enriched multiplicatively idempotent semirings differs from the join of the variety of enriched unitary Boolean rings and the variety of enriched bounded distributive lattices. We get a characterization of this join. Keywords: semiring; commutative semiring; multiplicatively idempotent semiring; semir- ing of characteristic 2; simple semiring; unitary Boolean ring; bounded distributive lattice MSC 2010 : 16Y60, 06E20 1. Introduction Boolean rings are important algebras used both in mathematics and applications. Several characterizations of Boolean rings were settled in [1], [2] and [8]. However, in some considerations in Computer Science as well as in Propositional Calculus we need to work with similar algebras which need not be rings. In particular, we often use semirings satisfying the condition xx = x and hence forming a certain generalization of Boolean rings. Of course, every unitary Boolean ring is a semiring satisfying this condition. However, also every bounded distributive lattice can be considered as a semiring satisfying xx = x. Hence, our class of semirings under consideration is broad enough to be treated from several points of view. We recall the definition of a semiring from [5]. Support of the research of the first two authors by the Austrian Science Fund (FWF) and the Czech Science Foundation (GAČR), Project I 1923-N25, and by AKTION Austria– Czech Republic, Grant No. -

Some Fundamental Properties of Boolean Ring Normal Forms
Series Logo Volume 00 xx Some Fundamental Prop erties of Bo olean Ring Normal Forms Jieh Hsiang and Guan Shieng Huang Abstract Bo olean ring is an algebraic structure which uses exclusiv e or instead of the usual or It yields a unique normal form for every Bo olean function In this pap er we present several fundamental prop erties concerning Bo olean rings We present a simple metho d for deriving the Bo olean ring nor mal form directly from a truth table We also describ e a notion of normal form of a Bo olean function with a dontcare condition and show an algorithm for generating such a normal form We then discuss two Bo olean ring based theo rem proving metho ds for prop ositional logic Finally we give some arguments on why the Bo olean ring representation had not b een used more extensively and how it can b e used in computing Intro duction Bo olean ring is an algebraic structure which is equivalent to Bo olean algebra The ma jor representational dierences are that Bo olean ring uses exclusiveor instead of or to represent Bo olean functions and that there is no need for negation in Bo olean ring Furthermore there is a unique Bo olean ring normal form for every Bo olean function It is curious however that in spite of its long history and elegant algebraic prop erties the Bo olean ring representation has rarely b een used in the computational context In this pap er we present several fundamental results concerning Bo olean rings Some of the results are so elementary and simple that they can and should b e taught in a rstyear logic -

807 the Representation of Boolean Algebras
193*1 BOOLEAN ALGEBRAS 807 THE REPRESENTATION OF BOOLEAN ALGEBRAS M. H. STONE 1. Introduction. In this brief address I shall set myself a twofold aim: to review the theory of Boolean algebras, as we understand it today, and to sketch certain historical phases of its development. Al though I am in no sense prepared to offer the fruits of painstaking historical research, I believe that by a few pertinent historical ob servations I shall be able to bring out the underlying evolutionary pattern, which, in fact, is a quite familiar one. 2. Motivation and essential features of the theory. More than ninety years have passed since the publication of George Boole's first contribution towards an algebra of logic [5].* While Boole was by no means the first to attempt a symbolic method in logic (among his precursors we find Leibniz, Jacques and Jean Bernoulli, J. H. Lambert, and Gergonne [ó]) it is a just and proper tribute to his genius that we commonly call this algebra by his name. I believe it would be accurate to say that of the many books, memoirs, notes, and reviews (more than one hundred seventy-five in number [6]) which deal with Boolean algebras the great majority draw their in spiration directly or indirectly from the work of Boole. The orienta tion of these studies toward symbolic logic is apparent in their preoccupation with algorithms, identities, and equations, or with the logical interrelations of the formal properties of the various Boolean operations. Recently there has emerged a different tendency, namely, to view Boolean algebras structurally, as organic systems, rather than algorithmically. -

Representing Quantum Structures As Near Semirings 3
REPRESENTING QUANTUM STRUCTURES AS NEAR SEMIRINGS S. BONZIO, I. CHAJDA, AND A. LEDDA Abstract. In this paper we introduce the notion of near semir- ing with involution. Generalizing the theory of semirings we aim at represent quantum structures, such as basic algebras and ortho- modular lattices, in terms of near semirings with involution. In particular, after discussing several properties of near semirings, we introduce the so-calledLukasiewicz near semirings, as a particular case of near semirings, and we show that every basic algebra is representable as (precisely, it is term equivalent to) a near semir- ing. In the particular case in which aLukasiewicz near semiring is also a semiring, we obtain as a corollary a representation of MV- algebras as semirings. Analogously, by introducing a particular subclass ofLukasiewicz near semirings, that we termed orthomod- ular near semirings, we obtain a representation of orthomodular lattices. In the second part of the paper, we discuss several univer- sal algebraic properties ofLukasiewicz near semirings and we show that the variety of involutive integral near semirings is a Church variety. This yields a neat equational characterization of central elements of this variety. As a byproduct of such, we obtain several direct decomposition theorems for this class of algebras. 1. Introduction It is a long-dated result, due to Marshall Stone [19], that the theory of Boolean algebras (the algebraic counterpart of classical logic) can be framed within the theory of rigs, through the concept of Boolean ring. arXiv:1810.09345v1 [math.LO] 22 Oct 2018 More recently, in the last decade, the relations between prominent al- gebraic structures from many-valued logics and (semi)ring theory have stirred a renewed attention (see, e.g., [13, 1]). -

Neutrosophic Boolean Rings
Neutrosophic Sets and Systems Volume 33 Article 3 5-1-2020 Neutrosophic Boolean Rings T. Chalapathi L. Madhavi Follow this and additional works at: https://digitalrepository.unm.edu/nss_journal Recommended Citation Chalapathi, T. and L. Madhavi. "Neutrosophic Boolean Rings." Neutrosophic Sets and Systems 33, 1 (2020). https://digitalrepository.unm.edu/nss_journal/vol33/iss1/3 This Article is brought to you for free and open access by UNM Digital Repository. It has been accepted for inclusion in Neutrosophic Sets and Systems by an authorized editor of UNM Digital Repository. For more information, please contact [email protected], [email protected], [email protected]. Neutrosophic Sets and Systems, Vol. 33, 2020 University of New Mexico Neutrosophic Boolean Rings T.Chalapathi 1,* and L. Madhavi 2 1 Department of Mathematics, Sree Vidyanikethan Engg. College, Tirupati-517 102, Andhra Pradesh, India. [email protected] 2 Department of Applied Mathematics, Yogi Vemana University, Kadapa-516 003, Andhra Pradesh, India. [email protected] * Correspondence: [email protected]; Tel.: (+91 9542865332) Abstract: In this paper, we are going to define Neutrosophic Boolean rings and study their algebraic structure. A finite Boolean ring R satisfies the identity aa2 for all aR , which implies the identity aan for each positive integer n 1. With this as motivation, we consider a Neutrosophic Boolean ring NRI(,) which fulfils the identity ()a bI 2 a bI for all a bI N(,) R I and describes several Neutrosophic rings which are Neutrosophic Boolean rings with various algebraic personalities. First, we show a necessary and sufficient condition for a Neutrosophic ring of a classical ring to be a Neutrosophic Boolean ring. -

An Introduction to Boolean Algebras
California State University, San Bernardino CSUSB ScholarWorks Electronic Theses, Projects, and Dissertations Office of aduateGr Studies 12-2016 AN INTRODUCTION TO BOOLEAN ALGEBRAS Amy Schardijn California State University - San Bernardino Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd Part of the Algebra Commons Recommended Citation Schardijn, Amy, "AN INTRODUCTION TO BOOLEAN ALGEBRAS" (2016). Electronic Theses, Projects, and Dissertations. 421. https://scholarworks.lib.csusb.edu/etd/421 This Thesis is brought to you for free and open access by the Office of aduateGr Studies at CSUSB ScholarWorks. It has been accepted for inclusion in Electronic Theses, Projects, and Dissertations by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. An Introduction to Boolean Algebras A Thesis Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment of the Requirements for the Degree Master of Arts in Mathematics by Amy Michiel Schardijn December 2016 An Introduction to Boolean Algebras A Thesis Presented to the Faculty of California State University, San Bernardino by Amy Michiel Schardijn December 2016 Approved by: Dr. Giovanna Llosent, Committee Chair Date Dr. Jeremy Aikin, Committee Member Dr. Corey Dunn, Committee Member Dr. Charles Stanton, Chair, Dr. Corey Dunn Department of Mathematics Graduate Coordinator, Department of Mathematics iii Abstract This thesis discusses the topic of Boolean algebras. In order to build intuitive understanding of the topic, research began with the investigation of Boolean algebras in the area of Abstract Algebra. The content of this initial research used a particular nota- tion. The ideas of partially ordered sets, lattices, least upper bounds, and greatest lower bounds were used to define the structure of a Boolean algebra.