A Comparison of Rating Systems for Competitive Women's Beach Volleyball
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

July 31 QUOTES
2017 FIVB Beach Volleyball World Championships presented by A1 - July 31 QUOTES Women’s 55: Laura Ludwig / Kira Walkenhorst Germany (4) def. Karla Borger / Margareta Kozuch Germany (21) 21-19, 21-18 (0:40) Laura Ludwig, Germany – “We are definitely satisfied and happy that we won our first three matches. We are getting better and better in game rhythm. We need as many matches as you can get.” Kira Walkenhorst, Germany – “We need more games to get our performance back and find our rhythm. We are getting better game by game. Karla Borger, Germany – “They are still a normal team. We respect them a lot, but we can compete with them like everyone else…We love playing on center court. The fans enjoy what we do.” Margareta Kozuch, Germany – “We were pretty sure before the game that we could win. We knew it would be tough. We are disappointed that we lost, but we had a chance, even after a difficult start. We made too many mistakes, and we will learn from it.” Women's 61: Melissa Humana-Paredes / Sarah Pavan Canada (7) def. Fan Wang / Yuan Yue China (18) 21-16, 21-13 (0:34) Sarah Pavan, Canada – “For us, it wasn’t just enough to get through, we wanted to get through first in our pool just to set ourselves up for a good draw in the playoffs. China, they’ve got some serious abilities when they are working so we knew it was going to be a tough game. Luckily we put them in trouble with our serving there at the end and we were able to outlast them.” Melissa Humana-Paredes, Canada – “That was our goal coming into each game is that each game gets progressively better. -
Uniform Numbers
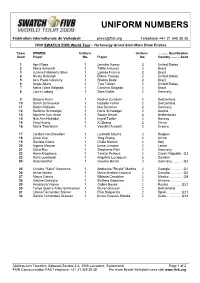
UNIFORM NUMBERS Fédération Internationale de Volleyball [email protected] Telephone +41-21 345 35 35 2009 SWATCH FIVB World Tour - 1to1energy Grand Slam Main Draw Entries Team WOMEN Uniform Uniform ........... Qualification Seed Player No. Player No. Country .......... Seed 1 April Ross 1 Jennifer Kessy 2 United States 2 Maria Antonelli 1 Talita Antunes 2 Brazil 3 Juliana Felisberta Silva 1 Larissa Franca 2 Brazil 4 Nicole Branagh 1 Elaine Youngs 2 United States 5 Ana Paula Connelly 1 Shelda Bede 2 Brazil 6 Angie Akers 1 Tyra Turner 2 United States 7 Maria Clara Salgado 1 Carolina Salgado 2 Brazil 8 Laura Ludwig 1 Sara Goller 2 Germany 9 Simone Kuhn 1 Nadine Zumkehr 2 Switzerland 10 Sarah Schmocker 1 Isabelle Forrer 2 Switzerland 11 Katrin Holtwick 1 Ilka Semmler 2 Germany 12 Stefanie Schwaiger 1 Doris Schwaiger 2 Austria 13 Marleen Van Iersel 1 Sanne Keizer 2 Netherlands 14 Nila Ann Hakedal 1 Ingrid Tørlen 2 Norway 15 Ying Huang 1 Xi Zhang 2 China 16 Maria Tsiartsiani 1 Vassiliki Arvaniti 2 Greece 17 Liesbet Van Breedam 1 Liesbeth Mouha 2 Belgium 18 Chen Xue 1 Ying Zhang 2 China 19 Daniela Gioria 1 Giulia Momoli 2 Italy 20 Inguna Minusa 1 Inese Jursone 2 Latvia 21 Okka Rau 1 Stephanie Pohl 2 Germany 22 Hana Klapalova 1 Tereza Petrova 2 Czech Republic . Q3 23 Karin Lundquist 1 Angelica Ljungquist 2 Sweden 24 Anja Gunther 1 Geeske Banck 2 Germany............ Q2 25 Cristine "Saka" Santanna 1 Andrezza "Rtvelo" Martins 2 Georgia.............. Q1 26 Annie Martin 1 Marie-Andree Lessard 2 Canada............. -

Foro Italico, 4-8 Settembre 2019
Foro Italico, 4-8 settembre 2019 Le Fivb Beach Finals al Foro Italico di Roma Il Foro Italico e la Capitale tornano protagonisti del circuito mondiale del beach volley. Dal 4 all’8 settembre, infatti, andranno in scena le Finals del World Tour 2019; ultimo appuntamento della stagione internazionale che vedrà scendere in campo le migliori coppie al mondo. Sulla sabbia capitolina ci saranno in palio fama, gloria, un ricco montepremi e molti, importanti punti validi per il ranking olimpico. Il Foro Italico, riconosciuto universalmente da atleti e addetti ai lavori come una delle migliori location del pianeta, torna dunque alle luci della ribalta a distanza di cinque anni dall’ultimo Grand Slam organizzato nel 2013. Il primo ciclo di joint ventur tra Federazione Italiana Pallavolo e l’allora CONI Servizi SpA diede vita a un quinquennio di grandi eventi tra i quali i Campionati del Mondo del 2011 che sancirono la consacrazione in Italia della disciplina più seguita ai Giochi Olimpici. La rassegna iridata fece registrare numeri importanti in termini di partecipazione di pubblico; un boom che contribuì successivamente all’ingresso della pallavolo nel complesso sportivo italiano (2014 Italia-Polonia e 2015 Italia-Brasile di World League; 2018 l’esordio degli azzurri nei Campionati del Mondo sotto lo sguardo del Presidente della Repubblica) che ha così accolto nella sua lunga storia un numero sempre maggiore di discipline. L’attesa è notevole dunque per un evento che spera di celebrare un grande risultato in termini di pubblico, di seguito e sperando in una affermazione delle coppie italiane che mai sono salite sul gradino più alto del podio a Roma. -

2019 FIVB WORLD CHAMPIONSHIPS Presented by Comdirect & ALDI Nord
2019 FIVB WORLD CHAMPIONSHIPS presented by comdirect & ALDI Nord Sunday, June 30 - Men’s & Women’s Pool Play Schedule Match No. Time Court Team A Team B Gender Round 27 13:00 1 Fijalek/Bryl POL [2] Bergmann/Harms, Y. GER [26] Men Pool B 30 14:00 1 Behrens/Tillmann GER [22] Bausero/Rotti URU [46] Women Pool C 33 15:00 1 Klineman/Ross USA [5] Xue/Wang X. X. CHN [29] Women Pool E 34 16:00 1 Borger/Sude GER [20] Mendoza/Lolette NCA [44] Women Pool E 25 17:00 1 Mol, A./Sørum, C. NOR [1] Erdmann/Winter GER [25] Men Pool A 31 18:00 1 Ana Patrícia/Rebecca BRA [4] Bieneck/Schneider GER [28] Women Pool D 35 19:15 1 Dalhausser/Lucena USA [6] Saxton/O'Gorman CAN [30] Men Pool F 43 20:30 1 Maria Antonelli/Carol BRA [10] Kozuch/Ludwig GER [34] Women Pool J 35 10:00 2 Agatha/Duda BRA [6] Ishii/Murakami JPN [30] Women Pool F 37 11:00 2 Clancy/Artacho Del Solar AUS [7] Stubbe, J./van Iersel NED [31] Women Pool G 39 12:00 2 Keizer/Meppelink NED [8] Laird/Palmer AUS [32] Women Pool H 41 13:00 2 Pavan/Melissa CAN [9] Ukolova/Birlova RUS [33] Women Pool I 29 14:00 2 Bansley/Brandie CAN [3] Heidrich/Vergé-Dépré, A. SUI [27] Women Pool C 39 15:00 2 Nicolai/Lupo ITA [8] Seidl Rob./Waller AUT [32] Men Pool H 33 16:00 2 Semenov/Leshukov RUS [5] Allen/Slick USA [29] Men Pool E 26 17:00 2 Pedro Solberg/Vitor Felipe BRA [24] Gonzalez/Reyes CUB [48] Men Pool A 37 18:00 2 Gibb/Crabb Ta. -
POOL WATER: Cause Behind Sudden Color Change Still Unknown
Page 2B East Oregonian SPORTS Wednesday, August 10, 2016 Olympics Phelps swims to two more golds, Ledecky adds one By GENARO C. ARMAS Williams shanked shots all Host country Brazil Associated Press over the court in getting played to a 0-0 draw with upset by Elina Svitolina of South Africa. The Brazilians RIO DE JANEIRO — Ukraine. The top-ranked had already secured a spot Good old Michael Phelps, American won’t get a chance in the women’s soccer quar- golden again. to defend the gold she won in terinals before their match. For teenagers Katie London. Williams looked out The team and star Marta Ledecky and Simone Biles, of sorts and irritated, accu- have drawn more attention their star turns in the Summer mulating 37 unforced errors. while Brazil’s men have Olympics might be just She had ive double-faults in struggled at the Olympics. beginning. one game alone in the 6-4, The women’s team will face From the pool to the 6-3 loss to the 20th-ranked Australia in a quarterinal gymnastics loor, Team USA Svitolina. Williams wiped match on Friday. had nice day at the Rio de her forehead, picked up RUGBY STUNNER : Janeiro Games. her rackets and headed Sonny Bill Williams was Not all the American back quickly to the locker helped off with an ankle stars were winners Tuesday, room. Svitolina, who had injury during New Zealand’s though. Serena Williams lost never before played in an shocking 14-12 loss to on the tennis court and the Olympics, smiled and stuck Japan in its irst game of U.S. -

Diese Frauenteams Kämpfen Um Die Meisterschaft: Die Deutschen Top 16 - Meldelistenplatz 1 - 4
Diese Frauenteams kämpfen um die Meisterschaft: Die Deutschen Top 16 - Meldelistenplatz 1 - 4 1. Sara Goller / Laura Ludwig (Hertha BSC) Sie sind und bleiben unangefochten Deutschlands Nummer 1. Bei den Olympischen Spielen - bei denen sie Fünfte wurden - und beim smart beach tour SuperCup auf Norderney setzten sich die amtierenden Deutschen Meisterinnen gegen Katrin Holtwick und Ilka Semmler durch. Ihr bestes internationales Ergebnis holten sie mit Silber Mitte Juni beim Grand Slam in Rom. Beim „Heim Grand Slam“ in Berlin wurden Goller/Ludwig Neunte. Insgesamt holte das Hauptstadt-Duo so viele Meistertitel, wie noch kein anderes Frauenteam zuvor: vier! 2. Katrin Holtwick / Ilka Semmler (Seaside Beach Club Essen) Früh in der Saison haben Katrin Holtwick und Ilka Semmler die Qualifikation für die Olympischen Spiele perfekt gemacht. Seit 2006 bilden die beiden ein Team und holten 2009 ihren ersten und bislang einzigen Meistertitel. Bei den letzten nationalen Meisterschaften wurden sie Vierte. Auf internationaler Ebene errangen sie als bestes deutsches Team Rang Vier beim smart Grand Slam in Berlin und in Peking. Für Katrin Holtwick ist es die 10. Teilnahme, Ilka Semmler wird zum 8. Mal teilnehmen (ihr Debut gab sie 2004 an der Seite von Sara Goller). 3. Karla Borger / Britta Büthe (MTV Stuttgart) Nicht nur, dass Karla Borger und Britta Büthe bei den letzten Deutschen smart Beach-Volleyball Meisterschaften Rang 3 erspielten, sie haben diese Position auch im zweiten Jahr in Folge in der deutschen Rangliste inne. Zwar machten sie sich bei ihren deutschen Fans rar, doch international zeigten sie wie 2011 ihre Klasse. Das Ziel ist für Britta Büthe klar: „Nachdem es uns letztes Jahr auf dem Treppchen gut gefallen hat, wollen wir natürlich wieder aufs Podium! Wir freuen uns riesig auf viele bekannten Gesichter, Familie und Freunde!“ 4. -

FIVB Beach Volleyball Swatch World Tour Smart Grand Slam - Rome 2012
FIVB Beach Volleyball Swatch World Tour smart Grand Slam - Rome 2012 A Roma i grandi campioni del beach volley mondiale Torna a Roma il grande beach volley internazionale. Dopo l’incredibile successo dei Campionati del Mondo dello scorso anno, quando 10 mila spettatori hanno gremito gli spalti del campo centrale per assistere alle finali, la Capitale è pronta ad accogliere i più forti giocatori del grande circo sulla sabbia impegnati nello FIVB Beach Volleyball Swatch World Tour smart Grand Slam - Rome 2012. Quella che si terrà nel Parco del Foro Italico, dal 12 al 17 giugno, sarà una delle tappe principali della stagione, l’ottavo appuntamento del World Tour 2012 dopo Brasilia, Sanya, Myslowice, Shanghai, Pechino, Praga, Mosca e il quarto degli otto Grand Slam in programma quest’anno cui seguiranno quelli di Gstaad, Berlino, Klagenfurt e Stare Jablonki. Un torneo maschile e femminile con un montepremi complessivo di 600mila dollari, una vera e propria parata di stelle con 171 formazioni iscritte provenienti da 34 diversi Paesi, comprese tutte quelle che occupano i primi posti del ranking olimpico. Tra i beachers che solcheranno la sabbia del Foro Italico ci saranno le due coppie brasiliane che hanno trionfato proprio a Roma nella rassegna iridata dello scorso anno: Alison-Emanuel nel tabellone maschile e Larissa –Juliana in quello femminile. Insieme a loro tanti altri fuoriclasse come gli olimpionici Rogers-Dalhausser (vincitori nello Slam capitolino di due anni fa) e le connazionali May Treanor-Walsh, anche loro medaglia d’oro ai Giochi di Pechino del 2008. Tra le donne molta attesa per le forti cinesi Xue-Zhang, le tedesche Goller-Ludwig, le olandesi campionesse continentali in carica Keizer-Van Iersel e ancora le atlete a stelle e strisce Kessy-Ross che trionfarono proprio nella Capitale nello Slam del 2010. -

Volleyballtraining Spitzenbereich ... Ist Der Lieblingsbegriff, Mit Dem
Volleyballtraining Spitzenbereich Anett Szigeti ist für die sportpsychologische Betreuung Erstes Gruppenspiel gegen verantwortlich und begleitet das Team bei vielen Turnieren. Elghobashy/Nada (EGY), 2:0 (21:12, 21:15) Neben diesen fixen Größen wurde das Team in Rio durch den Thema: Erster Einsatz bei Olympischen Spielen Scout Ron Gödde und Physiotherapeut Jochen Dirksmeier Für Kira Walkenhorst bedeutete das Spiel gegen Ägypten komplettiert. Weitere Mitarbeiter des DVV und aus dem den ersten Auftritt bei Olympischen Spielen, während Laura medizinischen Bereich waren in Rio für alle deutschen Ludwig bereits in Peking und London dabei war. Deutsche Beachvolleyballer zuständig. Die Bedeutung des Teams um Beachvolleyballer schafften es bislang nie, bei ihrer ersten das Team stellte Laura Ludwig nach dem Finalsieg heraus: Olympiateilnahme die beste Leistung zu zeigen. Medaillen- „Jürgen hat uns beigebracht, handlungsorientiert zu denken gewinner Brink, Reckermann, Ahmann und Hager brachten (siehe Seite 15). Helke und Anett haben geholfen, uns auf ihre Topleistung alle erst beim zweiten Turnier. alle Situationen vorzubereiten. Die medizinische Abteilung Ein großer Vorteil für Kira Walkenhorst war, dass Wagner hat großartige Arbeit geleistet: Nach dem Halbfinale habe und Laura Ludwig schon Olympiaerfahrung hatten und sie Triumphmarsch im Sand ich mich sehr müde gefühlt, heute wie 25.“ gut auf den Mythos vorbereiten konnten. Zudem begleitete der Copacabana: Die Formsteuerung ist ein Steckenpferd von Wagner. Dem Teampsychologin Anett Szigeti das Duo bereits während der Ludwig/Walkenhorst Trainer gelang es erneut, seine Spielerinnen athletisch auf Qualifikationsphase intensiv und stimmte es auf Rio ein. Sie machten alles richtig. Mit den Punkt fit zu bekommen. Selbst innerhalb des Turniers brachte ihre Athletinnen mental dazu, ihr Leistungspotenzial einem Wort: Sensationell! war ein Anstieg zu erkennen, besonders Kira Walkenhorst unter besonderen Bedingungen auszuschöpfen. -

Beach Volleyball World Championships - Hamburg, Germany
TEAM CANADA PREVIEW 2019 FIVB Beach Volleyball World Championships - Hamburg, Germany It’s hard to believe that with all of Canada’s international success on the beach, there has never been a medal at the World Championships – at the senior level. Could this be the year? Canada will be represented by five high quality teams in a field of 96 teams (48 men/48 women) at the 2019 FIVB Beach Volleyball World Championships which run from Friday, June 28 until Sunday, July 7 at the Red Bull Beach Arena in Hamburg, Germany. It’s the same venue that has successfully hosted the last two World Tour Finals. On the women’s side, there are two Canadian pairs with proven pedigree at the world level and either team – or both – could be in the mix for the medals. Canada has another women’s team that has been turning heads through the junior and collegiate ranks as well. At the 2017 World Championships in Vienna, the Canadian duo of Sarah Pavan (Kitchener, ON) and Melissa Humana-Paredes (Toronto, ON) made it to the bronze medal match, but landed 4th after a heart-breaking loss to Larissa Franca and Talita Antunes when the Brazilians took the 3rd set by an 18-16 score. The Pavan/Melissa pairing has spent time at #1 in the World Tour rankings thanks to wins in Croatia, China and Switzerland and has made eight trips to a World Tour podium in just 25 tournaments together. Probably most impressive was the win at the Five-Star Gstaad Major where they went undefeated in six matches including victories over American, Brazilian and German teams - on the march to gold. -

Final Four Notes
Fédération Internationale de Volleyball [email protected] Telephone +41.21.345.3535 Semi Finals - Larissa Franca/Talita Antunes, Brazil vs. Natalia Dubovcova/Dominika Nestarcova, Slovak Republic Larissa França Maestrini Talita Da Rocha Antunes Personal Info Personal Info Birth Date: April 14, 1982 (34 yrs old) Birth Date: August 29, 1982 (33 yrs old) Home Town: Fortaleza Home Town: Rio de Janeiro Resides: Fortaleza Resides: Rio de Janeiro Height: 174 cm (5'9") Height: 181 cm (5'11") Weight: 68 kg (151 lbs.) Weight: 65 kg (144 lbs.) Seasons: 14 Seasons: 14 Photo:FIVB Photo:FIVB Tournaments: 137 Tournaments: 153 Best Finish: 1st (58 times) Best Finish: 1st (30 times) Career Winnings: $1,731,235 Career Winnings: $1,349,725 Team Career Summary Tour Played 1 2 3 4 5 7 9 13 17 25 Money FIVB 22 12 1 1 0 1 0 6 0 0 0 US$768,000.00 Previous Olsztyn Results Year Partner - Result Partner - Result 2015 Talita Antunes - 1st Larissa Franca - 1st Olsztyn Matches Date Bracket Opponent Score Time Wed, 6/15/2016 Pool B Katarzyna Kociolek / Martyna Wardak, Poland (31) Won 21-9, 21-6 0:22 Thu, 6/16/2016 Pool B Fan Wang / Yuan Yue, China (18) Won 21-18, 21-16 0:31 Thu, 6/16/2016 Pool B Sophie van Gestel / Jantine van der Vlist, Netherlands (15) Won By Forfeit Fri, 6/17/2016 Winner 2 Katrin Holtwick / Ilka Semmler, Germany (11) Won 21-12, 21-15 0:28 Fri, 6/17/2016 Winner 3 Lauren Fendrick / Brooke Sweat, United States (8) Won 21-13, 21-10 0:24 Sat, 6/18/2016 Semi-Finals Natalia Dubovcova / Dominika Nestarcova, Slovak Republic (23) Larissa Franca and Talita Antunes have been playing together since 2014. -

❸Opposites. ❷Olympics Roster Spots. Who Will
COLLEGE PREP: A WORKOUT TO EASE THE TRANSITION FROM HIGH SCHOOL TO COLLEGE APRIL 2016 ❸ OPPOSITES. ❷ OLYMPICS ROSTER SPOTS. WHO WILL KARCH CHOOSE? KHALIAKHALIA LANIERLANIERHeadlines the Girls’ Fab 50 GET TO KNOW ITALY’S MARTA MENEGATTI PHOTO CREDIT PHOTO INDUSTRY’S #1 MAGAZINE March/April 2016 | VOLLEYBALLMAG.COM | A #USAVolley2016 If you’re serious about volleyball, you need VERT. The most advanced wearable jump technology for players and coaches. Motivate, manage jump load, and most importantly… prevent injuries. Karch Kiraly Head Coach, USA Women’s National Team “VERT allows us to track our training loads in a way that’s never been done before. It’s already helping us train SMARTER and better preserve our most precious resource: our ATHLETES and their HEALTH.” The official Jump Technology of @VERT I USAVERT.com I 510.629.3665 65 Mayfonk Athletic LLC covered by U.S. Patent nos. 8,253,586, 8,860,584 and other patent(s) pending. Designed for iPhone® 6Plus, iPhone 6, iPhone 5s, iPhone 5c, iPhone 5, iPhone 4s, iPod touch® (5th Gen), iPad Air, iPad mini, iPad® (3rd and 4th Gen). Apple and the Apple logo are trade marks of Apple Inc registered in the US and other countries. MARCH/APRIL 2016 Volume 27, Issue 2 VOLLEYBALL MAGAZINE FEATURES 40 20 BUILD YOUR BASE Five basic moves all high school athletes should master before graduation. By Tony Duckwall 24 X FACTOR High school senior Khalia Lanier brings it to every competition—for Team USA, Arizona Storm, and Xavier Prep High School—and soon she’ll take her talents to USC. -

Using Bayesian Statistics to Rank Sports Teams (Or, My Replacement for the BCS)
Ranking Systems The Bradley-Terry Model The Bayesian Approach Using Bayesian statistics to rank sports teams (or, my replacement for the BCS) John T. Whelan [email protected] Center for Computational Relativity & Gravitation & School of Mathematical Sciences Rochester Institute of Technology π-RIT Presentation 2010 October 8 1/38 John T. Whelan [email protected] Using Bayesian statistics to rank sports teams Ranking Systems The Bradley-Terry Model The Bayesian Approach Outline 1 Ranking Systems 2 The Bradley-Terry Model 3 The Bayesian Approach 2/38 John T. Whelan [email protected] Using Bayesian statistics to rank sports teams Ranking Systems The Bradley-Terry Model The Bayesian Approach Outline 1 Ranking Systems 2 The Bradley-Terry Model 3 The Bayesian Approach 2/38 John T. Whelan [email protected] Using Bayesian statistics to rank sports teams Ranking Systems The Bradley-Terry Model The Bayesian Approach The Problem: Who Are The Champions? The games have been played; crown the champion (or seed the playoffs) If the schedule was balanced, it’s easy: pick the team with the best record If schedule strengths differ, record doesn’t tell all e.g., college sports (seeding NCAA tourneys) 3/38 John T. Whelan [email protected] Using Bayesian statistics to rank sports teams Ranking Systems The Bradley-Terry Model The Bayesian Approach Evaluating an Unbalanced Schedule Most NCAA sports (basketball, hockey, lacrosse, . ) have a selection committee That committee uses or follows selection criteria (Ratings Percentage Index, strength of schedule, common opponents, quality wins, . ) Football (Bowl Subdivision) has no NCAA tournament; Bowl Championship Series “seeded” by BCS rankings All involve some subjective judgement (committee or polls) 4/38 John T.