DOCSLIB.ORG

Binary Representation Number Systems Positional Notation Base

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Binary Representation Number Systems Positional Notation Base Binary Representation Number Systems • The basis of all digital data is binary representation. • To talk about binary data, we must first talk about • Binary - means ‘two’ number systems –1, 0 –True, False • The decimal number system (base 10) you should be familiar with! –Hot, Cold – A digit in base 10 ranges from 0 to 9. –On, Off – A digit in base 2 ranges from 0 to 1 (binary number • We must be able to handle more than just values for system). A digit in base 2 is also called a ‘bit’. real world problems – A digit in base R can range from 0 to R-1 – 1, 0, 56 – A digit in Base 16 can range from 0 to 16-1 – True, False, Maybe (0,1,2,3,4,5,5,6,7,8,9,A,B,C,D,E,F). Use letters A-F to – Hot, Cold, LukeWarm, Cool represent values 10 to 15. Base 16 is also called – On, Off, Leaky Hexadecimal or just ‘Hex’. V 0.1 1 V 0.1 2 Positional Notation Base 10, Base 2, Base 16 Value of number is determined by multiplying each digit by a The textbook uses subscripts to represent different weight and then summing. The weight of each digit is a bases (ie. A2F16 , 953.7810, 1011.112 ) POWER of the BASE and is determined by position. I will use special symbols to represent the different bases. The default base will be decimal, no special symbol for 953.78 = 9 x 102 + 5 x 101 + 3 x 100 + 7 x 10-1 + 8 x 10-2 base 10. = 900 + 50 + 3 + .7 + .08 = 953.78 The ‘$’ will be used for base 16 ( $A2F) Will also use ‘h’ at end of number (A2Fh) % 1011.11 = 1x23 + 0x22 + 1x21 + 1x20 + 1x2-1 + 1x2-2 The ‘%’ will be used for base 2 (%10101111) = 8 + 0 + 2 + 1 + 0.5 + 0.25 = 11.75 If ALL numbers on a page are the same base (ie, all in base $ A2F = 10x162 + 2x161 + 15x160 16 or base 2 or whatever) then no symbols will be used and = 10 x 256 + 2 x 16 + 15 x 1 a statement will be present that will state the base (ie, all = 2560 + 32 + 15 = 2607 numbers on this page are in base 16). V 0.1 3 V 0.1 4 Common Powers Conversion of Any Base to Decimal 2-3 = 0.125 Converting from ANY base to decimal is done by multiplying 0 0 2-2 = 0.25 16 = 1 = 2 each digit by its weight and summing. 2-1 = 0.5 161 = 16 = 24 20 = 1 162 = 256 = 28 1 2 = 2 163 = 4096 = 212 Binary to Decimal 22 = 4 23 = 8 % 1011.11 = 1x23 + 0x22 + 1x21 + 1x20 + 1x2-1 + 1x2-2 24 = 16 = 8 + 0 + 2 + 1 + 0.5 + 0.25 25 =32 26 = 64 = 11.75 27 = 128 210 = 1024 = 1 K 8 2 = 256 220 = 1048576 = 1 M (1 Megabits) = 1024 K = 210 x 210 Hex to Decimal 29 = 512 230 = 1073741824 = 1 G (1 Gigabits) 210 = 1024 A2Fh = 10x162 + 2x161 + 15x160 211 = 2048 = 10 x 256 + 2 x 16 + 15 x 1 212 = 4096 = 2560 + 32 + 15 = 2607 V 0.1 5 V 0.1 6 1 Conversion of Decimal Integer To ANY Base Least Significant Digit Divide Number N by base R until quotient is 0. Remainder at Most Significant Digit EACH step is a digit in base R, from Least Significant digit to Most significant digit. Convert 53 to binary 53 = % 110101 53/2 = 26, rem = 1 Least Significant Digit 26/2 = 13, rem = 0 13/2 = 6 , rem = 1 6 /2 = 3, rem = 0 Most Significant Digit Least Significant Digit 5 3/2 = 1, rem = 1 (has weight of 2 or (has weight of 20 or 1). 1/2 = 0, rem = 1 Most Significant Digit 32). For base 2, also For base 2, also called called Most Significant Least Significant Bit 53 = % 110101 Bit (MSB). Always (LSB). Always = 1x25 + 1x24 + 0x23 + 1x22 + 0x21 + 1x20 LEFTMOST digit. RIGHTMOST digit. = 32 + 16 + 0 + 4 + 0 + 1 = 53 V 0.1 7 V 0.1 8 More Conversions Hex (base 16) to Binary Conversion Convert 53 to Hex Each Hex digit represents 4 bits. To convert a Hex number to Binary, simply convert each Hex digit to its four bit value. 53/16 = 3, rem = 5 Hex Digits to binary: 3 /16 = 0 , rem = 3 Hex Digits to binary (cont): $ 0 = % 0000 $ 9 = % 1001 53 = 35h $ 1 = % 0001 $ A = % 1010 1 0 $2 = % 0010 = 3 x 16 + 5 x 16 $ B = % 1011 = 48 + 5 = 53 $3 = % 0011 $ C = % 1100 $4 = % 0100 $ D = % 1101 $5 = % 0101 $ E = % 1110 $6 = % 0110 $ F = % 1111 $7 = % 0111 $8 = % 1000 V 0.1 9 V 0.1 10 A Trick! Hex to Binary, Binary to Hex If faced with a large binary number that has to be converted to decimal, I first convert the binary number A2Fh = % 1010 0010 1111 to HEX, then convert the HEX to decimal. Less work! 345h = % 0011 0100 0101 % 110111110011 = % 1101 1111 0011 = D F 3 Binary to Hex is just the opposite, create groups of 4 bits = 13 x 162 + 15 x 161 + 3x160 starting with least significant bits. If last group does not = 13 x 256 + 15 x 16 + 3 x 1 have 4 bits, then pad with zeros for unsigned numbers. = 3328 + 240 + 3 = 3571 % 1010001 = % 0101 0001 = 51h Of course, you can also use the binary, hex conversion feature on your calculator. Too bad calculators won’t be allowed on Padded with a zero the first test, though…... V 0.1 11 V 0.1 12 2 Binary Numbers Again Binary Arithmetic, Subtraction The rules for binary arithmetic The rules for binary subtraction Recall than N binary digits (N bits) can represent unsigned are: are: integers from 0 to 2N-1. 0 + 0 = 0, carry = 0 0 - 0 = 0, borrow = 0 4 bits = 0 to 15 1 + 0 = 1, carry = 0 1 - 0 = 1, borrow = 0 8 bits = 0 to 255 16 bits = 0 to 65535 0 + 1 = 1, carry = 0 0 - 1 = 1, borrow = 1 Besides simply representation, we would like to also do 1 + 1 = 0, carry = 1 1 - 1 = 0, borrow = 0 arithmetic operations on numbers in binary form. Principle operations are addition and subtraction. Borrows, Carries from digits to left of current of digit. Binary subtraction, addition works just the same as decimal addition, subtraction. V 0.1 13 V 0.1 14 Subtraction Binary, Decimal addition Decimal Binary Binary Decimal 900 % 100 % 101011 34 - 001 - % 001 + % 000001 ------- ------- + 17 --------------- 899 011 ------ 101100 51 From LSB to MSB: 0-1 = 9; with borrow of 1 0-1 = 1; with borrow of 1 from LSD to MSD: 1+1 = 0, carry of 1 from next column from next column 7+4 = 1; with carry out of 1 1 (carry)+1+0 = 0, carry of 1 0 -1 (borrow) - 0 = 9, with 0 -1 (borrow) - 0 = 1, with to next column 1 (carry)+0 + 0 = 1, no carry borrow of 1 borrow of 1 1 +0 = 1 9 - 1 (borrow) - 0 = 8. 0 + 0 = 0 1 - 1 (borrow) - 0 = 0. 1 (carry) + 3 + 1 = 5. Answer = 899. Answer = % 011. 1 + 0 = 1 answer = 51. answer = % 101100 V 0.1 15 V 0.1 16 Hex Addition Hex addition again Why is Ah + 8h = 2 with a carry out of 1? Decimal check. 3Ah The carry out has a weight equal to the BASE (in this case 3Ah = 3 x 16 + 10 16). The digit that gets left is the excess (BASE - sum). + 28h = 58 -------- 28h = 2 x 16 + 8 Ah + 8h = 10 + 8 = 18. 62h = 40 58 + 40 = 98 18 is GREATER than 16 (BASE), so need a carry out! A+8 = 2; with carry out of 1 to next column Excess is 18 - BASE = 18 - 16 = 2, so ‘2’ is digit. 62h = 6 x 16 + 2 Exactly the same thing happens in Decimal. = 96 + 2 = 98!! 1 (carry) + 3 + 2 = 6. 5 + 7 = 2, carry of 1. answer = $ 62. 5 + 7 = 12, this is greater than 10!. So excess is 12 - 10 = 2, carry of 1. V 0.1 17 V 0.1 18 3 Hex Subtraction Hex subtraction again Decimal check. 34h Why is 4h – 7h = $D with a borrow of 1? 34h = 3 x 16 + 4 - 27h = 52 The borrow has a weight equal to the BASE (in this case -------- 27h = 2 x 16 + 7 16). 0Dh = 39 52 - 39 = 13 BORROW +4h – 7h = 16 + 4 -7 = 20 -7 = 13 = Dh. 4-7 = D; with borrow of 1 from next column Dh is the result of the subtraction with the borrow. 0Dh = 13 !! Exactly the same thing happens in decimal. 3 - 1 (borrow) - 2 = 0. 3 - 8 = 5 with borrow of 1 answer = $ 0D. borrow + 3 - 8 = 10 + 3 - 8 = 13 - 8 = 5. V 0.1 19 V 0.1 20 Fixed Precision Unsigned Overflow With paper and pencil, I can write a number with as many digits as I want: In this class I will use 8 bit precision most of the time, 16 bit 1,027,80,032,034,532,002,391,030,300,209,399,302,992,092,920 occassionally. A microprocessor or computing system usually uses FIXED Overflow occurs when I add or subtract two numbers, and the PRECISION for integers; they limit the numbers to a fixed correct result is a number that is outside of the range of number of bits: allowable numbers for that precision. I can have both $ AF4500239DEFA231 64 bit number, 16 hex digits unsigned and signed overflow (more on signed numbers later) $ 9DEFA231 32 bit number, 8 hex digits $ A231 16 bit number, 4 hex digits 8 bits -- unsigned integers 0 to 28 -1 or 0 to 255.
Load more

Recommended publications
  • Nondecimal Positional Systems
    M03_LONG0847_05_AIE_C03.qxd 9/17/07 10:38 AM Page 162 Not for Sale 162 CHAPTER 3 Numeration and Computation 3.2 Nondecimal Positional Systems In the preceding section, we discussed several numeration systems, including the decimal system in common use today. As already mentioned, the decimal system is a positional system based on 10. This is probably so because we have ten fingers and historically, as now, people often counted on their fingers. In the Did You Know box at the end of this section, we will give applications of positional systems that are based on whole numbers other than 10. One very useful application of bases other than ten is as a way to deepen our understanding of number systems, arithmetic in general, and our own decimal system. Although bases other than ten were in the K–5 curriculum in the past, they are not present currently. However, nondecimal positional systems are studied in the “math methods” course that is a part of an elementary education degree and may return to elementary school in the future. We will discuss addition and subtraction in base five in the next section and multiplication in base six in the following one. Base Five Notation For our purposes, perhaps the quickest route to understanding base five notation is to reconsider the abacus of Figure 3.1. This time, however, we allow only 5 beads to be moved forward on each wire. As before, we start with the wire to the students’ right (our left) and move 1 bead forward each time as we count 1, 2, 3, and so on.
    [Show full text]
  • 13054-Duodecimal.Pdf
    Universal Multiple-Octet Coded Character Set International Organization for Standardization Organisation Internationale de Normalisation Международная организация по стандартизации Doc Type: Working Group Document Title: Proposal to encode Duodecimal Digit Forms in the UCS Author: Karl Pentzlin Status: Individual Contribution Action: For consideration by JTC1/SC2/WG2 and UTC Date: 2013-03-30 1. Introduction The duodecimal system (also called dozenal) is a positional numbering system using 12 as its base, similar to the well-known decimal (base 10) and hexadecimal (base 16) systems. Thus, it needs 12 digits, instead of ten digits like the decimal system. It is used by teachers to explain the decimal system by comparing it to an alternative, by hobbyists (see e.g. fig. 1), and by propagators who claim it being superior to the decimal system (mostly because thirds can be expressed by a finite number of digits in a "duodecimal point" presentation). • Besides mathematical and hobbyist publications, the duodecimal system has appeared as subject in the press (see e.g. [Bellos 2012] in the English newspaper "The Guardian" from 2012-12-12, where the lack of types to represent these digits correctly is explicitly stated). Such examples emphasize the need of the encoding of the digit forms proposed here. While it is common practice to represent the extra six digits needed for the hexadecimal system by the uppercase Latin capital letters A,B.C,D,E,F, there is no such established convention regarding the duodecimal system. Some proponents use the Latin letters T and E as the first letters of the English names of "ten" and "eleven" (which obviously is directly perceivable only for English speakers).
    [Show full text]
  • Positional Notation Or Trigonometry [2, 13]
    The Greatest Mathematical Discovery? David H. Bailey∗ Jonathan M. Borweiny April 24, 2011 1 Introduction Question: What mathematical discovery more than 1500 years ago: • Is one of the greatest, if not the greatest, single discovery in the field of mathematics? • Involved three subtle ideas that eluded the greatest minds of antiquity, even geniuses such as Archimedes? • Was fiercely resisted in Europe for hundreds of years after its discovery? • Even today, in historical treatments of mathematics, is often dismissed with scant mention, or else is ascribed to the wrong source? Answer: Our modern system of positional decimal notation with zero, to- gether with the basic arithmetic computational schemes, which were discov- ered in India prior to 500 CE. ∗Bailey: Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. Email: [email protected]. This work was supported by the Director, Office of Computational and Technology Research, Division of Mathematical, Information, and Computational Sciences of the U.S. Department of Energy, under contract number DE-AC02-05CH11231. yCentre for Computer Assisted Research Mathematics and its Applications (CARMA), University of Newcastle, Callaghan, NSW 2308, Australia. Email: [email protected]. 1 2 Why? As the 19th century mathematician Pierre-Simon Laplace explained: It is India that gave us the ingenious method of expressing all numbers by means of ten symbols, each symbol receiving a value of position as well as an absolute value; a profound and important idea which appears so simple to us now that we ignore its true merit. But its very sim- plicity and the great ease which it has lent to all computations put our arithmetic in the first rank of useful inventions; and we shall appre- ciate the grandeur of this achievement the more when we remember that it escaped the genius of Archimedes and Apollonius, two of the greatest men produced by antiquity.
    [Show full text]
  • Zero Displacement Ternary Number System: the Most Economical Way of Representing Numbers
    Revista de Ciências da Computação, Volume III, Ano III, 2008, nº3 Zero Displacement Ternary Number System: the most economical way of representing numbers Fernando Guilherme Silvano Lobo Pimentel , Bank of Portugal, Email: [email protected] Abstract This paper concerns the efficiency of number systems. Following the identification of the most economical conventional integer number system, from a solid criteria, an improvement to such system’s representation economy is proposed which combines the representation efficiency of positional number systems without 0 with the possibility of representing the number 0. A modification to base 3 without 0 makes it possible to obtain a new number system which, according to the identified optimization criteria, becomes the most economic among all integer ones. Key Words: Positional Number Systems, Efficiency, Zero Resumo Este artigo aborda a questão da eficiência de sistemas de números. Partindo da identificação da mais económica base inteira de números de acordo com um critério preestabelecido, propõe-se um melhoramento à economia de representação nessa mesma base através da combinação da eficiência de representação de sistemas de números posicionais sem o zero com a possibilidade de representar o número zero. Uma modificação à base 3 sem zero permite a obtenção de um novo sistema de números que, de acordo com o critério de optimização identificado, é o sistema de representação mais económico entre os sistemas de números inteiros. Palavras-Chave: Sistemas de Números Posicionais, Eficiência, Zero 1 Introduction Counting systems are an indispensable tool in Computing Science. For reasons that are both technological and user friendliness, the performance of information processing depends heavily on the adopted numbering system.
    [Show full text]
  • Maths Week 2021
    Maths Week 2021 Survivor Series/Kia Mōrehurehu Monday Level 5 Questions What to do for students 1 You can work with one or two others. Teams can be different each day. 2 Do the tasks and write any working you did, along with your answers, in the spaces provided (or where your teacher says). 3 Your teacher will tell you how you can get the answers to the questions and/or have your work checked. 4 When you have finished each day, your teacher will give you a word or words from a proverb. 5 At the end of the week, put the words together in the right order and you will be able to find the complete proverb! Your teacher may ask you to explain what the proverb means. 6 Good luck. Task 1 – numbers in te reo Māori The following chart gives numbers in te reo Māori. Look at the chart carefully and note the patterns in the way the names are built up from 10 onwards. Work out what each of the numbers in the following calculations is, do each calculation, and write the answer in te reo Māori. Question Answer (a) whitu + toru (b) whā x wa (c) tekau mā waru – rua (d) ono tekau ma whā + rua tekau ma iwa (e) toru tekau ma rua + waru x tekau mā ono Task 2 - Roman numerals The picture shows the Roman Emperor, Julius Caesar, who was born in the year 100 BC. (a) How many years ago was 100 BC? You may have seen places where numbers have been written in Roman numerals.
    [Show full text]
  • The What and Why of Whole Number Arithmetic: Foundational Ideas from History, Language and Societal Changes
    Portland State University PDXScholar Mathematics and Statistics Faculty Fariborz Maseeh Department of Mathematics Publications and Presentations and Statistics 3-2018 The What and Why of Whole Number Arithmetic: Foundational Ideas from History, Language and Societal Changes Xu Hu Sun University of Macau Christine Chambris Université de Cergy-Pontoise Judy Sayers Stockholm University Man Keung Siu University of Hong Kong Jason Cooper Weizmann Institute of Science SeeFollow next this page and for additional additional works authors at: https:/ /pdxscholar.library.pdx.edu/mth_fac Part of the Science and Mathematics Education Commons Let us know how access to this document benefits ou.y Citation Details Sun X.H. et al. (2018) The What and Why of Whole Number Arithmetic: Foundational Ideas from History, Language and Societal Changes. In: Bartolini Bussi M., Sun X. (eds) Building the Foundation: Whole Numbers in the Primary Grades. New ICMI Study Series. Springer, Cham This Book Chapter is brought to you for free and open access. It has been accepted for inclusion in Mathematics and Statistics Faculty Publications and Presentations by an authorized administrator of PDXScholar. Please contact us if we can make this document more accessible: [email protected]. Authors Xu Hu Sun, Christine Chambris, Judy Sayers, Man Keung Siu, Jason Cooper, Jean-Luc Dorier, Sarah Inés González de Lora Sued, Eva Thanheiser, Nadia Azrou, Lynn McGarvey, Catherine Houdement, and Lisser Rye Ejersbo This book chapter is available at PDXScholar: https://pdxscholar.library.pdx.edu/mth_fac/253 Chapter 5 The What and Why of Whole Number Arithmetic: Foundational Ideas from History, Language and Societal Changes Xu Hua Sun , Christine Chambris Judy Sayers, Man Keung Siu, Jason Cooper , Jean-Luc Dorier , Sarah Inés González de Lora Sued , Eva Thanheiser , Nadia Azrou , Lynn McGarvey , Catherine Houdement , and Lisser Rye Ejersbo 5.1 Introduction Mathematics learning and teaching are deeply embedded in history, language and culture (e.g.
    [Show full text]
  • Positional Notation Consider 101 1015 = ? Binary: Base 2
    1/21/2019 CS 362: Computer Design Positional Notation Lecture 3: Number System Review • The meaning of a digit depends on its position in a number. • A number, written as the sequence of digits dndn‐1…d2d1d0 in base b represents the value d * bn + d * bn‐1 + ... + d * b2 + d * b1 + d * b0 Cynthia Taylor n n‐1 2 1 0 University of Illinois at Chicago • For a base b, digits will range from 0 to b‐1 September 5th, 2017 Consider 101 1015 = ? • In base 10, it represents the number 101 (one A. 26 hundred one) = B. 51 • In base 2, 1012 = C. 126 • In base 8, 1018 = D. 130 101‐3=? Binary: Base 2 A. ‐10 • Used by computers B. 8 • A number, written as the sequence of digits dndn‐1…d2d1d0 where d is in {0,1}, represents C. 10 the value n n‐1 2 1 0 dn * 2 + dn‐1 * 2 + ... + d2 * 2 + d1 * 2 + d0 * 2 D. ‐30 1 1/21/2019 Binary to Decimal Decimal to Binary • Use polynomial expansion • Repeatedly divide by 2, recording the remainders. • The remainders form the binary digits of the number. 101102 = • Converting 25 to binary 3410=?2 Hexadecimal: Base 16 A. 010001 • Like binary, but shorter! • Each digit is a “nibble”, or half a byte • Indicated by prefacing number with 0x B. 010010 • A number, written as the sequence of digits dndn‐ C. 100010 1…d2d1d0 where d is in {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, represents the value D.
    [Show full text]
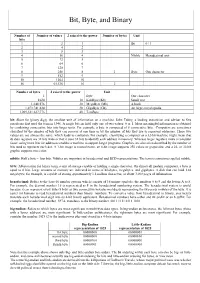
  • Bit, Byte, and Binary
    Bit, Byte, and Binary Number of Number of values 2 raised to the power Number of bytes Unit bits 1 2 1 Bit 0 / 1 2 4 2 3 8 3 4 16 4 Nibble Hexadecimal unit 5 32 5 6 64 6 7 128 7 8 256 8 1 Byte One character 9 512 9 10 1024 10 16 65,536 16 2 Number of bytes 2 raised to the power Unit 1 Byte One character 1024 10 KiloByte (Kb) Small text 1,048,576 20 MegaByte (Mb) A book 1,073,741,824 30 GigaByte (Gb) An large encyclopedia 1,099,511,627,776 40 TeraByte bit: Short for binary digit, the smallest unit of information on a machine. John Tukey, a leading statistician and adviser to five presidents first used the term in 1946. A single bit can hold only one of two values: 0 or 1. More meaningful information is obtained by combining consecutive bits into larger units. For example, a byte is composed of 8 consecutive bits. Computers are sometimes classified by the number of bits they can process at one time or by the number of bits they use to represent addresses. These two values are not always the same, which leads to confusion. For example, classifying a computer as a 32-bit machine might mean that its data registers are 32 bits wide or that it uses 32 bits to identify each address in memory. Whereas larger registers make a computer faster, using more bits for addresses enables a machine to support larger programs.
    [Show full text]
  • A Ternary Arithmetic and Logic
    Proceedings of the World Congress on Engineering 2010 Vol I WCE 2010, June 30 - July 2, 2010, London, U.K. A Ternary Arithmetic and Logic Ion Profeanu which supports radical ontological dualism between the two Abstract—This paper is only a chapter, not very detailed, of eternal principles, Good and Evil, which oppose each other a larger work aimed at developing a theoretical tool to in the course of history, in an endless confrontation. A key investigate first electromagnetic fields but not only that, (an element of Manichean doctrine is the non-omnipotence of imaginative researcher might use the same tool in very unusual the power of God, denying the infinite perfection of divinity areas of research) with the stated aim of providing a new perspective in understanding older or recent research in "free that has they say a dual nature, consisting of two equal but energy". I read somewhere that devices which generate "free opposite sides (Good-Bad). I confess that this kind of energy" works by laws and principles that can not be explained dualism, which I think is harmful, made me to seek another within the framework of classical physics, and that is why they numeral system and another logic by means of which I will are kept far away from public eye. So in the absence of an praise and bring honor owed to God's name; and because adequate theory to explain these phenomena, these devices can God is One Being in three personal dimensions (the Father, not reach the design tables of some plants in order to produce them in greater number.
    [Show full text]
  • Chapter 6 MISCELLANEOUS NUMBER BASES. the QUINARY
    The Number Concept: Its Origin and Development By Levi Leonard Conant Ph. D. Chapter 6 MISCELLANEOUS NUMBER BASES. THE QUINARY SYSTEM. The origin of the quinary mode of counting has been discussed with some fulness in a preceding chapter, and upon that question but little more need be said. It is the first of the natural systems. When the savage has finished his count of the fingers of a single hand, he has reached this natural number base. At this point he ceases to use simple numbers, and begins the process of compounding. By some one of the numerous methods illustrated in earlier chapters, he passes from 5 to 10, using here the fingers of his second hand. He now has two fives; and, just as we say “twenty,” i.e. two tens, he says “two hands,” “the second hand finished,” “all the fingers,” “the fingers of both hands,” “all the fingers come to an end,” or, much more rarely, “one man.” That is, he is, in one of the many ways at his command, saying “two fives.” At 15 he has “three hands” or “one foot”; and at 20 he pauses with “four hands,” “hands and feet,” “both feet,” “all the fingers of hands and feet,” “hands and feet finished,” or, more probably, “one man.” All these modes of expression are strictly natural, and all have been found in the number scales which were, and in many cases still are, in daily use among the uncivilized races of mankind. In its structure the quinary is the simplest, the most primitive, of the natural systems.
    [Show full text]
  • Number Systems and Number Representation Aarti Gupta
    Number Systems and Number Representation Aarti Gupta 1 For Your Amusement Question: Why do computer programmers confuse Christmas and Halloween? Answer: Because 25 Dec = 31 Oct -- http://www.electronicsweekly.com 2 Goals of this Lecture Help you learn (or refresh your memory) about: • The binary, hexadecimal, and octal number systems • Finite representation of unsigned integers • Finite representation of signed integers • Finite representation of rational numbers (if time) Why? • A power programmer must know number systems and data representation to fully understand C’s primitive data types Primitive values and the operations on them 3 Agenda Number Systems Finite representation of unsigned integers Finite representation of signed integers Finite representation of rational numbers (if time) 4 The Decimal Number System Name • “decem” (Latin) => ten Characteristics • Ten symbols • 0 1 2 3 4 5 6 7 8 9 • Positional • 2945 ≠ 2495 • 2945 = (2*103) + (9*102) + (4*101) + (5*100) (Most) people use the decimal number system Why? 5 The Binary Number System Name • “binarius” (Latin) => two Characteristics • Two symbols • 0 1 • Positional • 1010B ≠ 1100B Most (digital) computers use the binary number system Why? Terminology • Bit: a binary digit • Byte: (typically) 8 bits 6 Decimal-Binary Equivalence Decimal Binary Decimal Binary 0 0 16 10000 1 1 17 10001 2 10 18 10010 3 11 19 10011 4 100 20 10100 5 101 21 10101 6 110 22 10110 7 111 23 10111 8 1000 24 11000 9 1001 25 11001 10 1010 26 11010 11 1011 27 11011 12 1100 28 11100 13 1101 29 11101 14 1110 30 11110 15 1111 31 11111 ..
    [Show full text]
  • I – Mathematics in Design – SMTA1103
    SCHOOL OF SCIENCE AND HUMANITIES DEPARTMENT OF MATHEMATICS UNIT – I – Mathematics in Design – SMTA1103 UNIT1- MATHEMATICS IN DESIGN Golden Ratio The ratio of two parts of a line such that the longer part divided by the smaller part is also equal to the whole length divided by the longer part. Results: i) The ratio of the circumference of a circle to its diameter is π . ii) The ratio of the width of a rectangular picture frame to its height is not necessarily equal to he golden ratio, though some artists and architects believe a frame made using the golden ratio makes the most pleasing and beautiful shape.iii) The ratio of two successive numbers of the Fibonacci sequence give an approximate value of the golden ratio,the bigger the pair of Fibonacci Numbers, the closer the approximation. Example1: The Golden Ratio = 1.61803398874989484820... = 1.618 correct to 3 decimal places. If x n are terms of the Fibonacci sequence, then what is the least value of n for which ( x n +1 / x n = 1.618 correct to 3 decimal places. Example2: A rectangle divided into a square and a smaller rectangle. If (x + y) /y = x / y ,find the value of golden ratio. Example3: The Golden Ratio = 1.61803398874989484820... = 1.6180 correct to 4 decimal places. If xn are terms of the Fibonacci sequence, then what is the least value of n for which (x n +1) / x n = 1.618 0 correct to 4 decimal places. Example4: Obtain golden ratio in a line segment. Proportion Proportion is an equation which defines that the two given ratios are equivalent to each other.
    [Show full text]