DOCSLIB.ORG

Statistics with Jmp: Hypothesis Tests, Anova and Regression

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Statistics with Jmp: Hypothesis Tests, Anova and Regression STATISTICS WITH JMP: HYPOTHESIS TESTS, ANOVA AND REGRESSION PETER GOOS AND DAVID MEINTRUP STATISTICS WITH JMP: HYPOTHESIS TESTS, ANOVA AND REGRESSION STATISTICS WITH JMP HYPOTHESIS TESTS, ANOVA AND REGRESSION Peter Goos University of Leuven and University of Antwerp, Belgium David Meintrup University of Applied Sciences Ingolstadt, Germany This edition first published 2016 © 2016 John Wiley & Sons, Ltd Registered office John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, United Kingdom For details of our global editorial offices, for customer services and for information about how to apply for permission to reuse the copyright material in this book please see our website at www.wiley.com. The right of the authors to be identified as the authors of this work has been asserted in accordance withthe Copyright, Designs and Patents Act 1988. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, except as permitted by the UK Copyright, Designs and Patents Act 1988, without the prior permission of the publisher. Wiley also publishes its books in a variety of electronic formats. Some content that appears in print may not be available in electronic books. Designations used by companies to distinguish their products are often claimed as trademarks. All brand names and product names used in this book are trade names, service marks, trademarks or registered trademarks of their respective owners. The publisher is not associated with any product or vendor mentioned in this book. Limit of Liability/Disclaimer of Warranty: While the publisher and authors have used their best efforts in preparing this book, they make no representations or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose.Itis sold on the understanding that the publisher is not engaged in rendering professional services and neither the publisher nor the authors shall be liable for damages arising herefrom. If professional advice or other expert assistance is required, the services of a competent professional should be sought. Library of Congress Cataloging-in-Publication Data Names: Goos, Peter. | Meintrup, David. Title: Statistics with JMP : hypothesis tests, ANOVA, and regression / Peter Goos, David Meintrup. Description: Chichester, West Sussex : John Wiley & Sons, Inc., 2016. | Includes index. Identifiers: LCCN 2015039990 (print) | LCCN 2015047679 (ebook) | ISBN 9781119097150 (cloth)| ISBN 9781119097044 (Adobe PDF) | ISBN 9781119097167 (ePub) Subjects: LCSH: Probabilities–Data processing. | Mathematical statistics–Data processing. | Regression analysis. | JMP (Computer file) Classification: LCC QA273.19.E4 G68 2016 (print) | LCC QA273.19.E4 (ebook)| DDC 519.50285/53–dc23 LC record available at http://lccn.loc.gov/2015039990 A catalogue record for this book is available from the British Library. Set in 10/12pt Times by Aptara Inc., New Delhi, India 1 2016 To Marijke, Bas, Loes, and Mien To Beatrice´ and Werner Contents Preface xv Acknowledgments xix Part One ESTIMATORS AND TESTS 1 1 Estimating Population Parameters 3 1.1 Introduction: Estimators Versus Estimates 3 1.2 Estimating a Mean Value 4 1.2.1 The Mean of a Normally Distributed Population 4 1.2.2 The Mean of an Exponentially Distributed Population 6 1.3 Criteria for Estimators 6 1.3.1 Unbiased Estimators 8 1.3.2 The Efficiency of an Estimator 9 1.4 Methods for the Calculation of Estimators 9 1.5 The Sample Mean 10 1.5.1 The Expected Value and the Variance 10 1.5.2 The Probability Density of the Sample Mean for a Normally Distributed Population 12 1.5.3 The Probability Density of the Sample Mean for a Nonnormally Distributed Population 12 1.5.4 An Illustration of the Central Limit Theorem 14 1.6 The Sample Proportion 18 1.7 The Sample Variance 21 1.7.1 The Expected Value 22 1.7.2 The 2-Distribution 24 1.7.3 The Relation Between the Standard Normal and the 2-Distribution 25 1.7.4 The Probability Density of the Sample Variance 28 1.8 The Sample Standard Deviation 30 1.9 Applications 33 2 Interval Estimators 35 2.1 Point and Interval Estimators 35 viii Contents 2.2 Confidence Intervals for a Population Mean with Known Variance 36 2.2.1 The Percentiles of the Standard Normal Density 36 2.2.2 Computing a Confidence Interval 38 2.2.3 The Width of a Confidence Interval 39 2.2.4 The Margin of Error 41 2.3 Confidence Intervals for a Population Mean with Unknown Variance 41 2.3.1 The Student t-Distribution 42 2.3.2 The Application of the t-Distribution to Construct Confidence Intervals 45 2.4 Confidence Intervals for a Population Proportion 47 2.4.1 A First Interval Estimator Based on the Normal Distribution 47 2.4.2 A Second Interval Estimator Based on the Normal Distribution 49 2.4.3 An Interval Estimator Based on the Binomial Distribution 50 2.5 Confidence Intervals for a Population Variance 52 2.6 More Confidence Intervals in JMP 56 2.7 Determining the Sample Size 58 2.7.1 The Population Mean 60 2.7.2 The Population Proportion 63 3 Hypothesis Tests 67 3.1 Key Concepts 67 3.2 Testing Hypotheses About a Population Mean 71 3.2.1 The Right-Tailed Test 71 3.2.2 The Left-Tailed Test 77 3.2.3 The Two-Tailed Test 78 3.3 The Probability of a Type II Error and the Power 85 3.4 Determination of the Sample Size 88 3.5 JMP 90 3.6 Some Important Notes Concerning Hypothesis Testing 93 3.6.1 Fixing the Significance Level 94 3.6.2 A Note on the “Acceptance” of the Null Hypothesis 95 3.6.3 Statistical and Practical Significance 95 Part Two ONE POPULATION 97 4 Hypothesis Tests for a Population Mean, Proportion, or Variance 99 4.1 Hypothesis Tests for One Population Mean 99 4.1.1 The Right-Tailed Test 100 4.1.2 The Left-Tailed Test 102 4.1.3 The Two-Tailed Test 102 4.1.4 Nonnormal Data 107 4.1.5 The Use of JMP 108 4.2 Hypothesis Tests for a Population Proportion 110 4.2.1 Tests Based on the Normal Distribution 111 4.2.2 Tests Based on the Binomial Distribution 117 4.2.3 Testing Proportions in JMP 119 Contents ix 4.3 Hypothesis Tests for a Population Variance 122 4.3.1 The Right-Tailed Test 123 4.3.2 The Left-Tailed Test 124 4.3.3 The Two-Tailed Test 125 4.3.4 The Use of JMP 127 4.4 The Probability of a Type II Error and the Power 128 4.4.1 Tests for a Population Mean 130 4.4.2 Tests for a Population Proportion 140 4.4.3 Tests for a Population Variance and Standard Deviation 141 5 Two Hypothesis Tests for the Median of a Population 143 5.1 The Sign Test 144 5.1.1 The Starting Point of the Sign Test 145 5.1.2 Exact p-Values 147 5.1.3 Approximate p-Values Based on the Normal Distribution 148 5.2 The Wilcoxon Signed-Rank Test 151 5.2.1 The Use of Ranks 151 5.2.2 The Starting Point of the Signed-Rank Test 152 5.2.3 Exact p-Values 155 5.2.4 Exact p-Values for Ties 160 5.2.5 Approximate p-Values Based on the Normal Distribution 162 5.2.6 Approximate p-Values Based on the t-Distribution 164 6 Hypothesis Tests for the Distribution of a Population 167 6.1 Testing Probability Distributions 167 6.1.1 Known Parameters 168 6.1.2 Unknown Parameters 170 6.1.3 2-Tests for Qualitative Variables 172 6.2 Testing Probability Densities 181 6.2.1 The Normal Probability Density 182 6.2.2 Other Continuous Densities 195 6.3 Discussion 196 Part Three TWO POPULATIONS 199 7 Independent Versus Paired Samples 201 8 Hypothesis Tests for the Means, Proportions, or Variances of Two Independent Samples 205 8.1 Tests for Two Population Means for Independent Samples 205 8.1.1 The Starting Point 206 2 2 8.1.2 Known Variances 1 and 2 207 2 2 8.1.3 Unknown Variances 1 and 2 212 8.1.4 Confidence Intervals for a Difference in Population Means 222 8.2 A Hypothesis Test for Two Population Proportions 224 x Contents 8.2.1 The Starting Point 225 8.2.2 The Right-Tailed Test 226 8.2.3 The Left-Tailed Test 226 8.2.4 The Two-Tailed Test 226 8.2.5 Generalized Hypothesis Tests 227 8.2.6 The Confidence Interval for a Difference in Population Proportions 228 8.3 A Hypothesis Test for Two Population Variances 229 8.3.1 Fisher’s F-Distribution 230 8.3.2 The F-Test for the Comparison of Two Population Variances 232 8.3.3 The Confidence Interval for a Quotient of Two Population Variances 237 8.4 Hypothesis Tests for Two Independent Samples in JMP 237 8.4.1 Two Population Means 237 8.4.2 Two Population Proportions 244 8.4.3 Two Population Variances 247 9 A Nonparametric Hypothesis Test for the Medians of Two Independent Samples 251 9.1 The Hypotheses Tested 252 9.1.1 The Procedure 252 9.1.2 The Starting Point 253 9.2 Exact p-Values in the Absence of Ties 254 9.2.1 The Right-Tailed Test 256 9.2.2 The Left-Tailed Test 257 9.2.3 The Two-Tailed Test 261 9.3 Exact p-Values in the Presence of Ties 261 9.4 Approximate p-Values 265 9.4.1 The Right-Tailed Test 265 9.4.2 The Left-Tailed Test 266 9.4.3 The Two-Tailed Test 267 10 Hypothesis Tests for the Means of Two Paired Samples 273 10.1 The Hypotheses Tested 273 10.2 The Procedure 274 10.2.1 The Starting Point 274 10.2.2 Known D 277 10.2.3 Unknown D 278 10.3 Examples 280 10.4 The Technical Background 288 10.5 Generalized Hypothesis Tests 289 10.6 A Confidence Interval for a Difference of Two Population Means 290 10.6.1 Known D 290 10.6.2 Unknown D 291 11 Two Nonparametric Hypothesis Tests for Paired Samples 293 11.1 The Sign Test 294 11.1.1 The Hypotheses Tested 294 Contents xi 11.1.2 Practical Implementation 295 11.1.3 JMP 300 11.2
Load more

Recommended publications
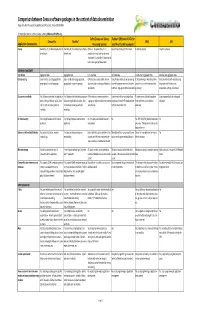
  • Comparison Between Census Software Packages in the Context of Data Dissemination Prepared by Devinfo Support Group (DSG) and UN Statistics Division (DESA/UNSD)
    Comparison between Census software packages in the context of data dissemination Prepared by DevInfo Support Group (DSG) and UN Statistics Division (DESA/UNSD) For more information or comments please contact: [email protected] CsPro (Census and Survey Redatam (REtrieval of DATa for CensusInfo DevInfo* SPSS SAS Application Characteristics Processing System) small Areas by Microcomputer) License Owned by UN, distributed royalty-free to Owned by UN, distributed royalty-free to CSPro is in the public domain. It is Version free of charge for Download Properitery license Properitery license all end-users all end-users available at no cost and may be freely distributed. It is available for download at www.census.gov/ipc/www/cspro DATABASE MANAGEMENT Type of data Aggregated data. Aggregated data. Individual data. Individual data. Individual and aggregated data. Individual and aggregated data. Data processing Easily handles data disaggregated by Easily handles data disaggregated by CSPro lets you create, modify, and run Using Process module allows processing It allows entering primary data, define It lets you interact with your data using geographical area and subgroups. geographical area and subgroups. data entry, batch editing, and tabulation data with programs written in Redatam variables and perform statistical data integrated tools for data entry, applications command language or limited Assisstants processing computation, editing, and retrieval. Data consistency checks Yes, Database administration application Yes, Database administration
    [Show full text]
  • Research; *Electronic Data Processing; Information Processing; Information Systems; *Manpower Utilization; *Personnel Data; Personnel Management; Questionnaires
    DOCUMENT RESUME ED 084 382 CE 000 533 AUTHOR Bayhylle, J. E., Ed.; Hersleb, A., Ed. TITLE The Development of Electronic Data Processing in Manpower Areas; A Comparative Study of Personnel Information Systems and their Implications in Six European Countries. INSTITUTION Organisation for Economic Cooperation and Development, Paris (France) . PUB DATE 73 NOTE 366p. AVAILABLE FROMOECD Publications Center, Suite 1207, 1750 Pennsylvania Ave., N.W., Washington, DC 20006 ($8.50) EDRS PRICE MF-$0.65 HC- $13.16 DESCRIPTORS Case Studies; Data Bases; Data Processing; *Ecqnomic .Research; *Electronic Data Processing; Information Processing; Information Systems; *Manpower Utilization; *Personnel Data; Personnel Management; Questionnaires ABSTRACT Usable data about human resources in the ecqnqmy are fundamentally important, but present methods of obtaining, organizing, and using such information are increasingly unsatisfactory. The application of electronic data processing to manpower and social concerns should be improved and increased. This could stimulate closer exchange between government, institutions, and business enterprises in the collection and dissemination of manpower data. The first phase of the study was a broad-scope questionnaire of 38 companies in Austria, France, Germany, Great Britain, Sweden, and Switzerland which have developed, or are planning to develop, computer-based personnel information, systems. The second phase consisted of depth study of eight of the companies. Case study investigations were concerned with the content and function of the system and with the administrative and personnel consequences of the introduction of such systems. A set of key.points which emerged from the study is developed. A model demonstrates the need for coordination to increase communication vertically and horizontally.
    [Show full text]
  • Applied Accounting and Automatic Data-Processing Systems." (1962)
    Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1962 Applied Accounting and Automatic Data- Processing Systems. William Elwood Swyers Louisiana State University and Agricultural & Mechanical College Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_disstheses Recommended Citation Swyers, William Elwood, "Applied Accounting and Automatic Data-Processing Systems." (1962). LSU Historical Dissertations and Theses. 745. https://digitalcommons.lsu.edu/gradschool_disstheses/745 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Historical Dissertations and Theses by an authorized administrator of LSU Digital Commons. For more information, please contact [email protected]. This dissertation has been 62—3671 microfilmed exactly as received SWYERS, William Elwood, 1922- APPLIED ACCOUNTING AND AUTOMATIC DATA-PRO CESSING SYSTEMS. Louisiana State University, Ph.D., 1962 Economics, commerce—business University Microfilms, Inc., Ann Arbor, Michigan APPLIED ACCOUNTING AND AUTOMATIC DATA-PROCESSING SYSTEMS A Dissertation Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College in partial fulfillment of the requirements for the degree of Doctor of Philosophy in The Department of Accounting by William Eiu<Swyers B.S., Centenary College, 1942 M.B.A. t Louisiana State University, 1948 January, 1962 ACKNOWLEDGMENTS The writer wishes to express appreciation to Dr. Robert H. Van Voorhis, Professor of Accounting, Louisiana State University, for his valuable assistance and guidance in the preparation of this dissertation. The writer wishes to acknowledge, also, the helpful suggestions made by Dr. W. D. Ross, Dean of the College of Business Administration, Dr.
    [Show full text]
  • STANDARDS and GUIDELINES for STATISTICAL SURVEYS September 2006
    OFFICE OF MANAGEMENT AND BUDGET STANDARDS AND GUIDELINES FOR STATISTICAL SURVEYS September 2006 Table of Contents LIST OF STANDARDS FOR STATISTICAL SURVEYS ....................................................... i INTRODUCTION......................................................................................................................... 1 SECTION 1 DEVELOPMENT OF CONCEPTS, METHODS, AND DESIGN .................. 5 Section 1.1 Survey Planning..................................................................................................... 5 Section 1.2 Survey Design........................................................................................................ 7 Section 1.3 Survey Response Rates.......................................................................................... 8 Section 1.4 Pretesting Survey Systems..................................................................................... 9 SECTION 2 COLLECTION OF DATA................................................................................... 9 Section 2.1 Developing Sampling Frames................................................................................ 9 Section 2.2 Required Notifications to Potential Survey Respondents.................................... 10 Section 2.3 Data Collection Methodology.............................................................................. 11 SECTION 3 PROCESSING AND EDITING OF DATA...................................................... 13 Section 3.1 Data Editing ........................................................................................................
    [Show full text]
  • What Can a Computer Do? a Computer Is an Electronic Device
    You have learnt various methods of data processing and representation that you can use to analyse the geographical phenomena in the preceding chapters. You must have observed that these methods are time consuming and tedious. Have you ever thought of a method of data processing and their graphical representation that can save time and improve efficiency? If you have used a computer for word processing, then you must have noticed that the computer is more versatile as it facilitates the onscreen editing of the text, copy and move it from one place to another, or even delete the unwanted text. Similarly, the computer may also be used for data processing, preparation of diagrams/graphs and drawing of maps, provided you have an access to the related application software. In other words, a computer can be used for a wide range of applications. It must, however, be clearly understood that a computer carries out the instructions it receives from the users. In other words, it cannot perform any function on its own. In the present chapter, we will discuss the use of computers in data processing and mapping. What can a Computer do? A computer is an electronic device. It consists of various sub-systems, like memory, micro-processor, input system and output system. All these sub- systems work together to make it an integrated system. It is an extremely powerful device, which is apt to have an important effect on the systems of data processing, mapping and analysis. A computer is a fast and a versatile machine that can perform simple arithmetic operations, such as, addition, subtraction, multiplication and division, and can also solve complex mathematical, formulae.
    [Show full text]
  • 14. Data Processing, Evaluation, and Analysis
    In: R.P. Higgins & H. 'I'hi,el (Eds.) Introduction to the study of Meiofauna. ~vashington and London', Sml't11sonian Institution Press, 1988, pp. 197-231. Communication no. 418 Delta Institute for Hydrobiological Research, Vierstraat 28 Yerseke, The Netherlands. 14. Data Processing, Evaluation, and Analysis Carlo Heip, Peter M.J. Herman, and Karlien Soetaert This chapter aims at introducing a number of and evenness indices in part 5, and temporal pattern methods for the post-hoc interpretation of field in part 6. Each of these topics is discussed data. In many ecological studies a vast amount of independently and each topic can be consulted information is gathered, often in the form of without having to read the others. For this reason, numbers of different species. The processing of these each part will be preceded by its own introduction. data is possible on different levels of sophistication and requires the use of tools varying from pencil Part 1. Data Storage and Retrieval and paper to a mini computer. However, some "number crunching" is nearly always necessary and The existence of many software packages, useful with the increasing availability and decreasing prices in ecology, will not be unknown to most ecologists. ,of the personal computer, even in developing Many computer centers provide their users with countries, there is little point in avoiding the more routines which facilitate the input, transformation and advanced statistical techniques. There is also a more appropriate output of the data, and the linking of fundamental reason: ecological data are often of a available software packages into one flexible system.
    [Show full text]
  • Course Title: Fundermentals of Data Processing
    NATIONAL OPEN UNIVERSITY OF NIGERIA SCHOOL OF EDUCATION COURSE CODE: BED 212: COURSE TITLE: FUNDERMENTALS OF DATA PROCESSING BED 212: FUNDERMENTALS OF DATA PROCESSING COURSE DEVELOPER & WRITER: DR. OPATEYE JOHNSON AYODELE School of Education National Open University of Nigeria 14/16 Ahmadu Bello Way, Victoria Island Lagos. Nigeria. COURSE CORDINATOR: DR. INEGBEDION, JULIET O. School of Education National Open University of Nigeria 14/16 Ahmadu Bello Way, Victoria Island Lagos. Nigeria. INTRODUCTION BED 212: FUNDERMENTALS OF DATA PROCESSING This course is designed to equip the students with knowledge of the data processing in technical and vocational education (TVE) especially Business Education research. WHAT YOU WILL LEARN You will learn the components of data processing, hardware and software components, file management and organization in Business Education- based data. It will also interest you to learn about basics of research, approaches and designs with data gathering techniques. Relevant statistical tools you can use to analyse your data would be across and how to write your research reports. COURSE AIMS This course aims at producing competent business educators who will be versed in organizational and research data processing in order to foster time and effective information that will be used in decision making. In order to enable you meet the above aims, modules constituting of units have been produced for your study. Apart from meeting the aims of the course as a whole, each course unit consists of learning objectives which are intended to ensure your learning effectiveness. COURSE OBJECTIVES The course objectives are meant to enable you achieve/acquire the following: 1) Gain in-depth knowledge of data processing and its functions in business organisations and educational settings.
    [Show full text]
  • Hyperspectral Data Processing. Algorithm Design and Analysis
    Brochure More information from http://www.researchandmarkets.com/reports/2293144/ Hyperspectral Data Processing. Algorithm Design and Analysis Description: Hyperspectral Data Processing: Algorithm Design and Analysis is a culmination of the research conducted in the Remote Sensing Signal and Image Processing Laboratory (RSSIPL) at the University of Maryland, Baltimore County. Specifically, it treats hyperspectral image processing and hyperspectral signal processing as separate subjects in two different categories. Most materials covered in this book can be used in conjunction with the author’s first book, Hyperspectral Imaging: Techniques for Spectral Detection and Classification, without much overlap. Many results in this book are either new or have not been explored, presented, or published in the public domain. These include various aspects of endmember extraction, unsupervised linear spectral mixture analysis, hyperspectral information compression, hyperspectral signal coding and characterization, as well as applications to conceal target detection, multispectral imaging, and magnetic resonance imaging. Hyperspectral Data Processing contains eight major sections: - Part I: provides fundamentals of hyperspectral data processing - Part II: offers various algorithm designs for endmember extraction - Part III: derives theory for supervised linear spectral mixture analysis - Part IV: designs unsupervised methods for hyperspectral image analysis - Part V: explores new concepts on hyperspectral information compression - Parts VI & VII: develops
    [Show full text]
  • Cit 213 Course Title: Elementary Data Processing
    NATIONAL OP EN UNIVERSITY OF NIGERIA SCHOOL OF SCIENCE AND TECHNOLOGY COURSE CODE: CIT 213 COURSE TITLE: ELEMENTARY DATA PROCESSING CO URSE GUIDE CIT 213 ELEMENTARY DATA PROCESSING Course Developer Dr. Ikhu-Omoregbe N. A. Course Editor Course Co-ordinator Afolorunso, A. A. National Open University of Nigeria Lagos. NATIONAL OPEN UNIVERSITY OF NIGERIA National Open University of Nigeria Headquarters 14/16 Ahmadu Bello Way Victoria Island Lagos Abuja Annex 245 Samuel Adesujo Ademulegun Street Central Business District Opposite Arewa Suites Abuja e-mail: [email protected] URL: www.nou.edu.ng National Open University of Nigeria 2008 First Printed 2008 ISBN All Rights Reserved Printed by .. For National Open University of Nigeria TABLE OF CONTENTS PAGE Introduction.............................................................................. 1 - 2 What you will learn in this Course..................................... 2 Course Aims............................................................................... 2 Course Objectives...................................................................... 2 3 Working through this Course.................................................... 3 Course Materials...........................................................................3 Study Units ............................................................................... 3 - 4 Textbooks and References ........................................................ 4 - 5 Assignment File.......................................................................
    [Show full text]
  • Data Processing Operations Technician
    Fremont Unified School District Classified Job Description Office and Technical DATA PROCESSING OPERATIONS TECHNICIAN DEFINITION Under general supervision, assists in the day-to-day operation of the Management Information Systems Department; assists users with centralized MIS and/or help desk requests; operates electronic computer and peripheral equipment; and performs related work as assigned. CLASS CHARACTERISTICS This class provides a variety of technical assistance to the Management Information Systems Department, in the areas of tracking and processing mainframe operations jobs and in providing technical assistance to users in various District offices and school sites. This class is distinguished from Computer Operator/Programmer in that the latter performs programming activities in addition to batch and on-line operations within the MIS centralized operations center. EXAMPLES OF DUTIES Receives users requests; determines the appropriate staff to fulfill the request and processes required paperwork; refers special requests to programmers or other technical staff. Schedules batch jobs, ensures and tracks proper sequence to meet established deadlines and user needs. Operates the mainframe console and peripheral equipment to run batch jobs and/or initiates command files for later execution. Obtains printouts of reports to be distributed. Loads appropriate forms and paper styles on line printers. Prepares tapes for microfiche or other long-term storage; calls for pick-up, files and distributes when returned. Maintains database elements, ensuring continuing validity. Assists Operations Supervisor in evaluating operation of the computer and related equipment and in maintaining the system communication scheme. Provides information and assistance to system-users, facilitating on-line applications. In event of malfunction, resets the current operation or contacts appropriate District or vendor support staff as required.
    [Show full text]
  • An Analysis of Information Technology on Data Processing by Using Cobit Framework
    (IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 6, No. 9, 2015 An Analysis of Information Technology on Data Processing by using Cobit Framework Surni Erniwati Nina Kurnia Hikmawati Academy of Information Management and Computer Telkom University Bandung AMIKOM Mataram Universitas Telkom Bandung Mataram, Indonesia Bandung, Indonesian Abstract—Information technology and processes is inter administrative services and academic information quickly and connected, directing and controlling the company in achieving accurately. ABASA already supported by IT in data corporate goals through value-added and balancing the risks and processing, which for the procurement of IT is implemented by benefits of information technology. This study is aimed to analyze a separate division, namely division BPSI. However, research the level of maturity (maturity level) on the data process and has not been done to measure the maturity level data produced information technology recommendations that can be processing and mapping the information technology process made as regards the management of IT to support the academic maturity level of the institution cannot be measured, in addition performance of the service to be better. Maturity level to these problems relating to data processing, how to maintain calculation was done by analyzing questionnaires on the state of the completeness, accuracy and availability of data through the information technology. The results of this study obtainable that efforts of data backup, data storage or deletion of data. Based the governance of information technology in data processing in Mataram ASM currently quite good. Current maturity value for on those problems, this study is aimed to make a the data processing has the value 2.69.
    [Show full text]
  • Processing the Data
    CHAPTER 7 PROCESSING THE DATA This chapter is written for survey coordinators, data processing experts and technical resource persons. It provides information on how to: Prepare for processing the data Set up a system for managing data processing Carry out data entry Edit the data and create a ‘clean’ data file for analysis Produce tabulations with the indicators Archive and distribute data The MICS3 data-processing system is designed to deliver the first results of a survey within a few weeks after the end of fieldwork. This chapter contains information that will help you to undertake the planning and advance preparation that will make this goal a reality. The chapter begins by giving you an overview of the MICS3 data-processing system. It then discusses each of its components in detail, providing references to supplemental sources of information where appropriate. It closes with a set of three checklists that will help you make the processing of your survey data a success. OVERVIEW The reason that the MICS3 data-processing system can achieve such rapid turnaround time is because data is processed in tandem with survey fieldwork. Data for each cluster is stored in a separate data file and is processed as soon as the questionnaires are returned from the field. This approach breaks data processing down into discrete segments and allows it to progress while fieldwork is ongoing. Thus, by the time the last questionnaires are finished and returned to headquarters, most of the data have already been processed. Processing the data by clusters is not difficult, but it does require meticulous organization.
    [Show full text]