Development of an Inverse Design Method for Propellers with Application on Left Ventricular Assist Devices
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

PTC Creo® Parametric™
Data Sheet PTC Creo® Parametric™ The Essential 3D Parametric CAD Solution PTC Creo Parametric gives you exactly what you need: The most robust, scalable 3D product design toolset with more power, flexibility, and speed to help you accelerate your entire product development process. Where breakthrough products begin Key benefits PTC Creo Parametric is a scalable, interoperable • Increase productivity with more efficient and parametric solution for maximizing innovation, flexible 3D detailed design capabilities improving quality in 3D product design, and delivering faster time to value. The software helps you quickly • Quickly and easily create 3D models of any part deliver the most accurate digital models with the or assembly highest quality. In addition, high-fidelity digital models have full associativity so that product changes made • Dedicated toolset for working with large assemblies anywhere can update deliverables everywhere. That’s what it takes to achieve the digital product confidence • Create manufacturing drawings automatically needed before investing significant capital in sourcing, with complete confidence that they will always manufacturing capacity, and volume production. With reflect your current design a comprehensive library of CAD, CAID, CAM, and CAE extensions, PTC Creo Parametric has the ability to • Improve design aesthetics with comprehensive grow as your business and product development surfacing capabilities needs grow. • Repurpose neutral and non PTC CAD data from customers and suppliers easily, avoiding the need to convert files or recreate 3D models from scratch • Instant access to a parts library including screws, bolts, nuts, and washers • Get instant access to comprehensive learning materials and tutorials from within the product to get productive faster Create High Quality 3D models of your product designs. -

PTC Creo® Parametric
Data Sheet PTC Creo® Parametric THE ESSENTIAL 3D PARAMETRIC CAD SOLUTION PTC Creo Parametric gives you exactly what you need: the most robust, scalable 3D product design toolset with more power, flexibility and speed to help you accelerate your entire product development process. Where breakthrough products begin • Increase productivity with more efficient and flexible 3D detailed design capabilities Engineering departments face countless challenges • Increase model quality, promote native and as they strive to create breakthrough products. They multi-CAD part reuse, and reduce model errors must manage exacting technical processes, as well as the rapid flow of information across diverse • Handle complex surfacing requirements with ease development teams. In the past, companies seeking • Instantly connect to information and resources on CAD benefits could opt for tools that focused on the Internet – for a highly efficient product ease-of-use, yet lacked depth and process breadth. Or, development process they could choose broader solutions that fell short on usability. With PTC Creo Parametric, companies get The superior choice for speed-to-value both a simple and powerful solution, to create great products without compromise. Through its flexible workflow and sleek user interface, PTC Creo Parametric drives personal engineering PTC Creo Parametric, helps you quickly deliver the productivity like no other 3D CAD software. The highest quality, most accurate digital models. With industry-leading user experience enables direct its seamless Web connectivity, it provides product modeling, provides feature handles and intelligent teams with access to the resources, information snapping, and uses geometry previews, so users can and capabilities they need – from conceptual design see the effects of changes before committing to them. -
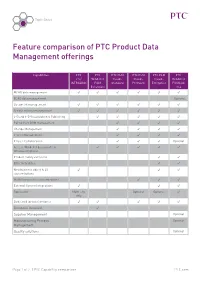
Feature Comparison of PTC Product Data Management Offerings
Topic Sheet Feature comparison of PTC Product Data Management offerings Capabilities PTC PTC PTC PLM PTC PLM PTC PLM PTC Pro/ Windchill Cloud - Cloud - Cloud - Windchill INTRALINK PDM Standard Premium Enterprise PDMLink Essentials 10.2 MCAD data management ECAD data management Optional Document management Simple release management 2-D and 3-D Visualization & Publishing Part & Part BOM management Change Management Project Management Project Collaboration Optional Access Windchill documents in Windows Explorer Product family variations Effectivity dates New business object & UI customizations Workflow process customizations External System Integrations Replication Multi-site Optional Optional only Dedicated (private) instance Database included Supplier Management Optional Manufacturing Process Optional Management Quality solutions Optional Page 1 of 2 | PTC Capability comparison PTC.com Topic Sheet CAD Integrations PTC PTC PTC PLM PTC PLM PTC PLM PTC Pro/ Windchill Cloud - Cloud - Cloud - Windchill INTRALINK PDM Standard Premium Enterprise PDMLink Essentials 10.2 PTC Creo AutoCAD SolidWorks Autodesk Inventor NX Optional CATIA V5 Optional ECAD Optional Licensing License category Floating Floating Active Active Active Registered License types Heavy/ Only one Author/ Author/ Author/ Heavy/ Light/View license type Viewer Contributor/ Contributor/ Light/View & Print Viewer Viewer & Print Subscription or on-premise Both On-premise Subscription Subscription Subscription Both Deployment Server location On-premise On-premise Cloud Cloud Cloud On-premise or cloud or cloud Managed by PTC Cloud Services Optional No Yes Yes Yes Optional © 2015, PTC Inc. All rights reserved. Information described herein is furnished for informational use only, is subject to change without notice, and should not be taken as a guarantee, commitment, condition or offer by PTC. -

PTC Creo® Simulate
Data Sheet PTC Creo® Simulate PTC Creo Simulate gives designers and engineers the power to evaluate structural and thermal product performance on your digital model before resorting to costly, time-consuming physical prototyping. By gaining early insight into product behavior, you can greatly improve product quality while saving time, effort and money. The software has the same user interface, workflow ɒ FEM mode: Use of ANSYS solver and productivity tools that are standard throughout - Linear Static Structural Analysis the PTC Creo family. It is available as a standalone application or as an extension of PTC Creo Parametric. - Modal Structural Analysis Features and Specifications - Linear Steady State Thermal Analysis ɒ Fatigue (optional module) Analysis Capabilities ɒ Linear Static Structural Analysis ɒ Static Structural Analysis with Small Displacement Contact ɒ Modal Structural Analysis ɒ Linear Buckling Structural Analysis ɒ Linear Steady State Thermal Analysis ɒ FEM mode: Use of NASTRAN solver - Linear Static Structural Analysis - Modal Structural Analysis You can analyze your model and quickly identify problem areas. Once you update the design, you can easily rerun the analysis, without recreating it. Page 1 of 5 | PTC Creo Simulate PTC.com Data Sheet Convergence ɒ Material Library ɒ P-type Finite Element methodology - Typical metals and plastics included ɒ Single Pass Adaptive - Storage of user defined materials ɒ Multi-Pass Adaptive - Departmental or company material libraries ɒ User control on convergence criteria ɒ Coordinate -

PTC® Creo® Essentials Packages Powerful 3D CAD Solutions Optimized for Your Product Development Tasks
PTC Creo Essentials Packages PTC® CREO® ESSENTIALS PACKAGES Powerful 3D CAD solutions optimized for your product development tasks Product design firms and manufacturing companies are of your specific engineering design tasks and business under constant pressure to develop more products in less requirements as you grow. time, without sacrificing innovation or quality. No matter which package you choose, users will be able PTC’s 3D product design solution, PTC Creo, provides to take advantage of a powerful, intuitive, and comprehen- engineers with the right tools to achieve the highest qual- sive set of 3D CAD capabilities. ity designs in the fastest possible time. And since it is an integral part of PTC’s Product Develop- PTC delivers the most scalable range of 3D CAD product ment System, your 3D CAD solution will seamlessly development packages on the market today. Available connect to PTC’s other industry-leading solutions, including exclusively through PTC Value Added Resellers, the PTC PTC Windchill® for product data/product lifecycle Creo Essentials Packages are easy to use, competitively management (PDM/PLM) and PTC Mathcad® for priced and always upgradeable–to meet the varied needs engineering calculations. Page 1 of 7 PTC.com PTC Creo Essentials Packages PTC Creo Essentials Packages - At a Glance 3D Part & Assembly Design................................................................................... Automated 2D Drawing Creation & Update..................................................... Breakthrough multi-CAD data exchange -

NVIDIA WORKSTATION Gpus NVIDIA PROFESSIONAL SOLUTION GUIDE
THE RIGHT TOOLS FOR PROFESSIONALS NVIDIA WORKSTATION GPUs NVIDIA PROFESSIONAL SOLUTION GUIDE Find the best professional solution for your customers based on their needs The current NVIDIA® RTX™ lineup includes NVIDIA Volta™, Turing™, and Ampere architectures. Please request that your customers contact their software providers for the latest information on application certifications and support. ASK > Are you a technical professional? 1 > Is your title: designer, engineer, architect, scientist, analyst, data scientist or researcher? > Do you create, render or visualize large data and images for your work? > Do you train or use neural networks? > Do you use computationally intensive applications or run simulations? YES NO You have found an NVIDIA RTX Customer Go to page 6 for display and video wall recommendations for other industries 2 > What industry do you work in or what is your job? and professionals. > What is the primary application you use? GOOD BETTER BEST 3 > Occasional use of application > Regular use of application > Pushing the application to its limits > Small objects and assemblies > Average to large objects and > Extremely large objects and > About 10% of the users assemblies assemblies > Using all application features > Using all application features > About 80% of users > About 10% of users DESIGN/ENGINEERING/MANUFACTURING Altair® HyperWorks® NVIDIA RTX A4000 NVIDIA RTX A5000 NVIDIA RTX A6000 Altair AcuSolve® NVIDIA RTX A5000 Quadro RTX 8000 NVIDIA RTX A6000 Altair ultraFluidX®, 2x NVIDIA RTX A6000 4x NVIDIA RTX A6000 -

Top Enhancements in PTC Creo® Parametric™ 3.0
Data Sheet Extension Top Enhancements in PTC Creo® Parametric™ 3.0 The Essential 3D Parametric CAD Solution PTC Creo Parametric, PTC’s 3D parametric modeling system, provides the broadest range of powerful yet flexible 3D CAD capa- bilities to help you address your most pressing design challenges. It uses proven technologies from Pro/ENGINEER®, plus hundreds of new capabilities to unlock design productivity. Here are some of the top enhancements in PTC Creo Parametric 3.0. Unparalleled multi-CAD data handling capabilities As well as being able to import neutral file formats (e.g., STEP, IGES, DXF, etc.) directly into PTC Creo Parametric, users can now both import and open CATIA®, SolidWorks®, and Siemens® NX TM files without the need for a separate translator or access to the native authoring software. With the addition of collaboration extensions, users can also collaborate with non-native PTC Creo software and receive automatic updates of geometry TM changes from CATIA®, SolidWorks TM , and Siemens NX inside PTC Creo Parametric. Drive Freestyle geometry parametrically With the introduction of a new Align capability inside Freestyle, PTC Creo Parametric users can now create and drive their freeform, stylized designs parametrically. Users have the ability to connect their Freestyle geometry to other external geometry with positional, tangent, or normal conditions. Any changes made to this external geometry will automatically update the Freestyle geometry during regeneration, maintaining the appropriate connection. This allows users to more effectively combine freeform, organic geometry with dimension based design intent. Page 1 of 6 | Top Enhancements in PTC Creo Parametric 3.0 PTC.com Data Sheet Extension New and improved modeling capabilities Chordal/constant width rounds: A new round option has been added in PTC Creo Parametric allowing users to create chordal rounds. -

Vlsi Cad Engineering Grace Gao, Principle Engineer, Rambus Inc
VLSI CAD ENGINEERING GRACE GAO, PRINCIPLE ENGINEER, RAMBUS INC. AUGUST 5, 2017 Agenda • CAD (Computer-Aided Design) ◦ General CAD • CAD innovation over the years (Short Video) ◦ VLSI CAD (EDA) • EDA: Where Electronic Begins (Short Video) • Zoom Into a Microchip (Short Video) • Introduction to Electronic Design Automation ◦ Overview of VLSI Design Cycle ◦ VLSI Manufacturing • Intel: The Making of a Chip with 22nm/3D (Short Video) ◦ EDA Challenges and Future Trend • VLSI CAD Engineering ◦ EDA Vendors and Tools Development ◦ Foundry PDK and IP Reuse ◦ CAD Design Enablement ◦ CAD as Career • Q&A CAD (Computer-Aided Design) General CAD • Computer-aided design (CAD) is the use of computer systems (or workstations) to aid in the creation, modification, analysis, or optimization of a design CAD innovation over the years (Short Video) • https://www.youtube.com/watch?v=ZgQD95NhbXk CAD Tools • Commercial • Freeware and open source Autodesk AutoCAD CAD International RealCAD 123D Autodesk Inventor Bricsys BricsCAD LibreCAD Dassault CATIA Dassault SolidWorks FreeCAD Kubotek KeyCreator Siemens NX BRL-CAD Siemens Solid Edge PTC PTC Creo (formerly known as Pro/ENGINEER) OpenSCAD Trimble SketchUp AgiliCity Modelur NanoCAD TurboCAD IronCAD QCad MEDUSA • ProgeCAD CAD Kernels SpaceClaim PunchCAD Parasolid by Siemens Rhinoceros 3D ACIS by Spatial VariCAD VectorWorks ShapeManager by Autodesk Cobalt Gravotech Type3 Open CASCADE RoutCad RoutCad SketchUp C3D by C3D Labs VLSI CAD (EDA) • Very-large-scale integration (VLSI) is the process of creating an integrated circuit (IC) by combining hundreds of thousands of transistors into a single chip. • The design of VLSI circuits is a major challenge. Consequently, it is impossible to solely rely on manual design approaches. -

F O R D E M a N D I N G C F D Pre- & Post-Processing
for demanding CFD pre- & post-processing DrivAer model, TUM www.beta-cae.com for demanding CFD pre- & post-processing ANSA with its powerful functionality provides high efficiency solutions for CFD applications. Its capabilities meet the industry's demanding needs for external and internal flow simulations, increase productivity, and contribute to the high quality of CFD results. It is the choice of the leaders in CFD simulations in various sectors such as automotive, motorsports and aerospace among others. General features - 64 bit code, for unlimited memory usage - Multi-core CPU usage, taking advantage of all the hardware's CPU power - Double precision for maximum accuracy - Customizable interface with pre-defined CFD oriented layout - CAD interfacing with neutral and native formats such as: IGES, STEP, VDA-FS, Catia v4 and v5, NX, Parasolid, PTC Creo Parametric, SolidWorks, Inventor, JT - Supporting standard and polyhedral meshes - CFD mesh input/output for: ANSYS FLUENT, STAR-CD & CCM+, OpenFOAM, CFD++, DLR-TAU, SC/TETRA, UH-3D, CFX5, CGNS - Pre-processing and interfacing with all major CAE codes (NASTRAN, Abaqus, ANSYS, THESEUS-FE, RadTherm and more) and numerous neutral mesh formats (PATRAN, STL, VRML etc.) - ANSA Scripting, with Python support, allows the automation of tedious pre-processing tasks, such as CAD data input, model structure build up, surface meshing and output, for increased productivity. It also supports the creation of user defined functions, further extending the software's functionality Topology and CAD functionality - Integrated CAD tools for geometry creation, modification, cleanup, defeaturing and watertight preparation - Easy identification and isolation of inner or outer wetted surfaces, internal passages, zero-thickness walls, intersections, proximities and more - Leak detection tools - Automatic identification of similar geometry and substitution with virtual linked geometry in order to speed up model build-up time thanks to the interactive relation between the linked geometries. -

READ THIS FIRST PTC® Creo®
READ THIS FIRST PTC® Creo® 3.0: PTC Creo Parametric, PTC Creo Direct, PTC Creo Layout, PTC Creo Options Modeler, and PTC Creo Simulate Important Installation and Usage Information Directory of Online and DVD-ROM Information Platform Support http://www.ptc.com/partners/hardware/current/support.htm Technical Support https://www.ptc.com/appserver/cs/portal/ PTC Creo Resource Centers PTC Creo Parametric http://www.ptc.com/community/creo3/parametric PTC Creo Layout http://www.ptc.com/community/creo3/layout PTC Creo Options Modeler http://www.ptc.com/community/creo3/options-modeler PTC Creo Simulate http://www.ptc.com/community/creo3/simulate PTC Creo Parametric http://www.ptc.com/community/creo3/direct PTC Creo 30-Day Trial http://www.ptc.com/community/creo3/parametric-30-day-trial Knowledge Base http://www.ptc.com/appserver/cs/search/search.jsp Reference Documents http://www.ptc.com/appserver/cs/doc/refdoc.jsp PTC Creo is a scalable suite of interoperable, right-sized design applications for users across the enterprise to more easily participate in and contribute to the product design process. With these applications, companies can bring better products to market faster by improving processes such as concept design, detailed design, and verification and validation. Installation PTC Creo 3.0 is packaged with a PTC License Server powered by FlexNet Publisher 11.11.1. However, PTC Creo 3.0 can also be used with a PTC License Server powered by FlexNet Publisher 10.8 or later from Flexera Software. If you are already running a license server for Pro/ENGINEER® Wildfire® 3.0 or later, PTC Creo Elements/Pro™ 5.0 or Copyright © 2014 PTC Inc. -

V5i > Creo View User Guide
Visualize 3D for CATIA V5i to CreoView Product Release Version 21.2 USER GUIDE Revision: 1.0 Issued: 08/08/2018 © THEOREM SOLUTIONS 2018 CADverter v21.2 for CATIA V5i - CreoView Contents Overview of Visualize 3D ........................................................................................................... 3 About Theorem ......................................................................................................................3 What is Visualize 3D? .............................................................................................................3 The CATIA V5i Uni-directional CreoView Translator ..............................................................4 Primary Product Features .......................................................................................................4 Primary Product benefits? ......................................................................................................4 CATIA V5I to Creo View PMI Service Module .........................................................................5 CATIA V5I to Creo View JT Add On Module ............................................................................5 CATIA V5I to Creo View 3D PDF Add On Module ...................................................................5 Getting Started .......................................................................................................................... 6 Documentation .......................................................................................................................6 -

ANSA & Μeta : Powerful Pre- and Post-Processing for Advanced CFD
ANSA & μETA : powerful pre- and post-processing for advanced CFD simulations January 2015 BETA CAE Systems S.A. Kato Scholari, Thessaloniki, geometry GR- 57500 Epanomi, Greece Tel :+30-392-021420 Fax :+30-392- 021417 mesh Email : [email protected] URL : http://www.beta-cae.gr morph BETA SystemsS.A. CAE rights BETA All reserved 15 results Copyright Copyright 20 © ANSA and μETA v15.x powerful pre- and post-processing for advanced CFD simulations January 2015 1 ANSA pre-processor specifications Supported platforms: - Linux - Windows XP / Vista / 7 / 8 - MacOS Parallel processing on multi core hardware for maximum speed 64 bit code for unlimited memory usage Double precision for high accuracy By permission of Wirth Research Ltd BETA SystemsS.A. CAE rights BETA All reserved 15 Copyright Copyright 20 © ANSA and μETA v15.x powerful pre- and post-processing for advanced CFD simulations January 2015 2 Input/Output Neutral CAD formats: Native CAD formats: CFD formats: IGES CATIA V4 & V5 Fluent STEP Unigraphics NX Star-CD and CCM+ VDA-FS PTC Creo Parametric (ProE) OpenFOAM JT CFD++ SolidWorks CFX5 Inventor CGNS Parasolid SC/Tetra UH-3D TAU Direct Interfaces with other CAE codes RADTHERM THESEUS-FE NASTRAN Other mesh formats ABAQUS PATRAN BETA SystemsS.A. CAE rights BETA All reserved By permission of Wirth Research Ltd 15 ANSYS STL LS-DYNA VRML Copyright Copyright 20 © and more.. and more.. ANSA and μETA v15.x powerful pre- and post-processing for advanced CFD simulations January 2015 3 Industrial scale pre-processing Powerful generation and visualization of large CFD models High Lift Prediction Workshop II model BETA SystemsS.A.