REBA: a Refinement-Based Architecture for Knowledge Representation and Reasoning in Robotics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Executable Formal Specifications in Game Development
TIMO NUMMENMAA Executable Formal Specifications in Game Development Design, Validation and Evolution ACADEMIC DISSERTATION To be presented, with the permission of the Board of the School of Information Sciences of the University of Tampere, for public discussion in the Auditorium A1 of the Main Building, Kalevantie 4, Tampere, on November 30th, 2013, at 12 o’clock. UNIVERSITY OF TAMPERE ACADEMIC DISSERTATION University of Tampere, School of Information Sciences Finland Copyright ©2013 Tampere University Press and the author Cover design by Mikko Reinikka Acta Universitatis Tamperensis 1875 Acta Electronica Universitatis Tamperensis 1356 ISBN 978-951-44-9275-4 (print) ISBN 978-951-44-9276-1 (pdf) ISSN-L 1455-1616 ISSN 1456-954X ISSN 1455-1616 http://tampub.uta.fi Suomen Yliopistopaino Oy – Juvenes Print Tampere 2013 Abstract Games provide players with enjoyment, escapism, unique experiences and even a way to socialise. Software based games played on electronic devices such as computers and games consoles are a huge business that is still growing. New games are con- tinually developed as demand for these digital games is high. Digital games are often complex and have high requirements for quality. The complexity is especially ap- parent in complex multiplayer games and games that are constantly evolving. This complexity can be problematic in various stages of development. For example, under- standing if a design of a game works as intended can be difficult. Managing changes that need to be made to a game during its lifetime, even after its initial release, is also challenging from both a design and an implementation standpoint. In this thesis these problems are addressed by presenting a method of utilising formal methods for simulations of game designs as a way of development, commu- nication, documentation and design. -

Answer Set Programming
ANSWER SET PROGRAMMING Tran Cao Son Department of Computer Science New Mexico State University Las Cruces, NM 88011, USA [email protected] http://www.cs.nmsu.edu/~tson October 2005 Answer Set Programming. Acknowledgement This tutorial contains some materials from tutorials on answer set programming and on knowledge representation and logic programming from those provided by • Chitta Baral, available at www.public.asu.edu/~cbaral. • Michael Gelfond, available at www.cs.ttu.ued/~mgelfond. Tran Cao Son 1 Answer Set Programming. Introduction — Answer Set Programming Answer set programming is a new programming paradigm. It is introduced in the late 90’s and manages to attracts the intention of different groups of researchers thanks to its: • declarativeness: programs do not specify how answers are computed; • modularity: programs can be developed incrementally; • expressiveness: answer set programming can be used to solve problems in high 2 complexity classes (e.g. ΣP , Π2P , etc.) Answer set programming has been applied in several areas: reasoning about actions and changes, planning, configuration, wire routing, phylogenetic inference, semantic web, information integration, etc. Tran Cao Son 2 Answer Set Programming. Purpose • Introduce answer set programming • Provide you with some initial references, just in case • ...you get excited about answer set programming Tran Cao Son 3 Answer Set Programming. Outline • Foundation of answer set programming: logic programming with answer set semantics (syntax, semantics, early application). • Answer set programming: general ideas and examples • Application of answer set programming in – Knowledge representation – Constraint satisfaction problem – Combinatoric problems – Reasoning about action and change – Planning and diagnostic reasoning • Current issues Tran Cao Son 4 LOGIC PROGRAMMING AND ANSWER SET SEMANTICS Answer Set Programming. -

Action Language for Foundational UML (Alf) Concrete Syntax for a UML Action Language Version 1.1 ______
An OMG® Action Language for Foundational UML™ Publication Action Language for Foundational UML (Alf) Concrete Syntax for a UML Action Language Version 1.1 ____________________________________________________ OMG Document Number: formal/2017-07-04 Date: July 2017 Normative reference: http://www.omg.org/spec/ALF/1.1 Machine readable file(s): Normative: http://www.omg.org/spec/ALF/20170201/Alf-Syntax.xmi http://www.omg.org/spec/ALF/20170201/Alf-Library.xmi http://www.omg.org/spec/ALF/20120827/ActionLanguage-Profile.xmi ____________________________________________________ Copyright © 2010-2013 88solutions Corporation Copyright © 2013 Commissariat à l’Energie Atomique et aux Energies Alternatives (CEA) Copyright © 2010-2017 Data Access Technologies, Inc. (Model Driven Solutions) Copyright © 2010-2013 International Business Machines Copyright © 2010-2013 Mentor Graphics Corporation Copyright © 2010-2013 No Magic, Inc. Copyright © 2010-2013 Visumpoint Copyright © 2010-2017 Object Management Group USE OF SPECIFICATION - TERMS, CONDITIONS & NOTICES The material in this document details an Object Management Group specification in accordance with the terms, conditions and notices set forth below. This document does not represent a commitment to implement any portion of this specification in any company's products. The information contained in this document is subject to change without notice. LICENSES The companies listed above have granted to the Object Management Group, Inc. (OMG) a nonexclusive, royalty- free, paid up, worldwide license to copy and distribute this document and to modify this document and distribute copies of the modified version. Each of the copyright holders listed above has agreed that no person shall be deemed to have infringed the copyright in the included material of any such copyright holder by reason of having used the specification set forth herein or having conformed any computer software to the specification. -

Planning in Action Language BC While Learning Action Costs for Mobile Robots
Planning in Action Language BC while Learning Action Costs for Mobile Robots Piyush Khandelwal, Fangkai Yang, Matteo Leonetti, Vladimir Lifschitz and Peter Stone Department of Computer Science The University of Texas at Austin 2317 Speedway, Stop D9500 Austin, TX 78712, USA fpiyushk,fkyang,matteo,vl,[email protected] Abstract 1999). Furthermore, the action language BC (Lee, Lifschitz, and Yang 2013) can easily formalize recursively defined flu- The action language BC provides an elegant way of for- ents, which can be useful in robot task planning. malizing dynamic domains which involve indirect ef- fects of actions and recursively defined fluents. In com- The main contribution of this paper is a demonstration plex robot task planning domains, it may be necessary that the action language BC can be used for robot task for robots to plan with incomplete information, and rea- planning in realistic domains, that require planning in the son about indirect or recursive action effects. In this presence of missing information and indirect action effects. paper, we demonstrate how BC can be used for robot These features are necessary to completely describe many task planning to solve these issues. Additionally, action complex tasks. For instance, in a task where a robot has to costs are incorporated with planning to produce opti- collect mail intended for delivery from all building residents, mal plans, and we estimate these costs from experience the robot may need to visit a person whose location it does making planning adaptive. This paper presents the first not know. To overcome this problem, it can plan to complete application of BC on a real robot in a realistic domain, its task by asking someone else for that person’s location, which involves human-robot interaction for knowledge acquisition, optimal plan generation to minimize navi- thereby acquiring this missing information. -

PDF Hosted at the Radboud Repository of the Radboud University Nijmegen
PDF hosted at the Radboud Repository of the Radboud University Nijmegen The following full text is a publisher's version. For additional information about this publication click this link. http://hdl.handle.net/2066/181589 Please be advised that this information was generated on 2021-10-05 and may be subject to change. A Cocktail of Tools Domain-Specific Languages for Task-Oriented Software Development Jurriën Stutterheim ACocktailofTools Domain-Specific Languages for Task-Oriented Software Development Proefschrift ter verkrijging van de graad van doctor aan de Radboud Universiteit Nijmegen op gezag van de rector magnificus prof. dr. J.H.J.M. van Krieken, volgens besluit van het college van decanen in het openbaar te verdedigen op vrijdag 17 november 2017 om 10:30 uur precies door Jurri¨en Stutterheim geboren op 2 december 1985 te Middelburg Promotor: Prof. dr. ir. M.J. Plasmeijer Copromotoren: Dr. P.M. Achten Dr. J.M. Jansen (Nederlandse Defensie Academie, Den Helder) Manuscriptcommissie: Prof. dr. R.T.W. Hinze Prof. dr. S.D. Swierstra (Universiteit Utrecht) Prof. dr. S.B. Scholz (Heriot-Watt University, Edinburgh, Schotland) Dit onderzoek, met uitzondering van hoofdstuk 2, is ge- financieerd door de Nederlandse Defensie Academie en TNO via het TNO Defensie Onderzoek AIO programma. ISBN: 978-94-92380-74-6 CONTENTS Contents 1 Introduction 1 1.1 Embedded Domain-Specific Languages . 3 1.2 Task-Oriented Programming with iTasks . 4 1.3 Blueprints................................ 4 1.3.1 StaticBlueprints ........................ 5 1.3.2 DynamicBlueprints . 6 1.3.3 GeneralisingBlueprints . 7 1.4 ThesisOutline ............................. 8 2 Building JavaScript Applications with Haskell 11 2.1 Introduction.............................. -

Action Language BC: Preliminary Report
Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence Action Language BC: Preliminary Report Joohyung Lee1, Vladimir Lifschitz2 and Fangkai Yang2 1School of Computing, Informatics and Decision Systems Engineering, Arizona State University [email protected] 2 Department of Computer Science, Univeristy of Texas at Austin fvl,[email protected] Abstract solves the frame problem by incorporating the commonsense law of inertia in its semantics, which makes it difficult to talk The action description languages B and C have sig- about fluents whose behavior is described by defaults other nificant common core. Nevertheless, some expres- than inertia. The position of a moving pendulum, for in- sive possibilities of B are difficult or impossible to stance, is a non-inertial fluent: it changes by itself, and an simulate in C, and the other way around. The main action is required to prevent the pendulum from moving. The advantage of B is that it allows the user to give amount of liquid in a leaking container changes by itself, and Prolog-style recursive definitions, which is impor- an action is required to prevent it from decreasing. A spring- tant in applications. On the other hand, B solves loaded door closes by itself, and an action is required to keep the frame problem by incorporating the common- it open. Work on the action language C and its extension C+ sense law of inertia in its semantics, which makes was partly motivated by examples of this kind. In these lan- it difficult to talk about fluents whose behavior is guages, the inertia assumption is expressed by axioms that the described by defaults other than inertia. -

Kronos Meta-Sequencer – from Ugens to Orchestra, Score and Beyond
Kronos Meta-Sequencer – From Ugens to Orchestra, Score and Beyond Vesa Norilo Centre for Music & Technology University of Arts Helsinki [email protected] ABSTRACT 2. BACKGROUND This article discusses the Meta-Sequencer, a circular com- bination of an interpreter, scheduler and a JIT compiler for Contemporary musical programming languages often blur musical programming. Kronos is a signal processing lan- the lines between ugen, orchestra and score. Semantically, guage focused on high computational performance, and languages like Max [5] and Pure Data [6] would seem to the addition of the Meta-Sequencer extends its reach up- provide just the Orchestra layer; however, they typically wards from unit generators to orchestras and score-level come with specialized unit generators that enable score- programming. This enables novel aspects of temporal re- like functionality. Recently, Max has added a sublanguage cursion – a tight coupling of high level score abstractions called Gen to address ugen programming. with the signal processors that constitute the fundamental SuperCollider [7] employs an object-oriented approach building blocks of musical programs. of the SmallTalk tradition to musical programming. It pro- vides a unified idiom for describing orchestras and scores 1. INTRODUCTION via explicit imperative programs. ChucK [8] introduces timing as a first class language con- Programming computer systems for music is a diverse prac- struct. ChucK programs consist of Unit Generator graphs tice; it encompasses everything from fundamental synthe- with an imperative control script that can perform interven- sis and signal processing algorithms to representing scores tions at precisely determined moments in time. To draw an and generative music; from carefully premeditated pro- analogy to MUSIC-N, the control script is like a score – grams for tape music to performative live coding. -

REFINING the SEMANTICS for EPISTEMIC LOGIC PROGRAMS by Patrick Thor Kahl, M.S. a Dissertation in COMPUTER SCIENCE Submitted to T
REFINING THE SEMANTICS FOR EPISTEMIC LOGIC PROGRAMS by Patrick Thor Kahl, M.S. A Dissertation in COMPUTER SCIENCE Submitted to the Graduate Faculty of Texas Tech University in Partial Fulfillment of the Requirements for the Degree of DOCTOR OF PHILOSOPHY Approved Richard Watson Chair of Committee Michael Gelfond Yuanlin Zhang Mark Sheridan Dean of the Graduate School May 2014 Copyright © 2014 by Patrick Thor Kahl To my family \Exploit symmetry whenever possible. Do not destroy it lightly." |Edsger Dijkstra (1930-2002) Texas Tech University, Patrick Thor Kahl, May 2014 ACKNOWLEDGMENTS My sincere thanks to the members of my committee who were all instrumental in the success of my research goal. My advisor, Dr. Richard Watson, who kindly agreed to take me in as his doctoral student, was a pleasure to work with on this topic. I appreciate all the hours he spent guiding me, sharing the ups and downs of one after another failure, yet maintaining the fervent belief that we were ever closer to our goal. In short, he was able to make this task an exciting endeavor, sharing with me in the adventure of scientific research. It was Dr. Michael Gelfond who introduced Epistemic Specifications to the world in the early 1990s, and he has continued to lead in its development, particularly in recent years with the increase in interest. His keen insight concerning the various different modal reducts proposed and whether they reflected how a rational agent should pick from among different models kept me from abandoning what eventually became the definition presented herein. The new definition led to a new intuition concerning the world views of various programs, one that I now believe is correct and also beautiful. -
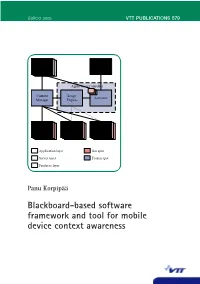
Blackboard-Based Software Framework and Tool for Mobile Device Context Awareness Panu Korpipää Panu
ESPOO 2005 VTT PUBLICATIONS 579 VTT PUBLICATIONS 579 Mobile context awareness research aims at providing the mobile device user with a way of usage that suits the situation. New input sources, such as Application / embedded sensors producing interaction-related information, are becoming ContextContext Customizer Actionsources available for mobile devices. These input sources enable novel ways of sources interacting with the devices, and even open possibilities to create entirely new types of applications. To facilitate the full potential of utilising such Blackboard-based new input sources, a software framework is required with a uniform means Application Controller of acquiring and processing interaction-related information, and providing Context Script Activator it for the applications. The main result of this dissertation was a software Manager Engine framework and tool for facilitating the rapid development of mobile device context-aware applications. The framework provides a publish and sub- scribe mechanism, database, and a customisable application controller. For software developers the framework provides an application programming interface. The customization tool enables end-user development of interaction-related Context Context Change ContextContext ContextContext ContextContext features in mobile devices. The results have commercial value; they are framework Source Abstractor Detector sourcessources sourcessources sourcessources utilised by the telecommunication industry for application domains such as enhanced usability and -

On Language Interfaces Thomas Degueule, Benoit Combemale, Jean-Marc Jézéquel
On Language Interfaces Thomas Degueule, Benoit Combemale, Jean-Marc Jézéquel To cite this version: Thomas Degueule, Benoit Combemale, Jean-Marc Jézéquel. On Language Interfaces. Bertrand Meyer; Manuel Mazzara. PAUSE: Present And Ulterior Software Engineering, Springer, 2017. hal-01424909 HAL Id: hal-01424909 https://hal.inria.fr/hal-01424909 Submitted on 3 Jan 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. On Language Interfaces Thomas Degueule, Benoit Combemale, and Jean-Marc Jézéquel Abstract Complex systems are developed by teams of experts from multiple do- mains, who can be liberated from becoming programming experts through domain- specific languages (DSLs). The implementation of the different concerns of DSLs (including syntaxes and semantics) is now well-established and supported by various languages workbenches. However, the various services associated to a DSL (e.g., editors, model checker, debugger or composition operators) are still directly based on its implementation. Moreover, while most of the services crosscut the different DSL concerns, they only require specific information on each. Consequently, this prevents the reuse of services among related DSLs, and increases the complexity of service implementation. Leveraging the time-honored concept of interface in software engineering, we discuss the benefits of language interfaces in the context of software language engineering. -

Application of Model-Driven Engineering and Metaprogramming to DEVS Modeling & Simulation
Application of Model-Driven Engineering and Metaprogramming to DEVS Modeling & Simulation Luc Touraille To cite this version: Luc Touraille. Application of Model-Driven Engineering and Metaprogramming to DEVS Model- ing & Simulation. Other. Université Blaise Pascal - Clermont-Ferrand II, 2012. English. NNT : 2012CLF22308. tel-00914327 HAL Id: tel-00914327 https://tel.archives-ouvertes.fr/tel-00914327 Submitted on 5 Dec 2013 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. D.U.: 2308 E.D.S.P.I.C: 594 Ph.D. Thesis submitted to the École Doctorale des Sciences pour l’Ingénieur to obtain the title of Ph.D. in Computer Science Submitted by Luc Touraille Application of Model-Driven Engineering and Metaprogramming to DEVS Modeling & Simulation Thesis supervisors: Prof. David R.C. Hill Dr. Mamadou K. Traoré Publicly defended on December 7th, 2012 in front of an examination committee composed of: Reviewers: Prof. Jean-Pierre Müller, Cirad, Montpellier Prof. Gabriel A. Wainer, Carleton University, Ottawa Supervisors: Prof. David R.C. Hill, Université Blaise Pascal, Clermont-Ferrand Dr. Mamadou K. Traoré, Université Blaise Pascal, Clermont- Ferrand Examiners Dr. Alexandre Muzy, Università di Corsica Pasquale Paoli, Corte Prof. -

Software Engineering Answer Set Programming
Software Engineering for Answer Set Programming Second International Workshop 14 September 2009, Potsdam, Germany Marina De Vos Torsten Schaub (Eds.) Preface Over the last ten years, answer set programming (ASP) has grown from a pure theo- retical knowledge representation and reasoning formalism to a computational approach with a very strong formal backing. At present, ASP is seen as the computational em- bodiment of non-monotonic reasoning incorporating techniques of databases, knowl- edge representation, logic and constraint programming. ASP has become an appeal- ing tool for knowledge representation and reasoning and thanks to the increasing effi- ciency of the implementations of ASP solvers, the field has now started to tackle many industrially-relevant applications. Writing complex programs in any language is not an easy task, with ASP being no exception. Most of the modern popular programming languages have an abundance of tools and development methodologies to facilitate and improve the coding process. Given the differences in for example language design, execution, and application do- mains for languages such as Java and C++, the existing methodologies and tools that are available are mostly not suitable for ASP. Therefore development tools and software engineering methodologies specifically designed for ASP are required. The SEA’09 workshop provides an international forum to discuss all software engi- neering issues the field currently faces or in the future will experience. SEA’09 is the second first event in hopefully a long series of workshops. The first workshop was held in Tempe, Arizona, USA as a co-located workshop of LPNMR’07, one of the leading conferences in the area of logic programming and in particular ASP.