Variationally Consistent Isogeometric Analysis of Trimmed Thin Shells at finite Deformations, Based on the STEP Exchange Format
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

ISIGHT Brochure
ISIGHT AUTOMATE DESIGN EXPLORATION AND OPTIMIZATION ISIGHT INDUSTRY CHALLENGES In today’s computer-aided product development and manufacturing environment, designers and engineers are using a wide range of KEY BENEFITS software tools to design and simulate their products. Often, the • Reduce time and costs parameters and results from one software package are required as • Improve product reliability inputs to another package, and the manual process of entering the required data can reduce efficiency, slow product development, and • Gain competitive advantage introduce errors in modeling and simulation assumptions. SIMULIA’s Isight Solution Isight provides designers, engineers, and researchers with an open system for integrating design and simulation models—created with various CAD, CAE, and other software applications—to automate the execution of hundreds or thousands of simulations. Isight allows users to save time and improve their products by optimizing them against performance or cost metrics through statistical methods, such as Design of Experiments (DOE) or Design for Six Sigma. Isight combines cross-disciplinary models and applications together in a simulation process flow, automates their execution, explores the resulting design space, and identifies the optimal design Isight parameters based on required constraints. Isight’s ability to manipulate and map parametric data between process steps and automate multiple simulations greatly improves efficiency, reduces manual errors, and accelerates the evaluation of product design alternatives. Open Component Framework Isight provides a standard library of components— including Excel™, Word™, CATIA V5™, Dymola™, MATLAB®, COM, Text I/O applications, Java and Python Scripting, and databases—for integrating and running a model or simulation. These components form the building blocks of simulation process flows. -

Dassault Systèmes Annual Report 2018 1 General
NOUSWE 2018 SOMMESARE Financial report THERELÀ CONTENTS General 2 Person Responsible 3 15Presentation of the Group 5 Corporate governance 167 1.1 Profile of Dassault Systèmes 6 5.1 The Board’s Corporate Governance Report 168 1.2 Financial Summary: A Long History 5.2 Internal Control Procedures and Risk Management 203 of Sustainable Growth 7 5.3 Transactions in Dassault Systèmes shares 1.3 History 9 by the Management of the Company 207 1.4 Group Organization 14 5.4 Statutory Auditors 210 1.5 Business Activities 15 5.5 Declarations regarding the administrative Bodies 1.6 Research and development 29 and Senior Management 210 1.7 Risk factors 31 Information about Social, societal and environmental 6 Dassault Systèmes SE, the share capital 2 responsibility 39 and the ownership structure 211 6.1 Information about Dassault Systèmes SE 212 2.1 Social responsibility 41 6.2 Information about the Share Capital 216 2.2 Societal responsibility 48 6.3 Information about the Shareholders 219 2.3 Environmental Responsibility 53 6.4 Stock Market Information 224 2.4 Business Ethics and Vigilance Plan 58 2.5 Reporting methodology 61 2.6 Independent Verifier’s Report on Consolidated Non- General Meeting 225 financial Statement Presented in the Management 7 Report 64 7.1 Presentation of the resolutions proposed by the 2.7 Statutory Auditors’ Attestation on the information Board of Directors to the General Meeting on relating to the Dassault Systèmes SE’s total amount May 23, 2019 226 paid for sponsorship 67 7.2 Text of the draft resolutions proposed by the -

Simulia Community News
SIMULIA COMMUNITY NEWS #08 October 2014 THE POWER OF THE PORTFOLIO COVER STORY SIMULATION HELPS UPGRADE LONDON TUNNELS in this Issue October 2014 3 Welcome Letter Scott Berkey, Chief Executive Officer, SIMULIA 4 Portfolio Update Latest SIMULIA Portfolio Releases Deliver Powerful, Advanced Simulation Functionality to Users 8 Strategy Overview DR. SAUER How to Stay at the Top of Your Game in the Fast-Evolving 10 World of Simulation 10 Cover Story Dr. Sauer and Partners Helps Upgrade London Underground Station 13 News SIMPACK Joins the Dassault Systèmes Family 14 Case Study Stadler Rail Simulates Train Safety with FEA 17 Alliances Topology and Shape Optimization Using the Tosca-Ansa Environment 18 Case Study Fine-tuning the Anatomy of Car-Seat Comfort STADLER 20 Academic Update 14 Oil & Gas Subsurface Innovation with Multiphysics Simulations 22 Tips & Tricks Optimization Module Within Abaqus/CAE Contributors: Dr. Alois Starlinger (Stadler Rail), Dr. Alexander Siefert (Wölfel Group), Jeremy Brown and Randi Jean Walters (Stanford University), Parker Group On the Cover: Ali Nasekhian, Dr. techn., M.Sc. Senior Tunnel Engineer, Dr. Sauer and Partners Cover photo by Roger Brown Photography WÖLFEL 18 SIMULIA Community News is published by Dassault Systèmes Simulia Corp., Rising Sun Mills, 166 Valley Street, Providence, RI 02909-2499, Tel. +1 401 276 4400, Fax. +1 401 276 4408, [email protected], www.3ds.com/simulia Editor: Tad Clarke Associate Editor: Kristina Hines Graphic Designer: Todd Sabelli ©2014 Dassault Systèmes. All rights reserved. 3DEXPERIENCE, the Compass icon and the 3DS logo, CATIA, SOLIDWORKS, ENOVIA, DELMIA, SIMULIA, GEOVIA, EXALEAD, 3D VIA, BIOVIA, NETVIBES, and 3DXCITE are commercial trademarks or registered trademarks of Dassault Systèmes or its subsidiaries in the U.S. -
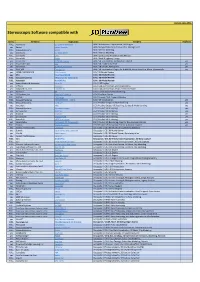
Stereo Software List
Version: June 2021 Stereoscopic Software compatible with Stereo Company Application Category Duplicate FULL Xeometric ELITECAD Architecture BIM / Architecture, Construction, CAD Engine yes Bexcel Bexcel Manager BIM / Design, Data, Project & Facilities Management FULL Dassault Systems 3DVIA BIM / Interior Modeling yes Xeometric ELITECAD Styler BIM / Interior Modeling FULL SierraSoft Land BIM / Land Survey Restitution and Analysis FULL SierraSoft Roads BIM / Road & Highway Design yes Xeometric ELITECAD Lumion BIM / VR Visualization, Architecture Models yes yes Fraunhofer IAO Vrfx BIM / VR enabled, for Revit yes yes Xeometric ELITECAD ViewerPRO BIM / VR Viewer, Free Option yes yes ENSCAPE Enscape 2.8 BIM / VR Visualization Plug-In for ArchiCAD, Revit, SketchUp, Rhino, Vectorworks yes yes OPEN CASCADE CAD CAD Assistant CAx / 3D Model Review yes PTC Creo View MCAD CAx / 3D Model Review FULL Dassault Systems eDrawings for Solidworks CAx / 3D Model Review FULL Autodesk NavisWorks CAx / 3D Model Review yes Robert McNeel & Associates. Rhino (5) CAx / CAD Engine yes Softvise Cadmium CAx / CAD, Architecture, BIM Visualization yes Gstarsoft Co., Ltd HaoChen 3D CAx / CAD, Architecture, HVAC, Electric & Power yes Siemens NX CAx / Construction & Manufacturing Yes 3D Systems, Inc. Geomagic Freeform CAx / Freeform Design FULL AVEVA E3D Design CAx / Process Plant, Power & Marine FULL Dassault Systems 3DEXPERIENCE - CATIA CAx / VR Visualization yes FULL Dassault Systems ICEM Surf CGI / Product Design, Surface Modeling yes yes Autodesk Alias CGI / Product -

Developing Downhole Oil and Gas Drilling Products Faster with Simuliaworks
DEVELOPING DOWNHOLE OIL AND GAS DRILLING PRODUCTS FASTER WITH SIMULIAWORKS By adding SIMULIAworks to its SOLIDWORKS product development implementation, InFocus Energy Services has acquired the simulation power and efficiency that it needs to consistently develop innovative, effective downhole products for the oil and gas industry more quickly and affordably. Challenge: launching a new 3DEXPERIENCE® simulation solution that Leverage high-end, nonlinear structural incorporated the SIMULIA® Abaqus solver, we signed up for simulation technology to reduce reliance on the Lighthouse Program so we could start using the new costly, time-consuming physical testing and SIMULIAworks immediately. As soon as we got our hands on develop innovative downhole drilling products it, we started testing it and benchmarking it against known test results.” more quickly and cost-effectively. SIMULATING TRICKY, COMPLEX CONTACT ACCURATELY Solution: Add SIMULIAworks to its SOLIDWORKS InFocus first utilized SIMULIAworks on the bearing section implementation to conduct nonlinear structural of the company’s RE|FLEX Premium HP/HT Drilling Motor. The motor’s bearing section is a proprietary design that was and complex contact analyses in the cloud developed to convert extreme loading parameters, including to advance and accelerate new product torque of over 30,000 foot-pounds, into efficient drilling action. development. The company’s initial concept design of the drive system, which utilized traditional ball bearings, resulted in failure during Results: testing when the load crushed the bearings and the faces that • Saved tens of thousands of dollars in testing costs load the bearings. SIMULIAworks predicted the failure—with • Cut months of time and extra labor from accurate correlation to actual test results—and helped the development process company develop a better, more innovative design. -

Simulation Lifecycle Management Manage & Secure Simulation Intellectual Property 3DS.COM/SIMULIA SIMULIA SLM
Simulation Lifecycle Management Manage & Secure Simulation Intellectual Property 3DS.COM/SIMULIA SIMULIA SLM Industry Challenges In the manufacturing industry, design analysis technology and related methods are being used to create innovative and reliable products while reducing time and costs. However, even those companies gaining significant benefits from simulation will admit that they often fail to capture their simulation processes or Capture best practices manage the results in a manner that allows effective knowledge reuse or decision-making traceability. Reuse intellectual property SIMULIA Solutions Improve process quality SIMULIA Simulation Lifecycle Management (SLM) solutions simplify the capture and deployment of approved simulation methods and best practices, providing guidance and improved confidence in the use of simulation results for collaborative decision making. Users can improve product quality with fully traceable simulation history and associated data. SLM also accelerates product development by providing timely access to the right information through secure storage, search and retrieval with distinct functionality dedicated specifically to simulation scenarios and data. rt po up P S ro n c io e s s i s c e M D a n a g e m Collaboration e n t D a ta M an agement Improve your simulation data and process quality The SIMULIA SLM solution portfolio, includes Scenario Definition, Live Simulation Review, Isight, and the SIMULIA Execution Engine. Scenario Definition enables methods developers to create workflow-specific simulation templates incorporating their company’s best practices while using the simulation tools of their choosing. These templates can then be deployed to a wide range of users ensuring adherence to standard practices in order to improve repeatability, reliability and confidence in simulations. -

2020 Universal Registration Document
2020 2018/2019/2020 Universal Registration Document CONTENTS General 2 Person Responsible 3 1 Presentation of the Company 5 4 Financial statements 105 2020 Performance and Strategy 6 4.1 Consolidated Financial Statements 106 1.1 Key data 8 4.2 Parent company financial statements 153 1.2 Profile of Dassault Systèmes & Our Purpose 10 4.3 Legal and Arbitration Proceedings 184 1.3 History and Development of the Company 13 1.4 Business Activities 18 Corporate governance 185 1.5 Research and development 31 5 1.6 Company Organization 34 5.1 The Board’s Corporate Governance Report 186 1.7 Financial Summary: five-year historical information 36 5.2 Internal Control Procedures and Risk Management 229 1.8 Extra-financial performance 38 5.3 Transactions in Dassault Systèmes shares by the 1.9 Risk Factors 39 Management of Dassault Systèmes 233 5.4 Information on the Statutory Auditors 237 5.5 Declarations regarding the administrative Social, societal and environmental and management bodies 237 2 responsibility 47 2.1 Sustainability Governance 49 Information about 2.2 Social, societal and environmental risks 49 6 Dassault Systèmes SE, the share capital 2.3 Social responsibility 50 and the ownership structure 239 2.4 Societal responsibility 56 6.1 Information about Dassault Systèmes SE 240 2.5 Environmental responsibility 61 6.2 Information about the Share Capital 244 2.6 Business Ethics and Vigilance Plan 67 6.3 Information about the Shareholders 247 2.7 Environmental, Social and Governance metrics 74 6.4 Stock Market Information 253 2.8 Reporting Methodology -

Dassault Systèmes Announces the Release of SIMULIA SLM for Simulation Lifecycle Management
Dassault Systèmes Announces the Release of SIMULIA SLM for Simulation Lifecycle Management New Software Secures Valuable Intellectual Property Through Management of Simulation Data, Processes, and Applications Paris, France, and Providence, R.I., USA, January 16, 2008 – Dassault Systèmes (DS) (Nasdaq: DASTY; Euronext Paris: #13065, DSY.PA), a world leader in 3D and Product Lifecycle Management (PLM) solutions, today announced the early availability of SIMULIA SLM, a new product suite from its SIMULIA brand that will have a positive impact on the way that organizations perform and manage their simulation processes. The use of simulation has become an increasingly vital process in developing innovative products quickly. SIMULIA SLM accelerates the product development lifecycle by providing timely access to the right information through secure storage, search, and retrieval functionality that is specific to simulation processes and data. SIMULIA SLM maximizes the value of company-generated intellectual property (IP) through the capture, re-use, and deployment of simulation best practices. It also provides tools for control and sharing of simulation data for collaborative product development. “The release of SIMULIA SLM marks a major milestone for SIMULIA as we expand our product portfolio beyond the Abaqus product line,” said Mark Goldstein, CEO, SIMULIA. “By leveraging PLM technology from ENOVIA and simulation expertise from SIMULIA, we have been able to rapidly develop what we believe is an industry-leading solution. SIMULIA SLM will enable our customers to secure their simulation intellectual property and transform it into a valuable and controlled corporate asset.” Shorter product lifecycles, higher costs, stricter regulations, and the desire to benefit from a greater number of simulations make it clear that companies need an economical and effective solution to manage, share, and secure their simulation assets. -

Abaqus for CATIA V5
Abaqus for CATIA V5 R21 CATIA V5 Integration • Temperature-dependent material properties • Thermal properties Integration Features • Linear elasticity • Availability of linear and nonlinear static, dynamic, and thermal • Metal plasticity (isotropic, kinematic, or analysis capabilities within the CATIA V5 environment Johnson-Cook hardening) • Complete geometric associativity • Hyperelasticity • Support for Knowledgeware, publications, and results sensors • Abaqus material user subroutine • Model optimization using the PEO workbench • Abaqus heat generation user subroutine • Support for analysis assembly • Composite properties imported from the CATIA Composite • Complete support for CATIA V5 groups Design workbench • Support for many CATIA V5 advanced connections • Orthotropic composite layups for shell modeling • Visual Basic scripting capabilities for automated workflows • 3-D orthotropic material properties • Gasket material properties Operating Systems • Windows/x86-32 and Windows/x86-64 operating systems Loads (Windows XP Professional SP2, Windows XP Professional x64, • Load application using tabular and smooth-step amplitudes Windows Vista, Windows 7) • Forces and moments can follow nodal rotation • Data mapping available for pressure, heat flux, thermal Abaqus Workbenches film condition, and temperature • Nonlinear Structural Analysis workbench for static, • Imported loads from GPS analysis frequency-extraction, and explicit dynamic simulations • Cartesian, cylindrical, and spherical local coordinate • Thermal Analysis workbench for -

Developing Downhole Oil and Gas Drilling Products Faster with Simulia Structural Simulation Engineer
DEVELOPING DOWNHOLE OIL AND GAS DRILLING PRODUCTS FASTER WITH SIMULIA STRUCTURAL SIMULATION ENGINEER By adding SIMULIA SSE analysis software to its SOLIDWORKS product development implementation, InFocus Energy Services has acquired the simulation power and efficiency that it needs to consistently develop innovative, effective downhole products for the oil and gas industry more quickly and affordably. Challenge: 3DEXPERIENCE® simulation solution that incorporated the Leverage high-end, nonlinear structural SIMULIA® Abaqus solver, we signed up for the Lighthouse simulation technology to reduce reliance on Program so we could start using the new SIMULIA Structural costly, time-consuming physical testing and Simulation Engineer immediately. As soon as we got our hands develop innovative downhole drilling products on it, we started testing it and benchmarking it against known test results.” more quickly and cost-effectively. SIMULATING TRICKY, COMPLEX CONTACT ACCURATELY Solution: InFocus first utilized SIMULIA Structural Simulation Engineer Add SIMULIA Structural Simulation Engineer on the bearing section of the company’s RE|FLEX Premium to its SOLIDWORKS implementation to conduct HP/HT Drilling Motor. The motor’s bearing section is a nonlinear structural and complex contact proprietary design that was developed to convert extreme analyses in the cloud to advance and accelerate loading parameters, including torque of over 30,000 foot- new product development. pounds, into efficient drilling action. The company’s initial concept design of the drive system, which utilized traditional Results: ball bearings, resulted in failure during testing when the load • Saved tens of thousands of dollars in testing costs crushed the bearings and the faces that load the bearings. • Cut months of time and extra labor from SIMULIA Structural Simulation Engineer predicted the failure— development process with accurate correlation to actual test results—and helped the • Realized close correlation between simulation and company develop a better, more innovative design. -

Top Ten Reasons to Embrace Spatial Components in 3D Application Design Introduction
Top Ten Reasons to Embrace Spatial Components in 3D Application Design Introduction Successfully developing, deploying, and supporting 3D applications is a substantial challenge, requiring significant investment, precise execution, and focus on innovation and differentiation. 3D application development faces a variety of hurdles: hitting time-to-market goals, coming in under budget, producing a high quality product, and providing the functionality your customers require. Any one of these challenges can derail an otherwise smooth application deployment. To mitigate risk, software developers require a recognized partner that provides knowledge, experience, proven technology, and predictable deliverables. For nearly thirty years, Spatial Corp., a Dassault Systèmes subsidiary, has developed strong partnerships with market-leading software developers, providing software components for design applications across a broad range of industries. By leveraging Spatial’s 3D software development kits (SDKs) in their application development, Spatial customers can overcome common challenges— allowing them to focus on their unique core competencies, increase product innovation, and build competitive differentiation. Top 10 Reasons to Embrace Spatial Components Explore the rest of this eBook to discover the top 10 reasons to embrace Spatial’s 1 Modeling . 4 6 Predictability . 14 2 Visualization . 6 7 Breadth of Solutions . 16 3D SDK for improving 3D application development—resulting in higher-quality 3 Interoperability . 8 8 Collaboration . 18 deployments, delivered on time and under budget. 4 Future-proof . 10 9 Time-to-revenue . 20 5 Quality . 12 10 Experienced Business Partner . 22 2 Top 10 Reasons to Embrace Spatial Components Top 10 Reasons to Embrace Spatial Components 3 Modeling This video illustrates 1 feature recognition Spatial is the premier supplier of components used in 3D modeling application in Spatial’s ACIS 3D development. -

Optimization of Tow-Steered Composite Wind Turbine Blades for Static Aeroelastic Performance Stephen Michael Barr Lehigh University
Lehigh University Lehigh Preserve Theses and Dissertations 2018 Optimization of Tow-Steered Composite Wind Turbine Blades for Static Aeroelastic Performance Stephen Michael Barr Lehigh University Follow this and additional works at: https://preserve.lehigh.edu/etd Part of the Mechanical Engineering Commons Recommended Citation Barr, Stephen Michael, "Optimization of Tow-Steered Composite Wind Turbine Blades for Static Aeroelastic Performance" (2018). Theses and Dissertations. 4222. https://preserve.lehigh.edu/etd/4222 This Thesis is brought to you for free and open access by Lehigh Preserve. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of Lehigh Preserve. For more information, please contact [email protected]. Optimization of Tow-Steered Composite Wind Turbine Blades for Static Aeroelastic Performance by Stephen M. Barr A Thesis Presented to the Graduate and Research Committee of Lehigh University in Candidacy for the Degree of Master of Science in Mechanical Engineering and Mechanics Lehigh University May 2018 c Copyright by Stephen M. Barr 2018 All Rights Reserved ii This thesis is accepted and approved in partial fulfilment of the requirements for the degree of Master of Science in Mechanical Engineering. Date Dr. Justin W. Jaworski, Thesis Advisor Prof. D. Gary Harlow, Chairperson of Department of Mechanical Engineering and Mechanics iii Acknowledgements I would like to thank my advisor, Dr. Justin W. Jaworski, for the guidance and patience he provided to me throughout this research. I am grateful to not only have had his mentorship in this work, but also in future endeavors. I would also like to thank my employer, Combustion Research and Flow Technology, Inc., and my colleagues who have always been so generous to share their extensive knowledge and experience with me throughout my career and education at Lehigh.