DOCSLIB.ORG

Modulation Classification in Fading Channels Using Antenna Arrays

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modulation Classification in Fading Channels Using Antenna Arrays MODULATION CLASSIFICATION IN FADING CHANNELS USING ANTENNA ARRAYS Ali Abdi1, Octavia A. Dobre1, Rahul Choudhry1, Yeheskel Bar-Ness1, and Wei Su2 1CCSPR, Dept. of ECE, New Jersey Institute of Technology, Newark, NJ 07102, USA 2 CECOM, Fort Monmouth, NJ 07703, USA ABSTRACT ϕ0 is the channel phase (which also includes the carrier ()i N phase offset), {}skk=1 represents the N complex Blind modulation classification (MC) is an intermediate transmitted data symbols, taken from the i-th finite- step between signal detection and demodulation, and plays a alphabet modulation format, and † is the transpose key role in various civilian and military applications In this operator. Depending on the classification approach, in paper, first we provide an overview of decision-theoretic Section IV we consider α0 and ϕ0 as random variables, MC approaches. Then we derive the average likelihood ratio denoted by α and ϕ , respectively, and average over (ALR) based classifier for linear and nonlinear them, whereas in Section V, α and ϕ are considered as modulations, in noisy channels with unknown carrier phase 0 0 unknown deterministic quantities, for which αˆ0 and ϕˆ0 offset and also in Rayleigh fading channels. Since these are provided as their estimates. In any case, we treat the ALR-based classifiers are complex to implement, we then ()i N data symbols {}skk=1 as independent and identically develop a quasi hybrid likelihood ratio (QHLR) based distributed (iid) randoms, and average over them. With classifier, where the unknown parameters are estimated symbol period T0 , rectangular unit-amplitude pulse shape using low-complexity techniques. This QHLR-based ut() of length T , and j 2 =−1 , st(;u ) is given by T0 0 i,0 classifier is much simpler to implement and is also N jϕ0 ()i applicable to any fading distribution, including Rayleigh and st(;uikT,0 )=−−≤≤α 0 e s () tu ( t ( k 1) T 0 ),0 t NT 0 . (1) Rice. Afterwards, we propose a generic multi-antenna ∑k =1 0 classifier for linear and nonlinear modulations, using an Eq. (1) is applicable to M-ary ASK, PSK, QAM, and antenna array at the receiver. This classifier has the FSK modulations. In MASK we have potential to improve the performance of traditional single- sM(MASK) ∈ {±± 1, 3,..., ± ( − 1)} , where M is even. The antenna classifiers, including the proposed QHLR-based symbols of MPSK are given by se(MPSK) = jθm , in which algorithm, via spatial diversity. Simulation results are θm = 2π mM , m=− 0, 1, ..., M 1 , with M as a power of provided to show the performance enhancement offered by two. For square and cross QAM symbols, see [1]. In the new QHLR-based multi-antenna classifier, in a variety MFSK, the symbols are given by ste(MFSK)()= jft 2π m , such of channel and fading conditions. that fmd= ±±ff00, 3 d , ..., ± ( Mf − 1) d 0, with fd 0 as the frequency spacing between any two adjacent constellation I. INTRODUCTION points and M as a power of two. As mentioned in the Modulation identification of a received signal is of footnote of this page, for linear modulations, the data importance in a variety of military and commercial symbols do not depend on t. This property simplifies the applications. Some examples include spectrum monitoring general classifier derived in Section IV. and management, surveillance and control of broadcasting Let us define the variance of the zero-mean i-th activities, adaptive transmission schemes, and electronic ()i ()i 2 constellation as ϑ = Es[|k | ] , iN= 1,2,..., mod , where E[.] warfare. Our comprehensive literature survey [3] shows denotes the mathematical expectation. Then the signal that although this topic has been extensively studied, less power, defined by attention has been paid to modulation classification in NT0 fading channels, and also the utilization of the spatial ()i −12 SNTEstdt00= () [|(;)|]ui ,0, (2) diversity, provided by antenna arrays, in such channels. In ∫0 ()i 2()i this paper, we study these two topics in a systematic way. can be shown to be S00= α ϑ , after substituting (1) into (2). For equiprobable Mi constellation points of the i-th II. SIGNAL, NOISE, AND CHANNEL MODELS ()ii− 1Mi ()2 modulation, obviously one has ϑ = Msim∑m=1||. Note Let st(;u ) represent the noise-free baseband complex ()i 2 i,0 that for PSK and FSK ||1sm = , mM= 1,2,..., i , whereas envelope of the received signal, coming from the i-th ()i 2 in ASK and QAM, ||sm takes different values. modulation format, iN= 1,2,..., , where N is the mod mod In the presence of noise, for the baseband received number of candidates modulations that we are looking at. complex envelope we have The vector ui,0 , which corresponds to the i-th modulation format, denotes the vector of unknown quantities at the rt()= st (;ui,0 )+≤≤ nt (),0 t NT 0 , (3) receiver. In this paper we consider a frequency-flat slowly- where nt() is the complex additive white Gaussian noise varying multipath fading channel with (AWGN) with two-sided power spectral density N ()i N † 1 0 * uikk,0= [αϕ 0 0 {}]s = 1 , where α0 is the channel amplitude, (W/Hz), and the correlation Entn[() ( t+=τ )] N0δτ (), such ____________________________________________________________ that * is the complex conjugate and δ(.) is Dirac delta. 1 As we discuss in the first paragraph after eq. (1), only for frequency shift keying (FSK), the data symbols depend on t. For others such as amplitude shift keying (ASK), phase shift keying not depend upon t. To simplify the notation, we most often drop ()i (PSK), and quadrature amplitude modulation (QAM), sk ’s do this t-dependence, unless otherwise mentioned. 1 of 7 III. DECISION THEORY AND LIKELIHOOD search, to find the ML estimates [18], for each hypothesis. To design the modulation classifier, in order to Moreover, for nested constellations such as BPSK/QPSK, and 16-QAM/64-QAM, the likelihood function in GLRT determine what modulation has been received, out of N mod equally likely candidates, we take the decision-theoretic can take the same numerical values, which in turn leads to approach, which is optimal under certain conditions [2]. incorrect classification [18] [26]. This approach, which works based upon the maximum HLRT is a combination of ALRT and GLRT, in an likelihood (ML) principle, requires the likelihood function attempt to avoid the disadvantages of both techniques, of rt() over the interval 0 ≤≤tNT0 . Using the complex while employing their useful properties. In HLRT, the Gaussian distribution of nt() and for the i-th hypothesis unknown data symbols are considered as random variables Hi (the i-th modulation format), the conditional likelihood and are averaged out, whereas the unknown parameters function of rt(), conditioned on the unknown vector ui,0 , are treated as deterministic unknowns, eventually replaced can be shown to be [2] [5] by their ML estimates. To write the likelihood function, we Ξ=[()|rtu , H ] break ui,0 to two vectors w0 and si such that ii,0 ††† uwsii,0= [] 0 . The vector w0 contains the unknown NT NT † 21002 parameters, whereas s = [...]ss s represents the exp Rer ( t ) s* ( t ; ) dt s ( t ; ) dt , iN12 uuii,0− ,0 (4) unknown data symbols. With this notation, the likelihood NN∫∫00 00 function, conditioned on w , is where Re[.] gives the real part. To derive the likelihood 0 ()i ()i function of rt() from (4), Ξ [()]rt , three techniques are Ξ=Ξ[()|rtwwsss00 ] [()| rt ,ii , H ]( p i| H ii ) d . (9) proposed in the literature, that we discuss in the sequel. ∫ ()i With the ML estimate of w0 for each candidate Once Ξ [()]rt is calculated for all the possible N mod candidate modulations, based on the observed rt() over modulation 0 ≤≤tNT0 , one can make the decision according to ML() i wwˆ i,0 = arg maxΞ [rt ( ) | ] , (10) Choosei as the received modulation w the HLRT likelihood function is eventually given by ifirt=Ξ arg max()i [ ( )]. (5) ()i ()iML 1≤≤iN mod Ξ=ΞHi[()]rt [()| rt wˆ ,0 ]. (11) Obviously our modulation classification is a multiple Averaging over the data symbols in HLRT removes the composite hypothesis testing problem, due to the unknown nested constellations problem of GLRT. However, finding ()i data symbols {}sk , as well as the unknown parameters, the ML estimates of the unknown parameters in HLRT which are α0 and ϕ0 in this paper. Based on our still entails an exhaustive search, which makes its comprehensive literature survey [3] [4], three methods are implementation complex. proposed so far, to handle the unknown quantities: average In this paper, first we derive, in Section IV, closed-form likelihood ratio test (ALRT) [6]-[18], generalized likelihood expressions for the ALRT-based likelihood function in ratio test (GLRT) [19], [20], and hybrid likelihood ratio AWGN and Rayleigh fading channels, for any kind of test (HLRT) [19], [21]-[25]. memoryless modulation, including ASK, PSK, QAM, FSK, The unknown quantities in ALRT are considered as etc. Due to the exponential complexity of these ALRT- random variables, with a certain joint probability density based classifiers, as well as not being applicable to other function (PDF), pH(|uii ), and the likelihood function is types of fading such as Rice, Weibull, Nakagami [1], we derived by averaging the conditional likelihood function then propose a quasi HLRT (QHLRT) approach in Section with respect to it V. In QHLRT, we use non-ML parameter estimators, which are simple yet accurate enough to provide a good Ξ=Ξ()i [()]rt [()| rtuu|u , H ]( p H ) d . (6) Aiiiii∫ classification performance, with much less computational complexity, also applicable to any fading distribution. If the chosen pH(|uii ) is the same as the true PDF, then ALRT is the optimal classifier, i.e., maximizes the Then in Section VI we introduce a multi-antenna classifier, probability of correct classification.
Load more

Recommended publications
  • VHF and UHF Signal Characteristics Observed on a Long Knife-Edge Diffraction Path A
    JOURNAL OF RESEARCH of the National Bureau of Standards- D. Radio Propagatior. Vol. 65D, No. 5, September- Odober 1961 VHF and UHF Signal Characteristics Observed on a Long Knife-Edge Diffraction Path A. P. Barsis and R. S. Kirby (R eceived April 6, 1961) Contribution from Central Radio Propagation Laboratory, National Bureau of Standards, Boulder, Colo. During 1959 and 1960 long-term transmission loss measurements were performed over a 223 kilom eter path in Eastern Colorado using frequencies of 100 and 751 megacycles per second. This path intersects P ikes P eak which forms a knife-edge type obstacle visible from both terminals. The transmission loss measurements have been analyzed in terms of diurnal a nd seaso nal variations in hourly medians and in instan taneous levels. As expected, results show t hat the long-term fading range is substantially less t han expected for t ropospheric seatter paths of comparable length. T ransmission loss levels were in general agreem ent wi t h predicted k ni fe-edge d iffraction propagation when a ll owance is made for rounding of t he knife edge. A technique for est imatin g long-term fading ra nges is presented a nd t he res ults are in good agreement with observations. Short-term variations in some case resemble t he space-wave fadeo uts commonly observed on within- the-horizon paths, a lthough other phe­ nomena may contribute to t he fadin g. Since t he foreground telTain was rough there was no evidence of direct a nd grou nd-refl ected lobe structure.
    [Show full text]
  • Rayleigh Fading Multi-Antenna Channels
    EURASIP Journal on Applied Signal Processing 2002:3, 316–329 c 2002 Hindawi Publishing Corporation Rayleigh Fading Multi-Antenna Channels Alex Grant Institute for Telecommunications Research, University of South Australia, Mawson Lakes Boulevard, Mawson Lakes, SA 5095, Australia Email: [email protected] Received 29 May 2001 Information theoretic properties of flat fading channels with multiple antennas are investigated. Perfect channel knowledge at the receiver is assumed. Expressions for maximum information rates and outage probabilities are derived. The advantages of transmitter channel knowledge are determined and a critical threshold is found beyond which such channel knowledge gains very little. Asymptotic expressions for the error exponent are found. For the case of transmit diversity closed form expressions for the error exponent and cutoff rate are given. The use of orthogonal modulating signals is shown to be asymptotically optimal in terms of information rate. Keywords and phrases: space-time channels, transmit diversity, information theory, error exponents. 1. INTRODUCTION receivers such as the decorrelator and MMSE filter [10]; (b) mitigation of fading effects by averaging over the spatial Wireless access to data networks such as the Internet is ex- properties of the fading process. This is a dual of interleav- pected to be an area of rapid growth for mobile communi- ing techniques which average over the temporal properties cations. High user densities will require very high speed low of the fading process; (c) increased link margins by simply delay links in order to support emerging Internet applica- collecting more of the transmitted energy at the receiver. tions such as voice and video.
    [Show full text]
  • Capacity of Flat and Freq.-Selective Fading Channels Linear Digital Modulation Review
    Lecture 8 - EE 359: Wireless Communications - Winter 2020 Capacity of Flat and Freq.-Selective Fading Channels Linear Digital Modulation Review Lecture Outline • Channel Inversion with Fixed Rate Transmission • Comparison of Fading Channel Capacity under Different Schemes • Capacity of Frequency Selective Fading Channels • Review of Linear Digital Modulation • Performance of Linear Modulation in AWGN 1. Channel Inversion with Fixed Rate Transmission • Suboptimal transmission strategy where fading is inverted to maintain constant re- ceived SNR. • Simplifies system design and is used in CDMA systems for power control. • Capacity with channel inversion greatly reduced over that with optimal adaptation (capacity equals zero in Rayleigh fading). • Truncated inversion: performance greatly improved by inverting above a cutoff γ0. 2. Comparison of Fading Channel Capacity under Different Schemes: • Fading generally decreases channel capacity. • Rate/power adaptation have similar capacity as rate adaptation alone. • Rate adaptation alone has same capacity as no adaptation (RX CSI only) but rate adaptation is more practical due to complexity of ML decoding over long blocklengths that experience all fading values. This ML decoding is necesssary to achieve capacity in the RX CSI only case. • Truncated channel inversion is more practical than rate adaptation, with significant capacity gain over full channel inversion, which has zero capacity in Rayleigh fading. 3. Capacity of Frequency Selective Fading Channels • Capacity for time-invariant frequency-selective fading channels is a \water-filling” of power over frequency. • For time-varying ISI channels, capacity is unknown in general. Approximate by di- viding up the bandwidth subbands of width equal to the coherence bandwidth (same premise as multicarrier modulation) with independent fading in each subband.
    [Show full text]
  • Fading Channels: Capacity, BER and Diversity
    Fading Channels: Capacity, BER and Diversity Master Universitario en Ingenier´ıade Telecomunicaci´on I. Santamar´ıa Universidad de Cantabria Introduction Capacity BER Diversity Conclusions Contents Introduction Capacity BER Diversity Conclusions Fading Channels: Capacity, BER and Diversity 0/48 Introduction Capacity BER Diversity Conclusions Introduction I We have seen that the randomness of signal attenuation (fading) is the main challenge of wireless communication systems I In this lecture, we will discuss how fading affects 1. The capacity of the channel 2. The Bit Error Rate (BER) I We will also study how this channel randomness can be used or exploited to improve performance diversity ! Fading Channels: Capacity, BER and Diversity 1/48 Introduction Capacity BER Diversity Conclusions General communication system model sˆ[n] bˆ[n] b[n] s[n] Channel Channel Source Modulator Channel ⊕ Demod. Encoder Decoder Noise I The channel encoder (FEC, convolutional, turbo, LDPC ...) adds redundancy to protect the source against errors introduced by the channel I The capacity depends on the fading model of the channel (constant channel, ergodic/block fading), as well as on the channel state information (CSI) available at the Tx/Rx Let us start reviewing the Additive White Gaussian Noise (AWGN) channel: no fading Fading Channels: Capacity, BER and Diversity 2/48 Introduction Capacity BER Diversity Conclusions AWGN Channel I Let us consider a discrete-time AWGN channel y[n] = hs[n] + r[n] where r[n] is the additive white Gaussian noise, s[n] is the
    [Show full text]
  • 2 the Wireless Channel
    CHAPTER 2 The wireless channel A good understanding of the wireless channel, its key physical parameters and the modeling issues, lays the foundation for the rest of the book. This is the goal of this chapter. A defining characteristic of the mobile wireless channel is the variations of the channel strength over time and over frequency. The variations can be roughly divided into two types (Figure 2.1): • Large-scale fading, due to path loss of signal as a function of distance and shadowing by large objects such as buildings and hills. This occurs as the mobile moves through a distance of the order of the cell size, and is typically frequency independent. • Small-scale fading, due to the constructive and destructive interference of the multiple signal paths between the transmitter and receiver. This occurs at the spatialscaleoftheorderofthecarrierwavelength,andisfrequencydependent. We will talk about both types of fading in this chapter, but with more emphasis on the latter. Large-scale fading is more relevant to issues such as cell-site planning. Small-scale multipath fading is more relevant to the design of reliable and efficient communication systems – the focus of this book. We start with the physical modeling of the wireless channel in terms of elec- tromagnetic waves. We then derive an input/output linear time-varying model for the channel, and define some important physical parameters. Finally, we introduce a few statistical models of the channel variation over time and over frequency. 2.1 Physical modeling for wireless channels Wireless channels operate through electromagnetic radiation from the trans- mitter to the receiver.
    [Show full text]
  • Distortion Exponent of Parallel Fading Channels
    Distortion Exponent of Parallel Fading Channels Deniz Gunduz, Elza Erkip Department of Electrical and Computer Engineering, Polytechnic University, Brooklyn, NY 11201, USA [email protected], [email protected] Abstract— We consider the end-to-end distortion achieved by the fading process. Lack of channel state information at the transmitting a continuous amplitude source over M parallel, transmitter prevents the design of a channel code that achieves independent quasi-static fading channels. We analyze the high the instantaneous channel capacity and requires a code that SNR expected distortion behavior characterized by the distortion exponent. We first give an upper bound for the distortion performs well on the average. We aim to design a joint source- exponent in terms of the bandwidth ratio between the channel channel code that achieves the minimum expected end-to-end and the source assuming the availability of the channel state distortion. Our main focus is the high SNR behavior of this information at the transmitter. Then we propose joint source- expected distortion (ED). This behavior is characterized by the channel coding schemes based on layered source coding and distortion exponent denoted by ¢ and defined as multiple rate channel coding. We show that the upper bound is tight for large and small bandwidth ratios. For the rest, we log ED provide the best known distortion exponents in the literature. ¢ = ¡ lim : (1) SNR!1 log SNR By suitably scaling the bandwidth ratio, our results would also apply to block fading channels. When we consider digital transmission strategies that first compress the source and then transmit over the channel at I.
    [Show full text]
  • On Routing in Random Rayleigh Fading Networks Martin Haenggi, Senior Member, IEEE
    IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 4, NO. 4, JULY 2005 1553 On Routing in Random Rayleigh Fading Networks Martin Haenggi, Senior Member, IEEE Abstract—This paper addresses the routing problem for large loss probabilities increase with the number of hops (unless the wireless networks of randomly distributed nodes with Rayleigh transmit power is adapted). fading channels. First, we establish that the distances between To overcome some of these limitations of the “disk model,” neighboring nodes in a Poisson point process follow a generalized Rayleigh distribution. Based on this result, it is then shown that, we employ a simple Rayleigh fading link model that relates given an end-to-end packet delivery probability (as a quality of transmit power, large-scale path loss, and the success of a service requirement), the energy benefits of routing over many transmission. The end-to-end packet delivery probability over short hops are significantly smaller than for deterministic network a multihop route is the product of the link-level reception models that are based on the geometric disk abstraction. If the probabilities. permissible delay for short-hop routing and long-hop routing is the same, it turns out that routing over fewer but longer hops may While fading has been considered in the context of packet even outperform nearest-neighbor routing, in particular for high networks [16], [17], its impact on the network (and higher) end-to-end delivery probabilities. layers is largely an open problem. This paper attempts to shed Index Terms—Ad hoc networks, communication systems, fading some light on this cross-layer issue by analyzing the perfor- channels, Poisson processes, probability, routing.
    [Show full text]
  • Kahn Communications, Inc. 425 Merrick Avenue Westbury, New York 11590 (516) 2222221
    KAHN COMMUNICATIONS, INC. 425 MERRICK AVENUE WESTBURY, NEW YORK 11590 (516) 2222221 THE "WGAS EFFECT" AND THE FUTURE OF AM RADIO In the history of broadcasting a number of "Effects" have dramatically impacted on broadcasting. For example, the "Capture Effect" and the "Multipath Effect" of FM, and earlier "Radio Luxemburg Effect" helped shape broadcasting history. More recently, "Clicks and Pops", "Platform Motion", and "Rain Noise" have influenced the path of AM Stereo. Remember when the Magnavox system was selected by the FCC as the standard in 1980 and the "Click and Pop" effect was discovered. By 1982 it became clear that this "Click and Pop" problem made it essential that the FCC revisit its decision. There is now a new phenomenon which we propose to name the "WGAS Effect" because it was first described in the "Open Mike" section of the September 7, 1987 issue of "Broadcasting" by Mr. Glenn Mace, President of WGAS, South Gastonia, North Carolina. It is essential that all AM broadcasters carefully read this short letter because the very future of AM radio may depend upon the industries knowledge of its contents. It should be stressed that WGAS does not, and cannot, endorse our stereo system as they have never used it. But, nevertheless, we are most appreciative that Mr. Mace has taken the time and effort to make his observations public on this important matter. More will follow re the "WGAS Effect" and how it impacts on all stations, large and small, which must serve listeners in their 25 my/meter contour and beyond. age.
    [Show full text]
  • BER Analysis of Digital Broadcasting System Through AWGN and Rayleigh Channels
    International Journal of Engineering and Advanced Technology (IJEAT) ISSN: 2249 – 8958, Volume-2 Issue-1, October 2012 BER Analysis of Digital Broadcasting System Through AWGN and Rayleigh Channels P.Ravi Kumar, V.Venkata Rao., M.Srinivasa Rao. transmission system based on Eureka-147 standard [1]. The Abstract — Radio broadcasting technology in this era of design consists of energy dispersal scrambler, QPSK symbol compact disc is expected to deliver high quality audio mapping, convolutional encoder (FEC), D-QPSK modulator programmes in mobile environment. The Eureka-147 Digital with frequency interleaving and OFDM signal generator Audio Broadcasting (DAB) system with coded OFDM (IFFT) in the transmitter side and in the receiver technology accomplish this demand by making receivers highly corresponding inverse operations is carried out along with robust against effects of multipath fading environment. In this fine time synchronization [4] using phase reference symbol. paper, we have analysed the performance of DAB system conforming to the parameters established by the ETSI (EN 300 DAB transmission mode-II is implemented. A frame based 401) using time and frequency interleaving, concatenated processing is used in this work. Bit error rate (BER) has been Bose-Chaudhuri- Hocquenghem coding and convolutional considered as the performance index in all analysis. The coding method in different transmission channels. The results analysis has been carried out with simulation studies under show that concatenated channel coding improves the system MATLAB environment. performance compared to convolutional coding. Following this introduction the remaining part of the paper is organized as follows. Section II introduces the DAB Keywords- DAB, OFDM, Multipath effect, concatenated system standard.
    [Show full text]
  • Performance Analysis of MIMO Spatial Multiplexing Using Different Antenna Configurations and Modulation Technique in Rician Channel Hardeep Singh, Lavish Kansal
    International Journal of Scientific & Engineering Research, Volume 5, Issue 6, June-2014 34 ISSN 2229-5518 Performance Analysis of MIMO Spatial Multiplexing using different Antenna Configurations and Modulation Technique in Rician Channel Hardeep Singh, Lavish Kansal Abstract— MIMO systems which employs multiple antennas at the transmitter as well as at the receiver side is the key technique to be employed in next generation wireless communication systems. MIMO systems provide various benefits such as Spatial Diversity, Spatial Multiplexing to improve the system performance. In this paper the MIMO SM system is analysed for different antenna configurations (2×2, 3×3, 4×4) in Rician channel. The performance of the MIMO SM system is investigated for higher order modulation schemes (M-PSK, M-QAM) and Zero Forcing equalizer is employed at the receiving side. The simulation results points that if antenna configurations are shifted from 2×2 to 3×3 configuration, an improvement of 0 to 2.9 db in SNR is being noted and an improvement of 0 to 2.9 db is visualized if antenna configurations are changed from 3×3 to 4×4 configuration. Index Terms— Multiple Input Multiple Output (MIMO), Zero Forcing (ZF), Spatial Multiplexing (SM), M-ary Phase Shift Keying (M-PSK) M-ary Quadrature Amplitude Modulation (M-QAM), Bit Error Rate (BER), Signal to Noise Ratio (SNR). —————————— —————————— 1 INTRODUCTION IMO (Multiple Input Multiple Output) systems employ higher extend, but the benefits of beamforming technique are multiple antennas at both the ends of a communication limited in such environments. Mlink. The MIMO systems provide various applications In order to obtain channel state information at receiving side, such as beamforming (increasing the average SNR at receiver the pilot bits are sent along with the transmitted sequence to side), Spatial Diversity (to achieve good BER at low SNR), Spa- estimate the channel state.
    [Show full text]
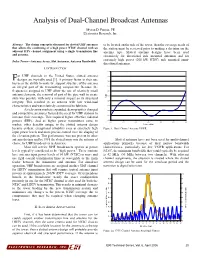
  • Analysis of Dual-Channel Broadcast Antennas
    Analysis of Dual-Channel Broadcast Antennas Myron D. Fanton, PE Electronics Research, Inc. Abstract—The design concept is discussed for slotted UHF antennas to be located on the side of the tower, then the coverage needs of that allows the combining of a high power NTSC channel with an the station must be reviewed prior to making a decision on the adjacent DTV channel assignment using a single transmission line antenna type. Slotted antenna designs have been used and antenna. extensively for directional side mounted antennas and for extremely high power (200 kW NTSC) side mounted omni- Index Terms—Antenna Array, Slot Antennas, Antenna Bandwidth. directional antennas. I. INTRODUCTION 1.10 or UHF channels in the United States, slotted antenna 1.09 designs are typically used [1]. A primary factor in their use F 1.08 has been the ability to make the support structure of the antenna an integral part of the transmitting components. Because the 1.07 frequencies assigned to UHF allow the use of relatively small 1.06 antenna elements, the removal of part of the pipe wall to create 1.05 slots was possible with only a minimal impact an its structural VSWR integrity. This resulted in an antenna with low wind-load 1.04 characteristics and was relatively economical to fabricate. 1.03 As television markets expanded, demographics changed 1.02 and competitive pressures fostered the need for UHF stations to increase their coverage. This required higher effective radiated 1.01 1.00 powers (ERP). And as higher power transmitters came to 572 574 576 578 580 582 584 market, other benefits unique to the slotted antenna design Frequency (MHz) became evident: exceptional reliability even at extremely high Figure 1: Dual Channel Antenna VSWR input power levels and more precise control over the shaping of the elevation pattern.
    [Show full text]
  • Long-Wave and Medium-Wave Propagation
    ~EMGINEERING TRAINING SUPPLEMENT No. 10 LONG-WAVE AND MEDIUM-WAVE PROPAGATION BRITISH BROADCASTING CORPORATION LONDON 1957 ENGINEERING TRAINING SUPPLEMENT No. 10 LONG-WAVE AND MEDIUM-WAVE PROPAGATION Prepared by the Engineering Training Department from an original manuscript by H. E. FARROW, Grad.1.E.E. Issued by THE BBC ENGINEERING TRAINING DEPARTMENT 1957 ACKNOWLEDGMENTS Fig. 2 is based upon a curve given by H. P. Williams in 'Antenna Theory and Design', published by Sir Isaac Pitrnan and Sons Ltd. Figs. 5, 6, 7, 8 and 9 are based upon curves prepared by the C.C.I.R. CONTENTS ACKNOWLEDGMENTS... ... INTRODUCTION ... ... ... AERIALS ... ... ... ... GROUND-WAVEPROPAGATION ... GEOLOGICALCORRELATION ... PROPAGATIONCURVES ... ... RECOVERYAND LOSS EFFECTS ... MIXED-PATHPROPAGATION ... SYNCHRONISED. GROUP WORKING LOW-POWERINSTALLATIONS ... IONOSPHERICREFLECTION ... FADING ... ... ... ... REDUCTIONOF SERVICEAREA BY SKYWAVE ... LONG-RANGEINTERFERENCE BY SKYWAVE ... APPENDIXI ... ... ... ... ... REFERENCES ... ... ... ... ... LONG-WAVE AND MEDIUM-WAVE PROPAGATION The general purpose of this Supplement is to explain the main features of propagation at low and medium frequencies i.e. 30-3000 kc/s, and in particular in the bands used for broadcasting viz. 150-285 kc/s and 525-1605 kc/s. In these bands, the signal at the receiver may have two components: they are (a) a ground wave, i.e. one that follows ground contours (b) an ionspheric wave (sky wave) which is reflected from an ionised layer under certain conditions. In the vicinity of the transmitter, the ground wave is the predominant component, and for domestic broadcasting, the service ideally would be provided by the ground wave only. In fact the limit to the service area is often set by interference from the sky wave.
    [Show full text]