DOCSLIB.ORG

Also Known As a Minkowski Diagram) Is a Tool That Can Used to Graphically Describe Complex Problems in Special Relativity

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Also Known As a Minkowski Diagram) Is a Tool That Can Used to Graphically Describe Complex Problems in Special Relativity Spacetime Diagrams Lab Exercise The spacetime diagram (also known as a Minkowski diagram) is a tool that can used to graphically describe complex problems in special relativity. In many cases, with a properly drawn spacetime diagram you can estimate an answer without working any complex problems. 1. Spacetime Diagrams and Events: A spacetime diagram is a tool that can show how physical events relate to one another. Making measurements of time and distance in relativity can be very complex so we have to use clear definitions. An event is is a physical occurrence that happens at a definite place in space, and a definite instant in time. For our purposes, we will restrict ourselves to 1D motion, so an event will be defined by a pair of coordinate, the time, t, and position, x. In a spacetime diagram we plot the time along the vertical axis, and the position along the horizontal axis. This will be different the motion diagrams you used in your first physics courses where the axes are usually swapped. In this orientation, we can represent time as moving upward to show the sequence of events. Open the spacetime diagram program. At the bottom there is a slider called beta, slide this all the way to zero for the first exercise. On the right, there is are checkboxes for a set of events from Event A to Event F. Click the checkbox to activate one of the events. You can change the coordinates of the event by entering the values into the text boxes under the Home Frame heading (ignore the Other Frame for the moment.) Or you can click and drag the event to move it to a new set of coordinate values. When an event is selected, the program will show the coordinate traces illustrating how the coordinate values are determined from the axes. A note about units: the time and position axes are scaled with the same units, in this case time. You can think of the x-position values as representing the distance in light-seconds, the distance that light can travel in one second. Specific units have been left out so that the diagram can represent light-seconds, light-minutes, light-years, or whatever scale is appropriate to a given problem. 2. World-lines: We can use a spacetime diagram to show the motion of object. Consider an object moving at the speed of light, it moves 1 light-second (or ls) for each 1 second of time. Note that the diagram has a yellow dotted line drawn with a slope of 1 that represents the speed of light (this is why we use light-seconds and seconds instead of meters and seconds on a spacetime diagram.) The speed of light is particularly important in special relativity, so it is convenient to display it on the spacetime diagram. a) Now consider an object moving ½ the speed of light, or 0.5c. How many light-seconds will it move each second of time? b) Now think of the object having a blinking light on it, that blinks every second (as measured by a stationary observer, don't make it too complicated yet.) If the object starts at the origin at t = 0, and is moving to the right, where will it be at 1s? c) In the spacetime diagram program, place an event for each light blink as the object moves in the +x direction. Think of a line connecting each of the evens. What is the slope of this line in the spacetime diagram? d) If the object was moving at 0.8 c, what would be the slope of the line? e) A world-line is a line showing the position of the object as a function of time. The velocity of the object is 1/slope of the world-line on the spacetime diagram. If the object is stationary at x = 2 ls, what will its world-line look like? 3. Spacetime Interval and Non-Euclidean nature of spacetime. In Euclidean geometry (flat, parallel lines always stay parallel, angles of a triangle add up to 180°) we define the distance d between two points as d 2 = x2 y2 , where x is the difference between the x coordinates of the two points, and y is the differences between the y coordinates of the two points. The distance is invariant under coordinate transformations, i.e. any other coordinate system will give the two points different values for the x and y coordinates of the two points, but the distance will always come out the same. a) On diagram 1 below, sketch the set of all points for which d =2 . What shape do these points make? b) On the diagram 2 below, there is a rotated coordinate system. Place a point at x =1, y = 3 in the unrotated coordinate system. What are the coordinates of the point in the rotated (x', y') coordinate system? c) Calculate the distance between the origin and point in each reference frame. You should get the same result for each. Diagram 1 Diagram 2 Spacetime, is non-Euclidean and we must define a new invariant quantity for measuring the “distance” between two points, the spacetime interval: s2 = t 2− x2 . Note that we are using time units for both position and time (think of Δ x = 1s as 1 light-second, the distance that light travels in one second.) d) The spacetime diagram program has a tool for calculating the spacetime interval between two events. Click the “Measure Δ s “ button. Then click and drag inside the diagram. A line with two arrows (and coordinate traces on the endpoints) will show how the spacetime interval is calculated between two points. The text fields will show the Δ t ,Δ x , Δ s2 , and Δ s values for the two points chosen. The spacetime interval calculator should snap to the origin, or any events that are already drawn in the diagram to make it easier. e) One the spacetime diagram place the first point of the Δ s calculator on the origin and find the points for which Δ s=2s . Move events to mark those points. Try to cover a fairly large range of x-values, perhaps every 1 light-second along x. Take a snapshot of the screen and put it in a document. f) What shape does this make? 4. World-lines and the t' time axis : Since an object moving at constant velocity is in an inertial frame, we can say that the world-line of each object is the position of the origin for a coordinate system being carried by each moving object. The origin marks where x ' = 0 in the other coordinate system, and therefore the world-line becomes the t' axis for the moving object. Along the t' axis then, x ' = 0 , and therefore t ' = s as measured from the origin along the t' axis. This gives us the scaling for the t' axis. a) Keep the curve from the previous exercise for s=2s . Adjust the slider for beta below the diagram. Increasing beta, increases the relative velocity of an object moving along the t' axis. Where this curve intersects the t' axis for each object shows us where t ' =2s . Note that as we adjust the value of beta, the tic mark for t '=2s always coincides with the curve of events drawn in the previous exercise. b) What happens to the scaling of the t' axis as an object's velocity increases? c) What happens as the velocity approaches the speed of light? 5. Two-observer Spacetime Diagrams: We can use a diagram with two coordinate systems setup to describe a scenario from the perspective of two observers in inertial reference frames. The first step is to create the coordinate system for the observer moving to the right with respect to the first. By convention, the reference frame of an observer moving to the right, the Other Frame. The Home Frame is the one that measures the observer moving to the right (which would be moving to the left from the perspective of an observer moving in the Other Frame) a) Set the slider to = 0.6c . We can use an alternate to the hyperbola from parts 1and 2 to calibrate the scale for the t' axis. 1 Use the relationship Δ t = γ Δ t ' , where = . 1−2 b) Calculate for our example and check that it agrees with the value shown next to the slider: c) Now place an event on the world-line of the object at t '=1s tic-mark. Read off the t coordinate of the event from the home frame spacetime coordinates: d) Calculate t = t ' , with Δ t ' = 1s and compare to the t coordinate of the event: Drawing the x'-axis. To keep the speed of light constant to all observers in inertial reference frames, the x' – axis rotates up from x-axis the same angle as the t' axis rotates away from the t -axis. Essentially, the x' axis will have a slope of , while the t' axis will have a slope of 1/ . We can use a similar means to scale the x' axis as well, Δ x = γ Δ x ' e) Place an event on the x '=1 tic mark. Read off the x coordinate of the event from the home frame spacetime coordinates: f) Check that it agrees with x = x' Reading Event Coordinates in both frames: When you select an event, the coordinate traces that for the event are parallel to the t and x coordinate axes, which is how we normally read coordinates off of a graph.
Load more

Recommended publications
  • A Mathematical Derivation of the General Relativistic Schwarzschild
    A Mathematical Derivation of the General Relativistic Schwarzschild Metric An Honors thesis presented to the faculty of the Departments of Physics and Mathematics East Tennessee State University In partial fulfillment of the requirements for the Honors Scholar and Honors-in-Discipline Programs for a Bachelor of Science in Physics and Mathematics by David Simpson April 2007 Robert Gardner, Ph.D. Mark Giroux, Ph.D. Keywords: differential geometry, general relativity, Schwarzschild metric, black holes ABSTRACT The Mathematical Derivation of the General Relativistic Schwarzschild Metric by David Simpson We briefly discuss some underlying principles of special and general relativity with the focus on a more geometric interpretation. We outline Einstein’s Equations which describes the geometry of spacetime due to the influence of mass, and from there derive the Schwarzschild metric. The metric relies on the curvature of spacetime to provide a means of measuring invariant spacetime intervals around an isolated, static, and spherically symmetric mass M, which could represent a star or a black hole. In the derivation, we suggest a concise mathematical line of reasoning to evaluate the large number of cumbersome equations involved which was not found elsewhere in our survey of the literature. 2 CONTENTS ABSTRACT ................................. 2 1 Introduction to Relativity ...................... 4 1.1 Minkowski Space ....................... 6 1.2 What is a black hole? ..................... 11 1.3 Geodesics and Christoffel Symbols ............. 14 2 Einstein’s Field Equations and Requirements for a Solution .17 2.1 Einstein’s Field Equations .................. 20 3 Derivation of the Schwarzschild Metric .............. 21 3.1 Evaluation of the Christoffel Symbols .......... 25 3.2 Ricci Tensor Components .................
    [Show full text]
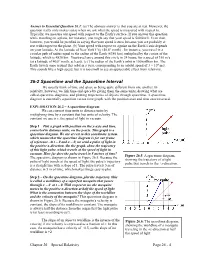
  • 26-2 Spacetime and the Spacetime Interval We Usually Think of Time and Space As Being Quite Different from One Another
    Answer to Essential Question 26.1: (a) The obvious answer is that you are at rest. However, the question really only makes sense when we ask what the speed is measured with respect to. Typically, we measure our speed with respect to the Earth’s surface. If you answer this question while traveling on a plane, for instance, you might say that your speed is 500 km/h. Even then, however, you would be justified in saying that your speed is zero, because you are probably at rest with respect to the plane. (b) Your speed with respect to a point on the Earth’s axis depends on your latitude. At the latitude of New York City (40.8° north) , for instance, you travel in a circular path of radius equal to the radius of the Earth (6380 km) multiplied by the cosine of the latitude, which is 4830 km. You travel once around this circle in 24 hours, for a speed of 350 m/s (at a latitude of 40.8° north, at least). (c) The radius of the Earth’s orbit is 150 million km. The Earth travels once around this orbit in a year, corresponding to an orbital speed of 3 ! 104 m/s. This sounds like a high speed, but it is too small to see an appreciable effect from relativity. 26-2 Spacetime and the Spacetime Interval We usually think of time and space as being quite different from one another. In relativity, however, we link time and space by giving them the same units, drawing what are called spacetime diagrams, and plotting trajectories of objects through spacetime.
    [Show full text]
  • Thermodynamics of Spacetime: the Einstein Equation of State
    gr-qc/9504004 UMDGR-95-114 Thermodynamics of Spacetime: The Einstein Equation of State Ted Jacobson Department of Physics, University of Maryland College Park, MD 20742-4111, USA [email protected] Abstract The Einstein equation is derived from the proportionality of entropy and horizon area together with the fundamental relation δQ = T dS connecting heat, entropy, and temperature. The key idea is to demand that this relation hold for all the local Rindler causal horizons through each spacetime point, with δQ and T interpreted as the energy flux and Unruh temperature seen by an accelerated observer just inside the horizon. This requires that gravitational lensing by matter energy distorts the causal structure of spacetime in just such a way that the Einstein equation holds. Viewed in this way, the Einstein equation is an equation of state. This perspective suggests that it may be no more appropriate to canonically quantize the Einstein equation than it would be to quantize the wave equation for sound in air. arXiv:gr-qc/9504004v2 6 Jun 1995 The four laws of black hole mechanics, which are analogous to those of thermodynamics, were originally derived from the classical Einstein equation[1]. With the discovery of the quantum Hawking radiation[2], it became clear that the analogy is in fact an identity. How did classical General Relativity know that horizon area would turn out to be a form of entropy, and that surface gravity is a temperature? In this letter I will answer that question by turning the logic around and deriving the Einstein equation from the propor- tionality of entropy and horizon area together with the fundamental relation δQ = T dS connecting heat Q, entropy S, and temperature T .
    [Show full text]
  • Chapter 5 the Relativistic Point Particle
    Chapter 5 The Relativistic Point Particle To formulate the dynamics of a system we can write either the equations of motion, or alternatively, an action. In the case of the relativistic point par- ticle, it is rather easy to write the equations of motion. But the action is so physical and geometrical that it is worth pursuing in its own right. More importantly, while it is difficult to guess the equations of motion for the rela- tivistic string, the action is a natural generalization of the relativistic particle action that we will study in this chapter. We conclude with a discussion of the charged relativistic particle. 5.1 Action for a relativistic point particle How can we find the action S that governs the dynamics of a free relativis- tic particle? To get started we first think about units. The action is the Lagrangian integrated over time, so the units of action are just the units of the Lagrangian multiplied by the units of time. The Lagrangian has units of energy, so the units of action are L2 ML2 [S]=M T = . (5.1.1) T 2 T Recall that the action Snr for a free non-relativistic particle is given by the time integral of the kinetic energy: 1 dx S = mv2(t) dt , v2 ≡ v · v, v = . (5.1.2) nr 2 dt 105 106 CHAPTER 5. THE RELATIVISTIC POINT PARTICLE The equation of motion following by Hamilton’s principle is dv =0. (5.1.3) dt The free particle moves with constant velocity and that is the end of the story.
    [Show full text]
  • Physics 200 Problem Set 7 Solution Quick Overview: Although Relativity Can Be a Little Bewildering, This Problem Set Uses Just A
    Physics 200 Problem Set 7 Solution Quick overview: Although relativity can be a little bewildering, this problem set uses just a few ideas over and over again, namely 1. Coordinates (x; t) in one frame are related to coordinates (x0; t0) in another frame by the Lorentz transformation formulas. 2. Similarly, space and time intervals (¢x; ¢t) in one frame are related to inter- vals (¢x0; ¢t0) in another frame by the same Lorentz transformation formu- las. Note that time dilation and length contraction are just special cases: it is time-dilation if ¢x = 0 and length contraction if ¢t = 0. 3. The spacetime interval (¢s)2 = (c¢t)2 ¡ (¢x)2 between two events is the same in every frame. 4. Energy and momentum are always conserved, and we can make e±cient use of this fact by writing them together in an energy-momentum vector P = (E=c; p) with the property P 2 = m2c2. In particular, if the mass is zero then P 2 = 0. 1. The earth and sun are 8.3 light-minutes apart. Ignore their relative motion for this problem and assume they live in a single inertial frame, the Earth-Sun frame. Events A and B occur at t = 0 on the earth and at 2 minutes on the sun respectively. Find the time di®erence between the events according to an observer moving at u = 0:8c from Earth to Sun. Repeat if observer is moving in the opposite direction at u = 0:8c. Answer: According to the formula for a Lorentz transformation, ³ u ´ 1 ¢tobserver = γ ¢tEarth-Sun ¡ ¢xEarth-Sun ; γ = p : c2 1 ¡ (u=c)2 Plugging in the numbers gives (notice that the c implicit in \light-minute" cancels the extra factor of c, which is why it's nice to measure distances in terms of the speed of light) 2 min ¡ 0:8(8:3 min) ¢tobserver = p = ¡7:7 min; 1 ¡ 0:82 which means that according to the observer, event B happened before event A! If we reverse the sign of u then 2 min + 0:8(8:3 min) ¢tobserver 2 = p = 14 min: 1 ¡ 0:82 2.
    [Show full text]
  • Einstein's Gravitational Field
    Einstein’s gravitational field Abstract: There exists some confusion, as evidenced in the literature, regarding the nature the gravitational field in Einstein’s General Theory of Relativity. It is argued here that this confusion is a result of a change in interpretation of the gravitational field. Einstein identified the existence of gravity with the inertial motion of accelerating bodies (i.e. bodies in free-fall) whereas contemporary physicists identify the existence of gravity with space-time curvature (i.e. tidal forces). The interpretation of gravity as a curvature in space-time is an interpretation Einstein did not agree with. 1 Author: Peter M. Brown e-mail: [email protected] 2 INTRODUCTION Einstein’s General Theory of Relativity (EGR) has been credited as the greatest intellectual achievement of the 20th Century. This accomplishment is reflected in Time Magazine’s December 31, 1999 issue 1, which declares Einstein the Person of the Century. Indeed, Einstein is often taken as the model of genius for his work in relativity. It is widely assumed that, according to Einstein’s general theory of relativity, gravitation is a curvature in space-time. There is a well- accepted definition of space-time curvature. As stated by Thorne 2 space-time curvature and tidal gravity are the same thing expressed in different languages, the former in the language of relativity, the later in the language of Newtonian gravity. However one of the main tenants of general relativity is the Principle of Equivalence: A uniform gravitational field is equivalent to a uniformly accelerating frame of reference. This implies that one can create a uniform gravitational field simply by changing one’s frame of reference from an inertial frame of reference to an accelerating frame, which is rather difficult idea to accept.
    [Show full text]
  • Theory of Relativity
    Christian Bar¨ Theory of Relativity Summer Term 2013 OTSDAM P EOMETRY IN G Version of August 26, 2013 Contents Preface iii 1 Special Relativity 1 1.1 Classical Kinematics ............................... 1 1.2 Electrodynamics ................................. 5 1.3 The Lorentz group and Minkowski geometry .................. 7 1.4 Relativistic Kinematics .............................. 20 1.5 Mass and Energy ................................. 36 1.6 Closing Remarks about Special Relativity .................... 41 2 General Relativity 43 2.1 Classical theory of gravitation .......................... 43 2.2 Equivalence Principle and the Einstein Field Equations ............. 49 2.3 Robertson-Walker spacetime ........................... 55 2.4 The Schwarzschild solution ............................ 66 Bibliography 77 Index 79 i Preface These are the lecture notes of an introductory course on relativity theory that I gave in 2013. Ihe course was designed such that no prior knowledge of differential geometry was required. The course itself also did not introduce differential geometry (as it is often done in relativity classes). Instead, students unfamiliar with differential geometry had the opportunity to learn the subject in another course precisely set up for this purpose. This way, the relativity course could concentrate on its own topic. Of course, there is a price to pay; the first half of the course was dedicated to Special Relativity which does not require much mathematical background. Only the second half then deals with General Relativity. This gave the students time to acquire the geometric concepts. The part on Special Relativity briefly recalls classical kinematics and electrodynamics empha- sizing their conceptual incompatibility. It is then shown how Minkowski geometry is used to unite the two theories and to obtain what we nowadays call Special Relativity.
    [Show full text]
  • Modified Gravity and Thermodynamics of Time-Dependent Wormholes At
    Journal of High Energy Physics, Gravitation and Cosmology, 2017, 3, 708-714 http://www.scirp.org/journal/jhepgc ISSN Online: 2380-4335 ISSN Print: 2380-4327 Modified fR( ) Gravity and Thermodynamics of Time-Dependent Wormholes at Event Horizon Hamidreza Saiedi Department of Physics, Florida Atlantic University, Boca Raton, FL, USA How to cite this paper: Saiedi, H. (2017) Abstract Modified f(R) Gravity and Thermodynam- ics of Time-Dependent Wormholes at In the context of modified fR( ) gravity theory, we study time-dependent Event Horizon. Journal of High Energy wormhole spacetimes in the radiation background. In this framework, we at- Physics, Gravitation and Cosmology, 3, 708-714. tempt to generalize the thermodynamic properties of time-dependent worm- https://doi.org/10.4236/jhepgc.2017.34053 holes in fR( ) gravity. Finally, at event horizon, the rate of change of total Received: August 1, 2017 entropy has been discussed. Accepted: October 20, 2017 Published: October 23, 2017 Keywords Copyright © 2017 by author and fR( ) Gravity, Time-Dependent Wormholes, Thermodynamics, Scientific Research Publishing Inc. Event Horizon This work is licensed under the Creative Commons Attribution International License (CC BY 4.0). http://creativecommons.org/licenses/by/4.0/ 1. Introduction Open Access Wormholes, short cuts between otherwise distant or unconnected regions of the universe, have become a popular research topic since the influential paper of Morris and Thorne [1]. Early work was reviewed in the book of Visser [2]. The Morris-Thorne (MT) study was restricted to static, spherically symmetric space-times, and initially there were various attempts to generalize the definition of wormhole by inserting time-dependent factors into the metric.
    [Show full text]
  • Post-Newtonian Approximations and Applications
    Monash University MTH3000 Research Project Coming out of the woodwork: Post-Newtonian approximations and applications Author: Supervisor: Justin Forlano Dr. Todd Oliynyk March 25, 2015 Contents 1 Introduction 2 2 The post-Newtonian Approximation 5 2.1 The Relaxed Einstein Field Equations . 5 2.2 Solution Method . 7 2.3 Zones of Integration . 13 2.4 Multi-pole Expansions . 15 2.5 The first post-Newtonian potentials . 17 2.6 Alternate Integration Methods . 24 3 Equations of Motion and the Precession of Mercury 28 3.1 Deriving equations of motion . 28 3.2 Application to precession of Mercury . 33 4 Gravitational Waves and the Hulse-Taylor Binary 38 4.1 Transverse-traceless potentials and polarisations . 38 4.2 Particular gravitational wave fields . 42 4.3 Effect of gravitational waves on space-time . 46 4.4 Quadrupole formula . 48 4.5 Application to Hulse-Taylor binary . 52 4.6 Beyond the Quadrupole formula . 56 5 Concluding Remarks 58 A Appendix 63 A.1 Solving the Wave Equation . 63 A.2 Angular STF Tensors and Spherical Averages . 64 A.3 Evaluation of a 1PN surface integral . 65 A.4 Details of Quadrupole formula derivation . 66 1 Chapter 1 Introduction Einstein's General theory of relativity [1] was a bold departure from the widely successful Newtonian theory. Unlike the Newtonian theory written in terms of fields, gravitation is a geometric phenomena, with space and time forming a space-time manifold that is deformed by the presence of matter and energy. The deformation of this differentiable manifold is characterised by a symmetric metric, and freely falling (not acted on by exter- nal forces) particles will move along geodesics of this manifold as determined by the metric.
    [Show full text]
  • Descriptions of Relativistic Dynamics with World Line Condition
    quantum reports Article Descriptions of Relativistic Dynamics with World Line Condition Florio Maria Ciaglia 1 , Fabio Di Cosmo 2,3,* , Alberto Ibort 2,3 and Giuseppe Marmo 4,5 1 Max-Planck-Institut für Mathematik in den Naturwissenschaften, Inselstraße 22, 04103 Leipzig, Germany; [email protected] 2 Dep.to de Matematica, Univ. Carlos III de Madrid. Av. da de la Universidad, 30, 28911 Leganes, Madrid, Spain; [email protected] 3 ICMAT, Instituto de Ciencias Matematicas (CSIC-UAM-UC3M-UCM), Nicolás Cabrera, 13-15, Campus de Cantoblanco, UAM, 28049 Madrid, Spain 4 INFN-Sezione di Napoli, Complesso Universitario di Monte S. Angelo. Edificio 6, via Cintia, 80126 Napoli, Italy; [email protected] 5 Dipartimento di Fisica “E. Pancini”, Università di Napoli Federico II, Complesso Universitario di Monte S. Angelo Edificio 6, via Cintia, 80126 Napoli, Italy * Correspondence: [email protected] Received: 14 September 2019; Accepted: 15 October 2019; Published: 19 October 2019 Abstract: In this paper, a generalized form of relativistic dynamics is presented. A realization of the Poincaré algebra is provided in terms of vector fields on the tangent bundle of a simultaneity surface in R4. The construction of this realization is explicitly shown to clarify the role of the commutation relations of the Poincaré algebra versus their description in terms of Poisson brackets in the no-interaction theorem. Moreover, a geometrical analysis of the “eleventh generator” formalism introduced by Sudarshan and Mukunda is outlined, this formalism being at the basis of many proposals which evaded the no-interaction theorem. Keywords: relativistic dynamics; no-interaction theorem; world line condition In memory of E.C.G.
    [Show full text]
  • Lecture 17 Relativity A2020 Prof. Tom Megeath What Are the Major Ideas
    4/1/10 Lecture 17 Relativity What are the major ideas of A2020 Prof. Tom Megeath special relativity? Einstein in 1921 (born 1879 - died 1955) Einstein’s Theories of Relativity Key Ideas of Special Relativity • Special Theory of Relativity (1905) • No material object can travel faster than light – Usual notions of space and time must be • If you observe something moving near light speed: revised for speeds approaching light speed (c) – Its time slows down – Its length contracts in direction of motion – E = mc2 – Its mass increases • Whether or not two events are simultaneous depends on • General Theory of Relativity (1915) your perspective – Expands the ideas of special theory to include a surprising new view of gravity 1 4/1/10 Inertial Reference Frames Galilean Relativity Imagine two spaceships passing. The astronaut on each spaceship thinks that he is stationary and that the other spaceship is moving. http://faraday.physics.utoronto.ca/PVB/Harrison/Flash/ Which one is right? Both. ClassMechanics/Relativity/Relativity.html Each one is an inertial reference frame. Any non-rotating reference frame is an inertial reference frame (space shuttle, space station). Each reference Speed limit sign posted on spacestation. frame is equally valid. How fast is that man moving? In contrast, you can tell if a The Solar System is orbiting our Galaxy at reference frame is rotating. 220 km/s. Do you feel this? Absolute Time Absolutes of Relativity 1. The laws of nature are the same for everyone In the Newtonian universe, time is absolute. Thus, for any two people, reference frames, planets, etc, 2.
    [Show full text]
  • Chapter 2: Minkowski Spacetime
    Chapter 2 Minkowski spacetime 2.1 Events An event is some occurrence which takes place at some instant in time at some particular point in space. Your birth was an event. JFK's assassination was an event. Each downbeat of a butterfly’s wingtip is an event. Every collision between air molecules is an event. Snap your fingers right now | that was an event. The set of all possible events is called spacetime. A point particle, or any stable object of negligible size, will follow some trajectory through spacetime which is called the worldline of the object. The set of all spacetime trajectories of the points comprising an extended object will fill some region of spacetime which is called the worldvolume of the object. 2.2 Reference frames w 1 w 2 w 3 w 4 To label points in space, it is convenient to introduce spatial coordinates so that every point is uniquely associ- ated with some triplet of numbers (x1; x2; x3). Similarly, to label events in spacetime, it is convenient to introduce spacetime coordinates so that every event is uniquely t associated with a set of four numbers. The resulting spacetime coordinate system is called a reference frame . Particularly convenient are inertial reference frames, in which coordinates have the form (t; x1; x2; x3) (where the superscripts here are coordinate labels, not powers). The set of events in which x1, x2, and x3 have arbi- x 1 trary fixed (real) values while t ranges from −∞ to +1 represent the worldline of a particle, or hypothetical ob- x 2 server, which is subject to no external forces and is at Figure 2.1: An inertial reference frame.
    [Show full text]