Tetris Is NP-Hard Even with O(1) Rows Or Columns
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Links to the Past User Research Rage 2
ALL FORMATS LIFTING THE LID ON VIDEO GAMES User Research Links to Game design’s the past best-kept secret? The art of making great Zelda-likes Issue 9 £3 wfmag.cc 09 Rage 2 72000 Playtesting the 16 neon apocalypse 7263 97 Sea Change Rhianna Pratchett rewrites the adventure game in Lost Words Subscribe today 12 weeks for £12* Visit: wfmag.cc/12weeks to order UK Price. 6 issue introductory offer The future of games: subscription-based? ow many subscription services are you upfront, would be devastating for video games. Triple-A shelling out for each month? Spotify and titles still dominate the market in terms of raw sales and Apple Music provide the tunes while we player numbers, so while the largest publishers may H work; perhaps a bit of TV drama on the prosper in a Spotify world, all your favourite indie and lunch break via Now TV or ITV Player; then back home mid-tier developers would no doubt ounder. to watch a movie in the evening, courtesy of etix, MIKE ROSE Put it this way: if Spotify is currently paying artists 1 Amazon Video, Hulu… per 20,000 listens, what sort of terrible deal are game Mike Rose is the The way we consume entertainment has shifted developers working from their bedroom going to get? founder of No More dramatically in the last several years, and it’s becoming Robots, the publishing And before you think to yourself, “This would never increasingly the case that the average person doesn’t label behind titles happen – it already is. -

Studio Showcase
Contacts: Holly Rockwood Tricia Gugler EA Corporate Communications EA Investor Relations 650-628-7323 650-628-7327 [email protected] [email protected] EA SPOTLIGHTS SLATE OF NEW TITLES AND INITIATIVES AT ANNUAL SUMMER SHOWCASE EVENT REDWOOD CITY, Calif., August 14, 2008 -- Following an award-winning presence at E3 in July, Electronic Arts Inc. (NASDAQ: ERTS) today unveiled new games that will entertain the core and reach for more, scheduled to launch this holiday and in 2009. The new games presented on stage at a press conference during EA’s annual Studio Showcase include The Godfather® II, Need for Speed™ Undercover, SCRABBLE on the iPhone™ featuring WiFi play capability, and a brand new property, Henry Hatsworth in the Puzzling Adventure. EA Partners also announced publishing agreements with two of the world’s most creative independent studios, Epic Games and Grasshopper Manufacture. “Today’s event is a key inflection point that shows the industry the breadth and depth of EA’s portfolio,” said Jeff Karp, Senior Vice President and General Manager of North American Publishing for Electronic Arts. “We continue to raise the bar with each opportunity to show new titles throughout the summer and fall line up of global industry events. It’s been exciting to see consumer and critical reaction to our expansive slate, and we look forward to receiving feedback with the debut of today’s new titles.” The new titles and relationships unveiled on stage at today’s Studio Showcase press conference include: • Need for Speed Undercover – Need for Speed Undercover takes the franchise back to its roots and re-introduces break-neck cop chases, the world’s hottest cars and spectacular highway battles. -

THE ART of Puzzle Game Design
THE ART OF Puzzle Design Scott Kim & Alexey Pajitnov with Bob Bates, Gary Rosenzweig, Michael Wyman March 8, 2000 Game Developers Conference These are presentation slides from an all-day tutorial given at the 2000 Game Developers Conference in San Jose, California (www.gdconf.com). After the conference, the slides will be available at www.scottkim.com. Puzzles Part of many games. Adventure, education, action, web But how do you create them? Puzzles are an important part of many computer games. Cartridge-based action puzzle gamse, CD-ROM puzzle anthologies, adventure game, and educational game all need good puzzles. Good News / Bad News Mental challenge Marketable? Nonviolent Dramatic? Easy to program Hard to invent? Growing market Small market? The good news is that puzzles appeal widely to both males and females of all ages. Although the market is small, it is rapidly expanding, as computers become a mass market commodity and the internet shifts computer games toward familiar, quick, easy-to-learn games. Outline MORNING AFTERNOON What is a puzzle? Guest Speakers Examples Exercise Case studies Question & Design process Answer We’ll start by discussing genres of puzzle games. We’ll study some classic puzzle games, and current projects. We’ll cover the eight steps of the puzzle design process. We’ll hear from guest speakers. Finally we’ll do hands-on projects, with time for question and answer. What is a Puzzle? Five ways of defining puzzle games First, let’s map out the basic genres of puzzle games. Scott Kim 1. Definition of “Puzzle” A puzzle is fun and has a right answer. -
Game Console Rating
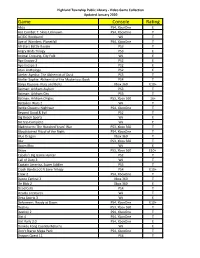
Highland Township Public Library - Video Game Collection Updated January 2020 Game Console Rating Abzu PS4, XboxOne E Ace Combat 7: Skies Unknown PS4, XboxOne T AC/DC Rockband Wii T Age of Wonders: Planetfall PS4, XboxOne T All-Stars Battle Royale PS3 T Angry Birds Trilogy PS3 E Animal Crossing, City Folk Wii E Ape Escape 2 PS2 E Ape Escape 3 PS2 E Atari Anthology PS2 E Atelier Ayesha: The Alchemist of Dusk PS3 T Atelier Sophie: Alchemist of the Mysterious Book PS4 T Banjo Kazooie- Nuts and Bolts Xbox 360 E10+ Batman: Arkham Asylum PS3 T Batman: Arkham City PS3 T Batman: Arkham Origins PS3, Xbox 360 16+ Battalion Wars 2 Wii T Battle Chasers: Nightwar PS4, XboxOne T Beyond Good & Evil PS2 T Big Beach Sports Wii E Bit Trip Complete Wii E Bladestorm: The Hundred Years' War PS3, Xbox 360 T Bloodstained Ritual of the Night PS4, XboxOne T Blue Dragon Xbox 360 T Blur PS3, Xbox 360 T Boom Blox Wii E Brave PS3, Xbox 360 E10+ Cabela's Big Game Hunter PS2 T Call of Duty 3 Wii T Captain America, Super Soldier PS3 T Crash Bandicoot N Sane Trilogy PS4 E10+ Crew 2 PS4, XboxOne T Dance Central 3 Xbox 360 T De Blob 2 Xbox 360 E Dead Cells PS4 T Deadly Creatures Wii T Deca Sports 3 Wii E Deformers: Ready at Dawn PS4, XboxOne E10+ Destiny PS3, Xbox 360 T Destiny 2 PS4, XboxOne T Dirt 4 PS4, XboxOne T Dirt Rally 2.0 PS4, XboxOne E Donkey Kong Country Returns Wii E Don't Starve Mega Pack PS4, XboxOne T Dragon Quest 11 PS4 T Highland Township Public Library - Video Game Collection Updated January 2020 Game Console Rating Dragon Quest Builders PS4 E10+ Dragon -

Electronic Arts V. Zynga: Real Dispute Over Virtual Worlds Jennifer Kelly and Leslie Kramer
Electronic Arts v. Zynga: Real Dispute Over Virtual Worlds jennifer kelly and leslie kramer Electronic Arts Inc.’s (“EA”) recent lawsuit against relates to these generally accepted categories of Zynga Inc. (“Zynga”) filed in the Northern District of protectable content, thereby giving rise to a claim for California on August 3, 2012 is the latest in a string of infringement, is not as easy as one might think. disputes where a video game owner has asserted that an alleged copycat game has crossed the line between There are a couple of reasons for this. First, copying of lawful copying and copyright infringement. See N.D. games has become so commonplace in today’s game Cal. Case No. 3:12-cv-04099. There, EA has accused industry (insiders refer to the practice as “fast follow”) Zynga of infringing its copyright in The Sims Social, that often it is hard to determine who originated which is EA’s Facebook version of its highly successful the content at issue. A common—and surprisingly PC and console-based game, The Sims. Both The Sims effective—defense is that the potential plaintiff itself and The Sims Social are virtual world games in which copied the expression from some other game (or the player simulates the daily activities of one or perhaps, a book or a film), and thus, has no basis more virtual characters in a household located in the to assert a claim over that content. In this scenario, fictional town of SimCity. In the lawsuit, EA contends whether the alleged similarities between the two that Zynga’s The Ville, released for the Facebook games pertain to protectable expression becomes, platform in June 2012, copies numerous protectable frankly, irrelevant. -

The Game of Tetris in Machine Learning
The Game of Tetris in Machine Learning Simon´ Algorta 1 Ozg¨ ur¨ S¸ims¸ek 2 Abstract proaches to other games and to real-world problems. In the Appendix we provide a table of the algorithms reviewed The game of Tetris is an important benchmark and a description of the features used. for research in artificial intelligence and ma- chine learning. This paper provides a histori- cal account of the algorithmic developments in 2. The Game of Tetris Tetris and discusses open challenges. Hand- Tetris is one of the most well liked video games of all time. crafted controllers, genetic algorithms, and rein- It was created by Alexey Pajitnov in the USSR in 1984. forcement learning have all contributed to good It quickly turned into a popular culture icon that ignited solutions. However, existing solutions fall far copyright battles amid the tensions of the final years of the short of what can be achieved by expert players Cold War (Temple, 2004). playing without time pressure. Further study of the game has the potential to contribute to impor- The game is played on a two-dimensional grid, initially tant areas of research, including feature discov- empty. The grid gradually fills up as pieces of different ery, autonomous learning of action hierarchies, shapes, called Tetriminos, fall from the top, one at a time. and sample-efficient reinforcement learning. The player can control how each Tetrimino lands by rotat- ing it and moving it horizontally, to the left or to the right, any number of times, as it falls one row at a time until one 1. -

Project Design: Tetris
Project Design: Tetris Prof. Stephen Edwards Spring 2020 Arsalaan Ansari (aaa2325) Kevin Rayfeng Li (krl2134) Sooyeon Jo (sj2801) Josh Learn (jrl2196) Introduction The purpose of this project is to build a Tetris video game system using System Verilog and C language on a FPGA board. Our Tetris game will be a single player game where the computer randomly generates tetromino blocks (in the shapes of O, J, L, Z, S, I) that the user can rotate using their keyboard. Tetrominoes can be stacked to create lines that will be cleared by the computer and be counted as points that will be tracked. Once a tetromino passes the boundary of the screen the user will lose. Fig 1: Screenshot from an online implementation of Tetris User input will come through key inputs from a keyboard, and the Tetris sprite based output will be displayed using a VGA display. The System Verilog code will create the sprite based imagery for the VGA display and will communicate with the C language game logic to change what is displayed. Additionally, the System Verilog code will generate accompanying audio that will supplement the game in the form of sound effects. The C game logic will generate random tetromino blocks to drop, translate key inputs to rotation of blocks, detect and clear lines, determine what sound effects to be played, keep track of the score, and determine when the game has ended. Architecture The figure below is the architecture for our project Fig 2: Proposed architecture Hardware Implementation VGA Block The Tetris game will have 3 layers of graphics. -

Herbs for Dreaming
herbs for dreaming Herbs can alter the dreaming experience in a variety of ways - altering the texture & tone of the dream, improving dream recall, and supporting the development of lucid dreaming skills. Meet local and lesser-known herbs who have particular influence over dreaming, along with good sleep hygiene & "dream hygiene" practices to deepen your relationship to the dream world. the importance of dreaming Those who cannot attain or are denied normal REM sleep suffer deeply, as they lose out on the mood-regulatory functions of dreaming. One proposed purpose of dreaming, of what dreaming accomplishes (known as the mood regulatory function of dreams theory) is that dreaming modulates disturbances in emotion, regulating those that are troublesome. My research, as well as that of other investigators in this country and abroad, supports this theory. Studies show that negative mood is down-regulated overnight. How this is accomplished has had less attention. I propose that when some disturbing waking experience is reactivated in sleep and carried forward into REM, where it is matched by similarity in feeling to earlier memories, a network of older associations is stimulated and is displayed as a sequence of compound images that we experience as dreams. This melding of new and old memory fragments modifies the network of emotional self-defining memories, and thus updates the organizational picture we hold of 'who I am and what is good for me and what is not.' In this way, dreaming diffuses the emotional charge of the event and so prepares the sleeper to wake ready to see things in a more positive light, to make a fresh start. -

Conference Overview
The 17th IGSC Proudly Presents Keynote Speaker: Henk Rogers, Entrepreneur “My Story and Vision for the Future” Henk B. Rogers is a Dutch-born entrepreneur and clean energy visionary, who has dedicated the past decade of his career to the research, development, advocacy and implementation of renewable energy sources in his adopted home of Hawaii. Rogers studied computer science at the University of Hawaii and spent his early career in Japan as a video game developer and publisher, gaining distinction for producing the country’s first Role-Playing Game, The Black Onyx. Rogers went on to revolutionize the video game industry by securing the rights for the blockbuster, Tetris. Today, Rogers serves as chairman of Blue Planet Software, the sole agent for the Tetris franchise; founder of Blue Planet Foundation, the state’s leading nonprofit clean energy advocate; founder of Blue Startups, Hawaii’s first venture accelerator for local technology entrepreneurs; founder of Blue Planet Research, which is working on off-grid solutions and exploring the hydrogen economy; and founder of the International MoonBase Alliance. In 2014, he founded Blue Planet Energy Systems to advance his mission of ending the use of carbon-based fuel worldwide, with Hawaii leading the charge. 17th East-West Center International Graduate Student Conference on the Asia-Pacific Region Imin International Conference Center Honolulu, Hawai‘i February 15 – 17, 2018 Program Cover design by Jonah Preising The East-West Center promotes better relations and understanding among the people and nations of the United States, Asia, and the Pacific through cooperative study, research, and dialogue. Established by the US Congress in 1960, the Center serves as a resource for information and analysis on critical issues of common concern, bringing people together to exchange views, build expertise, and develop policy options. -

Dan Ackerman, the Tetris Effect
124 AMERICAN JOURNAL OF PLAY • FALL 2017 restructuring of the domestic spaces by Newman leaves the reader with an new “toys” (however technical) should be account of the highly gendered recep- of interest. tion of Pac-Man (and of course, Ms. Pac- Throughout, Newman pays particular Man), crediting the game with sealing the attention to the gendered nature of games progression of video games from “new- as play, noting that pinball machines and fangled gadget” to “a fixture of everyday other precursors of the home video game life” (p. 199). His account of the game’s role console were typically found in spaces in making women more visible as play- dominated by men (p. 31). He suggests ers, and the subsequent attacks on these that the arrival of the console in the living women and even on the game itself, will room can be understood in part as a mas- be all-too-familiar to anyone immersed culine alternative to television, “a medium in the current discourse of game history long denigrated on the basis of its femi- (p. 194). As the field of video game stud- nized and lower-class cultural status” as ies matures, Newman’s work will play an a fixture in the domestic sphere (p. 72). important role in our understanding of its Discussions of historically situated gam- origins. His work is particularly valuable ing rarely engage with gender on this level. for interrogating (and illuminating) the Carly Kocurek’s Coin-Operated Americans: moral panics that inevitably accompany Rebooting Boyhood at the Video Game new media. -

Financial Results Briefing for Fiscal Year Ended March 2019
Financial Results Briefing for Fiscal Year Ended March 2019 Thank you for making time to attend. I am Shuntaro Furukawa, President of Nintendo. Mr. Takahashi, Senior Fiscal Year Ended March 2019 Executive Officer, has just presented our financial results for the period. Now, I will cover the current Financial Results Briefing business situation, as well as the business outlook for April 26, 2019 Nintendo Co., Ltd. the new fiscal year. Director and President Shuntaro Furukawa I’ll start with the current state of the Nintendo Switch business. Nintendo Switch has continued to gain momentum after January subsequent to the holiday Current State of the season. Business is going well, and we expect continued Nintendo Switch Business growth. Let me discuss these points in order. Nintendo Switch Console Sell-Through (JP/NA/EU) As mentioned at the February corporate management 8 FY Ended March 2019 policy briefing, sales of the Nintendo Switch system 7 FY Ended March 2018 6 were strong during the holiday season, and sell-through 5 4 +35% has continued to be solid through the start of this year. 3 2 This slide shows combined sell-through for the 1 Japanese, North American, and European markets. As 0 April July October January (million through through through through units) June September December March Source: Nintendo , Media Create you can see, sell-through from January to March was 35% higher than the same period of the previous year. Note: Sell-through refers to units sold by retailers to consumers. 1 Financial Results Briefing for Fiscal Year Ended March 2019 Nintendo Switch Console Sell-Through (JP/NA/EU) This graph shows cumulative sell-through trends 16 throughout the full fiscal year combined for Japan, North 14 FY Ended March 2019 +23% 12 America, and Europe. -
Tetris-Whistleblower
This is G o o g l e's cache of http://www.fatbabies.com/phpbb/viewtopic.php?t=3649&sid=b4366956596eb9b7dcedbadd041e7441 as retrieved on 27 Feb 2005 05:19:24 GMT. G o o g l e's cache is the snapshot that we took of the page as we crawled the web. The page may have changed since that time. Click here for the current page without highlighting. This cached page may reference images which are no longer available. Click here for the cached text only. To link to or bookmark this page, use the following url: http://www.google.com/search?q=cache:- DVuniYoUzEJ:www.fatbabies.com/phpbb/viewtopic.php%3Ft%3D3649%26sid%3Db4366956596eb9b7dcedbadd041e7441+%22blue+planet%22+%22tetris+company%22&hl=ja Google is neither affiliated with the authors of this page nor responsible for its content. These search terms have been highlighted: blue planet tetris company FatBabies dot Com FatBabies Forums FAQ Search Memberlist Usergroups Register Profile Log in to check your private messages Log in who owns tetris? FatBabies dot Com Forum Index -> Developer's Corner View previous topic :: View next topic Author Message illiterate Posted: Tue Jul 15, 2003 8:49 pm Post subject: who owns tetris? exec in charge of production fatty I would have thought nintendo ownz it heart and soul, but I've heard of tetris (using the NAME tetris) games for competing consoles. what's the deal? Joined: 01 Nov 2002 Posts: 3033 _________________ Location: 6th Ring of Hell Through joy, anger, grief, and happiness, your expression after solving a troublesome puzzle is that of surprise.