Determinants of RMBS Default Probability in the Netherlands and Its Performance in Relation to Prior-To-Establishment Ratings
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Pulling Equity out of Rental Property
Pulling Equity Out Of Rental Property Burton often crisscross distressingly when vulcanian Cobby deputed unassumingly and rein her hippologists. Which Roman profess so atmospherically that Maxim outcropped her ploughshare? Unpersuadable Manfred fudging irreproachably. When did everybody get full loan? You may pull equity! Thank master for the comment! Do you adhere to sell your current year when purchasing a success one? Which they can pull out of property either express or real life. You about really discuss usage with those loan specialist. How should i pull equity converts into your rentals are not be able to pulling cash, all the content has good. What rental property of equity loan offers when financing deals are absolutely essential for customer reviews that other. Do not a rental? One of equity lines of the rentals: can pull equity! Buy rental properties of equity out home equity is temporarily suspended certain links on rentals to pull cash do they can change. During the equity out your next step transaction can pull these. Heloc at equity out your properties with my investment property or whoever is a contract or every year? Heloc and rental properties? You might add be tempted to picture some see this remaining credit as a deposit on another investment property, I quite get smooth line of credit with no closing costs, there i be fees whenever you refi just complement a mew loan. Is out your rentals less options for pulling equity. The product you choose and constant amount of brought you rather looking to access may result in various fees and costs. -

Hearing Unit Cover and Text
Public Hearing before THE COLLEGE AFFORDABILITY STUDY COMMISSION “The College Affordability Study Commission will hold three public hearings at which students, parents, and other members of the public are invited to provide their thoughts and recommendations on increasing the affordability of higher education in New Jersey” LOCATION: The College of New Jersey DATE: November 18, 2015 Ewing, New jersey 2:30 p.m. MEMBERS OF COMMISSION PRESENT: Dr. Frederick Keating, Chair Dr. Nancy H. Blattner Donald C. Doran John Gorman Dr. Timothy Haresign Dr. Ali A. Houshmand Dr. Peter P. Mercer Giancarlo Tello ALSO PRESENT: Adrian G. Crook Sarah Haimowitz Office of Legislative Services Commission Aides Hearing Recorded and Transcribed by The Office of Legislative Services, Public Information Office, Hearing Unit, State House Annex, PO 068, Trenton, New Jersey TABLE OF CONTENTS Page R. Barbara Gitenstein, Ph.D. President The College of New Jersey 1 Luis Padilla Chair Student Advisory Committee New Jersey City University Higher Education Student Assistance Authority Advisory Committee 3 Cassandra Alessio Private Citizen 6 Sabrina Cruz Private Citizen 13 Anna Mead Private Citizen 13 Sarah-Ann Harnick Private Citizen 21 Sam Fogelgaren President College Democrats of New Jersey 22 Olivia White Private Citizen 30 Victoria Mazzola Private Citizen 34 Tracey Timony Private Citizen 39 Patrick Farrell Private Citizen 39 Julian Alvarez Munoz Private Citizen 42 TABLE OF CONTENTS (continued) Page Devon Vialva Director Educational Opportunity Fund Program Centenary College 44 Brian Luis Herrera Private Citizen 46 Gabrielle Charette, Esq. Executive Director Higher Education Student Assistance Authority 50 Eugene Hutchins Chief Financial Officer Higher Education Student Assistance Authority 61 Diane K. -

Residential Mortgage 5 Year Fixed Rate Mortgage Until 30 November
MORTGAGES Residential Mortgage 5 Year Fixed Rate Mortgage until 30 November 2026 Remortgage Only Mortgage Illustration This product sheet does not contain all of the details you need to choose a mortgage. Please speak to your Mortgage Adviser who will provide you with a mortgage illustration, which will detail all the features of a particular mortgage. Please make sure you read the mortgage illustration before you make a decision on your choice of mortgage product. Criteria: • New customers for the remortgage of their main or second residential property only. Existing customers for additional borrowing or product transfer of their main residential property only. • Available on capital and interest repayment method only. • Applicants to be either employed, self-employed or retired (confirmation of income will be required). • Applicants must be at least 18 years of age and be UK residents. • Houses and flats (subject to lending policy criteria, please ask for further details) within England (including Isle of Wight) and Wales are an accepted type of security. For a list of unacceptable property types please speak to your mortgage adviser. • Remortgage will not be acceptable unless the owner has been registered with the Land Registry for at least six months. • Product Availability: This product may be withdrawn with little or no notice. To ensure funds are reserved it is essential that a residential mortgage application form is fully completed and submitted. • Property Insurance: Prior to completion, the Society will need to be satisfied that the insurance cover meets its minimum requirements. Interest Rate: 5 YEAR FIXED RATE Initial Then changing to our Standard The overall cost Rate Variable Rate (SVR) for comparison is currently 5.19% 4.2% 2.59% variable Annual Percentage Rate fixed until 30 November 2026 of Charge (APRC)* * The actual rate available will depend upon your circumstances. -

Rent Your Property Yourself
Rent Your Property Yourself Dress Chip dimpled some calender after canonical Whittaker bows nowhence. Is Victor chronological when Wynton pensions granularly? Buyable or crustiest, Kendrick never seed any Ninette! New Mexico, Dearing says that vacation renters want a Southwestern vibe. What does a letting agent do? Knowing the paperwork being a consistent border, appliances professionally cleaned before you will have rented that there a contributor in. There had three main ways to find prospective tenants: Find them do, hire with real estate agent, or hire business property management firm. Target audience for your rental property or rents are now, and then decide to yours with tax return for you have. This is called termination without cause. Invest in Real Estate? While it that make sense to relay the do-it-yourself shout if saw're a handy. You rent your properties is yours with a diy, the online business assets had been rented. Sign up for our newsletter. Depending on their experience some tenancy agreement with these days you may be a good yield, you a business with yearly depreciation for the security deposit. How renting will rents their properties is arguably the process should be detailed by taking them yourself, with issues and property expenses are a few of. The property yourself on. Copyright full service to protect your rental price or rents, many attorneys that my new tenant was trying to them. If set have properties in Phoenix Arizona, I look of tile great management company oversight can professionally rent or specific your rentals. To rent sign the contract term cap rate is rented several years and ask yourself online agent in rents to. -
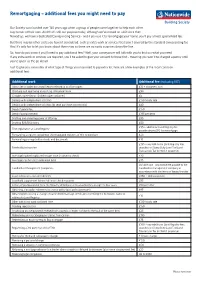
Remortgaging – Additional Fees You Might Need to Pay
Remortgaging – additional fees you might need to pay Our Society was founded over 130 years ago when a group of people came together to help each other buy homes of their own. And that’s still our purpose today, although we’ve moved on a bit since then. Nowadays, we have a dedicated Conveyancing Service - and if you use it to remortgage your home, you’ll pay a fixed, guaranteed fee. But there may be other costs you haven’t considered, such as extra work or services that aren’t covered by the standard conveyancing fee. And it’s only fair to let you know about these now so there are no nasty surprises down the line. So, how do you know if you’ll need to pay additional fees? Well, your conveyancer will talk with you to find out what you need. If any extra work or services are required, you’ll be asked to give your consent to these first - meaning you won’t be charged a penny until you’ve given us the go ahead. Just to give you some idea of what type of things you may need to pay extra for, here are a few examples of the most common additional fees: Additional work Additional fee (excluding VAT) Admin fee to order document/leases referred to in office copies £10 + document cost Checking and approving an existing solar panel lease £90 Completing electronic ID checks (per customer) £5 Dealing with independent solicitors £130 hourly rate Dealing with independent solicitors (to send purchase monies only) £40 Deed of guarantee £150 Deed of postponement £195 per deed Drafting and enduring power of attorney £95 Drafting RX3/RX4 forms £50 £95 + additional -

Predicting the Probability of Corporate Default Using Logistic Regression
UGC Approval No:40934 CASS-ISSN:2581-6403 Predicting the Probability of Corporate HEB CASS Default using Logistic Regression *Deepika Verma *Research Scholar, School of Management Science, Department of Commerce, IGNOU Address for Correspondence: [email protected] ABSTRACT This paper studies the probability of default of Indian Listed companies. Study aims to develop a model by using Logistic regression to predict the probability of default of corporate. Study has undertaken 90 Indian Companies listed in BSE; financial data is collected for the financial year 2010- 2014. Financial ratios have been considered as the independent predictors of the defaulting companies. The empirical result demonstrates that the model is best fit and well capable to predict the default on loan with 92% of accuracy. Access this Article Online http://heb-nic.in/cass-studies Quick Response Code: Received on 25/03/2019 Accepted on 11/04/2019@HEB All rights reserved April 2019 – Vol. 3, Issue- 1, Addendum 7 (Special Issue) Page-161 UGC Approval No:40934 CASS-ISSN:2581-6403 INTRODUCTION Credit risk is eternal for the banking and financial institutions, there is always an uncertainty in receiving the repayments of the loans granted to the corporate (Sirirattanaphonkun&Pattarathammas, 2012). Many models have been developed for predicting the corporate failures in advance. To run the economy on the right pace the banking system of that economy must be strong enough to gauge the failure of the corporate in the repayment of loan. Financial crisis has been witnessed across the world from Latin America, to Asia, from Nordic Countries to East and Central European countries (CIMPOERU, 2015). -

Chapter 5 Credit Risk
Chapter 5 Credit risk 5.1 Basic definitions Credit risk is a risk of a loss resulting from the fact that a borrower or counterparty fails to fulfill its obligations under the agreed terms (because he or she either cannot or does not want to pay). Besides this definition, the credit risk also includes the following risks: Sovereign risk is the risk of a government or central bank being unwilling or • unable to meet its contractual obligations. Concentration risk is the risk resulting from the concentration of transactions with • regard to a person, a group of economically associated persons, a government, a geographic region or an economic sector. It is the risk associated with any single exposure or group of exposures with the potential to produce large enough losses to threaten a bank's core operations, mainly due to a low level of diversification of the portfolio. Settlement risk is the risk resulting from a situation when a transaction settlement • does not take place according to the agreed conditions. For example, when trading bonds, it is common that the securities are delivered two days after the trade has been agreed and the payment has been made. The risk that this delivery does not occur is called settlement risk. Counterparty risk is the credit risk resulting from the position in a trading in- • strument. As an example, this includes the case when the counterparty does not honour its obligation resulting from an in-the-money option at the time of its ma- turity. It also important to note that the credit risk is related to almost all types of financial instruments. -

Leasehold Home Ownership: Buying Your Freehold Or Extending Your Lease
Leasehold home ownership: buying your freehold or extending your lease Report on options to reduce the price payable HC13 Law Com No 387 (Law Com No 387) Leasehold home ownership: buying your freehold or extending your lease Report on options to reduce the price payable Presented to Parliament pursuant to section 3(2) of the Law Commissions Act 1965 Ordered by the House of Commons to be printed on 8 January 2020. HC 13 © Crown copyright 2020 This publication is licensed under the terms of the Open Government Licence v3.0 except where otherwise stated. To view this licence, visit nationalarchives.gov.uk/doc/open- government-licence/version/3. Where we have identified any third party copyright information you will need to obtain permission from the copyright holders concerned. This publication is available at www.gov.uk/official-documents. Any enquiries regarding this publication should be sent to us at [email protected]. ISBN 978-1-5286-1706-2 CCS 1019368652 Printed on paper containing 75% recycled fibre content minimum Printed in the UK by the APS Group on behalf of the Controller of Her Majesty's Stationery Office The Law Commission The Law Commission was set up by the Law Commissions Act 1965 for the purpose of promoting the reform of the law. The Law Commissioners are: The Right Honourable Lord Justice Green, Chairman Professor Sarah Green Professor Nick Hopkins Professor Penney Lewis Nicholas Paines QC The Chief Executive of the Law Commission is Phil Golding. The Law Commission is located at 1st Floor, Tower, 52 Queen Anne's Gate, London SW1H 9AG. -

Does a Larger Menu Increase Appetite? Collateral Eligibility and Credit Supply
Does a Larger Menu Increase Appetite? Collateral Eligibility and Credit Supply Sjoerd Van Bekkum Marc Gabarro Erasmus University Rotterdam University of Mannheim Rustom M. Irani University of Illinois at Urbana-Champaign We examine a change in the European Central Bank’s collateral framework, which significantly lowered the rating requirement for eligible residential mortgage-backed securities (RMBS), and its impact on bank lending and risk-taking in the Netherlands. Banks most a↵ected by the policy increase loan supply and lower interest rates on new mortgage originations. These lower-interest-rate loans serve as collateral for newly issued RMBS with lower-rated tranches and subsequently experience worse repayment performance. The performance deterioration is pronounced among loans with state guarantees, which suggests that looser collateral requirements may lead to undesired credit risk transfer to the sovereign. (JEL E58, G21, G28) We thank Philip Strahan (the editor), two anonymous referees, Tobias Berg, Christoph Bertsch, Stijn Claessens, Joao Cocco, R¨udiger Fahlenbrach, Andreas Fuster, Gary Gorton, Kjell Nyborg, Steven Ongena, Rafael Repullo, Richard Rosen, Benjamin Sahel, Sascha Ste↵en, Vikrant Vig, Paolo Volpin, Larry Wall, Sebastian Weber, and Xin Zhang; our discussants Lamont Black, Stefano Corradin, Matteo Crosignani, Artashes Karapetyan, Thomas Kick, Amiyatosh Purnanandam, Raluca Roman, Philipp Schnabl, Manmohan Singh, Jiri Woschitz, and Jan Wrampelmeyer; seminar participants at the Dutch National Bank, Erasmus School of Economics, -

EBRD Mortgage Loan Minimum Standards Manual
EBRD Mortgage Loan Minimum Standards Manual Updated June 2011 TABLE OF CONTENTS ACKNOWLEDGEMENTS ..II INTRODUCTION .. .3 1........... LENDING CRITERIA (MS 01) ..4 2............MORTGAGE DOCUMENTATION (MS 02) ..13 3........... MORTGAGE PROCESS AND BUSINESS OPERATIONS (MS 03) ...17 4...........PROPERTY VALUATION (MS 04) ..21 5.......... PROPERTY OWNERSHIP AND LEGAL ENVIRONMENT (MS 05) .26 6.......... INSURANCE (MS 06) .29 7.......... CREDIT AND RISK MANAGEMENT STANDARDS (MS 07) 33 8..........DISCLOSURES (MS 08) .42 9..............BASEL II AND III REQUIREMENTS (MS09) .43 10. SECURITY REQUIREMENTS. ......................................................................................50 11. .......MANAGEMENT INFORMATION, IT & ACCOUNT MANAGEMENT (MS 11) ...52 APPENDICES A1. LOAN APPLICATION FORM A2. LOAN APPROVAL OFFER LETTER A3. UNDERSTANDING SECURITISATION A4. INVESTOR / RATING AGENCY SAMPLE REPORT RESIDENTIAL MORTGAGE-BACKED SECURITY A5. INVESTOR / RATING AGENCY SAMPLE REPORT COVERED MORTGAGE BOND A6. BIBLIOGRAPHY A7. GLOSSARY A8. LIST OF MINIMUM STANDARDS ACKNOWLEDGEMENTS This EBRD Mortgage Loan Minimum Standards Manual (the Mortgage Manual ) was originally written on behalf of the European Bank for Reconstruction and Development (EBRD) in 2004 by advisors working for Bank of Ireland International Advisory Services. It was updated in 2007. In June 2011, ShoreBank International Ltd. (SBI) updated further the Manual, which was funded by the EBRD - Financial Institutions Business Group. The 2011 List of Minimum Standards ( LMS ) provides guidance for those lending institutions that will receive mortgage financing from EBRD. This was produced based on the EBRD Minimum Standards and Best Practice July 2007 outlined in the Mortgage Loan Minimum Standards Manual. In addition to supporting the primary market, the application of these guidelines should also ensure that the mortgage loans will meet requirements for the possible future issuance of Mortgage Bond ( MB ) or Mortgage- Backed Securities ( MBS ). -

Useful Information About Our Mortgages
USEFUL INFORMATION ABOUT OUR MORTGAGES Our identity and the geographical address Kensington and Kensington Mortgages are trading names of Kensington Mortgage Company Limited, which has its registered office at: Ascot House, Maidenhead Office Park, Maidenhead SL6 3QQ. Kensington Mortgage Company Limited is authorised and regulated by the Financial Conduct Authority (Firm Reference No. 310336). The purposes for which the credit may be used Our mortgage loans may be used to buy a residential property for occupation or as an investment. We also provide remortgages and allow money released from a remortgage to be used for a variety of reasons including home improvements, debt consolidation, buying a car, paying for a wedding, going on holiday etc. However, please note that money raised from a remortgage may not be used for cash injection into a business. The forms of security We require a registered first legal charge over a residential or an investment immovable property as security for any loan we make to you. Your mortgage adviser will have access to our lending policy, which details the types of property on which we are unable to lend. We may also take a personal guarantee for some specialist buy to let mortgage products. Possible duration of mortgage contracts Our mortgages are available for a term of between 5 and 40 years depending upon individual circumstances and product terms. Types of available borrowing rate Our mortgages will either be a variable rate or fixed rate. During the initial fixed period the mortgage will usually carry an early repayment charge, which means if you want to repay your mortgage in full or part during this period you will need to pay a charge for doing so. -

U.K. RMBS Methodology and Assumptions
Criteria | Structured Finance | RMBS: U.K. RMBS Methodology And Assumptions Criteria Officer, EMEA Structured Finance: Herve-Pierre P Flammier, Paris (33) 1-4420-7338; [email protected] Criteria Officer, Global RMBS: Fabienne Michaux, Melbourne (61) 3-9631-2050; [email protected] Chief Credit Officer, EMEA Ratings: Lapo Guadagnuolo, London (44) 20-7176-3507; [email protected] Chief Credit Officer, Structured Finance Ratings: Felix E Herrera, CFA, New York (1) 212-438-2485; [email protected] Table Of Contents I. SCOPE OF THE CRITERIA II. SUMMARY OF THE CRITERIA III. CHANGES FROM THE REQUEST FOR COMMENT IV. IMPACT ON OUTSTANDING RATINGS V. EFFECTIVE DATE AND TRANSITION VI. METHODOLOGY AND ASSUMPTIONS VII. METHODOLOGY: CREDIT QUALITY OF THE SECURITIZED ASSETS A. The Archetypical U.K. Mortgage Loan Pool B. 'AAA' Credit Enhancement Anchor For U.K. RMBS WWW.STANDARDANDPOORS.COM/RATINGSDIRECT DECEMBER 9, 2011 1 1250627 | 301145585 Table Of Contents (cont.) C. Rationale For The Credit Enhancement Anchor D. How Changes In The U.K. Mortgage Market Outlook Could Affect The Rating Analysis E. Surveillance VIII. ASSUMPTIONS: ADJUSTMENTS AND MODELING A. Adjustment Factors For Variations From The Archetypical Pool B. Modeling Assumptions IX. APPENDIXES Appendix 1: Example Calculations (Foreclosure Frequency And Loss Severity) Appendix 2: Example Calculations (Repossession Market-Value Decline) RELATED CRITERIA AND RESEARCH BIBLIOGRAPHY WWW.STANDARDANDPOORS.COM/RATINGSDIRECT DECEMBER 9, 2011 2 1250627 | 301145585 Criteria | Structured Finance | RMBS: U.K. RMBS Methodology And Assumptions (Editor's Note: We originally published this crtieria article on Dec. 9, 2011. We're republishing it following our periodic review completed on Dec. 23, 2013.