Introduction to Gauss
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Sagemath and Sagemathcloud
Viviane Pons Ma^ıtrede conf´erence,Universit´eParis-Sud Orsay [email protected] { @PyViv SageMath and SageMathCloud Introduction SageMath SageMath is a free open source mathematics software I Created in 2005 by William Stein. I http://www.sagemath.org/ I Mission: Creating a viable free open source alternative to Magma, Maple, Mathematica and Matlab. Viviane Pons (U-PSud) SageMath and SageMathCloud October 19, 2016 2 / 7 SageMath Source and language I the main language of Sage is python (but there are many other source languages: cython, C, C++, fortran) I the source is distributed under the GPL licence. Viviane Pons (U-PSud) SageMath and SageMathCloud October 19, 2016 3 / 7 SageMath Sage and libraries One of the original purpose of Sage was to put together the many existent open source mathematics software programs: Atlas, GAP, GMP, Linbox, Maxima, MPFR, PARI/GP, NetworkX, NTL, Numpy/Scipy, Singular, Symmetrica,... Sage is all-inclusive: it installs all those libraries and gives you a common python-based interface to work on them. On top of it is the python / cython Sage library it-self. Viviane Pons (U-PSud) SageMath and SageMathCloud October 19, 2016 4 / 7 SageMath Sage and libraries I You can use a library explicitly: sage: n = gap(20062006) sage: type(n) <c l a s s 'sage. interfaces .gap.GapElement'> sage: n.Factors() [ 2, 17, 59, 73, 137 ] I But also, many of Sage computation are done through those libraries without necessarily telling you: sage: G = PermutationGroup([[(1,2,3),(4,5)],[(3,4)]]) sage : G . g a p () Group( [ (3,4), (1,2,3)(4,5) ] ) Viviane Pons (U-PSud) SageMath and SageMathCloud October 19, 2016 5 / 7 SageMath Development model Development model I Sage is developed by researchers for researchers: the original philosophy is to develop what you need for your research and share it with the community. -

WEEK 10: FAREWELL to PYTHON... WELCOME to MAPLE! 1. a Review of PYTHON's Features During the Past Few Weeks, We Have Explored
WEEK 10: FAREWELL TO PYTHON... WELCOME TO MAPLE! 1. A review of PYTHON’s features During the past few weeks, we have explored the following aspects of PYTHON: • Built-in types: integer, long integer, float, complex, boolean, list, se- quence, string etc. • Operations on built-in types: +, −, ∗, abs, len, append, etc. • Loops: N = 1000 i=1 q = [] while i <= N q.append(i*i) i += 1 • Conditional statements: if x < y: min = x else: min = y • Functions: def fac(n): if n==0 then: return 1 else: return n*fac(n-1) • Modules: math, turtle, etc. • Classes: Rational, Vector, Polynomial, Polygon, etc. With these features, PYTHON is a powerful tool for doing mathematics on a computer. In particular, the use of modules makes it straightforward to add greater functionality, e.g. GL (3D graphics), NumPy (numerical algorithms). 2. What about MAPLE? MAPLE is really designed to be an interactive tool. Nevertheless, it can also be used as a programming language. It has some of the basic facilities available in PYTHON: Loops; conditional statements; functions (in the form of “procedures”); good graphics and some very useful additional modules called “packages”: • Built-in types: long integer, float (arbitrary precision), complex, rational, boolean, array, sequence, string etc. • Operations on built-in types: +, −, ∗, mathematical functions, etc. • Loops: 1 2 WEEK 10: FAREWELL TO PYTHON... WELCOME TO MAPLE! Table 1. Some of the most useful MAPLE packages Name Description Example DEtools Tools for differential equations exactsol(ode,y) linalg Linear Algebra gausselim(A) plots Graphics package polygonplot(p,axes=none) stats Statistics package random[uniform](10) N := 1000 : q := array(1..N) : for i from 1 to N do q[i] := i*i : od : • Conditional statements: if x < y then min := x else min := y fi: • Functions: fac := proc(n) if n=0 then return 1 else return n*fac(n-1) fi : end proc : • Packages: See Table 1. -

Practical Estimation of High Dimensional Stochastic Differential Mixed-Effects Models
Practical Estimation of High Dimensional Stochastic Differential Mixed-Effects Models Umberto Picchinia,b,∗, Susanne Ditlevsenb aDepartment of Mathematical Sciences, University of Durham, South Road, DH1 3LE Durham, England. Phone: +44 (0)191 334 4164; Fax: +44 (0)191 334 3051 bDepartment of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen, Denmark Abstract Stochastic differential equations (SDEs) are established tools to model physical phenomena whose dynamics are affected by random noise. By estimating parameters of an SDE intrin- sic randomness of a system around its drift can be identified and separated from the drift itself. When it is of interest to model dynamics within a given population, i.e. to model simultaneously the performance of several experiments or subjects, mixed-effects mod- elling allows for the distinction of between and within experiment variability. A framework to model dynamics within a population using SDEs is proposed, representing simultane- ously several sources of variation: variability between experiments using a mixed-effects approach and stochasticity in the individual dynamics using SDEs. These stochastic differ- ential mixed-effects models have applications in e.g. pharmacokinetics/pharmacodynamics and biomedical modelling. A parameter estimation method is proposed and computational guidelines for an efficient implementation are given. Finally the method is evaluated using simulations from standard models like the two-dimensional Ornstein-Uhlenbeck (OU) and the square root models. Keywords: automatic differentiation, closed-form transition density expansion, maximum likelihood estimation, population estimation, stochastic differential equation, Cox-Ingersoll-Ross process arXiv:1004.3871v2 [stat.CO] 3 Oct 2010 1. INTRODUCTION Models defined through stochastic differential equations (SDEs) allow for the represen- tation of random variability in dynamical systems. -

Towards a Fully Automated Extraction and Interpretation of Tabular Data Using Machine Learning
UPTEC F 19050 Examensarbete 30 hp August 2019 Towards a fully automated extraction and interpretation of tabular data using machine learning Per Hedbrant Per Hedbrant Master Thesis in Engineering Physics Department of Engineering Sciences Uppsala University Sweden Abstract Towards a fully automated extraction and interpretation of tabular data using machine learning Per Hedbrant Teknisk- naturvetenskaplig fakultet UTH-enheten Motivation A challenge for researchers at CBCS is the ability to efficiently manage the Besöksadress: different data formats that frequently are changed. Significant amount of time is Ångströmlaboratoriet Lägerhyddsvägen 1 spent on manual pre-processing, converting from one format to another. There are Hus 4, Plan 0 currently no solutions that uses pattern recognition to locate and automatically recognise data structures in a spreadsheet. Postadress: Box 536 751 21 Uppsala Problem Definition The desired solution is to build a self-learning Software as-a-Service (SaaS) for Telefon: automated recognition and loading of data stored in arbitrary formats. The aim of 018 – 471 30 03 this study is three-folded: A) Investigate if unsupervised machine learning Telefax: methods can be used to label different types of cells in spreadsheets. B) 018 – 471 30 00 Investigate if a hypothesis-generating algorithm can be used to label different types of cells in spreadsheets. C) Advise on choices of architecture and Hemsida: technologies for the SaaS solution. http://www.teknat.uu.se/student Method A pre-processing framework is built that can read and pre-process any type of spreadsheet into a feature matrix. Different datasets are read and clustered. An investigation on the usefulness of reducing the dimensionality is also done. -

An Introduction to Maple
A little bit of help with Maple School of Mathematics and Applied Statistics University of Wollongong 2008 A little bit of help with Maple Welcome! The aim of this manual is to provide you with a little bit of help with Maple. Inside you will find brief descriptions on a lot of useful commands and packages that are commonly needed when using Maple. Full worked examples are presented to show you how to use the Maple commands, with different options given, where the aim is to teach you Maple by example – not by showing the full technical detail. If you want the full detail, you are encouraged to look at the Maple Help menu. To use this manual, a basic understanding of mathematics and how to use a computer is assumed. While this manual is based on Version 10.01 of Maple on the PC platform on Win- dows XP, most of it should be applicable to other versions, platforms and operating systems. This handbook is built upon the original version of this handbook by Maureen Edwards and Alex Antic. Further information has been gained from the Help menu in Maple itself. If you have any suggestions or comments, please email them to Grant Cox ([email protected]). Table of contents : Index 1/81 Contents 1 Introduction 4 1.1 What is Maple? ................................... 4 1.2 Getting started ................................... 4 1.3 Operators ...................................... 7 1.3.1 The Ditto Operator ............................. 9 1.4 Assign and unassign ................................ 9 1.5 Special constants .................................. 11 1.6 Evaluation ...................................... 11 1.6.1 Digits ................................... -

Sage Tutorial (Pdf)
Sage Tutorial Release 9.4 The Sage Development Team Aug 24, 2021 CONTENTS 1 Introduction 3 1.1 Installation................................................4 1.2 Ways to Use Sage.............................................4 1.3 Longterm Goals for Sage.........................................5 2 A Guided Tour 7 2.1 Assignment, Equality, and Arithmetic..................................7 2.2 Getting Help...............................................9 2.3 Functions, Indentation, and Counting.................................. 10 2.4 Basic Algebra and Calculus....................................... 14 2.5 Plotting.................................................. 20 2.6 Some Common Issues with Functions.................................. 23 2.7 Basic Rings................................................ 26 2.8 Linear Algebra.............................................. 28 2.9 Polynomials............................................... 32 2.10 Parents, Conversion and Coercion.................................... 36 2.11 Finite Groups, Abelian Groups...................................... 42 2.12 Number Theory............................................. 43 2.13 Some More Advanced Mathematics................................... 46 3 The Interactive Shell 55 3.1 Your Sage Session............................................ 55 3.2 Logging Input and Output........................................ 57 3.3 Paste Ignores Prompts.......................................... 58 3.4 Timing Commands............................................ 58 3.5 Other IPython -

How Maple Compares to Mathematica
How Maple™ Compares to Mathematica® A Cybernet Group Company How Maple™ Compares to Mathematica® Choosing between Maple™ and Mathematica® ? On the surface, they appear to be very similar products. However, in the pages that follow you’ll see numerous technical comparisons that show that Maple is much easier to use, has superior symbolic technology, and gives you better performance. These product differences are very important, but perhaps just as important are the differences between companies. At Maplesoft™, we believe that given great tools, people can do great things. We see it as our job to give you the best tools possible, by maintaining relationships with the research community, hiring talented people, leveraging the best available technology even if we didn’t write it ourselves, and listening to our customers. Here are some key differences to keep in mind: • Maplesoft has a philosophy of openness and community which permeates everything we do. Unlike Mathematica, Maple’s mathematical engine has always been developed by both talented company employees and by experts in research labs around the world. This collaborative approach allows Maplesoft to offer cutting-edge mathematical algorithms solidly integrated into the most natural user interface available. This openness is also apparent in many other ways, such as an eagerness to form partnerships with other organizations, an adherence to international standards, connectivity to other software tools, and the visibility of the vast majority of Maple’s source code. • Maplesoft offers a solution for all your academic needs, including advanced tools for mathematics, engineering modeling, distance learning, and testing and assessment. By contrast, Wolfram Research has nothing to offer for automated testing and assessment, an area of vital importance to academic life. -

Go Figure with PTC Mathcad 14.0
36 Design Product News dpncanada.com June/July 2007 Technical Literature CAD Industry Watch Ethernet-compatible ac drive. Baldor has published a 28-page guide to an Ethernet- compatible 3-phase ac drive series for higher Maple 11 math software really adds up power machinery applications. The catalog details the drive’s architecture and introduces the Ethernet Powerlink protocol. By Bill Fane (“New command for baldormotion.com/br1202 Info Card 420 computing hypergeo- metric solutions of a Rapid prototyping. Brochure describes ecause of the limitations of spread- linear difference equa- Dimension 3D printers distributed by BRT sheet programs, software developers tion with hypergeo- Solutions that generate working models B have come up with programs aimed metric coefficients”), from CAD files in ABS plastic. Colors avail- specifically at the mathematical computa- so here are some of the able are white, red, blue, green, gray, yellow tion market. One of the early leaders in this high spots. and red. arena was Maplesoft, and over the years The three main areas brt-solutions.com Info Card 421 they have continued to develop their Maple of interest in Maple 11 product to maintain its position on the lead- are the document inter- Antennas, transformers. Pulse, a Technitrol ing edge. face, the computation Company, has announced the Pulse 2007 engine, and its connec- Product Catalog. The catalog features anten- NASA might have tivity capabilities. nas for consumer and automotive applica- Let’s start with the tions, automotive coils and transformers, plus avoided the Mars interface. The interest- unfiltered connectors for networking and tele- ing one here is self- Maple software can transform dynamic equations communications infrastructure and consumer probe disaster documenting context menus. -

Reversible Thinking Ability in Calculus Learn-Ing Using Maple Software: a Case Study of Mathematics Education Students
International Journal of Recent Technology and Engineering (IJRTE) ISSN: 2277-3878,Volume-8, Issue- 1C2, May 2019 Reversible Thinking Ability in Calculus Learn-ing using Maple Software: A Case Study of Mathematics Education Students Lalu Saparwadi, Cholis Sa’dijah, Abdur Rahman As’ari, Tjang Daniel Chandra Abstract: Along with the rapid advancement of technology, the it is done manually. To overcome this, we need a technology lecturers are demanded to be able to integrate technological tool that can facilitate and help students without manual developments in the teaching process. Calculus as a subject calculations that are sometimes less accurate. One of the matter in mathematics education study program which is full of learning technologies that can be utilized is maple software algebraic symbols and graph simulation requires visualization media. Maple software is one of the most appropriate technology [3]. Maple is software that can be used not only as a tools which can be used in teaching Calculus for mathematics calculating tool but also as a tool for creating graphics, education students. The linkage of graphic visualization of determining the derivative of a function and so on. derivative and anti-derivative functions can be understood The use of learning technologies, such as Maple, is only a through reversible thinking. Thus, this study aimed at identifying supporting tool for students to show the results obtained students’ reversible thinking abilities of mathematics education from manual calculation. The results obtained from manual study programs Calculus learning by using Maple. The research design used was a case study. The results of this study indicate calculation can be reviewed based on the results obtained that reversible thinking abilities can be identified when students from the Maple software [4]. -

Insight MFR By
Manufacturers, Publishers and Suppliers by Product Category 11/6/2017 10/100 Hubs & Switches ASCEND COMMUNICATIONS CIS SECURE COMPUTING INC DIGIUM GEAR HEAD 1 TRIPPLITE ASUS Cisco Press D‐LINK SYSTEMS GEFEN 1VISION SOFTWARE ATEN TECHNOLOGY CISCO SYSTEMS DUALCOMM TECHNOLOGY, INC. GEIST 3COM ATLAS SOUND CLEAR CUBE DYCONN GEOVISION INC. 4XEM CORP. ATLONA CLEARSOUNDS DYNEX PRODUCTS GIGAFAST 8E6 TECHNOLOGIES ATTO TECHNOLOGY CNET TECHNOLOGY EATON GIGAMON SYSTEMS LLC AAXEON TECHNOLOGIES LLC. AUDIOCODES, INC. CODE GREEN NETWORKS E‐CORPORATEGIFTS.COM, INC. GLOBAL MARKETING ACCELL AUDIOVOX CODI INC EDGECORE GOLDENRAM ACCELLION AVAYA COMMAND COMMUNICATIONS EDITSHARE LLC GREAT BAY SOFTWARE INC. ACER AMERICA AVENVIEW CORP COMMUNICATION DEVICES INC. EMC GRIFFIN TECHNOLOGY ACTI CORPORATION AVOCENT COMNET ENDACE USA H3C Technology ADAPTEC AVOCENT‐EMERSON COMPELLENT ENGENIUS HALL RESEARCH ADC KENTROX AVTECH CORPORATION COMPREHENSIVE CABLE ENTERASYS NETWORKS HAVIS SHIELD ADC TELECOMMUNICATIONS AXIOM MEMORY COMPU‐CALL, INC EPIPHAN SYSTEMS HAWKING TECHNOLOGY ADDERTECHNOLOGY AXIS COMMUNICATIONS COMPUTER LAB EQUINOX SYSTEMS HERITAGE TRAVELWARE ADD‐ON COMPUTER PERIPHERALS AZIO CORPORATION COMPUTERLINKS ETHERNET DIRECT HEWLETT PACKARD ENTERPRISE ADDON STORE B & B ELECTRONICS COMTROL ETHERWAN HIKVISION DIGITAL TECHNOLOGY CO. LT ADESSO BELDEN CONNECTGEAR EVANS CONSOLES HITACHI ADTRAN BELKIN COMPONENTS CONNECTPRO EVGA.COM HITACHI DATA SYSTEMS ADVANTECH AUTOMATION CORP. BIDUL & CO CONSTANT TECHNOLOGIES INC Exablaze HOO TOO INC AEROHIVE NETWORKS BLACK BOX COOL GEAR EXACQ TECHNOLOGIES INC HP AJA VIDEO SYSTEMS BLACKMAGIC DESIGN USA CP TECHNOLOGIES EXFO INC HP INC ALCATEL BLADE NETWORK TECHNOLOGIES CPS EXTREME NETWORKS HUAWEI ALCATEL LUCENT BLONDER TONGUE LABORATORIES CREATIVE LABS EXTRON HUAWEI SYMANTEC TECHNOLOGIES ALLIED TELESIS BLUE COAT SYSTEMS CRESTRON ELECTRONICS F5 NETWORKS IBM ALLOY COMPUTER PRODUCTS LLC BOSCH SECURITY CTC UNION TECHNOLOGIES CO FELLOWES ICOMTECH INC ALTINEX, INC. -
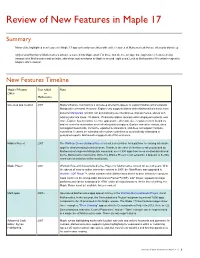
Review of New Features in Maple 17
Review of New Features in Maple 17 Summary Many of the highlighted new features in Maple 17 appear heavily correlated with earlier features of Mathematica® but are often only skin-deep. Only a small fraction of Mathematica’s advances make it into Maple at all. For those that do, the average time lag between features being introduced in Mathematica and an initial, skin-deep implementation in Maple is around eight years. Look at Mathematica 9 for what to expect in Maple’s 2021 release! New Features Timeline Maple 17 Feature Year Added Notes 2013 to Mathematica H L One-step app creation 2007 Maple's Explore command is a skin-deep attempt to appear to support Mathematica's popular Manipulate command. However, Explore only supports sliders while Mathematica's much more powerful Manipulate function can automatically use checkboxes, pop-up menus, sliders with arbitrary discrete steps, 2D sliders, 2D discrete sliders, locators within displayed contents, and more. Explore has no control over the appearance, direction, size, or placement of its sliders and no control or automation over refresh quality or triggers. Explore cannot be nested, does not support bookmarks, cannot be exported to animations, and does not support hardware controllers. It cannot be extended with custom controllers or automatically embedded in generated reports. Mathematica supports all of this and more. Möbius Project 2007 The Wolfram Demonstrations Project set out a clear vision for a platform for sharing interactive apps for demonstrating technical ideas. Thanks to the ease of interface creation provided by Mathematica's superior Manipulate command, over 8,500 apps have been created and shared by the Mathematica community. -

Maple 7 Programming Guide
Maple 7 Programming Guide M. B. Monagan K. O. Geddes K. M. Heal G. Labahn S. M. Vorkoetter J. McCarron P. DeMarco c 2001 by Waterloo Maple Inc. ii • Waterloo Maple Inc. 57 Erb Street West Waterloo, ON N2L 6C2 Canada Maple and Maple V are registered trademarks of Waterloo Maple Inc. c 2001, 2000, 1998, 1996 by Waterloo Maple Inc. All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the copyright holder, except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use of general descriptive names, trade names, trademarks, etc., in this publication, even if the former are not especially identified, is not to be taken as a sign that such names, as understood by the Trade Marks and Merchandise Marks Act, may accordingly be used freely by anyone. Contents 1 Introduction 1 1.1 Getting Started ........................ 2 Locals and Globals ...................... 7 Inputs, Parameters, Arguments ............... 8 1.2 Basic Programming Constructs ............... 11 The Assignment Statement ................. 11 The for Loop......................... 13 The Conditional Statement ................. 15 The while Loop....................... 19 Modularization ........................ 20 Recursive Procedures ..................... 22 Exercise ............................ 24 1.3 Basic Data Structures .................... 25 Exercise ............................ 26 Exercise ............................ 28 A MEMBER Procedure ..................... 28 Exercise ............................ 29 Binary Search ......................... 29 Exercises ........................... 30 Plotting the Roots of a Polynomial ............. 31 1.4 Computing with Formulæ .................. 33 The Height of a Polynomial ................. 34 Exercise ...........................