Prediction of Pakistan Super League-2020 Using TOPSIS and Fuzzy TOPSIS Methods
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Beyond Boundaries II
Beyond Boundaries II Beyond Boundaries II Pakistan - Afghanistan Track 1.5 and II cc Connecting People Building Peace Promoting Cooperation 1 Beyond Boundaries II Beyond Boundaries II Pakistan – Afghanistan Track 1.5 and II Connecting People Building Peace Promoting Cooperation 2 Beyond Boundaries II Beyond Boundaries II ©Center for Research and Security Studies 2018 All rights reserved This publication can be ordered from CRSS Islamabad office. All CRSS publications are also available free of cost for digital download from the CRSS website. 14-M, Ali Plaza, 2nd Floor, F-8 Markaz, Islamabad, Pakistan. Tel: +92-51-8314801-03 Fax: +92-51-8314804 www.crss.pk 3 Beyond Boundaries II TABLE OF CONTENTS 1. ACRONYMS ..................................................................................................... 5 2. EXECUTIVE SUMMARY .................................................................................... 9 3. CONTEXTUALIZING BEYOND BOUNDARIES................................................... 11 4. FIRST MEETING OF THE PAKISTAN AFGHANISTAN JOINT COMMITTEE ........ 56 5. SECOND MEETING OF PAKISTAN AFGHANISTAN JOINT COMMITTEE .......... 72 6. THIRD MEETING OF PAKISTAN AFGHANISTAN JOINT COMMITTEE .............. 95 7. FOURTH MEETING OF PAKISTAN AFGHANISTAN JOINT COMMITTEE ........ 126 8. FIFTH MEETING OF PAKISTAN AFGHANISTAN JOINT COMMITTEE ON BUSINESS/TRADE ........................................................................................ 149 9. SIXTH MEETING OF PAKISTAN AFGHANISTAN JOINT COMMITTEE ............ 170 10. UNIVERSITY -

MATCH UPDATES and TIME TABLE of Pakistan Super League 2021 S.NO
MATCH UPDATES AND TIME TABLE Of Pakistan Super League 2021 S.NO. Date Time (IST) Match Venue 1. February 20 7:30 PM Karachi Kings vs National Stadium, Quetta Gladiators Karachi 2. February 21 2:30 PM Islamabad United National Stadium, v Multan Sultans Karachi 3. February 21 7:30 PM Islamabad United National Stadium, v Multan Sultans Karachi 4. February 22 7:30 PM Lahore Qalandars National Stadium, vs Quetta Karachi Gladiators 5. February 23 7:30 PM Peshawar Zalmi National Stadium, vs Multan Sultans Karachi 6 February 24 7:30 PM Karachi Kings vs National Stadium, Islamabad United Karachi 7. February 26 2:30 PM Lahore Qalandars National Stadium, vs Multan Sultans Karachi 8. February 26 7:30 PM Peshawar Zalmi National Stadium, vs Quetta Karachi Gladiators 9. February 27 2:30 PM Karachi Kings vs National Stadium, Multan Sultans Karachi 10. February 27 7:30 PM Peshawar Zalmi National Stadium, vs Islamabad Karachi United 11. February 28 7:30 PM Karachi Kings vs National Stadium, Lahore Qalandars Karachi 12. March 1 7:30 PM Islamabad United National Stadium, vs Quetta Karachi Gladiators 13. March 3 2:30 PM Karachi Kings vs National Stadium, Peshawar Zalmi Karachi 14. March 3 7:30 PM Quetta Gladiators National Stadium, vs Multan Sultans Karachi 15. March 4 7:30 PM Lahore Qalandars National Stadium, vs Islamabad Karachi United 16 March 5 7:30 PM Multan Sultans vs National Stadium, Karachi Kings Karachi 17. March 6 2:30 PM Islamabad United National Stadium, v Quetta Karachi Gladiators 18. March 6 7:30 PM Peshawar Zalmi v National Stadium, Lahore Qalandars Karachi 19. -

P14 5 Layout 1
14 Established 1961 Sports Tuesday, March 27, 2018 Australian cricket faces huge backlash over ball-tampering Cricket Australia chief Sutherland rushing to S Africa SYDNEY: Sutherland was rushing to South Africa yes- Monday. “We know Australians want answers and we terday with the sport facing one of the toughest weeks will keep you updated on our findings and next steps, as in its history as a backlash grows over a ball-tampering a matter of urgency.” Smith and all members of the team scandal which is likely to cost Steve Smith the Test cap- will remain in South Africa to assist in the probe to taincy. Sponsors expressed “deep concern” as media determine exactly what happened, and who knew. and fans called for wide- Smith, whose talents with the spread changes and deci- bat have drawn breathless sive action following the comparisons with Aussie great shock admission that Smith Don Bradman, is not the only and senior team members man caught in the crosshairs. plotted to cheat in South Sponsors David Warner also stood Africa. Smith, 28, was down from his role as vice- removed from the captain- expressed captain, while questions remain cy for the remainder of the over coach Darren Lehmann third Test against South ‘deep concern’ although Smith said the former Africa on Sunday and was Australian international was not then banned for one match involved in the conspiracy. by the International Cricket Smith initially said the deci- Council (ICC). sion was made by the leader- His team’s weekend of ship group within the team, but shame then ended in a crushing 322-run rout. -

PCB Annual Report 2018-19
Designed by PRESTIGE Annual Report 2018-2019 ANNUAL REPORT 2018-2019 Contents Foreword Men's domestic cricket Chairman's Report 1 Regional Inter-District 2018-2019 65 Managing Director's Report 4 Quaid-e-Azam Trophy 67 Overview of men's international cricket 5 Quaid-e-Azam Trophy Grade-II 69 Overview of women’s international/domestic cricket 7 One-Day Cup for Regions and Departments 71 Overview of men's domestic cricket 9 Quaid-e-Azam One-Day Cup 73 Overview of women’s game development 11 National T20 Cup 75 Overview of the Academies' programmes 13 HBL PSL 2019 77 Obituaries 16 Pakistan Cup 83 Patron's Trophy Grade-II 85 Men's international cricket (2018-2019) Women's domestic cricket Asia Cup 2018 19 Inter-Departmental T20 Women's Cricket Championship 89 Pakistan vs Australia in the UAE 21 PCB Triangular One-Day Women’s Cricket Tournament 2018-19 91 Pakistan vs New Zealand in the UAE 25 Pakistan in South Africa 27 Pathways cricket Pakistan in England 31 U13 Regional National T20 Tournament 95 U16 Regional National One-Day Tournament 97 Men's international cricket U16 Pentangular One-Day Tournament 99 (2017-2018) Inter-Region U19 Three-Day Tournament 101 Independence Cup 2018 Pakistan vs World XI 35 Inter-Region U19 One-Day Tournament 103 Pakistan vs Sri Lanka in the UAE and Lahore 37 Pentangular U19 T20 Cup 105 Pakistan in New Zealand 39 Pakistan A vs New Zealand A and England Lions in the UAE 106 West Indies in Karachi 41 Pakistan U16 vs Australia U16 in the UAE 109 Pakistan tour of Ireland, England and Scotland 43 Pakistan U16 in Bangladesh -

PSL Eye: Predicting the Winning Team in Pakistan Super League (PSL) Matches PSL Eye: Predicting the Winning Team in Pakistan Super League (PSL) Matches
PSL Eye: Predicting the Winning Team in Pakistan Super League (PSL) Matches PSL Eye: Predicting the Winning Team in Pakistan Super League (PSL) Matches Muhammad Humza Siddiqui1 Muhammad Riaz2 Muhammad Nasir3 Uzma Afzal4 Sohaib Tariq5 Tariq Mahmood6 Abstract Pakistan Super League (PSL) is a well-known T20 cricket league with millions of viewers. With this large viewer base, predicting the outcome of PSL matches opens a new research avenue for academic researchers. In this paper, we collect PSL data from relevant sources and generate a validated data set for machine learning experiments. We implement the “PSL Eye” solution which employs Neural Networks (NNs) to predict the match winning team. We preprocess the dataset to eliminate the extra variables then we tune the hyper parameters of NN. After acquiring The overall accuracy of PSL-Eye with testing data set is 82% which is very promising and shows the optimalimportance values of NNof hyper in predicting parameters, PSL matchwe run outcome. our NN based PSL Eye to obtain the final results. Keywords Machine Learning : Pakistan Super League, T20, PSL, Prediction, Neural Networks, Tensorflow, Keras, 1 Introduction Cricket is a bat and ball game played between two teams. At the international level, cricket is played in three different formats, i.e., one-day, T20 (Twenty-20) and test matches. T20 is the most recent and shortened form of cricket restricted to 20 overs. It was introduced by the England and Wales Cricket Board (ECB) in 2003. Several T20 leagues started after 2007 ICC World T20 tournament. Bangladesh Premier League, Big Bash League, Indian Premier League, Pakistan Super League, and Caribbean Premier League are well known and successful T20 leagues[2][15][16]. -

Muslim Saints of South Asia
MUSLIM SAINTS OF SOUTH ASIA This book studies the veneration practices and rituals of the Muslim saints. It outlines the principle trends of the main Sufi orders in India, the profiles and teachings of the famous and less well-known saints, and the development of pilgrimage to their tombs in India, Pakistan and Bangladesh. A detailed discussion of the interaction of the Hindu mystic tradition and Sufism shows the polarity between the rigidity of the orthodox and the flexibility of the popular Islam in South Asia. Treating the cult of saints as a universal and all pervading phenomenon embracing the life of the region in all its aspects, the analysis includes politics, social and family life, interpersonal relations, gender problems and national psyche. The author uses a multidimen- sional approach to the subject: a historical, religious and literary analysis of sources is combined with an anthropological study of the rites and rituals of the veneration of the shrines and the description of the architecture of the tombs. Anna Suvorova is Head of Department of Asian Literatures at the Institute of Oriental Studies, Russian Academy of Sciences, Moscow. A recognized scholar in the field of Indo-Islamic culture and liter- ature, she frequently lectures at universities all over the world. She is the author of several books in Russian and English including The Poetics of Urdu Dastaan; The Sources of the New Indian Drama; The Quest for Theatre: the twentieth century drama in India and Pakistan; Nostalgia for Lucknow and Masnawi: a study of Urdu romance. She has also translated several books on pre-modern Urdu prose into Russian. -

PSL Schedule 2020 PDF Download
PSL Schedule 2020 PDF Download Date Matches Venue 20-Feb Quetta Gladiators vs Islamabad United Karachi 21-Feb Karachi Kings vs Peshawar Zalmi Karachi 21-Feb Lahore Qalandars vs Multan Sultans Lahore 22-Feb Quetta Gladiators vs Peshawar Zalmi Karachi 22-Feb Islamabad United vs Multan Sultans Lahore 23-Feb Karachi Kings vs Quetta Gladiators Karachi 23-Feb Lahore Qalandars vs Islamabad United Lahore 26-Feb Multan Sultans vs Peshawar Zalmi Multan 27-Feb Islamabad United vs Quetta Gladiators Rawalpindi 28-Feb Multan Sultans vs Karachi Kings Multan 28-Feb Peshawar Zalmi vs Lahore Qalandars Rawalpindi 29-Feb Multan Sultans vs Quetta Gladiaotrs Multan 29-Feb Islamabad United vs Peshawar Zalmi Rawalpindi 1-Mar Islamabad United vs Karachi Kings Rawalpindi 2-Mar Peshawar Zalmi vs Karachi Kings Rawalpindi 3-Mar Quetta Gladiaotrs V Lahore Qalandars Lahore 4-Mar Islamabad United vs Lahore Qalandars Lahore 5-Mar Peshawar Zalmi vs Quetta Gladiators Rawalpindi 6-Mar Karachi Kings vs Multan Sultans Lahore 7-Mar Peshawar Zalmi vs Islamabad United Rawalpindi 7-Mar Lahore Qalandars vs Quetta Gladiators Lahore 8-Mar Multan Sultans vs Islamabad United Rawalpindi 8-Mar Lahore Qalandars vs Karachi Kings Lahore 10-Mar Lahore Qalandars vs Peshawar Zalmi Lahore 11-Mar Quetta Gladiators vs Multan Sultans Lahore 12-Mar Karachi Kings vs Lahore Qalandars Karachi 13-Mar Peshawar Zalmi vs Multan Sultans Karachi 14-Mar Karachi Kings vs Islamabad United Karachi 15-Mar Multan Sultans vs Lahore Qalandars Lahore 15-Mar Quetta Gladiators vs Karachi Kings Karachi 17-Mar Qualifier: Team 1 vs Team 2 Karachi 18-Mar Eliminator 1: Team 3 vs Team 4 Lahore Eliminator 2: Eliminator Winner vs 20-Mar Lahore Qualifier Runner-UP 22-Mar Final Lahore. -
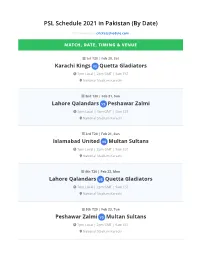
PSL Schedule 2021 in Pakistan (By Date)
PSL Schedule 2021 in Pakistan (By Date) Full coverage at cricketschedule.com MATCH, DATE, TIMING & VENUE 1st T20 | Feb 20, Sat Karachi Kings vs Quetta Gladiators 7pm Local | 2pm GMT | 9am EST National Stadium Karachi 2nd T20 | Feb 21, Sun Lahore Qalandars vs Peshawar Zalmi 2pm Local | 9am GMT | 4am EST National Stadium Karachi 3rd T20 | Feb 21, Sun Islamabad United vs Multan Sultans 7pm Local | 2pm GMT | 9am EST National Stadium Karachi 4th T20 | Feb 22, Mon Lahore Qalandars vs Quetta Gladiators 7pm Local | 2pm GMT | 9am EST National Stadium Karachi 5th T20 | Feb 23, Tue Peshawar Zalmi vs Multan Sultans 7pm Local | 2pm GMT | 9am EST National Stadium Karachi MATCH, DATE, TIMING & VENUE 6th T20 | Feb 24, Wed Karachi Kings vs Islamabad United 7pm Local | 2pm GMT | 9am EST National Stadium Karachi 7th T20 | Feb 26, Fri Lahore Qalandars vs Multan Sultans 3pm Local | 10am GMT | 5am EST National Stadium Karachi 8th T20 | Feb 26, Fri Peshawar Zalmi vs Quetta Gladiators 8pm Local | 3pm GMT | 10am EST National Stadium Karachi 9th T20 | Feb 27, Sat Karachi Kings vs Multan Sultans 2pm Local | 9am GMT | 4am EST National Stadium Karachi 10th T20 | Feb 27, Sat Peshawar Zalmi vs Islamabad United 7pm Local | 2pm GMT | 9am EST National Stadium Karachi 11th T20 | Feb 28, Sun Karachi Kings vs Lahore Qalandars 7pm Local | 2pm GMT | 9am EST National Stadium Karachi MATCH, DATE, TIMING & VENUE 12th T20 | Mar 01, Mon Islamabad United vs Quetta Gladiators 7pm Local | 2pm GMT | 9am EST National Stadium Karachi 13th T20 | Mar -

Islamabad United Announce JS Bank As Official Partners
Islamabad United Announce JS Bank as Official Partners JS Bank will be a main partner for Islamabad United for PSL 2 Lahore, 25 January 2017 – Islamabad United, the winners of the inaugural HBL PSL, is proud to announce its partnership with JS Bank as the principal sponsor of the franchise for the second season of the Pakistan Super League. The bank signs up as the franchise's “Official Partner” for the second season of the PSL. JS Bank is part of the JS Group, one of Pakistan’s most diversified and progressive financial services groups controlling and operating market-leading financial services companies in Pakistan across various sectors including commercial banking, asset management and securities brokerage. JS Bank currently operates 307 branches in 152 cities with one overseas branch in Bahrain and offers a diverse range of financial services. Regarding the partnership, JS Bank Marketing Head Imran Shaikh stated “It’s a pleasure to partner with an organization like Islamabad United who shares our vision for a better Pakistan and they have done a remarkable job, especially after having won the last Pakistan Super League in attracting others to this wonderful sport. Cricket has always been very close to JS Bank as we have been promoting cricket in the country since 2011. JS Bank has initiated various tournaments like JS Bank Women's T20, JS Bank Chairman’s Cricket Tournament and also supported the promotion of wheelchair cricket to provide opportunities for Pakistan’s youth to showcase their talent and skills at the highest level” Islamabad United owner Ali Naqvi added, "We are delighted to partner with one of Pakistan's leading banks. -

PSL 5 Schedule with Venue, Time, Date
Date Match PSL Team City Time 20th Feb 2020 Opening CeremonyQuetta Gladiator Vs Islamabad United Karachi Day 1st Match 21st Feb 2020 2nd Match Karachi Kings Vs Peshawar Zalmi Karachi Day 21st Feb 2020 3rd Match Lahore Qalandars Vs Multan Sultans Lahore Night 22nd Feb 2020 4th Match Quetta Gladiator Vs Peshawar Zalmi Karachi Day 22nd Feb 2020 5th Match Islamabad United Vs Multan Sultans Lahore Night 23rd Feb 2020 6th Match Karachi Kings Vs Quetta Gladiators Karachi Day 23rd Feb 2020 7th Match Lahore Qalandars Vs Islamabad United Lahore Night 26th Feb 2020 8th Match Multan Sultans Vs Peshawar Zalmi Multan Night 27th Feb 2020 9th Match Islamabad United Vs Quetta Gladiators Rawalpindi Night 28th Feb 2020 10th Match Multan Sultans Vs Karachi Kings Multan Day 28th Feb 2020 11th Match Peshawar Zalmi Vs Lahore Qalandars Rawalpindi Night 29th Feb 2020 12th Match Multan Sultans VS Quetta Gladiators Multan Day 29th Feb 2020 13th Match Islamabad United Vs Peshawar Zalmi Rawalpindi Night 1st March 2020 14th Match Islamabad United Vs Karachi Kings Rawalpindi Night 2nd March 202015th Match Peshawar Zalmi Vs Karachi Kings Rawalpindi Night 3rd March 202016th Match Quetta Gladiators Vs Lahore Qalandars Lahore Night 4th March 202017th Match Islamabad United Vs Lahore Qalandars Lahore Night 5th March 202018th Match Peshawar Zalmi Vs Quetta Gladiators Rawalpindi Night 6th March 202019th Match Karachi Kings Vs Multan Sultans Lahore Night 7th March 202020th Match Peshawar Zalmi Vs Islamabad United Rawalpindi Day 7th March 202021st Match Lahore Qalandars Vs Quetta -

January 2021 Volume 12 Issue 01 Promoting Bilateral Relations | Current Affairs | Trade & Economic Affairs | Education | Technology | Culture & Tourism ABC Certified
Monthly Magazine on National & International Political Affairs, Diplomatic Issues January 2021 Volume 12 Issue 01 Promoting Bilateral Relations | Current Affairs | Trade & Economic Affairs | Education | Technology | Culture & Tourism ABC Certified “Publishing from Pakistan, United Kingdom/EU & will be soon from UAE , Central Africa, Central Asia & Asia Pacific” Member APNS, CPNE Central Media List A Largest, Widely Circulated Diplomatic Magazine | www.diplomaticfocus.org | www.diplomaticfocus-uk.com | Member Diplomatic Council /diplomaticfocusofficial /dip_focus THE LEADING FORCE Atif Naeem Rana, CEO, Lahore Qalandars January 2021 Volume 12 Issue 01 “Publishing from Pakistan, United Kingdom/EU & will be soon from UAE ” 14 20 24 30 36 Further solidifying and expanding Paki- Pakistan and China have reiterated their resolve to further consolidate their friendship 14 for the mutual benefit of the two countries. This was discussed at a meeting between stan-China ties the visiting Chinese Minister for National Defence, General Wei Fenghe, and President Dr Arif Alvi, at Aiwan-e-Sadr. Welcoming the Chinese Defence Minister, the President said that Pakistan’s friendship with China was the cornerstone of its foreign policy and Pakistan wanted to further improve and cement its ties with the People’s Republic of China so as to address the security challenges being faced by the region. PRIME MINISTER IMRAN KHAN VISITS NAVAL Honourable Prime Minister of Pakistan, lmran Khan visited Naval Headquarters, 20 Islamabad. Upon arrival Prime Minister was welcomed by Chief of the Naval Staff, HEADQUARTERS Admiral Muhammad Amjad Khan Niazi and was presented Guard of Honour by a smartly turned out contingent. Prime Minister laid floral wreath at Shuhada monument and was introduced to the Principal Staff Officers at Naval Headquarters. -

Men's Global Employment Report 2020
FICA MEN’S PROFESSIONAL CRICKET GLOBAL EMPLOYMENT REPORT 2020 IT’S ESSENTIAL THE GLOBAL CRICKET STRUCTURE AND LEADERSHIP PROTECTS THE HISTORY OF THE GAME AND PLAYERS SHOULD BE ALSO ITS FUTURE. DOMESTIC ENCOURAGED TO SPEAK LEAGUES AND INTERNATIONAL UP ON BIG ISSUES IN SPORT CRICKET BOTH HAVE A REALLY AND SOCIETY. WITH STRONG IMPORTANT PLACE AND THERE LEADERSHIP CRICKET CAN BE NEEDS TO BE A BALANCE A GENUINE FORCE FOR GOOD. BETWEEN THEM. Jason Holder Eoin Morgan I WOULD LOVE TO SEE ONE OF THE THINGS OUR THE ROLE OF PLAYERS’ EYES HAVE BEEN OPENED TO ASSOCIATIONS EMBRACED SINCE FORMING A PLAYERS’ ACROSS THE WHOLE CRICKET ASSOCIATION... IS THAT PLAYERS WORLD. PLAYER VOICE IS ARE OFTEN THE ONES LEFT ON IMPORTANT TO PROTECTING THE END OF THE LINE WHEN BOTH PLAYERS AND THE GAME. LEAGUES FALL OVER OR WHEN IN MY EXPERIENCE PLAYERS CLUBS AND LEAGUES DON’T CARE DEEPLY ABOUT THE GAME HONOUR COMMITMENTS. WE AND WANT TO ENSURE IT’S HOPE THE ICC WORK WITH FICA HEALTHY AND THRIVING. TO PROPERLY ADDRESS THIS. Aaron Finch William Porterfield 2 THE FICA 2020 EMPLOYMENT REPORT 3 BACKGROUND AT THE TIME OF WRITING, THERE We know that structural issues, terms and conditions CRICKET SHOULD BE PROACTIVELY ARE MORE THAN 4191 REGISTERED of employment, and wage gaps all remain key drivers PROTECTING FUNDAMENTAL MEN’S PROFESSIONAL CRICKETERS of player employment decisions, particularly given there PLAYER RIGHTS AT GLOBAL LEVEL. is now an alternative, global domestic league market for IN THE WORLD. players to play in. We have also seen flexible and effective The ICC currently regulates the ‘sanctioned cricket’ A significant number of these, along with past players, arrangements implemented in several progressive framework, which purports to give it, and it’s members, are represented by FICA, and FICA’s member players’ countries to address some of the inherent issues the right to sanction cricket events in certain associations.