Watershed Modeling and Uncertainty Analysis For
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

List of TMDL Implementation Plans with Tmdls Organized by Basin
Latest 305(b)/303(d) List of Streams List of Stream Reaches With TMDLs and TMDL Implementation Plans - Updated June 2011 Total Maximum Daily Loadings TMDL TMDL PLAN DELIST BASIN NAME HUC10 REACH NAME LOCATION VIOLATIONS TMDL YEAR TMDL PLAN YEAR YEAR Altamaha 0307010601 Bullard Creek ~0.25 mi u/s Altamaha Road to Altamaha River Bio(sediment) TMDL 2007 09/30/2009 Altamaha 0307010601 Cobb Creek Oconee Creek to Altamaha River DO TMDL 2001 TMDL PLAN 08/31/2003 Altamaha 0307010601 Cobb Creek Oconee Creek to Altamaha River FC 2012 Altamaha 0307010601 Milligan Creek Uvalda to Altamaha River DO TMDL 2001 TMDL PLAN 08/31/2003 2006 Altamaha 0307010601 Milligan Creek Uvalda to Altamaha River FC TMDL 2001 TMDL PLAN 08/31/2003 Altamaha 0307010601 Oconee Creek Headwaters to Cobb Creek DO TMDL 2001 TMDL PLAN 08/31/2003 Altamaha 0307010601 Oconee Creek Headwaters to Cobb Creek FC TMDL 2001 TMDL PLAN 08/31/2003 Altamaha 0307010602 Ten Mile Creek Little Ten Mile Creek to Altamaha River Bio F 2012 Altamaha 0307010602 Ten Mile Creek Little Ten Mile Creek to Altamaha River DO TMDL 2001 TMDL PLAN 08/31/2003 Altamaha 0307010603 Beards Creek Spring Branch to Altamaha River Bio F 2012 Altamaha 0307010603 Five Mile Creek Headwaters to Altamaha River Bio(sediment) TMDL 2007 09/30/2009 Altamaha 0307010603 Goose Creek U/S Rd. S1922(Walton Griffis Rd.) to Little Goose Creek FC TMDL 2001 TMDL PLAN 08/31/2003 Altamaha 0307010603 Mushmelon Creek Headwaters to Delbos Bay Bio F 2012 Altamaha 0307010604 Altamaha River Confluence of Oconee and Ocmulgee Rivers to ITT Rayonier -

Analysis of Stream Runoff Trends in the Blue Ridge and Piedmont of Southeastern United States
Georgia State University ScholarWorks @ Georgia State University Geosciences Theses Department of Geosciences 4-20-2009 Analysis of Stream Runoff Trends in the Blue Ridge and Piedmont of Southeastern United States Usha Kharel Follow this and additional works at: https://scholarworks.gsu.edu/geosciences_theses Part of the Geography Commons, and the Geology Commons Recommended Citation Kharel, Usha, "Analysis of Stream Runoff Trends in the Blue Ridge and Piedmont of Southeastern United States." Thesis, Georgia State University, 2009. https://scholarworks.gsu.edu/geosciences_theses/15 This Thesis is brought to you for free and open access by the Department of Geosciences at ScholarWorks @ Georgia State University. It has been accepted for inclusion in Geosciences Theses by an authorized administrator of ScholarWorks @ Georgia State University. For more information, please contact [email protected]. ANALYSIS OF STREAM RUNOFF TRENDS IN THE BLUE RIDGE AND PIEDMONT OF SOUTHEASTERN UNITED STATES by USHA KHAREL Under the Direction of Seth Rose ABSTRACT The purpose of the study was to examine the temporal trends of three monthly variables: stream runoff, rainfall and air temperature and to find out if any correlation exists between rainfall and stream runoff in the Blue Ridge and Piedmont provinces of the southeast United States. Trend significance was determined using the non-parametric Mann-Kendall test on a monthly and annual basis. GIS analysis was used to find and integrate the urban and non-urban stream gauging, rainfall and temperature stations in the study area. The Mann-Kendall test showed a statistically insignificant temporal trend for all three variables. The correlation of 0.4 was observed for runoff and rainfall, which showed that these two parameters are moderately correlated. -

The Savannah River System L STEVENS CR
The upper reaches of the Bald Eagle river cut through Tallulah Gorge. LAKE TOXAWAY MIDDLE FORK The Seneca and Tugaloo Rivers come together near Hartwell, Georgia CASHIERS SAPPHIRE 0AKLAND TOXAWAY R. to form the Savannah River. From that point, the Savannah flows 300 GRIMSHAWES miles southeasterly to the Atlantic Ocean. The Watershed ROCK BOTTOM A ridge of high ground borders Fly fishermen catch trout on the every river system. This ridge Chattooga and Tallulah Rivers, COLLECTING encloses what is called a EASTATOE CR. SATOLAH tributaries of the Savannah in SYSTEM watershed. Beyond the ridge, LAKE Northeast Georgia. all water flows into another river RABUN BALD SUNSET JOCASSEE JOCASSEE system. Just as water in a bowl flows downward to a common MOUNTAIN CITY destination, all rivers, creeks, KEOWEE RIVER streams, ponds, lakes, wetlands SALEM and other types of water bodies TALLULAH R. CLAYTON PICKENS TAMASSEE in a watershed drain into the MOUNTAIN REST WOLF CR. river system. A watershed creates LAKE BURTON TIGER STEKOA CR. a natural community where CHATTOOGA RIVER ARIAIL every living thing has something WHETSTONE TRANSPORTING WILEY EASLEY SYSTEM in common – the source and SEED LAKEMONT SIX MILE LAKE GOLDEN CR. final disposition of their water. LAKE RABUN LONG CREEK LIBERTY CATEECHEE TALLULAH CHAUGA R. WALHALLA LAKE Tributary Network FALLS KEOWEE NORRIS One of the most surprising characteristics TUGALOO WEST UNION SIXMILE CR. DISPERSING LAKE of a river system is the intricate tributary SYSTEM COURTENAY NEWRY CENTRALEIGHTEENMILE CR. network that makes up the collecting YONAH TWELVEMILE CR. system. This detail does not show the TURNERVILLE LAKE RICHLAND UTICA A River System entire network, only a tiny portion of it. -
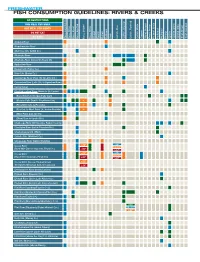
Fish Consumption Guidelines: Rivers & Creeks
FRESHWATER FISH CONSUMPTION GUIDELINES: RIVERS & CREEKS NO RESTRICTIONS ONE MEAL PER WEEK ONE MEAL PER MONTH DO NOT EAT NO DATA Bass, LargemouthBass, Other Bass, Shoal Bass, Spotted Bass, Striped Bass, White Bass, Bluegill Bowfin Buffalo Bullhead Carp Catfish, Blue Catfish, Channel Catfish,Flathead Catfish, White Crappie StripedMullet, Perch, Yellow Chain Pickerel, Redbreast Redhorse Redear Sucker Green Sunfish, Sunfish, Other Brown Trout, Rainbow Trout, Alapaha River Alapahoochee River Allatoona Crk. (Cobb Co.) Altamaha River Altamaha River (below US Route 25) Apalachee River Beaver Crk. (Taylor Co.) Brier Crk. (Burke Co.) Canoochee River (Hwy 192 to Lotts Crk.) Canoochee River (Lotts Crk. to Ogeechee River) Casey Canal Chattahoochee River (Helen to Lk. Lanier) (Buford Dam to Morgan Falls Dam) (Morgan Falls Dam to Peachtree Crk.) * (Peachtree Crk. to Pea Crk.) * (Pea Crk. to West Point Lk., below Franklin) * (West Point dam to I-85) (Oliver Dam to Upatoi Crk.) Chattooga River (NE Georgia, Rabun County) Chestatee River (below Tesnatee Riv.) Chickamauga Crk. (West) Cohulla Crk. (Whitfield Co.) Conasauga River (below Stateline) <18" Coosa River <20" 18 –32" (River Mile Zero to Hwy 100, Floyd Co.) ≥20" >32" <18" Coosa River <20" 18 –32" (Hwy 100 to Stateline, Floyd Co.) ≥20" >32" Coosa River (Coosa, Etowah below <20" Thompson-Weinman dam, Oostanaula) ≥20" Coosawattee River (below Carters) Etowah River (Dawson Co.) Etowah River (above Lake Allatoona) Etowah River (below Lake Allatoona dam) Flint River (Spalding/Fayette Cos.) Flint River (Meriwether/Upson/Pike Cos.) Flint River (Taylor Co.) Flint River (Macon/Dooly/Worth/Lee Cos.) <16" Flint River (Dougherty/Baker Mitchell Cos.) 16–30" >30" Gum Crk. -

NATIONAL FORESTS /// the Southern Appalachians
NATIONAL FORESTS /// the Southern Appalachians NORTH CAROLINA SOUTH CAROLINA, TENNESSEE » » « « « GEORGIA UNITED STATES DEPARTMENT OF AGRICULTURE FOREST SERVICE National Forests in the Southern Appalachians UNITED STATES DEPARTMENT OE AGRICULTURE FOREST SERVICE SOUTHERN REGION ATLANTA, GEORGIA MF-42 R.8 COVER PHOTO.—Lovely Lake Santeetlah in the iXantahala National Forest. In the misty Unicoi Mountains beyond the lake is located the Joyce Kilmer Memorial Forest. F-286647 UNITED STATES GOVERNMENT PRINTING OEEICE WASHINGTON : 1940 F 386645 Power from national-forest waters: Streams whose watersheds are protected have a more even flow. I! Where Rivers Are Born Two GREAT ranges of mountains sweep southwestward through Ten nessee, the Carolinas, and Georgia. Centering largely in these mountains in the area where the boundaries of the four States converge are five national forests — the Cherokee, Pisgah, Nantahala, Chattahoochee, and Sumter. The more eastern of the ranges on the slopes of which thesefo rests lie is the Blue Ridge which rises abruptly out of the Piedmont country and forms the divide between waters flowing southeast and south into the Atlantic Ocean and northwest to the Tennessee River en route to the Gulf of Mexico. The southeastern slope of the ridge is cut deeply by the rivers which rush toward the plains, the top is rounded, and the northwestern slopes are gentle. Only a few of its peaks rise as much as a mile above the sea. The western range, roughly paralleling the Blue Ridge and connected to it by transverse ranges, is divided into segments by rivers born high on the slopes between the transverse ranges. -

Stream-Temperature Charcteristics in Georgia
STREAM-TEMPERATURE CHARACTERISTICS IN GEORGIA U.S. GEOLOGICAL SURVEY Prepared in cooperation with the GEORGIA DEPARTMENT OF NATURAL RESOURCES ENVIRONMENTAL PROTECTION DIVISION Water-Resources Investigations Report 96-4203 STREAM-TEMPERATURE CHARACTERISTICS IN GEORGIA By T.R. Dyar and S.J. Alhadeff ______________________________________________________________________________ U.S. GEOLOGICAL SURVEY Water-Resources Investigations Report 96-4203 Prepared in cooperation with GEORGIA DEPARTMENT OF NATURAL RESOURCES ENVIRONMENTAL PROTECTION DIVISION Atlanta, Georgia 1997 U.S. DEPARTMENT OF THE INTERIOR BRUCE BABBITT, Secretary U.S. GEOLOGICAL SURVEY Charles G. Groat, Director For additional information write to: Copies of this report can be purchased from: District Chief U.S. Geological Survey U.S. Geological Survey Branch of Information Services 3039 Amwiler Road, Suite 130 Denver Federal Center Peachtree Business Center Box 25286 Atlanta, GA 30360-2824 Denver, CO 80225-0286 CONTENTS Page Abstract . 1 Introduction . 1 Purpose and scope . 2 Previous investigations. 2 Station-identification system . 3 Stream-temperature data . 3 Long-term stream-temperature characteristics. 6 Natural stream-temperature characteristics . 7 Regression analysis . 7 Harmonic mean coefficient . 7 Amplitude coefficient. 10 Phase coefficient . 13 Statewide harmonic equation . 13 Examples of estimating natural stream-temperature characteristics . 15 Panther Creek . 15 West Armuchee Creek . 15 Alcovy River . 18 Altamaha River . 18 Summary of stream-temperature characteristics by river basin . 19 Savannah River basin . 19 Ogeechee River basin. 25 Altamaha River basin. 25 Satilla-St Marys River basins. 26 Suwannee-Ochlockonee River basins . 27 Chattahoochee River basin. 27 Flint River basin. 28 Coosa River basin. 29 Tennessee River basin . 31 Selected references. 31 Tabular data . 33 Graphs showing harmonic stream-temperature curves of observed data and statewide harmonic equation for selected stations, figures 14-211 . -

Chattooga Quarterly
Chattooga Quarterly WWinterinter ♦♦♦♦♦♦ 22018018 / 22019019 T G George Cooke’s 1841 painting showcases three waterfalls of Tallulah Gorge. Artwork c/o GA Museum of Art, UGA; Gift of Mrs. William Lorenzo Moss I N S I D E Director’s Page..............................................2 The Drought of 1925.....................................7 Trillium persistens.........................................3 Watershed Update........................................12 Tallulah Gorge...............................................4 Members’ Pages...........................................17 2 Chattooga Quarterly Director’s Page Nicole Hayler might be a reasonable forestry project. However, there are several issues that we're concerned about: A literal tsunami swept over the Chattooga River during 2018, in the form of record-breaking, relentless rainfall throughout • Front and center is the use of clear-cuts, which is the much of the watershed. Now looking ahead, I fear that a even-age tree harvesting technique that the Forest Service fi gurative tsunami may befall the Chattooga watershed in 2019. is expected to use on 1,400 acres. Clearcutting is an For an inkling of what this might be, see this publication’s extremely heavy-handed forestry treatment, which causes “watershed update” section: Cashiers Lake development, major habitat disruption and destruction. The denuded Nantahala-Pisgah Forest Plan Revision, Foothills Landscape lands are also much more susceptible to developing erosion project, loblolly pine clearcutting, and sedimentation issues. -

Mercury Contamination of Stream Sediment in North Georgia from Former Gold Mines in the Dahlonega Gold Belt
MERCURY CONTAMINATION OF STREAM SEDIMENT IN NORTH GEORGIA FROM FORMER GOLD MINES IN THE DAHLONEGA GOLD BELT David S. Leigh AUTHOR: Assistant Professor, Department of Geography, The University of Georgia, Athens, Georgia 30602-2502; e-mail; dleigh @ uga.ce.ug a.edu. REFERENCE: Proceedings of the 1995 Georgia Water Resources Conference, held April 11 and 12, 1995, at The University of Georgia, Kathryn J. Hatcher, Editor, Carl Vinson Institute of Government, The University of Georgia, Athens, Georgia. Abstract. Floodplain sediments downstream from 19th century gold mining sites were studied to determine if mining • activities released toxic metals into streams. Mercury was I e found to be the only significant mining pollutant, and it results .k I from the use of mercury to amalgamate and recover gold from rah stamp mills and sluices. Sediment-bound mercury in mining- ,- ,_4awsonvilki 7r— -Ban Grand Dahlonega ' related sediment ranges from 0.01 to 10.0 mg/kg, whereas ci Gold Belt natural background concentrations range from 0.01 to 0.06 1 , ....,,,,•-■ i '''---... ....... ,.., '2,., mg/kg. Mercury content decreases with increasing distance ; ,.-\ '',.-- from former mines, and only the sites in very close proximity ......,_ ( .f. ' '.,_--.J . ` ,./.' * i . \ \ ,,,K '>• .7. to mines contain "hazardous" levels of mercury in sediments. , „..atiarat,L , 1 1 \ i '---;--" --------rt, Limited data indicate that some mercury is released to stream I . 'II' i..,, ! ..1../ il .\ ): . ■ water in the mining district. ----t -, , / Figure 1. Map of the Dahlonega Gold Belt and locations INTRODUCTION referenced in the text. The objective of this research was to assess the magnitude mined area included the Yahoola Creek-Chestatee River and spatial distribution of trace metals in floodplain sediments watershed immediately south and east of Dahlonega, Georgia associated with former gold mining activity in the Dahlonega along a 20 km long stream segment that terminates in Lake Gold Belt of north Georgia. -

2021 Trout Stocking Frequencies
2021 Trout Stocking Information The Georgia Wildlife Resources Division stocks trout in the streams, rivers and small lakes listed below. Trout stocking begins in March and continues through October. The stocking frequency of each waterbody listed below is based on the following: area available, fishing pressure, and summer water temperatures. Notes: The tables below are grouped by stocking frequency and include water body name and the county in which it is located. Asterisks ( * ) indicate a variation from the main heading of each group. Table 1. Stocked weekly from April through July, then twice before Labor Day, and once in the fall (September/October). Water body County Water body County Boggs Creek Lumpkin Nottely River** Union Blue Ridge Tailwaters Fannin Panther Creek* Stephens Chattahoochee River White Rock Creek Fannin Cooper Creek Union Sarah's Creek Rabun Dicks Creek Lumpkin Smith Creek White Etowah River** Lumpkin Soapstone Creek** Towns Holly Creek Murray Soque River Habersham Jasus Creek White Tallulah River Rabun Forsyth, Lanier Tailwaters Tallulah River Towns Gwinnett Low Gap Creek White Toccoa River** Fannin Middle Fork Broad R.* Stephens Warwoman Creek Rabun Moccasin Creek Rabun West Fork Chattooga Rabun Nimblewill Creek** Lumpkin Wildcat Creek Rabun * Stocked weekly until July 4th, not stocked afterward. ** Stocked weekly until July 4th, twice monthly afterward. georgiawildlife.com/fishing/trout Published: 3/29/2021 Table 2. Stocked twice each month from April through July. Water body County Water body County Amicalola -

CSRA Regionally Important Resources Plan
CENTRAL SAVANNAH RIVER AREA REGIONAL COMMISSION Regionally Important Resources Plan Contents Introduction ........................................................................................................................................4 Methodology .......................................................................................................................................4 Natural Resources ..............................................................................................................................7 Natural Resources: Parks & Forested Areas .............................................................................9 Magnolia Springs State Park ................................................................................................. 11 Elijah Clark State Park ............................................................................................................ 12 A.H. Stephens Memorial State Park ..................................................................................... 13 Hamburg State Park ................................................................................................................ 14 Mistletoe State Park ................................................................................................................ 15 Natural Resources: Wildlife Management Areas .................................................................. 17 Clarks Hill Wildlife Management Area ............................................................................... 18 Di-Lane -

Characterization of Temporal and Spatial Variability of Turbidity in the Upper Chattahoochee River
CHARACTERIZATION OF TEMPORAL AND SPATIAL VARIABILITY OF TURBIDITY IN THE UPPER CHATTAHOOCHEE RIVER Skelly A. Holmbeck-Pelhaml and Todd C. Rasmussen' AUTHORS: 'Graduate Student and 'Assistant Professor, School of Forest Resources, The University of Georgia, Athens, Georgia 30602. REFERENCE: Proceedings of the 1997 Georgia Water Resources Conference, held March 20-22, 1997, at The University of Georgia, Kathryn J. Hatcher, Editor, Institute of Ecology, The University of Georgia, Athens, Georgia. Abstract. Our objective is to develop the information geologic structures. necessary for establishing a regulatory basis for sediment The lower part of Lanier's drainage area is in the Atlanta control. We present sediment data at four USGS monitoring Plateau. The land and channel slopes in this area are not as stations in the Upper Chattahoochee River Watershed. The steep as those in the Dahlonega plateau. Both areas have a data show that TSS is a strong function of discharge. A unique similar climate, with moderate temperatures and an average relationship between TSS and discharge is found for all annual precipitation greater than 60 inches. Winter and early stations when the discharge is normalized by its long-term spring months are the wettest (Faye et al., 1980). mean. With this regional relationship, we can establish a baseline for comparing watersheds as a function of discharge. METHODS INTRODUCTION Data used for this paper were obtained from U.S. Geological Survey (USGS) sources. Suspended sediment concentrations Suspended sediment loads in the Chattahoochee River above and discharges were given for four streams: the Chattahoochee Atlanta are a concern to water resources managers from a River at Cornelia, the West Fork of the Little River, the multitude of perspectives. -

PROPOSED Atlantic Sturgeon Critical Habitat Rivers in the Southeast U.S. 30°N Florida 80°W 75°W Table 1
80°W 75°W Virginia Ü 0 25 50 100 150 200 Miles C1 North Carolina C2 C3 35°N 35°N CU1 C4 South Carolina Carolina DPS Units C1 Roanoke River, NC CU2 C5 C6 C2 Tar-Pamlico River, NC Georgia C3 Neuse River, NC C4 Cape Fear River, NC Northeast Cape Fear River, NC SA1 SAU1 CU1 Cape Fear River, NC C7 C5 Pee Dee River, SC Waccamaw River, SC SA2 South Atlantic DPS Units Bull Creek, SC SA3 SA1 Edisto River, SC C6 Black River, SC SA4 North Fork Edisto River, SC C7 Santee River, SC South Fork Edisto River, SC Rediversion Canal, SC SA5 North Edisto River, SC North Santee River, SC South Edisto River, SC South Santee River, SC SA2 Combahee River, SC Tailrace Canal-W Cooper River, SC Salkehatchie, River, SC Cooper River, SC SA6 SA3 Savannah River, SC/GA CU2 Wateree River, SC SAU1 Savannah River, SC/GA Congaree River, SC SA4 Ogeechee River, GA Broad River, SC SA5 Altamaha River, GA Santee River, above L Marion, SC Oconee River, GA Lake Marion, SC SA7 Ocmulgee River, GA Diversion Canal, SC SA6 Satilla River, GA Lake Moultrie, SC SA7 St. Marys, GA/FL Rediversion Canal, SC 30°N PROPOSED Atlantic Sturgeon Critical Habitat Rivers in the Southeast U.S. 30°N Florida 80°W 75°W Table 1. Proposed Critical Habitat Units and Extents of the Units. Critical Habitat Unit Name DPS Nomenclature Water Body State Upper extent River kilometers River miles Roanoke Carolina Unit 1 (C1) Roanoke River North Carolina Roanoke Rapids Dam 213 132 Tar ‐ Pamlico Carolina Unit 2 (C2) Tar ‐ Pamlico River North Carolina Rocky Mount Mill Pond Dam 199 124 Neuse Carolina Unit 3 (C3) Neuse River North Carolina Milburnie Dam 345 214 Cape Fear Carolina Unit 4 (C4) Cape Fear River North Carolina Lock and Dam #2 151 94 Northeast Cape Fear River North Carolina Upstream side of Rones Chapel Road Bridge 218 136 Cape Fear Unoccupied Carolina Unoccupied Unit 1 (CU1) Cape Fear River North Carolina Huske Lock and Dam (a.k.a.