DOCSLIB.ORG

Essays on the Forecasting Power of Implied Volatility Prithviraj Shyamal Banerjee

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Essays on the Forecasting Power of Implied Volatility Prithviraj Shyamal Banerjee Florida State University Libraries Electronic Theses, Treatises and Dissertations The Graduate School 2008 Essays on the Forecasting Power of Implied Volatility Prithviraj Shyamal Banerjee Follow this and additional works at the FSU Digital Library. For more information, please contact [email protected] FLORIDA STATE UNIVERSITY COLLEGE OF BUSINESS ESSAYS ON THE FORECASTING POWER OF IMPLIED VOLATILITY By PRITHVIRAJ SHYAMAL BANERJEE A Dissertation submitted to the Department of finance in partial fulfillment of the requirements for the degree of Doctor of Philosophy Degree Awarded: Spring Semester, 2008 The members of the Committee approve the Dissertation of Prithviraj Shyamal Banerjee defended on March 18, 2008. Dr. David R. Peterson Professor Directing Dissertation Dr. Thomas Zuehlke Outside Committee Member Dr. William Christiansen Committee Member Dr. James S. Doran Committee Member Dr. Danling Jiang Committee Member Approved: Caryn Beck-Dudley, Dean, College of Business The Office of Graduate Studies has verified and approved the above named committee members. ii I dedicate this work to my parents iii ACKNOWLEDGEMENTS I gratefully acknowledge the immense help and guidance of my Chair, Dr. David R. Peterson, from whom I have learnt to do research. I also gratefully acknowledge the help of my other committee members, especially Dr. James Doran and Dr. Danling Jiang, and my uncle Dr. Tarun K Mukherjee, who has helped me more times than I can thank him for. iv TABLE OF CONTENTS List of Tables ............................................................................................vii List of Figures ............................................................................................xi Abstract .................................................................................................xii 1. Introduction ............................................................................................1 2. Implied Volatility and Future Portfolio Returns...........................................11 3. The Forecasting Power of the Risk and Sentiment Components of Implied Volatility ....................................................................47 4. Forecasting Future Portfolio Volatility: The Role of Risk and Sentiment Components of Implied Volatility and other Forecast ......................................112 v REFERENCES ............................................................................................ 164 BIOGRAPHICAL SKETCH ........................................................................... 170 vi LIST OF TABLES Table 1: Estimates from 22-Day and 44-Day Future Market Returns Regressed on VIX ...............................................................................35 Table 2: Regression Estimates for the Fama-French 25 Portfolios Sorted on Book-to-Market Equity and Size .................................35 Table 3: Regression Estimates for the Fama-French 25 Portfolios Sorted on Book-to-Market Equityand Size, Including Four Factors as Independent Variables .............................................................37 Table 4: Descriptive Statistics ..........................................................................38 Table 5: Return Regression Estimates for the Twelve Portfolios Sorted on Book-to-Market Equity, Size, and Beta ............................................39 Table 6: 22-Day Regression Estimates for the Twelve Portfolios Sorted on Book-to-Market Equity, Size, and Beta ............................................41 Table 7: 44-Day Regression Estimates for the Twelve Portfolios Sorted on Book-to-Market Equity, Size, and Beta ...........................................42 Table 8: Return Regression Estimates using High VIX Level Observations ..........................................................................................44 Table 9: 22-Day and 44-Day Regression Estimates of the Four Factors on VIX ..............................................................................45 Table 10: Descriptive Statistics .......................................................................66 Table 11: Regression Estimates of the Raw Sentiment Proxies on Risk Factors ................................................................................70 Table 12: Regression Estimates of VIX on the Orthogonal Sentiment Proxies ............................................................................................73 Table 13: Regression Estimates of 22-day and 44-day Future Returns of Portfolios on VIX............................................................................73 vii Table 14: Regression Estimates of 22-day Future Returns of Portfolios on VIXRISK....................................................................................79 Table 15: Regression Estimates of VIX on the Risk Measures..........................86 Table 16: Regression Estimates of 22-day Future Returns of Portfolios on VIXSENT ............................................................................................87 Table 17: Regression Estimates of 22-day Future Returns of Portfolios on VIXRISK and VIXSENT ............................................................................93 Table 18: Regression Estimates of 22-day and 44-day Future Returns of Portfolios on VIXRISK and the Orthogonal Sentiment Measures.................100 Table 19: Tabulation of Significant Variables with Signs in Table 9.................111 Table 20: Regression Estimates of 22-day Realized Standard Deviation of Portfolios on VIX.........................................................................................127 Table 21: Regression Estimates of 22-day Realized Standard Deviation of Portfolios on Lagged Market Standard Deviation.........................................130 Table 22: Regression Estimates of 22-day Realized Standard Deviation of Portfolios on VIX and Lagged Market Standard Deviation...........................133 Table 23: Regression Estimates of 22-day Realized Standard Deviation of Portfolios on VIXRISK, Lagged Portfolio Standard Deviation, and Lagged Market Standard Deviation............................................................136 Table 24: Regression Estimates of 22-day Realized Standard Deviation of Portfolios on VIXRISK, GARCH Forecast, and Lagged Market Standard Deviation............................................................140 Table 25: Regression Estimates of 22-day Realized Standard Deviation of Portfolios on VIXSENT, Lagged Portfolio Standard Deviation, and Lagged Market Standard Deviation............................145 Table 26: Regression Estimates of 22-day Realized Standard Deviation of Portfolios on VIXSENT, GARCH Forecast, and Lagged Market Standard Deviation ..............................148 viii Table 27: Regression Estimates of 22-day Realized Standard Deviation of Portfolios on VIXRISK, VIXSENT, Lagged Portfolio Standard Deviation, and Lagged Market Standard Deviation .............153 Table 28: Regression Estimates of 22-day Realized Standard Deviation of Portfolios on VIXRISK, VIXSENT, GARCH Forecast, and Lagged Market Standard Deviation ............................................158 ix LIST OF FIGURES Figure 1: Mean Returns for the 12 B/M, Size and Beta Portfolios.....................34 x ABSTRACT In this dissertation, I look at the forecasting power of implied volatility. I decompose implied volatility into a risk component and a sentiment component, and examine the forecasting power of these components for future returns and volatilities of portfolios sorted by important firm characteristics. I find that the forecasting power of implied volatility for returns is higher for higher beta portfolios and for longer horizon holding periods. I also find that the sentiment component of implied volatility has more (less) forecasting power for future returns (volatility) than the risk component. xi CHAPTER 1 INTRODUCTION The Black and Scholes (1973) model implies a one-to-one correspondence between the price of the option and the volatility of the underlying asset. By inverting the option price and using an algorithmic procedure we can back out the volatility, which is called the implied volatility for the asset1. If markets are efficient, the implied volatility of the asset is the market’s best guess of the underlying asset’s volatility over the remaining life of the option. Past studies involving implied volatility have focused on things like its properties and its reaction to events. Especially important is that prior studies analyze implied volatility’s forecasting power for future realized volatility and to a lesser extent, for future realized returns. Poterba and Summers (1986) and Diz and Finucane (1993) find that implied volatility has a mean reverting component. Stein (1989) finds that long-term options “overreact” to changes in the implied volatility of short-term options. Poteshman (2001) finds evidence of under reaction to changes in contemporaneous instantaneous variance and overreaction to increasing or decreasing variance over the prior few days. Event studies of implied volatility examine the reaction of implied volatility to corporate events. Patell and Wolfson (1981) find that implied volatility falls after earnings announcements. French and Dubofsky (1986) find that implied volatility increases with stock splits, whereas Klein and Peterson (1988) find no response of implied volatility to stock splits2. Implied volatility functions have also been used to obtain the risk neutral densities of the underlying asset (Campa, Chang and Reider (1998),
Load more

Recommended publications
  • 07/20/21 1 the All New Market Analysis Tim Ord, Editor 16928 Van
    07/20/21 The All New Market Analysis Tim Ord, Editor 16928 Van Dorn Street Walton, Nebraska 68461 www.ord-oracle.com (402) 413-0980 . [email protected] SPX Monitoring purposes; Sold 7/20/21 SPX 4325= gain .08%; long SPX 6/28/21 at 4290.61. Monitoring purposes GOLD: Long GDX on 10/9/20 at 40.78. Long Term SPX monitor purposes; Neutral We have "800" phone update that cost $6.00 per call, and billed to a credit card. Call (1-970-586-4760) for sign up. We update Eastern Time at 9:45 and 4:10. Question? Call (402) 413-0980. Yesterday we said, “CNN Fear Creed indicator closed 18 (https://money.cnn.com/data/fear-and-greed/ ); readings below 20 have marked lows and at least near lows in the past. The 2 day TRIN closed today at 3.37; reading above 3.00 are bullish. The TRIN is showing there is panic in the market. Also the tick closed at -209 and the TRIN closed at 1.58 today and that combination has been bullish short term. Today’s surge in volume suggests a “Selling Climax”. Most likely there will be a bounce short term that may find resistance on today’s down gap. If the 1 Signals are provided as general information only and are not investment recommendations. You are responsible for your own investment decisions. Past performance does not guarantee future performance. Opinions are based on historical research and data believed reliable, there is no guarantee results will be profitable. Not responsible for errors or omissions.
    [Show full text]
  • Active Portfolio Management
    Active Portfolio Management Charting • Technical analysts are sometimes called chartists because they study records or charts of past stock-prices and trading volume, hoping to find patterns they can exploit to make a profit. • We examine next several specific charting strategies. Christos A. Ioannou 2/27 The Dow Theory • The Dow Theory, named after its creator Charles Dow (who established The Wall Street Journal), is the grandfather of most technical analysis. • The aim of the Dow theory is to identify long-term trends in stock market prices. • The two indicators used are the Dow Jones Industrial Average (DJIA) and the Dow Jones Transportation Average (DJTA). The DJIA is the key indicator of underlying trends, while the DJTA usually serves as a check to confirm or reject that signal. Christos A. Ioannou 3/27 The Dow Theory (Cont.) The Dow theory posits three forces simultaneously affecting stock prices: 1 The primary trend is the long-term movement of prices, lasting from several months to several years. 2 Secondary or intermediate trends are caused by short-term deviations of prices from the underlying trend line. These deviations are eliminated via corrections when prices revert back to trend values. 3 Tertiary or minor trends are daily fluctuations of little importance. Christos A. Ioannou 4/27 bod10773_ch19.qxd 11/12/2002 11:37 AM Page 661 19 Behavioral Finance and Technical Analysis 661 The Dow Theory The Dow theory, named after its creator Charles Dow (who established The Wall Street Jour- Dow theory nal), is the grandfather of most technical analysis. While most technicians today would view A technique that the theory as dated, the approach of many more statistically sophisticated methods are essen- attempts to discern tially variants of Dow’s approach.
    [Show full text]
  • Top 7 Market Breadth Indicators for Day Traders
    Top 7 Market Breadth Indicators for Day Traders Day trading at the end of the day comes down to timing. Funny how the smaller the time frame you trade, the more accuracy is required of you the trader. I cannot tell you how many times I opened a position 5 minutes too soon or closed a minute early. We are literally talking about seconds here and the difference between a profitable or losing trade. To help improve timing, day traders will heavily rely on time and sales and level 2. However, understanding how the broad market is moving can help you stay on the right side of the market. For example, if you were long a stock in the Nikkei the night of the 2016 presidential election results came in with Trump as the winner, you were just blindsided. It wasn’t that you picked the wrong stock or anything. The Nikkei shot lower across the board due to the election results, only to rally by the close. Well, in this article we will cover these market breadth indicators and how you can use them to improve the accuracy of your trading. Top 7 Market Breadth Indicators for Day Traders It’s not an official TradingSim post if we do not provide a top 10 list. #1 – TICK Index The TICK Index is a measurement of the short-term bias of the overall market and is one of the most important tools for day trading. It measures the difference between the number of stocks on the NYSE that have registered an uptick versus the number of stocks that have registered a downtick.
    [Show full text]
  • Investing with Volume Analysis
    Praise for Investing with Volume Analysis “Investing with Volume Analysis is a compelling read on the critical role that changing volume patterns play on predicting stock price movement. As buyers and sellers vie for dominance over price, volume analysis is a divining rod of profitable insight, helping to focus the serious investor on where profit can be realized and risk avoided.” —Walter A. Row, III, CFA, Vice President, Portfolio Manager, Eaton Vance Management “In Investing with Volume Analysis, Buff builds a strong case for giving more attention to volume. This book gives a broad overview of volume diagnostic measures and includes several references to academic studies underpinning the importance of volume analysis. Maybe most importantly, it gives insight into the Volume Price Confirmation Indicator (VPCI), an indicator Buff developed to more accurately gauge investor participation when moving averages reveal price trends. The reader will find out how to calculate the VPCI and how to use it to evaluate the health of existing trends.” —Dr. John Zietlow, D.B.A., CTP, Professor of Finance, Malone University (Canton, OH) “In Investing with Volume Analysis, the reader … should be prepared to discover a trove of new ground-breaking innovations and ideas for revolutionizing volume analysis. Whether it is his new Capital Weighted Volume, Trend Trust Indicator, or Anti-Volume Stop Loss method, Buff offers the reader new ideas and tools unavailable anywhere else.” —From the Foreword by Jerry E. Blythe, Market Analyst, President of Winthrop Associates, and Founder of Blythe Investment Counsel “Over the years, with all the advancements in computing power and analysis tools, one of the most important tools of analysis, volume, has been sadly neglected.
    [Show full text]
  • The Complete Guide to Market Breadth Indicators 00Morris-FM 8/11/05 5:57 PM Page Ii 00Morris-FM 8/11/05 5:57 PM Page Iii
    00Morris-FM 8/11/05 5:57 PM Page i The Complete Guide to Market Breadth Indicators 00Morris-FM 8/11/05 5:57 PM Page ii 00Morris-FM 8/11/05 5:57 PM Page iii The Complete Guide to Market Breadth Indicators How to Analyze and Evaluate Market Direction and Strength Gregory L. Morris McGraw-Hill New York Chicago San Francisco Lisbon London Madrid Mexico City Milan New Delhi San Juan Seoul Singapore Sydney Toronto 00Morris-FM 8/11/05 5:57 PM Page iv Copyright © 2006 by The McGraw-Hill Companies. All rights reserved. Printed in the United States of America. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or dis- tributed in any form or by any means, or stored in a data base or retrieval sys- tem, without the prior written permission of the publisher. 1 2 3 4 5 6 7 8 9 0 DOC/DOC 0 9 8 7 6 ISBN 0-07-144443-2 McGraw-Hill books are available at special quantity discounts to use as pre- miums and sales promotions, or for use in corporate training programs. For more information, please write to the Director of Special Sales, Professional Publishing, McGraw-Hill, Two Penn Plaza, New York, NY 10121-2298. Or con- tact your local bookstore. This publication is designed to provide accurate and authoritative information in regard to the subject matter covered. It is sold with the understanding that neither the author nor the publisher is engaged in rendering legal, accounting, or other professional service.
    [Show full text]
  • Get in and out of Trades at the Right Time
    A $79 Value! Get In and Out of Trades at the Right Time Sponsored by: 1. A Candle Trigger for Market Bottoms 3 2. A Candle Trigger for Market Tops 8 Powered by: 3. Profiting from Multiple Time Frame Sector Analysis 13 4. Volume Always Precedes Price 18 Get In and Out of Trades at the Right Time By Tom Aspray Technician Get In and Out of Trades at the Right Time Japanese rice traders have used technical analysis and candlestick charts since the 17th century. Many traders spend so much time trying to remember the often complex names given to the individual candle chart formations that they miss the trade. The different names often cause confusion as they are not able to determine whether they should be buying or selling. One of the simplest candle formations is the doji which is formed when the open and closing price are close to the same. In A Candle Trigger for Market Bottoms and A Candle Trigger for Market Tops I discuss the two very reliable doji trading setups John Person developed. After using candle charts for over 25 years I have found his method for generating doji-based buy or sell signals to be the most reliable candle chart setups I have ever encountered. I have stressed the importance of only buying stocks that are performing better than the S&P 500 for quite some time. For those who trade the short side of the market, choosing the stocks that are acting weaker than the S&P 500 is the best strategy.
    [Show full text]
  • The Boundaries of Technical Analysis Milton W
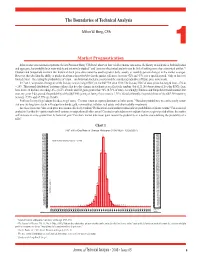
    The Boundaries of Technical Analysis Milton W. Berg, CFA 1 Market Prognostication In his treatise on stock market patterns, the late Professor Harry V. Roberts1 observed that “of all economic time series, the history of stock prices, both individual and aggregate, has probably been most widely and intensively studied,” and “patterns of technical analysis may be little if nothing more than a statistical artifact.”2 Ibbotson and Sinquefield maintain that historical stock price data cannot be used to predict daily, weekly or monthly percent changes in the market averages. However, they do claim the ability to predict in advance the probability that the market will move between +X% and -Y% over a specific period.3 Only to this very limited extent – forecasting the probabilities of return – can historical stock price movements be considered indicative of future price movements. In Chart 1, we present a histogram of the five-day rate of change (ROC) in the S&P 500 since 1928. The five-day ROC of stock prices has ranged from -27% to + 24%. This normal distribution4 is strong evidence that five-day changes in stock prices are effectively random. Out of 21,165 observations of five-day ROCs, there have been 138 declines exceeding -8%, (0.65% of total) and 150 gains greater than +8% (0.71% of total). Accordingly, Ibbotson and Sinquefield would maintain that over any given 5-day period, the probability of the S&P 500 gaining or losing 8% or more is 1.36%. Stated differently, the probabilities of the S&P 500 returning between -7.99% and +7.99% are 98.64%.
    [Show full text]
  • The Titans of Technical Analysis by David Penn REAL WORLD
    Stocks & Commodities V. 20:10 (32-38): The Titans Of Technical Analysis by David Penn REAL WORLD A Celebration Of Technical Analysts From Dow To Zweig The Titans Of Technical Analysis A not-so-random walk through the history of charting the observations, and commentary on the subjects of trading markets. and technical analysis. From our earliest issues featuring reviews titled “An Easy Course In Using The HP-12C And by David Penn Other Financial Calculators” to the present issue, which includes pages of Traders’ Tips in sophisticated computer any years ago, a poet friend who was editing language, no other publication has had its finger on the pulse a collection of contemporary verse noted to of both applied and theoretical technical analysis for as long me that “about half the working poets in as STOCKS & COMMODITIES. And this has been no mere M America are going to be really upset about minding the store. this anthology. Of course, the other half of them are in the S&C publisher Jack Hutson introduced the TRIX, or triple book. …” exponential smoothing oscillator, in 1983. The Richard Such sentiments came to mind when I embarked upon the Wyckoff method was reintroduced to the world via these task of highlighting the few among the many whose contri- pages in 1986. John Bollinger, Jack Schwager, and Vic butions to the field of technical analysis have made them Sperandeo were all among S&C’s interviews in 1993. In the what STOCKS & COMMODITIES has designated the “Titans nine-odd years since then, as a bull market in equities resumed, Of Technical Analysis.” S&C was on hand to provide technical tools for minimizing How subjective is such a list? In some ways, all too risk and maximizing gain — whether through new indicators subjective — particularly with those whose contributions (such as John Ehlers’ MESA adaptive moving averages), new are more recent or are less widely enjoyed.
    [Show full text]
  • In a Follow-Up to Our February Interview with Trader Linda Raschke
    Active TRADER Interview In a follow-up to our February interview with trader Linda Raschke, we discuss more of the indicators and strategies she uses each day. BY MARK ETZKORN she uses now, such as the “3-10” oscillator (see “Indicator checklist,” p. 78), are essentially the same ones she picked up from her original mentor more than 20 years ago. Raschke says trading “upstairs” required some adjustment, although initially everything progressed well enough. Relying ou can take the trader away from the floor, but solely on a Quotron screen (a simple price quote display that you can’t take the floor away from the trader. was prevalent in the 1980s), Raschke says she racked up 45suc- Case in point, Linda Raschke. cessive profitable weeks, in part because the technology was so YRaschke, who currently trades privately and runs a real-time conducive to the tape reading skills she had honed on the online trading room (see “Linda Raschke keeps up the pace,” exchange floor. But when she got her first analysis software in February 2004, p. 66), started as an options floor trader on the 1987, she lost money for three months. Pacific Coast Stock Exchange in 1981, then followed that with “It was a distraction in a way,” she says. “It was like a tennis a stint at the Philadelphia Stock Exchange. player who’s always played on clay switching to grass.” Although it has been 17 years since she left the pits and Setbacks and limitations don’t typically make compelling switched to off-floor trading, Raschke says the market princi- trading stories, but Raschke is fairly open about past missteps ples and analysis techniques she developed during those days and trading realities, including the fact that she went bust early remain integral to her trading today.
    [Show full text]
  • Technical Analytics SOFTWARE HIGHLIGHTS
    Technical Analytics SOFTWARE HIGHLIGHTS IB Technical Analytics consists of real-time charts and scanners so you can view and filter Quick Glance data to react quickly to market activity. Real-time charts display up to a year of daily market data with 15 technical studies. TWS Market Scanners evaluate real-time market activity for contracts matching your filter criteria. Both the charts and scanners uniquely Real-time Charts include options analytic indicators that help you identify trading opportunities in the stock • 1 minute to 1 month and options markets. • Line, Bar or Candlesticks Interactive Charts New! - Chart Volatilities • Choose Bar, Line or Candlestick • Time period 1 minute to 1 year • Available intervals 5 second to 1 day ChartTrader Create and manage orders all within the chart feature Chart Volatilities - New! • Historical Volatility • Option Implied Volatility • Option Open Interest • Option Volume Chart Studies • Moving Averages: • Simple Display a real-time line, bar or candlestick chart for any contract on your trading page, including cur- • Weighted rencies. Use the chart to initiate orders based on trends or patterns you observe, even chart volatilities • Exponential • Bollinger Bands • Envelopes Real-time charts • Parabolic SAR Line, bar or candlestick real-time charts for any contract on your trading page. • Relative Strength Index Set time parameters, draw trendlines, view time and sales, and even submit orders • MACD -- all from the TWS real-time Charts feature. • ADX/DMI Chart Trader • Stochastic Oscillator Create orders directly on an intraday chart using the Chart Trader panel. Order • On Balance Volume management tabs located under the Quote Panel allow you to transmit or modify • Rate of Change orders, log activity, view executions and review changes to the portfolio.
    [Show full text]
  • Information Spillover from VIX Options to VIX Futures: the Information Content of Put-Call Ratio and Implied Volatility Skew
    Stockholm School of Economics Department of Finance Master of Science in Finance Master Thesis - Double Degree Program Information Spillover from VIX Options to VIX Futures: the Information Content of Put-Call Ratio and Implied Volatility Skew Giorgio Magagnotti May 2016 Abstract: This paper investigates the predictive power of the information content of VIX options with respect to VIX futures. Two sub-samples of variables are used in the analysis: put-call ratios of daily option volumes and spreads among implied volatilities across different moneyness levels, derived from VIX options prices. The statistical significance and the forecasting accuracy of various predictive models are back-tested through the computation of one-day ahead out-of-sample forecasts, using both expanding and rolling estimation windows. Different statistical indicators are employed to identify the best performing models. The results indicate that put-call ratio and implied volatility skew variables possess predictive power with respect to VIX futures, and their combined inclusion improves the forecasting accuracy. Supervisor: Prof. Paolo Sodini Key words: VIX futures, VIX options, put-call ratio, implied volatility skew Aknowledgements I deeply thank my supervisor Prof. Paolo Sodini for his advices, support and supervision throughout all the steps of this work. I also owe my gratitude to Prof. Francesco Saita, for his interest in the topic, his mentoring and his patience. a Erica a Ivan 2 INDEX 1. INTRODUCTION 3 2. VIX INDEX, FUTURES AND OPTIONS 5 2.1. VIX index 5 2.2. VIX futures 7 2.3. VIX options 10 3. LITERATURE REVIEW 11 3.1. Option volume and put-call ratio 11 3.2.
    [Show full text]
  • Guide to Effective Daytrading
    The Wizetraders’ Guide to Effective Day Trading Mel Raiman, Ph.D. Copyright © 2003 by Melvyn L. Raiman ALL RIGHTS RESERVED This publication may be reproduced or trasmitted by e-mail for personal use. Permission for commercial use must be requested from the copyright holder. The information and suggestions expressed in this publication are the personal opionions of Melvyn L. Raiman and have not been endorsed by the manfufacturer of Wizetrade and WizeFinder. This information is being provided to users of Wizetrade at their request for their personal use and Melvyn L. Raiman assumes no respon- sibility for their trading results. Since there are many vairables inherent in day trading including the skill level of the individual trader, his or her ability to interpret Wizetrade charts, the direction of the market, the execution of the trader’s broker, and the trading characteristics of a particular stock, it must be assumed that there will be a range of success rates when applying any trading system. Foreword I had the pleasure of speaking about day trading at WizeFEST 2002. After the convention I prepared a small document addressing the subject of proxy Wizemen and have since received numerous phone calls and e-mails. First of all, there is obviously considerable interest in day trading. Sec- ondly, based upon the questions that I am asked over and over, traders want very specific answers to a multitude of questions. The purpose of this expanded publication is to answer many of these questions which I receive daily. It’s really a short course in day trading with Wizetrade, and it is my sincere desire to bring everyone up to speed in the art of day trading.
    [Show full text]