Growth Efficiency and Temperature in Scallops
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Shell Matrix of the European Thorny Oyster, Spondylus Gaederopus: Microstructural and Molecular Characterization
The shell matrix of the european thorny oyster, Spondylus gaederopus: microstructural and molecular characterization. Jorune Sakalauskaite, Laurent Plasseraud, Jérôme Thomas, Marie Alberic, Mathieu Thoury, Jonathan Perrin, Frédéric Jamme, Cédric Broussard, Beatrice Demarchi, Frédéric Marin To cite this version: Jorune Sakalauskaite, Laurent Plasseraud, Jérôme Thomas, Marie Alberic, Mathieu Thoury, et al.. The shell matrix of the european thorny oyster, Spondylus gaederopus: microstructural and molecular characterization.. Journal of Structural Biology, Elsevier, 2020, 211 (1), pp.107497. 10.1016/j.jsb.2020.107497. hal-02906399 HAL Id: hal-02906399 https://hal.archives-ouvertes.fr/hal-02906399 Submitted on 17 Nov 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. The shell matrix of the European thorny oyster, Spondylus gaederopus: microstructural and molecular characterization List of authors: Jorune Sakalauskaite1,2, Laurent Plasseraud3, Jérôme Thomas2, Marie Albéric4, Mathieu Thoury5, Jonathan Perrin6, Frédéric Jamme6, Cédric Broussard7, Beatrice Demarchi1, Frédéric Marin2 Affiliations 1. Department of Life Sciences and Systems Biology, University of Turin, Via Accademia Albertina 13, 10123 Turin, Italy; 2. Biogeosciences, UMR CNRS 6282, University of Burgundy-Franche-Comté, 6 Boulevard Gabriel, 21000 Dijon, France. 3. Institute of Molecular Chemistry, ICMUB UMR CNRS 6302, University of Burgundy- Franche-Comté, 9 Avenue Alain Savary, 21000 Dijon, France. -

Genomic Signatures of G-Protein-Coupled Receptor
Genomic signatures of G-protein-coupled royalsocietypublishing.org/journal/rspb receptor expansions reveal functional transitions in the evolution of cephalopod signal transduction Research Elena A. Ritschard1,2, Robert R. Fitak2, Oleg Simakov1 and So¨nke Johnsen2 Cite this article: Ritschard EA, Fitak RR, Simakov O, Johnsen S. 2019 Genomic 1Department of Molecular Evolution and Development, University of Vienna, Vienna, Austria 2Department of Biology, Duke University, Durham, NC, USA signatures of G-protein-coupled receptor expansions reveal functional transitions in the EAR, 0000-0002-4956-9703; RRF, 0000-0002-7398-6259; OS, 0000-0002-3585-4511; SJ, 0000-0002-3943-8320 evolution of cephalopod signal transduction. Proc. R. Soc. B 286: 20182929. Coleoid cephalopods show unique morphological and neural novelties, such http://dx.doi.org/10.1098/rspb.2018.2929 as arms with tactile and chemosensory suckers and a large complex nervous system. The evolution of such cephalopod novelties has been attributed at a genomic level to independent gene family expansions, yet the exact associ- ation and the evolutionary timing remain unclear. In the octopus genome, Received: 26 December 2018 one such expansion occurred in the G-protein-coupled receptors (GPCRs) Accepted: 4 February 2019 repertoire, a superfamily of proteins that mediate signal transduction. Here, we assessed the evolutionary history of this expansion and its relationship with cephalopod novelties. Using phylogenetic analyses, at least two cepha- lopod- and two octopus-specific GPCR expansions were identified. Signatures of positive selection were analysed within the four groups, and Subject Category: the locations of these sequences in the Octopus bimaculoides genome were Genetics and genomics inspected. -

List of Bivalve Molluscs from British Columbia, Canada
List of Bivalve Molluscs from British Columbia, Canada Compiled by Robert G. Forsyth Research Associate, Invertebrate Zoology, Royal BC Museum, 675 Belleville Street, Victoria, BC V8W 9W2; [email protected] Rick M. Harbo Research Associate, Invertebrate Zoology, Royal BC Museum, 675 Belleville Street, Victoria BC V8W 9W2; [email protected] Last revised: 11 October 2013 INTRODUCTION Classification rankings are constantly under debate and review. The higher classification utilized here follows Bieler et al. (2010). Another useful resource is the online World Register of Marine Species (WoRMS; Gofas 2013) where the traditional ranking of Pteriomorphia, Palaeoheterodonta and Heterodonta as subclasses is used. This list includes 237 bivalve species from marine and freshwater habitats of British Columbia, Canada. Marine species (206) are mostly derived from Coan et al. (2000) and Carlton (2007). Freshwater species (31) are from Clarke (1981). Common names of marine bivalves are from Coan et al. (2000), who adopted most names from Turgeon et al. (1998); common names of freshwater species are from Turgeon et al. (1998). Changes to names or additions to the fauna since these two publications are marked with footnotes. Marine groups are in black type, freshwater taxa are in blue. Introduced (non-indigenous) species are marked with an asterisk (*). Marine intertidal species (n=84) are noted with a dagger (†). Quayle (1960) published a BC Provincial Museum handbook, The Intertidal Bivalves of British Columbia. Harbo (1997; 2011) provided illustrations and descriptions of many of the bivalves found in British Columbia, including an identification guide for bivalve siphons and “shows”. Lamb & Hanby (2005) also illustrated many species. -

Japan Update to 05.04.2021 Approval No Name Address Products Number FROZEN CHUM SALMON DRESSED (Oncorhynchus Keta)
Japan Update to 05.04.2021 Approval No Name Address Products Number FROZEN CHUM SALMON DRESSED (Oncorhynchus keta). FROZEN DOLPHINFISH DRESSED (Coryphaena hippurus). FROZEN JAPANESE SARDINE ROUND (Sardinops 81,Misaki-Cho,Rausu- Kaneshin Tsuyama melanostictus). FROZEN ALASKA POLLACK DRESSED (Theragra chalcogramma). 1 VN01870001 Cho, Menashi- Co.,Ltd FROZEN ALASKA POLLACK ROUND (Theragra chalcogramma). FROZEN PACIFIC COD Gun,Hokkaido,Japan DRESSED. (Gadus macrocephalus). FROZEN PACIFIC COD ROUND. (Gadus macrocephalus) Maekawa Shouten Hokkaido Nemuro City Fresh Fish (Excluding Fish By-Product); Fresh Bivalve Mollusk.; Frozen Fish (Excluding 2 VN01860002 Co., Ltd Nishihamacho 10-177 Fish By-Product); Frozen Processed Bivalve Mollusk; Frozen Chum Salmon(Round,Dressed,Semi-Dressed,Fillet,Head,Bone,Skin); Frozen 1-35-1 Alaska Pollack(Round,Dressed,Semi-Dressed,Fillet); Frozen Pacific Taiyo Sangyo Co.,Ltd. 3 VN01840003 Showachuo,Kushiro- Cod(Round,Dressed,Semi-Dressed,Fillet); Frozen Pacific Saury(Round,Dressed,Semi- Kushiro Factory City,Hokkaido,Japan Dressed); Frozen Chub Mackerel(Round,Fillet); Frozen Blue Mackerel(Round,Fillet); Frozen Salted Pollack Roe 3-9 Komaba- Taiyo Sangyo Co.,Ltd. 4 VN01860004 Cho,Nemuro- Frozen Fish ; Frozen Processed Fish; (Excluding By-Product) Nemuro Factory City,Hokkaido,Japan 3-2-20 Kitahama- Marutoku Abe Suisan 5 VN01920005 Cho,Monbetu- Frozen Chum Salmon Dressed; Frozen Salmon Dressed Co.,Ltd City,Hokkaido,Japan Frozen Chum Salmon(Round,Semi-Dressed,Fillet); Frozen Salmon Milt; Frozen Pink Salmon(Round,Semi-Dressed,Dressed,Fillet); -
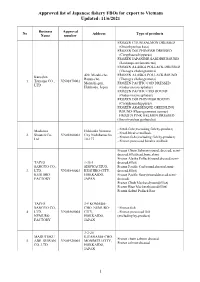
Approved List of Japanese Fishery Fbos for Export to Vietnam Updated: 11/6/2021
Approved list of Japanese fishery FBOs for export to Vietnam Updated: 11/6/2021 Business Approval No Address Type of products Name number FROZEN CHUM SALMON DRESSED (Oncorhynchus keta) FROZEN DOLPHINFISH DRESSED (Coryphaena hippurus) FROZEN JAPANESE SARDINE ROUND (Sardinops melanostictus) FROZEN ALASKA POLLACK DRESSED (Theragra chalcogramma) 420, Misaki-cho, FROZEN ALASKA POLLACK ROUND Kaneshin Rausu-cho, (Theragra chalcogramma) 1. Tsuyama CO., VN01870001 Menashi-gun, FROZEN PACIFIC COD DRESSED LTD Hokkaido, Japan (Gadus macrocephalus) FROZEN PACIFIC COD ROUND (Gadus macrocephalus) FROZEN DOLPHIN FISH ROUND (Coryphaena hippurus) FROZEN ARABESQUE GREENLING ROUND (Pleurogrammus azonus) FROZEN PINK SALMON DRESSED (Oncorhynchus gorbuscha) - Fresh fish (excluding fish by-product) Maekawa Hokkaido Nemuro - Fresh bivalve mollusk. 2. Shouten Co., VN01860002 City Nishihamacho - Frozen fish (excluding fish by-product) Ltd 10-177 - Frozen processed bivalve mollusk Frozen Chum Salmon (round, dressed, semi- dressed,fillet,head,bone,skin) Frozen Alaska Pollack(round,dressed,semi- TAIYO 1-35-1 dressed,fillet) SANGYO CO., SHOWACHUO, Frozen Pacific Cod(round,dressed,semi- 3. LTD. VN01840003 KUSHIRO-CITY, dressed,fillet) KUSHIRO HOKKAIDO, Frozen Pacific Saury(round,dressed,semi- FACTORY JAPAN dressed) Frozen Chub Mackerel(round,fillet) Frozen Blue Mackerel(round,fillet) Frozen Salted Pollack Roe TAIYO 3-9 KOMABA- SANGYO CO., CHO, NEMURO- - Frozen fish 4. LTD. VN01860004 CITY, - Frozen processed fish NEMURO HOKKAIDO, (excluding by-product) FACTORY JAPAN -

Molecular Identification of Steroidogenesis-Related Genes in Scallops and Their Potential Roles in Gametogenesis
View metadata, citation and similar papers at core.ac.uk brought to you by CORE Molecular identification of steroidogenesis-related genes in scallops and their potential roles in gametogenesis 著者 Tongchai Thitiphuree, Kazue Nagasawa, Makoto Osada journal or The Journal of Steroid Biochemistry and publication title Molecular Biology volume 186 page range 22-23 year 2019-02 URL http://hdl.handle.net/10097/00128371 doi: 10.1016/j.jsbmb.2018.09.004 Creative Commons : 表示 - 非営利 - 改変禁止 http://creativecommons.org/licenses/by-nc-nd/3.0/deed.ja The Journal of Steroid Biochemistry and Molecular Biology, Vol.186 (2019) [DOI: 10.1016/j.jsbmb.2018.09.004] Molecular identification of steroidogenesis-related genes in scallops and their potential roles in gametogenesis Tongchai THITIPHUREE *1, Kazue NAGASAWA *1, Makoto OSADA *1 *1 Laboratory of Aquacultural Biology, Graduate School of Agricultural Science, Tohoku University, 468-1 Aoba, Aramaki, Aoba-ku, Sendai, Miyagi, Japan Abstract Sex steroids are crucial for controlling gametogenesis and germ cell maturation in vertebrates. It has been proposed that Yesso scallop (Mizuhopecten yessoensis) has the same sex steroids as those animals, but the scallop biosynthetic pathway is unclear. In this study, we characterized several steroidogenesis-related genes in M. yessoensis and proposed a putative biosynthetic pathway for sex steroids that is similar to that of vertebrates. Specifically, we identified several steroidogenesis-related gene sequences that encode steroid metabolizing enzymes: StAR-related lipid transfer (START) protein, 17α-hydroxylase, 17,20-lyase (cyp17a), 17β-hydroxysteroid dehydrogenase (hsd17b), and 3β-hydroxysteroid dehydrogenase (hsd3b). We sampled adult scallops throughout their reproductive phase to compare their degree of maturation with their intensity of mRNA expression. -

The Evolution of Extreme Longevity in Modern and Fossil Bivalves
Syracuse University SURFACE Dissertations - ALL SURFACE August 2016 The evolution of extreme longevity in modern and fossil bivalves David Kelton Moss Syracuse University Follow this and additional works at: https://surface.syr.edu/etd Part of the Physical Sciences and Mathematics Commons Recommended Citation Moss, David Kelton, "The evolution of extreme longevity in modern and fossil bivalves" (2016). Dissertations - ALL. 662. https://surface.syr.edu/etd/662 This Dissertation is brought to you for free and open access by the SURFACE at SURFACE. It has been accepted for inclusion in Dissertations - ALL by an authorized administrator of SURFACE. For more information, please contact [email protected]. Abstract: The factors involved in promoting long life are extremely intriguing from a human perspective. In part by confronting our own mortality, we have a desire to understand why some organisms live for centuries and others only a matter of days or weeks. What are the factors involved in promoting long life? Not only are questions of lifespan significant from a human perspective, but they are also important from a paleontological one. Most studies of evolution in the fossil record examine changes in the size and the shape of organisms through time. Size and shape are in part a function of life history parameters like lifespan and growth rate, but so far little work has been done on either in the fossil record. The shells of bivavled mollusks may provide an avenue to do just that. Bivalves, much like trees, record their size at each year of life in their shells. In other words, bivalve shells record not only lifespan, but also growth rate. -

The Gene-Rich Genome of the Scallop Pecten Maximus Nathan J
GigaScience, 9, 2020, 1–13 doi: 10.1093/gigascience/giaa037 Data Note Downloaded from https://academic.oup.com/gigascience/article/9/5/giaa037/5827190 by FMC Corporation Librarian user on 02 June 2021 DATA NOTE The gene-rich genome of the scallop Pecten maximus Nathan J. Kenny1,2, Shane A. McCarthy3, Olga Dudchenko4,5, Katherine James1,6, Emma Betteridge7,CraigCorton7, Jale Dolucan7,8, Dan Mead7, Karen Oliver7, Arina D. Omer4, Sarah Pelan7, Yan Ryan9,10, Ying Sims7, Jason Skelton7, Michelle Smith7, James Torrance7, David Weisz4, Anil Wipat9, Erez L Aiden4,5,11,12, Kerstin Howe7 and Suzanne T. Williams 1,* 1Natural History Museum, Department of Life Sciences, Cromwell Road, London SW7 5BD, UK; 2Present address: Oxford Brookes University, Headington Road, Oxford OX3 0BP, UK; 3University of Cambridge, Department of Genetics, Cambridge CB2 3EH, UK; 4The Center for Genome Architecture, Department of Molecular and Human Genetics, Baylor College of Medicine, Houston, TX 77030, USA; 5The Center for Theoretical Biological Physics, Rice University, 6100 Main St, Houston, TX 77005-1827, USA; 6Present address: Department of Applied Sciences, Faculty of Health and Life Sciences, Northumbria University, Newcastle upon Tyne NE1 8ST, UK; 7Wellcome Sanger Institute, Cambridge CB10 1SA, UK; 8Present address: Freeline Therapeutics Limited, Stevenage Bioscience Catalyst, Gunnels Wood Road, Stevenage, Hertfordshire, SG1 2FX, UK; 9School of Computing, Newcastle University, Newcastle upon Tyne NE1 7RU, UK; 10Institute of Infection and Global Health, Liverpool University, iC2, 146 Brownlow Hill, Liverpool L3 5RF, UK; 11Shanghai Institute for Advanced Immunochemical Studies, Shanghai Tech University, Shanghai, China and 12School of Agriculture and Environment, University of Western Australia, Perth, Australia. -

Petricolaria Pholadiformis Crepidula Fornicata (Victoria) Spartina Anglica Cecina Manchurica (Nanaimo) Intertidal NIS in BC – Plants / Algae
Distribution of Non-indigenous Intertidal Species on the Pacific Coast of Canada Graham E. Gillespie, Antan C. Phillips, Debbie L. Paltzat and Tom W. Therriault Pacific Biological Station Nanaimo, BC, Canada Acknowledgements • Sylvia Behrens Yamada (Oregon State University) • Susan Bower (Fisheries and Oceans Canada) • Jason Dunham (Fisheries and Ocean Canada) • Rick Harbo (Fisheries and Oceans Canada) Introduction • Non-indigenous species (NIS) are of concern globally – PICES WG on NIS – Canadian government programs to collect, synthesize and distribute data on NIS – Survey work to determine distribution and abundance of intertidal NIS • Strait of Georgia (Jamieson, Therriault) • Other areas of British Columbia Objectives • Provide updated information on distribution of intertidal NIS on the Pacific Coast of Canada • Synthesize information on distribution, source and pathway Legend and Data Sources • White circles ○are survey locations • Yellow circles ● are collection records from: – Other survey databases (limited species) – Literature and public records • Red circles ● are collection records from: – Exploratory intertidal clam surveys 1990-present – Exploratory NIS surveys 2006 Boundary Bay • Sole location for: • Primary location for: Crassostrea virginica Urosalpinx cinerea Crepidula convexa (Ladysmith) Nassarius fraterculus Neotrapezium liratum Nassarius obsoletus (Ladysmith) Petricolaria pholadiformis Crepidula fornicata (Victoria) Spartina anglica Cecina manchurica (Nanaimo) Intertidal NIS in BC – Plants / Algae • Wireweed, Sargassum -
Directional Sensitivity of the Japanese Scallop Mizuhopecten Yessoensis and Swift Scallop Chlamys Swifti to Water-Borne Vibrations
See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/226111056 Directional sensitivity of the Japanese scallop Mizuhopecten yessoensis and Swift scallop Chlamys swifti to water-borne vibrations Article in Russian Journal of Marine Biology · January 2005 DOI: 10.1007/s11179-005-0040-7 CITATIONS READS 11 88 1 author: Petr Zhadan Pacific Oceanological Institute 56 PUBLICATIONS 345 CITATIONS SEE PROFILE All content following this page was uploaded by Petr Zhadan on 17 June 2015. The user has requested enhancement of the downloaded file. Russian Journal of Marine Biology, Vol. 31, No. 1, 2005, pp. 28–35. Original Russian Text Copyright © 2005 by Biologiya Morya, Zhadan. PHYSIOLOGICAL ECOLOGY Directional Sensitivity of the Japanese Scallop Mizuhopecten yessoensis and Swift Scallop Chlamys Swifti to Water-Borne Vibrations P. M. Zhadan Pacific Oceanological Institute, Far East Division, Russian Academy of Sciences, Vladivostok, 690041 Russia e-mail: [email protected] Received January 29, 2004 Abstract—Behavioral experiments were conducted on two bivalve species—the Japanese scallop Mizu- hopecten yessoensis and the Swift scallop Chlamys swifti—to elucidate the role of their abdominal sense organ (ASO) in directional sensitivity to water-borne vibrations. The thresholds were determined at 140 Hz. Both spe- cies displayed the highest sensitivity to vibrations, the source of which was placed above the animal (opposite to the left valve), rostro-dorsally to its vertical axis. Removal of the ASO led to loss of directional sensitivity and a considerable increase in the sound reaction threshold. Both species were sensitive to modulated ultrasonic vibrations in the range of 30–1000 Hz. -

The Gene-Rich Genome of the Scallop Pecten Maximus Nathan J
GigaScience, 9, 2020, 1–13 doi: 10.1093/gigascience/giaa037 Data Note DATA NOTE The gene-rich genome of the scallop Pecten maximus Nathan J. Kenny1,2, Shane A. McCarthy3, Olga Dudchenko4,5, Katherine James1,6, Emma Betteridge7,CraigCorton7, Jale Dolucan7,8, Dan Mead7, Karen Oliver7, Arina D. Omer4, Sarah Pelan7, Yan Ryan9,10, Ying Sims7, Jason Skelton7, Michelle Smith7, James Torrance7, David Weisz4, Anil Wipat9, Erez L Aiden4,5,11,12, Kerstin Howe7 and Suzanne T. Williams 1,* 1Natural History Museum, Department of Life Sciences, Cromwell Road, London SW7 5BD, UK; 2Present address: Oxford Brookes University, Headington Road, Oxford OX3 0BP, UK; 3University of Cambridge, Department of Genetics, Cambridge CB2 3EH, UK; 4The Center for Genome Architecture, Department of Molecular and Human Genetics, Baylor College of Medicine, Houston, TX 77030, USA; 5The Center for Theoretical Biological Physics, Rice University, 6100 Main St, Houston, TX 77005-1827, USA; 6Present address: Department of Applied Sciences, Faculty of Health and Life Sciences, Northumbria University, Newcastle upon Tyne NE1 8ST, UK; 7Wellcome Sanger Institute, Cambridge CB10 1SA, UK; 8Present address: Freeline Therapeutics Limited, Stevenage Bioscience Catalyst, Gunnels Wood Road, Stevenage, Hertfordshire, SG1 2FX, UK; 9School of Computing, Newcastle University, Newcastle upon Tyne NE1 7RU, UK; 10Institute of Infection and Global Health, Liverpool University, iC2, 146 Brownlow Hill, Liverpool L3 5RF, UK; 11Shanghai Institute for Advanced Immunochemical Studies, Shanghai Tech University, Shanghai, China and 12School of Agriculture and Environment, University of Western Australia, Perth, Australia. ∗Correspondence address. Suzanne T. Williams, Department of Life Sciences, Natural History Museum, Cromwell Road, London SW7 5BD, UK. E-mail: [email protected] http://orcid.org/0000-0003-2995-5823 Abstract Background: The king scallop, Pecten maximus, is distributed in shallow waters along the Atlantic coast of Europe. -

Hydrophilic Shell Matrix Proteins of Nautilus Pompilius and the Identification of a Core Set of Conchiferan Domains
bioRxiv preprint doi: https://doi.org/10.1101/2020.11.14.382804; this version posted November 16, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. Short Title Shell Matrix Proteins of Nautilus pompilius Full Title Hydrophilic Shell Matrix Proteins of Nautilus pompilius and The Identification of a Core Set of Conchiferan Domains Authors Davin H. E. Setiamarga1,2,3,*, Kazuki Hirota1,10, Masa-aki Yoshida4, Yusuke Takeda3,5, Keiji Kito6, Keisuke Shimizu2,7, Yukinobu Isowa2,8, Kazuho Ikeo9, Takenori Sasaki3, Kazuyoshi Endo2 Authors Affiliations 1 Department of Applied Chemistry and Biochemistry, National Institute of Technology (KOSEN), Wakayama College, Gobo, Wakayama, Japan 644-0023 2 Graduate School of Sciences, The University of Tokyo, Bunkyo, Tokyo, Japan 113- 0033 3 The University Museum, The University of Tokyo, Tokyo, Japan 113-0033 4 Marine Biological Science Section, Education and Research Center for Biological Resources, Faculty of Life and Environmental Science, Shimane University, Oki, Shimane, Japan 685-0024 5 Graduate School of Science, Hokkaido University, Sapporo, Japan 060-0808 6 Department of Life Sciences, School of Agriculture, Meiji University, Kawasaki, Kanagawa, Japan 214-8571 7 Graduate School of Agriculture and Life Sciences, The University of Tokyo, Yayoi, Tokyo, Japan 113-8657 8 Shimoda Marine Research Center, University of Tsukuba, Shimoda, Shizuoka, Japan 411-8540 9 Center for Information Biology, National Institute of Genetics, Japan 411-8540 10 Present Address: Department of Biotechnology and Life Science, Tokyo University of Agriculture and Technology, Koganei, Tokyo, Japan 184-0012 bioRxiv preprint doi: https://doi.org/10.1101/2020.11.14.382804; this version posted November 16, 2020.