A Set-By-Set Analysis Method for Predicting the Outcome of Professional Singles Tennis Matches
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Cadenza Document
Player Profile & Performance - WASHINGTON DC WASHINGTON DC, USA, DC JULY 30 - AUGUST 5, 2018 | USD $250,000 INTERNATIONAL All data as at Monday, 30 Jul 2018 MAGDA LINETTE DOB Feb 12, 1992 (26) Residence Poznan, Poland Plays Right-handed (two-handed backhand) 62 Height 5' 7" (1.71 m) Singles Prize Career $1,605,562 Ranking Prize YTD $326,752 Career High Singles Rank 55 (Feb 12 2018) 81 Porsche Race Career High Doubles Rank 95 (Jul 27 2015) To Singapore WTA Singles Titles - YTD / Career 0 / 0 POL WTA Doubles Titles - YTD / Career 0 / 0 PERFORMANCE - SINGLES* *Stats include active tournament results STATS MD YTD (2018) MD CAREER ALL YTD (2018) ALL CAREER Tournament (WASHINGTON DC) W - L 1- - 0 01 - 1 1- - 0 01 - 1 Grand Slam W - L 2 - 3 5 - 14 2 - 3 7 - 24 Overall W - L 11 - 14 53 - 72 17 - 19 307 - 227 3 Set W - L 4 - 6 19 - 26 7 - 9 88 - 94 1 Set W - L 10 - 4 39 - 11 15 - 5 255 - 52 Tie Break W - L 2 - 4 16 - 11 4 - 6 55 - 68 Surface (HARD) W - L 9 - 7 42 - 49 10 - 8 165 - 116 Surface (CLAY) W - L 2 - 5 9 - 13 6 - 8 120 - 84 Surface (GRASS) W - L 0 - 2 2 - 10 1 - 3 11 - 20 Top 5 W - L 0 - 0 0 - 3 0 - 0 0 - 3 Top 10 W - L 0 - 0 0 - 6 0 - 0 0 - 6 Top 20 W - L 0 - 0 0 - 15 0 - 0 0 - 15 Top 100 W - L 3 - 9 25 - 54 3 - 9 39 - 81 vs. -

Dr. Alejandro Badia……………………………….3
Alejandro Badia, MD, FACS Hand & Upper Extremity Surgeon Table of Contents About Dr. Alejandro Badia……………………………….3 Awards & Recognitions………………………………..4-5 Speaking Engagements………………………………...6-9 Research & Clinical Articles.…………………………...10 Dr. Badia in the News……………………………….11-12 Badia Hand to Shoulder Center………………………..13 OrthoNOW® Orthopedic Urgent Care Center….….…....14 Celebrity Patients……………………………………….15 Patient Testimonials…………………………………….16 Medical Missions……………………………………….17 Topics…………………………………………………...18 2 About Dr. Alejandro Badia Alejandro Badia, MD, FACS is an internationally respected hand and upper extremity surgeon and the CEO of Badia Hand to Shoulder Center in Doral, Florida. Dr. Badia graduated from Cornell University and completed his medical degree at NYU. He served as the worldwide president of ISSPORTH and co-founded the globally recognized Miami Anatomical Research and Training Center (M.A.R.C.) and The Surgery Center at Doral, an elite state-of-the-art ambulatory surgery center. In 2014, his frustration with the health care system sparked the idea for the creation of specialized orthopedic urgent care centers to efficiently assess and treat a range of orthopedic and sports injuries. To that end, he founded OrthoNOW®, the only network of franchised orthopedic urgent care centers in the country with 42 centers slated to open coast to coast in the next five years. , He has revolutionized the delivery of healthcare to patients resulting in better outcomes, less wait times and decreased cost of care. Dr. Badia, comes from a family of physicians and is a descendant of the founder of the Cuban Academy of Sciences, who was motivated to become a surgeon to help care for people like his grandmother who suffered chronic pain from advanced arthritis with crippling deformities. -

2020 Western & Southern Open Doubles Field
Western & Southern Open Defending Champions Headline Doubles Fields CINCINNATI (Aug. 11, 2020) – Both the women’s and men’s defending champions are among the initial entries to play doubles at the 2020 Western & Southern Open, which will be held Aug. 20-28 at the USTA Billie Jean King Tennis Center in New York. The 2019 WTA doubles winners – Lucie Hradecka and Andreja Klepac – are joined by the ATP Tour champions – Ivan Dodig and Filip Polasek – to headline the early entries. Other notable entries on the women’s side include the teenage pairing of Cincinnati’s 18-year-old Caty McNally and 16-year-old Coco Gauff. Dubbed “McCoco,” the duo won a pair of WTA titles in 2019 – at Washington, D.C. and Luxembourg – and reached the US Open Round of 16. Elise Mertens and Aryna Sabalenka, who finished 2019 atop the WTA Porsche Race to Shenzen as the season’s No. 1 team, are also in the field. Reigning Australian Open singles champion Sofia Kenin, a 21-year- old American, has entered with former Western & Southern Open singles and doubles winner Victoria Azarenka. The top two teams in the ATP Tour doubles race are entered in the men’s draw. The No. 1 team of Juan Sebastian Cabal and Robert Farah is returning after reaching two straight Western & Southern Open finals. They are joined in the field by the No. 2 team of Lukasz Kubot and Marcelo Melo. The ATP Tour No. 1 ranked singles player, Novak Djokovic, has entered the doubles draw with countryman Filip Krajinovic. An additional five women’s teams and six men’s duos will join the fields through on-site entries, while the tournament will award three wild cards into each draw to complete the 32-team fields. -
Iowa City, Iowa - Wednesday, September 2, 2009 News Dailyiowan.Com for More News
WEDNESDAY, SEPTEMBER 2, 2009 SPORTS No Go Bejeweled no more Zone Iowa head coach Kirk Ferentz reveals that sophomore run- ning back Jewel Hampton is Some food vendors out for the season with a leg injury. 12 are cautious Iron ridge about delivering The Iowa men’s golf team takes to the city’s second at the Golfweek Conference Challenge on Tuesday. 12 Southeast Side. By DANNY VALENTINE NEWS [email protected] Rushin’ to take One local business will no Russian longer deliver pizzas to the city’s Southeast Side after An increasing number of UI JOE SCOTT/THE DAILY IOWAN two of its employees were students are opting to take Yellow Cab driver Roman Schoenberger heads up Burlington Street on Tuesday on his way to a fare. Yellow Cab is the only company in recently robbed at gunpoint. classes in Russian. 2 town that accepts Cab Cash, a debit-style card that people can use for rides home. The decision came after a Meet the third armed robbery on Monday night, which even- candidates tually resulted in the arrest Read what the six Iowa City of three men who are School Board candidates have Iowa City hails cab card allegedly connected to the to say about district issues. 2 two pizza-delivery incidents University Cab Cash and one other case. ARTS & CULTURE The days of students standing on the curb, Reginald Payne, 20, The program cites drunk driving as an Laron James, 19, both of More typical ethnic wishing for money for a cab, are over. incentive for using its service. -

Volvo Car Open ORDER of PLAY - TUESDAY, 3 APRIL 2018
Volvo Car Open ORDER OF PLAY - TUESDAY, 3 APRIL 2018 VOLVO CAR STADIUM ALTHEA GIBSON CLUB COURT COURT 3 COURT 4 Starting at: 10:00 am Starting at: 10:00 am Starting at: 10:00 am Starting at: 11:00 am Sofia KENIN (USA) Heather WATSON (GBR) [Q] Claire LIU (USA) 1 vs vs vs Ashleigh BARTY (AUS) [9] Taylor TOWNSEND (USA) Magda LINETTE (POL) followed by followed by followed by Starting at: 11:00 am Kristie AHN (USA) Elena VESNINA (RUS) [16] Irina-Camelia BEGU (ROU) [13] Beatriz HADDAD MAIA (BRA) 2 vs vs vs vs Samantha STOSUR (AUS) Madison BRENGLE (USA) [Q] Georgina GARCIA PEREZ (ESP) Lara ARRUABARRENA (ESP) followed by followed by followed by followed by Nicole MELICHAR (USA) Monique ADAMCZAK (AUS) Eugenie BOUCHARD (CAN) Lauren DAVIS (USA) Kveta PESCHKE (CZE) Lyudmyla KICHENOK (UKR) 3 vs vs vs vs [WC] Sara ERRANI (ITA) Tatjana MARIA (GER) Alla KUDRYAVTSEVA (RUS) Nadiia KICHENOK (UKR) Katarina SREBOTNIK (SLO) Anastasia RODIONOVA (AUS) followed by followed by followed by Shuko AOYAMA (JPN) Caroline GARCIA (FRA) [1] Katerina SINIAKOVA (CZE) Zhaoxuan YANG (CHN) 4 vs vs vs Varvara LEPCHENKO (USA) Kristyna PLISKOVA (CZE) Bethanie MATTEK-SANDS (USA) Andrea SESTINI HLAVACKOVA (CZE) [2] Not Before 7:00 pm Christina MCHALE (USA) 5 vs Daria KASATKINA (RUS) [3] followed by Gabriela DABROWSKI (CAN) Yifan XU (CHN) [1] 6 vs Raquel ATAWO (USA) Anna-Lena GROENEFELD (GER) Bob Moran Brad Taylor Pam Whytcross Tournament Director Referee WTA Supervisor Order of Play released : 2 April 2018 at 17:53 Singles Lucky-Losers Sign-in Deadline : 9:30 AM MATCHES WILL BE CALLED BY ANY MATCH ON ANY COURT Doubles Alternates Sign-in Deadline : 11:30 AM THE REFEREE MAY BE MOVED CHECK FOR MEETING POINT www.wtatennis.com | facebook.com/WTA | twitter.com/WTA | youtube.com/WTA. -
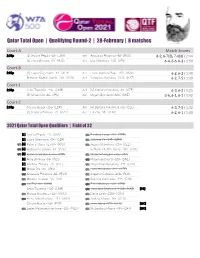
Announcer Andy Taylor. 2021 Qatar Total Open. Qualifying Round-2
Qatar Total Open | Qualifying Round-2 | 28-February | 8 matches Court-A Match Scores 2:30p [1] Jessica Pegula -43- (USA) def Anastasia Potapova -88- (RUS) 6-2, 6-7(3), 7-6(6) / 2:44 [6] Anna Blinkova -69- (RUS) def Ena Shibahara -502- (JPN) 6-4, 3-6, 6-2 / 1:50 Court-B 2:30p [2] Laura Siegemund -54- (GER) def Elena-Gabriela Ruse -164- (ROU) 6-2, 6-2 / 1:40 Bethanie Mattek-Sands -299- (USA) def Yaroslava Shvedova -1028- (KAZ) 6-2, 7-5 / 1:30 Court-1 2:30p Lesia Tsurenko -145- (UKR) def [5] Katerina Siniakova -68- (CZE) 6-3, 6-2 / 1:25 [8] Misaki Doi -86- (JPN) def Mirjam Bjorklund -320- (SWE) 3-6, 6-1, 6-1 / 1:42 Court-2 2:30p Cristina Bucsa -166- (ESP) def [4] Barbora Krejcikova -63- (CZE) 6-3, 7-5 / 1:32 [7] Kristyna Pliskova -75- (CZE) def Lin Zhu -98- (CHN) 6-2, 6-1 / 1:00 2021 Qatar Total Open Qualifiers | Field of 32 [1] Jessica Pegula -43- (USA) QR1 En-shuo Liang -237- (TPE) [2] Laura Siegemund -54- (GER) QR1 Gabriela Ce -247- (BRA) QR1 [3] Patricia Maria Tig -60- (ROU) QR1 Jessica Maleckova -297- (CZE) QR2 [4] Barbora Krejcikova -63- (CZE) Bethanie Mattek-Sands -299- (USA) QR2 [5] Katerina Siniakova -68- (CZE) QR1 Martina Caregaro -300- (ITA) [6] Anna Blinkova -69- (RUS) QR2 Mirjam Bjorklund -320- (SWE) [7] Kristyna Pliskova -75- (CZE) QR1 Akgul Amanmuradova -425- (UZB) [8] Misaki Doi -86- (JPN) QR1 Lucie Hradecka -427- (CZE) QR2 Anastasia Potapova -88- (RUS) QR1 Angelina Gabueva -468- (RUS) QR1 Martina Trevisan -90- (ITA) QR1 Gabriela Dabrowski -495- (CAN) QR2 Lin Zhu -98- (CHN) QR2 Ena Shibahara -502- (JPN) Lesia Tsurenko -145- (UKR) QR2 Yaroslava Shvedova -1028- (KAZ) [PR] QR1 Monica Niculescu -147- (ROU) QR1 Darija Jurak -1260- (CRO) QR2 Elena-Gabriela Ruse -164- (ROU) QR1 Andreja Klepac -NR- (SLO) Cristina Busca -166- (ESP) QR1 Innes Ibbou -571- (ALG) [WC] QR1 Lesley Pattinama Kerkhove -181- (NED) QR1 Mubaraka al-Naimi -NR- (QAT) [WC] Qatar Total Open 2021 CITY, COUNTRY TOURNAMENT DATES SURFACE ON-SITE PRIZE MONEY DOHA, QAT March 1-6, 2021 Hard $ 565,530 STATUS NAT QUALIFYING SINGLES 1 1 PEGULA, Jessica USA J. -

2020 Women’S Tennis Association Media Guide
2020 Women’s Tennis Association Media Guide © Copyright WTA 2020 All Rights Reserved. No portion of this book may be reproduced - electronically, mechanically or by any other means, including photocopying- without the written permission of the Women’s Tennis Association (WTA). Compiled by the Women’s Tennis Association (WTA) Communications Department WTA CEO: Steve Simon Editor-in-Chief: Kevin Fischer Assistant Editors: Chase Altieri, Amy Binder, Jessica Culbreath, Ellie Emerson, Katie Gardner, Estelle LaPorte, Adam Lincoln, Alex Prior, Teyva Sammet, Catherine Sneddon, Bryan Shapiro, Chris Whitmore, Yanyan Xu Cover Design: Henrique Ruiz, Tim Smith, Michael Taylor, Allison Biggs Graphic Design: Provations Group, Nicholasville, KY, USA Contributors: Mike Anders, Danny Champagne, Evan Charles, Crystal Christian, Grace Dowling, Sophia Eden, Ellie Emerson,Kelly Frey, Anne Hartman, Jill Hausler, Pete Holtermann, Ashley Keber, Peachy Kellmeyer, Christopher Kronk, Courtney McBride, Courtney Nguyen, Joan Pennello, Neil Robinson, Kathleen Stroia Photography: Getty Images (AFP, Bongarts), Action Images, GEPA Pictures, Ron Angle, Michael Baz, Matt May, Pascal Ratthe, Art Seitz, Chris Smith, Red Photographic, adidas, WTA WTA Corporate Headquarters 100 Second Avenue South Suite 1100-S St. Petersburg, FL 33701 +1.727.895.5000 2 Table of Contents GENERAL INFORMATION Women’s Tennis Association Story . 4-5 WTA Organizational Structure . 6 Steve Simon - WTA CEO & Chairman . 7 WTA Executive Team & Senior Management . 8 WTA Media Information . 9 WTA Personnel . 10-11 WTA Player Development . 12-13 WTA Coach Initiatives . 14 CALENDAR & TOURNAMENTS 2020 WTA Calendar . 16-17 WTA Premier Mandatory Profiles . 18 WTA Premier 5 Profiles . 19 WTA Finals & WTA Elite Trophy . 20 WTA Premier Events . 22-23 WTA International Events . -

2020 Us Open Singles Prize Money & Ranking Points
2020 US OPEN – WOMEN’S PREVIEW NOTES NEW YORK, NY, USA – AUG 31-SEPT 13, 2020 – GRAND SLAM Tournament Information: www.usopen.org | @usopen | facebook.com/usopentennis WTA Information: www.wtatennis.com | @WTA | facebook.com/WTA WTA Communications: Estelle La Porte ([email protected]), Bryan Shapiro ([email protected]), Chase Altieri ([email protected]), Teyva Sammet ([email protected]) 2020 US OPEN First held in 1887, the US Open women’s singles championship is being staged for the 134th time. The 2020 event marks the 53rd staging of the Open Era, which began in 1968 and saw the introduction of prize money. Overall this is the 140th US Open, the men’s event having first being held in 1881. Here is a breakdown of the rewards on offer in 2020: SINGLES PRIZE MONEY & RANKING POINTS PRIZE RANKING ROUND MONEY (US$) POINTS Winner 3,000,000 2000 Runner-Up 1,500,000 1300 Semifinalists 800,000 780 Quarterfinalists 425,000 430 Round of 16 (4r) 250,000 240 Round of 32 (3r) 163,000 130 Round of 64 (2r) 100,000 70 Round of 128 (1r) 61,000 10 SEEDED FOR FIRST TIME AT A SLAM Magda Linette (POL) – No.24 (21st Grand Slam MD appearance) Ons Jabeur (TUN) – No.27 (14th Grand Slam MD appearance) Jennifer Brady (USA) – No.28 (13th Grand Slam MD appearance) Veronika Kudermetova (RUS) – No.29 (sixth Grand Slam MD appearance) Rebecca Peterson (SWE) – No.32 (10th Grand Slam MD appearance) WTA SPECIAL RANKINGS The following players are using a Special Ranking to gain entry into this year’s US Open: Kateryna Bondarenko (UKR) – No.85 Irina Khromacheva (RUS) – No.137 Vera Lapko (BLR) – No.120 Tsvetana Pironkova (BUL) – No.123 Vera Zvonareva (RUS) – No.78 Follow WTA on Twitter: www.twitter.com/WTA Facebook: www.facebook.com/WTA YouTube Channel: www.youtube.com/WTA 1 2020 US OPEN – WOMEN’S PREVIEW NOTES NEW YORK, NY, USA – AUG 31-SEPT 13, 2020 – GRAND SLAM ACTIVE GRAND SLAM CHAMPIONS The 2020 season has already welcomed one new Grand Slam champion: Sofia Kenin won her maiden Grand Slam singles title at Melbourne Park in January, defeating Garbiñe Muguruza in the final. -

Us Open August 31 – September 13, 2020 Women’S Tennis Association Match Notes
US OPEN AUGUST 31 – SEPTEMBER 13, 2020 WOMEN’S TENNIS ASSOCIATION MATCH NOTES FLUSHING MEADOWS, NEW YORK | AUGUST 31 - SEPTEMBER 13, 2020 | $21,656,000 GRAND SLAM TOURNAMENT wtatennis.com | facebook.com/WTA | twitter.com/WTA | youtube.com/WTA Tournament Website: www.wimbledon.com | @Wimbledon | facebook.com/wimbledon WTA Communications: Estelle LaPorte, Chase Altieri, Teyva Sammet US OPEN - DAY 1 MATCH-UPS [1] KAROLINA PLISKOVA (CZE #3) vs. ANHELINA KALININA (UKR #145) First meeting Pliskova seeded No.1 for the second time in her career at a major... Kalinina bidding for first Top 20 win of career... Pliskova’s runner-up finish here in 2016 remains best major result [4] NAOMI OSAKA (JPN #9) vs. MISAKI DOI (JPN #81) Osaka leads 1-0 Osaka beat her compatriot en route to Tokyo final in 2016...Doi has never overcome a Top 10 player in her career... Osaka is one of six former US Open champions in the draw IRINA CAMELIA BEGU (ROU #73) vs. [6] PETRA KVITOVA (CZE #12) Kvitova leads 4-0 Kvitova beat Begu during title runs at 2018 St. Petersburg and 2015 Madrid... Begu has not upset a Top 20 player since 2018 clay court season... US Open is only major where Kvitova has failed to reach SF TEREZA MARTINCOVA (CZE #136) vs. [8] PETRA MARTIC (CRO #15) First meeting (at main draw, tour level) Martic won when the two met in qualifying at 2015 Bad Gastein... Martincova is lowest-ranked of eight Czechs in the draw... Martic lost to Williams in R16 here last year TATJANA MARIA (GER #95) vs. -

Connecticut Open Presented by United Technologies
Connecticut Open presented by United Technologies ORDER OF PLAY - FRIDAY, 15 AUGUST 2014 GRANDSTAND COURT 1 COURT 2 COURT 3 COURT C COURT A COURT G COURT I Starting at: 10:00 am Starting at: 10:00 am Starting at: 10:00 am Starting at: 10:00 am Starting at: 10:00 am Starting at: 10:00 am Starting at: 10:00 am Starting at: 10:00 am WTA WTA WTA WTA WTA WTA OTH OTH Varvara LEPCHENKO (USA) Donna VEKIC (CRO) Sílvia SOLER-ESPINOSA (ESP) Jana CEPELOVA (SVK) [WC] An-Sophie MESTACH (BEL) Mona BARTHEL (GER) [Alt] Nicole MELICHAR (USA) Jennifer ELIE (USA) [3] 1 vs vs vs vs vs vs vs vs Aleksandra WOZNIAK (CAN) Belinda BENCIC (SUI) Claire FEUERSTEIN (FRA) Anna-Lena FRIEDSAM (GER) Julia GLUSHKO (ISR) Kiki BERTENS (NED) Michaela GORDON (USA) Jessie ANEY (USA) followed by followed by followed by followed by followed by followed by followed by followed by WTA WTA WTA WTA WTA WTA OTH OTH Lauren DAVIS (USA) Olga GOVORTSOVA (BLR) [WC] Caitlin WHORISKEY (USA) Karolina PLISKOVA (CZE) Alison VAN UYTVANCK (BEL) Irina-Camelia BEGU (ROU) Skylar MORTON (USA) [Alt] Petra JANUSKOVA (CAN) 2 vs vs vs vs vs vs vs vs Timea BACSINSZKY (SUI) Grace MIN (USA) Pauline PARMENTIER (FRA) Monica NICULESCU (ROU) [WC] Sorana CIRSTEA (ROU) Zarina DIYAS (KAZ) Julie DITTY (USA) Ashley WEINHOLD (USA) [4] followed by followed by followed by followed by followed by followed by followed by followed by WTA WTA WTA WTA WTA WTA OTH OTH Francesca SCHIAVONE (ITA) Shahar PEER (ISR) Johanna KONTA (GBR) Annika BECK (GER) Polona HERCOG (SLO) Karin KNAPP (ITA) Jacqueline CAKO (USA) [5] [Alt] Zoe -

Tournament Champion
1/15/2019 2019 AusOpen 2019 - Women's Doubles 1st Round 2nd Round 3rd Round Quarterfinals Semifinals TOURNAMENT CHAMPION Barbora Krejcikova (CZE)(1) - 1 - Katerina Siniakova (CZE)(1) - Ana Bogdan (ROU) 2 - Anastasia Rodionova (AUS) - - - - Aleksandra Krunic (SRB) 3 Saisai Zheng (CHN) Monique Adamczak (AUS) 4 Jessica Moore (AUS) - - - - Veronika Kudermetova (RUS) 5 Sabrina Santamaria (USA) Belinda Bencic (SUI) 6 Donna Vekic (CRO) - - - - Elise Mertens (BEL) 7 Aryna Sabalenka (BLR) Bethanie Mattek-Sands (USA)(15) 8 Demi Schuurs (NED)(15) - - - - Irina-Camelia Begu (ROU)(10) 9 Mihaela Buzarnescu (ROU)(10) Lizette Cabrera (AUS)(WC) 10 Jaimee Fourlis (AUS)(WC) - - - - Alizé Cornet (FRA) 11 Petra Martic (CRO) Magda Linette (POL) 12 Ajla Tomljanovic (AUS) - - - - Viktoria Kuzmova (SVK) 13 Magdalena Rybarikova (SVK) Samantha Stosur (AUS) 14 Shuai Zhang (CHN) - - - - Bernarda Pera (USA) 15 Rebecca Peterson (SWE) Su-Wei Hsieh (TPE)(8) 16 Abigail Spears (USA)(8) - TOURNAMENT - SEEDS - - (1) B. Krejcikova Gabriela Dabrowski (CAN)(3) 17 K. Siniakova Yifan Xu (CHN)(3) Barbora Strycova (CZE) (2) T. Babos 18 Marketa Vondrousova (CZE) - K. Mladenovic - (3) G. Dabrowski - - Y. Xu Dalila Jakupovic (SLO) 19 (4) N. Melichar Irina Khromacheva (RUS) K. Peschke Zarina Diyas (KAZ) 20 Yulia Putintseva (KAZ) (5) A. Klepac - - M. Martinez Sanchez - (6) L. Hradecka - Luksika Kumkhum (THA)(A) E. Makarova 21 Evgeniya Rodina (RUS)(A) (7) H. Chan Alison Bai (AUS)(WC) 22 Zoe Hives (AUS)(WC) L. Chan - - (8) S. Hsieh - A. Spears - Nao Hibino (JPN) (9) R. Atawo 23 Desirae Krawczyk (USA) K. Srebotnik Miyu Kato (JPN)(14) 24 (10) I. Begu Makoto Ninomiya (JPN)(14) - M. -
QUEEN of the DIAMOND KIMBERLY’S MAKINGS IS 2009 SOFTBALL ATHLETE of the YEAR Sunny and Hot
90 / 59 QUEEN OF THE DIAMOND KIMBERLY’S MAKINGS IS 2009 SOFTBALL ATHLETE OF THE YEAR Sunny and hot. SPORTS 1 Business 6 RURAL UNEMPLOYMENT >>> Economists say rural communities doing better than reports suggest, BUSINESS 1 FRIDAY 75 CENTS May 29, 2009 MagicValley.com Police: vulnerable patient abused by sex offender court. “They also had offer a release today. St. Luke’s Canyon View slow to report alleged assault to police knowledge that Mr. Knutsen Idaho Department of is a sex offender. Apparently, Health and Welfare authori- By Andrea Jackson for six days after Canyon the alleged victim was a 21- supervision when the sexual their only mediation in ties on Thursday would not Times-News writer View officials learned of it, year-old female patient at abuse occurred, according to regards to keeping (her) and say if they knew about the according to 5th District Canyon View. court records. Mr. Knutsen from having allegations involving Can- A patient at St. Luke’s Court records. He was supposed to enter “I also relayed the concern contact with one another yon View. Spokeswoman Canyon View Behavioral Registered sex offender a plea earlier this week, but that I had that the Canyon was to check on them every Emily Simnitt cited patient Health Services claimed she David Aaron Knutsen, 28, of that was postponed until View staff knew that (vic- 15 minutes.” confidentiality and the was sexually abused in Filer, was indicted March 25 June 22. tim) is a vulnerable adult Officials with the hospital Health Insurance Portability January by a registered sex on four counts of sexual Knutsen and the develop- from the minute she was declined comment Thurs- and Accountability Act.