DOCSLIB.ORG

I. Sorting Networks Thomas Sauerwald

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
I. Sorting Networks Thomas Sauerwald I. Sorting Networks Thomas Sauerwald Easter 2015 Outline Introduction to Sorting Networks Batcher’s Sorting Network Counting Networks Load Balancing on Graphs I. Sorting Networks Introduction to Sorting Networks 2 Overview: Sorting Networks (Serial) Sorting Algorithms we already know several (comparison-based) sorting algorithms: Insertion sort, Bubble sort, Merge sort, Quick sort, Heap sort execute one operation at a time can handle arbitrarily large inputs sequence of comparisons is not set in advance Sorting Networks only perform comparisons can only handle inputs of a fixed size sequence of comparisons is set in advance Allows to sort n numbers Comparisons can be performed in parallel in sublinear time! Simple concept, but surprisingly deep and complex theory! I. Sorting Networks Introduction to Sorting Networks 3 Comparison Networks A sorting network is a comparison network which Comparison Network works correctly (that is, it sorts every input) A comparison network consists solely of wires and comparators: comparator is a device with, on given two inputs, x and y, returns two operates in O(1) outputs x0 and y 0 wire connect output of one comparator to the input of another special wires: n input wires a1; a2;:::; an and n output wires b1; b2;:::; bn Convention:27.1 Comparison use networks the same name for both a wire and its value. 705 7 3 x x! min(x, y) x x ! min(x, y) comparator = = 3 7 y y! max(x, y) y y! max(x, y) = = (a) (b) Figure 27.1 (a) Acomparatorwithinputsx and y and outputs x! and y!. (b) The same comparator, drawn as a single vertical line. Inputs x 7, y 3andoutputsx 3, y 7areshown. = = ! = ! = Acomparisonnetworkiscomposedsolelyofwiresandcomparators. A compara- tor,showninFigure27.1(a),isadevicewithtwoinputs,I. Sorting Networks Introduction to Sorting Networks x and y,andtwooutputs,4 x! and y!,thatperformsthefollowingfunction: x! min(x, y), = y! max(x, y). = Because the pictorial representation of a comparator in Figure 27.1(a) is too bulky for our purposes, we shall adopt the convention of drawing comparators as single vertical lines, as shown in Figure 27.1(b). Inputs appear on the left and outputs on the right, with the smaller input value appearing on the top output and the larger input value appearing on the bottom output. We can thus think of a comparator as sorting its two inputs. We shall assume that each comparator operates in O(1) time. In other words, we assume that the time between the appearance of the input values x and y and the production of the output values x! and y! is a constant. A wire transmits a value from place to place. Wires can connect the output of one comparator to the input of another, but otherwise they are either network input wires or network output wires. Throughout this chapter, we shall assume that a comparison network contains n input wires a1, a2,...,an,throughwhich the values to be sorted enter the network, and n output wires b1, b2,...,bn,which produce the results computed by the network. Also, we shall speak of the input sequence a1, a2,...,an and the output sequence b1, b2,...,bn ,referringto the values" on the input and# output wires. That is, we use" the same name# for both a wire and the value it carries. Our intention will always be clear from the context. Figure 27.2 shows a comparison network,whichisasetofcomparatorsinter- connected by wires. We draw a comparison network on n inputs as a collection of n horizontal lines with comparators stretched vertically. Note that a line does not represent a single wire, but rather a sequence of distinct wires connecting vari- ous comparators. The top line in Figure 27.2, for example, represents three wires: input wire a1,whichconnectstoaninputofcomparatorA;awireconnectingthe top output of comparator A to an input of comparator C;andoutputwireb1,which comes from the top output of comparator C.Eachcomparatorinputisconnected X Interconnections between comparators must be acyclic 9 5 2 2 5 9 6 5 F D F 2 2 F 5 6 D 6 6 9 9 depth 0 1 1 2 2 3 TracingThis backnetwork a path is in must fact a neverMaximum sorting cycle network! depth back ofon an output Depth of a wire: itself and go through the samewire comparator equals total twice. running time Input wire has Depth 0 If a comparator has two inputs of depths dx and dy , then outputs have depth maxfdx ; dy g + 1 Example of a Comparison Network (Figure 27.2) A horizontal line represents a sequence of distinct wires a1 b1 A C a2 b2 E a3 b3 B D a4 b4 I. Sorting Networks Introduction to Sorting Networks 5 A horizontal line represents a sequence of distinctX wires 9 5 2 2 5 9 6 5 D F 2 2 F 5 6 D 6 6 9 9 depth 0 1 1 2 2 3 TracingThis backnetwork a path is in must fact a neverMaximum sorting cycle network! depth back ofon an output Depth of a wire: itself and go through the samewire comparator equals total twice. running time Input wire has Depth 0 If a comparator has two inputs of depths dx and dy , then outputs have depth maxfdx ; dy g + 1 Example of a Comparison Network (Figure 27.2) Interconnections between comparators must be acyclic a1 b1 A C a2 b2 F E a3 b3 B D a4 b4 I. Sorting Networks Introduction to Sorting Networks 5 A horizontal line represents a sequence of distinct wires 9 5 2 2 5 9 6 5 F D 2 2 F 5 6 D 6 6 9 9 depth 0 1 1 2 2 3 TracingThis backnetwork a path is in must fact a neverMaximum sorting cycle network! depth back ofon an output Depth of a wire: itself and go through the samewire comparator equals total twice. running time Input wire has Depth 0 If a comparator has two inputs of depths dx and dy , then outputs have depth maxfdx ; dy g + 1 Example of a Comparison Network (Figure 27.2) Interconnections between comparators must be acyclic X a1 b1 A C a2 b2 D F E a3 b3 B a4 b4 I. Sorting Networks Introduction to Sorting Networks 5 A horizontal line represents a sequence of distinctX wires 9 5 2 2 5 9 6 5 F D F 2 2 5 6 D 6 6 9 9 depth 0 1 1 2 2 3 This network is in fact aMaximum sorting network! depth of an output Depth of a wire: wire equals total running time Input wire has Depth 0 If a comparator has two inputs of depths dx and dy , then outputs have depth maxfdx ; dy g + 1 Example of a Comparison Network (Figure 27.2) Interconnections between comparators must be acyclic a1 b1 A C a2 b2 E F a3 b3 B D a4 b4 Tracing back a path must never cycle back on itself and go through the same comparator twice. I. Sorting Networks Introduction to Sorting Networks 5 X InterconnectionsA horizontal between line represents comparators a sequencemust be of acyclic distinct wires F D F F D depth 0 1 1 2 2 3 Tracing back a path must neverMaximum cycle depth back ofon an output Depth of a wire: itself and go through the samewire comparator equals total twice. running time Input wire has Depth 0 If a comparator has two inputs of depths dx and dy , then outputs have depth maxfdx ; dy g + 1 Example of a Comparison Network (Figure 27.2) 9 5 2 2 a1 b1 A C 5 9 6 5 a2 b2 E 2 2 5 6 a3 b3 B D 6 6 9 9 a4 b4 This network is in fact a sorting network! I. Sorting Networks Introduction to Sorting Networks 5 X InterconnectionsA horizontal between line represents comparators a sequencemust be of acyclic distinct wires F D F F D TracingThis backnetwork a path is in must fact a never sorting cycle network! back on itself and go through the same comparator twice. Example of a Comparison Network (Figure 27.2) 9 5 2 2 a1 b1 A C 5 9 6 5 a2 b2 E 2 2 5 6 a3 b3 B D 6 6 9 9 a4 b4 depth 0 1 1 2 2 3 Maximum depth of an output Depth of a wire: wire equals total running time Input wire has Depth 0 If a comparator has two inputs of depths dx and dy , then outputs have depth maxfdx ; dy g + 1 I. Sorting Networks Introduction to Sorting Networks 5 Zero-One Principle Zero-One Principle: A sorting networks works correctly on arbitrary in- puts if it works correctly on binary inputs. Lemma 27.1 If a comparison network transforms the input a = ha1; a2;:::; ani into the output b = hb1; b2;:::; bni, then for any monotonically increasing function f , the network transforms f (a) = hf (a1); f (a2);:::; f (an)i into f (b) = hf (b1); f (b2);:::; f (bn)i. 710 Chapter 27 Sorting Networks f (x) min( f (x), f (y)) f (min(x, y)) = f (y) max( f (x), f (y)) f (max(x, y)) = Figure 27.4 The operation of the comparator in the proof of Lemma 27.1. Thefunction f is monotonically increasing. To prove the claim, consider a comparator whose input values are x and y.The upper output of the comparator is min(x, y) and the lower output is max(x, y). I. Sorting Networks Introduction to Sorting Networks 6 Suppose we now apply f (x) and f (y) to the inputs of the comparator, as is shown in Figure 27.4.
Load more

Recommended publications
  • Sort Algorithms 15-110 - Friday 2/28 Learning Objectives
    Sort Algorithms 15-110 - Friday 2/28 Learning Objectives • Recognize how different sorting algorithms implement the same process with different algorithms • Recognize the general algorithm and trace code for three algorithms: selection sort, insertion sort, and merge sort • Compute the Big-O runtimes of selection sort, insertion sort, and merge sort 2 Search Algorithms Benefit from Sorting We use search algorithms a lot in computer science. Just think of how many times a day you use Google, or search for a file on your computer. We've determined that search algorithms work better when the items they search over are sorted. Can we write an algorithm to sort items efficiently? Note: Python already has built-in sorting functions (sorted(lst) is non-destructive, lst.sort() is destructive). This lecture is about a few different algorithmic approaches for sorting. 3 Many Ways of Sorting There are a ton of algorithms that we can use to sort a list. We'll use https://visualgo.net/bn/sorting to visualize some of these algorithms. Today, we'll specifically discuss three different sorting algorithms: selection sort, insertion sort, and merge sort. All three do the same action (sorting), but use different algorithms to accomplish it. 4 Selection Sort 5 Selection Sort Sorts From Smallest to Largest The core idea of selection sort is that you sort from smallest to largest. 1. Start with none of the list sorted 2. Repeat the following steps until the whole list is sorted: a) Search the unsorted part of the list to find the smallest element b) Swap the found element with the first unsorted element c) Increment the size of the 'sorted' part of the list by one Note: for selection sort, swapping the element currently in the front position with the smallest element is faster than sliding all of the numbers down in the list.
    [Show full text]
  • CS 758/858: Algorithms
    CS 758/858: Algorithms ■ COVID Prof. Wheeler Ruml Algorithms TA Sumanta Kashyapi This Class Complexity http://www.cs.unh.edu/~ruml/cs758 4 handouts: course info, schedule, slides, asst 1 2 online handouts: programming tips, formulas 1 physical sign-up sheet/laptop (for grades, piazza) Wheeler Ruml (UNH) Class 1, CS 758 – 1 / 25 COVID ■ COVID Algorithms This Class Complexity ■ check your Wildcat Pass before coming to campus ■ if you have concerns, let me know Wheeler Ruml (UNH) Class 1, CS 758 – 2 / 25 ■ COVID Algorithms ■ Algorithms Today ■ Definition ■ Why? ■ The Word ■ The Founder This Class Complexity Algorithms Wheeler Ruml (UNH) Class 1, CS 758 – 3 / 25 Algorithms Today ■ ■ COVID web: search, caching, crypto Algorithms ■ networking: routing, synchronization, failover ■ Algorithms Today ■ machine learning: data mining, recommendation, prediction ■ Definition ■ Why? ■ bioinformatics: alignment, matching, clustering ■ The Word ■ ■ The Founder hardware: design, simulation, verification ■ This Class business: allocation, planning, scheduling Complexity ■ AI: robotics, games Wheeler Ruml (UNH) Class 1, CS 758 – 4 / 25 Definition ■ COVID Algorithm Algorithms ■ precisely defined ■ Algorithms Today ■ Definition ■ mechanical steps ■ Why? ■ ■ The Word terminates ■ The Founder ■ input and related output This Class Complexity What might we want to know about it? Wheeler Ruml (UNH) Class 1, CS 758 – 5 / 25 Why? ■ ■ COVID Computer scientist 6= programmer Algorithms ◆ ■ Algorithms Today understand program behavior ■ Definition ◆ have confidence in results, performance ■ Why? ■ The Word ◆ know when optimality is abandoned ■ The Founder ◆ solve ‘impossible’ problems This Class ◆ sets you apart (eg, Amazon.com) Complexity ■ CPUs aren’t getting faster ■ Devices are getting smaller ■ Software is the differentiator ■ ‘Software is eating the world’ — Marc Andreessen, 2011 ■ Everything is computation Wheeler Ruml (UNH) Class 1, CS 758 – 6 / 25 The Word: Ab¯u‘Abdall¯ah Muh.ammad ibn M¯us¯aal-Khw¯arizm¯ı ■ COVID 780-850 AD Algorithms Born in Uzbekistan, ■ Algorithms Today worked in Baghdad.
    [Show full text]
  • Improving the Performance of Bubble Sort Using a Modified Diminishing Increment Sorting
    Scientific Research and Essay Vol. 4 (8), pp. 740-744, August, 2009 Available online at http://www.academicjournals.org/SRE ISSN 1992-2248 © 2009 Academic Journals Full Length Research Paper Improving the performance of bubble sort using a modified diminishing increment sorting Oyelami Olufemi Moses Department of Computer and Information Sciences, Covenant University, P. M. B. 1023, Ota, Ogun State, Nigeria. E- mail: [email protected] or [email protected]. Tel.: +234-8055344658. Accepted 17 February, 2009 Sorting involves rearranging information into either ascending or descending order. There are many sorting algorithms, among which is Bubble Sort. Bubble Sort is not known to be a very good sorting algorithm because it is beset with redundant comparisons. However, efforts have been made to improve the performance of the algorithm. With Bidirectional Bubble Sort, the average number of comparisons is slightly reduced and Batcher’s Sort similar to Shellsort also performs significantly better than Bidirectional Bubble Sort by carrying out comparisons in a novel way so that no propagation of exchanges is necessary. Bitonic Sort was also presented by Batcher and the strong point of this sorting procedure is that it is very suitable for a hard-wired implementation using a sorting network. This paper presents a meta algorithm called Oyelami’s Sort that combines the technique of Bidirectional Bubble Sort with a modified diminishing increment sorting. The results from the implementation of the algorithm compared with Batcher’s Odd-Even Sort and Batcher’s Bitonic Sort showed that the algorithm performed better than the two in the worst case scenario. The implication is that the algorithm is faster.
    [Show full text]
  • Bubble Sort: an Archaeological Algorithmic Analysis
    Bubble Sort: An Archaeological Algorithmic Analysis Owen Astrachan 1 Computer Science Department Duke University [email protected] Abstract 1 Introduction Text books, including books for general audiences, in- What do students remember from their first program- variably mention bubble sort in discussions of elemen- ming courses after one, five, and ten years? Most stu- tary sorting algorithms. We trace the history of bub- dents will take only a few memories of what they have ble sort, its popularity, and its endurance in the face studied. As teachers of these students we should ensure of pedagogical assertions that code and algorithmic ex- that what they remember will serve them well. More amples used in early courses should be of high quality specifically, if students take only a few memories about and adhere to established best practices. This paper is sorting from a first course what do we want these mem- more an historical analysis than a philosophical trea- ories to be? Should the phrase Bubble Sort be the first tise for the exclusion of bubble sort from books and that springs to mind at the end of a course or several courses. However, sentiments for exclusion are sup- years later? There are compelling reasons for excluding 1 ported by Knuth [17], “In short, the bubble sort seems discussion of bubble sort , but many texts continue to to have nothing to recommend it, except a catchy name include discussion of the algorithm after years of warn- and the fact that it leads to some interesting theoreti- ings from scientists and educators.
    [Show full text]
  • Data Structures & Algorithms
    DATA STRUCTURES & ALGORITHMS Tutorial 6 Questions SORTING ALGORITHMS Required Questions Question 1. Many operations can be performed faster on sorted than on unsorted data. For which of the following operations is this the case? a. checking whether one word is an anagram of another word, e.g., plum and lump b. findin the minimum value. c. computing an average of values d. finding the middle value (the median) e. finding the value that appears most frequently in the data Question 2. In which case, the following sorting algorithm is fastest/slowest and what is the complexity in that case? Explain. a. insertion sort b. selection sort c. bubble sort d. quick sort Question 3. Consider the sequence of integers S = {5, 8, 2, 4, 3, 6, 1, 7} For each of the following sorting algorithms, indicate the sequence S after executing each step of the algorithm as it sorts this sequence: a. insertion sort b. selection sort c. heap sort d. bubble sort e. merge sort Question 4. Consider the sequence of integers 1 T = {1, 9, 2, 6, 4, 8, 0, 7} Indicate the sequence T after executing each step of the Cocktail sort algorithm (see Appendix) as it sorts this sequence. Advanced Questions Question 5. A variant of the bubble sorting algorithm is the so-called odd-even transposition sort . Like bubble sort, this algorithm a total of n-1 passes through the array. Each pass consists of two phases: The first phase compares array[i] with array[i+1] and swaps them if necessary for all the odd values of of i.
    [Show full text]
  • Parallel Sorting Algorithms + Topic Overview
    + Design of Parallel Algorithms Parallel Sorting Algorithms + Topic Overview n Issues in Sorting on Parallel Computers n Sorting Networks n Bubble Sort and its Variants n Quicksort n Bucket and Sample Sort n Other Sorting Algorithms + Sorting: Overview n One of the most commonly used and well-studied kernels. n Sorting can be comparison-based or noncomparison-based. n The fundamental operation of comparison-based sorting is compare-exchange. n The lower bound on any comparison-based sort of n numbers is Θ(nlog n) . n We focus here on comparison-based sorting algorithms. + Sorting: Basics What is a parallel sorted sequence? Where are the input and output lists stored? n We assume that the input and output lists are distributed. n The sorted list is partitioned with the property that each partitioned list is sorted and each element in processor Pi's list is less than that in Pj's list if i < j. + Sorting: Parallel Compare Exchange Operation A parallel compare-exchange operation. Processes Pi and Pj send their elements to each other. Process Pi keeps min{ai,aj}, and Pj keeps max{ai, aj}. + Sorting: Basics What is the parallel counterpart to a sequential comparator? n If each processor has one element, the compare exchange operation stores the smaller element at the processor with smaller id. This can be done in ts + tw time. n If we have more than one element per processor, we call this operation a compare split. Assume each of two processors have n/p elements. n After the compare-split operation, the smaller n/p elements are at processor Pi and the larger n/p elements at Pj, where i < j.
    [Show full text]
  • A Proposed Solution for Sorting Algorithms Problems by Comparison Network Model of Computation
    International Journal of Scientific & Engineering Research Volume 3, Issue 4, April-2012 1 ISSN 2229-5518 A Proposed Solution for Sorting Algorithms Problems by Comparison Network Model of Computation. Mr. Rajeev Singh, Mr. Ashish Kumar Tripathi, Mr. Saurabh Upadhyay, Mr.Sachin Kumar Dhar Dwivedi Abstract:-In this paper we have proposed a new solution for sorting algorithms. In the beginning of the sorting algorithm for serial computers (Random access machines, or RAM’S) that allow only one operation to be executed at a time. We have investigated sorting algorithm based on a comparison network model of computation, in which many comparison operation can be performed simultaneously. Index Terms Sorting algorithms, comparison network, sorting network, the zero one principle, bitonic sorting network 1 Introduction 1.2 The output is a permutation, or reordering, of the input. There are many algorithms for solving sorting algorithms For example of bubble sort 8, 25,9,3,6 (networks).A sorting network is an abstract mathematical model of a network of wires and comparator modules that is used to sort 8 8 8 3 3 a sequence of numbers. Each comparator connects two wires and sorts the values by outputting the smaller value to one wire and 25 25 9 9 3 8 6 6 the large to the other. A sorting network consists of two items comparators and wires .each wires carries with its values and each 9 25 3 9 6 8 comparator takes two wires as input and output. This independence of comparison sequences is useful for parallel 3 25 6 9 execution of the algorithms.
    [Show full text]
  • Sorting Networks
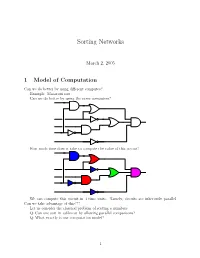
    Sorting Networks March 2, 2005 1 Model of Computation Can we do better by using different computes? Example: Macaroni sort. Can we do better by using the same computers? How much time does it take to compute the value of this circuit? We can compute this circuit in 4 time units. Namely, circuits are inherently parallel. Can we take advantage of this??? Let us consider the classical problem of sorting n numbers. Q: Can one sort in sublinear by allowing parallel comparisons? Q: What exactly is our computation model? 1 1.1 Computing with a circuit We are going to design a circuit, where the inputs are the numbers, and we compare two numbers using a comparator gate: ¢¤¦© ¡ ¡ Comparator ¡£¢¥¤§¦©¨ ¡ For our drawings, we will draw such a gate as follows: ¢¡¤£¦¥¨§ © ¡£¦ So, circuits would just be horizontal lines, with vertical segments (i.e., gates) between them. A complete sorting network, looks like: The inputs come on the wires on the left, and are output on the wires on the right. The largest number is output on the bottom line. The surprising thing, is that one can generate circuits from a sorting algorithm. In fact, consider the following circuit: Q: What does this circuit does? A: This is the inner loop of insertion sort. Repeating this inner loop, we get the following sorting network: 2 Alternative way of drawing it: Q: How much time does it take for this circuit to sort the n numbers? Running time = how many time clocks we have to wait till the result stabilizes. In this case: 5 1 2 3 4 6 7 8 9 In general, we get: Lemma 1.1 Insertion sort requires 2n − 1 time units to sort n numbers.
    [Show full text]
  • 13 Basic Sorting Algorithms
    Concise Notes on Data Structures and Algorithms Basic Sorting Algorithms 13 Basic Sorting Algorithms 13.1 Introduction Sorting is one of the most fundamental and important data processing tasks. Sorting algorithm: An algorithm that rearranges records in lists so that they follow some well-defined ordering relation on values of keys in each record. An internal sorting algorithm works on lists in main memory, while an external sorting algorithm works on lists stored in files. Some sorting algorithms work much better as internal sorts than external sorts, but some work well in both contexts. A sorting algorithm is stable if it preserves the original order of records with equal keys. Many sorting algorithms have been invented; in this chapter we will consider the simplest sorting algorithms. In our discussion in this chapter, all measures of input size are the length of the sorted lists (arrays in the sample code), and the basic operation counted is comparison of list elements (also called keys). 13.2 Bubble Sort One of the oldest sorting algorithms is bubble sort. The idea behind it is to make repeated passes through the list from beginning to end, comparing adjacent elements and swapping any that are out of order. After the first pass, the largest element will have been moved to the end of the list; after the second pass, the second largest will have been moved to the penultimate position; and so forth. The idea is that large values “bubble up” to the top of the list on each pass. A Ruby implementation of bubble sort appears in Figure 1.
    [Show full text]
  • Sorting Partnership Unless You Sign Up! Brian Curless • Homework #5 Will Be Ready After Class, Spring 2008 Due in a Week
    Announcements (5/9/08) • Project 3 is now assigned. CSE 326: Data Structures • Partnerships due by 3pm – We will not assume you are in a Sorting partnership unless you sign up! Brian Curless • Homework #5 will be ready after class, Spring 2008 due in a week. • Reading for this lecture: Chapter 7. 2 Sorting Consistent Ordering • Input – an array A of data records • The comparison function must provide a – a key value in each data record consistent ordering on the set of possible keys – You can compare any two keys and get back an – a comparison function which imposes a indication of a < b, a > b, or a = b (trichotomy) consistent ordering on the keys – The comparison functions must be consistent • Output • If compare(a,b) says a<b, then compare(b,a) must say b>a • If says a=b, then must say b=a – reorganize the elements of A such that compare(a,b) compare(b,a) • If compare(a,b) says a=b, then equals(a,b) and equals(b,a) • For any i and j, if i < j then A[i] ≤ A[j] must say a=b 3 4 Why Sort? Space • How much space does the sorting • Allows binary search of an N-element algorithm require in order to sort the array in O(log N) time collection of items? • Allows O(1) time access to kth largest – Is copying needed? element in the array for any k • In-place sorting algorithms: no copying or • Sorting algorithms are among the most at most O(1) additional temp space.
    [Show full text]
  • Foundations of Differentially Oblivious Algorithms
    Foundations of Differentially Oblivious Algorithms T-H. Hubert Chan Kai-Min Chung Bruce Maggs Elaine Shi August 5, 2020 Abstract It is well-known that a program's memory access pattern can leak information about its input. To thwart such leakage, most existing works adopt the technique of oblivious RAM (ORAM) simulation. Such an obliviousness notion has stimulated much debate. Although ORAM techniques have significantly improved over the past few years, the concrete overheads are arguably still undesirable for real-world systems | part of this overhead is in fact inherent due to a well-known logarithmic ORAM lower bound by Goldreich and Ostrovsky. To make matters worse, when the program's runtime or output length depend on secret inputs, it may be necessary to perform worst-case padding to achieve full obliviousness and thus incur possibly super-linear overheads. Inspired by the elegant notion of differential privacy, we initiate the study of a new notion of access pattern privacy, which we call \(, δ)-differential obliviousness". We separate the notion of (, δ)-differential obliviousness from classical obliviousness by considering several fundamental algorithmic abstractions including sorting small-length keys, merging two sorted lists, and range query data structures (akin to binary search trees). We show that by adopting differential obliv- iousness with reasonable choices of and δ, not only can one circumvent several impossibilities pertaining to full obliviousness, one can also, in several cases, obtain meaningful privacy with little overhead relative to the non-private baselines (i.e., having privacy \almost for free"). On the other hand, we show that for very demanding choices of and δ, the same lower bounds for oblivious algorithms would be preserved for (, δ)-differential obliviousness.
    [Show full text]
  • Selected Sorting Algorithms
    Selected Sorting Algorithms CS 165: Project in Algorithms and Data Structures Michael T. Goodrich Some slides are from J. Miller, CSE 373, U. Washington Why Sorting? • Practical application – People by last name – Countries by population – Search engine results by relevance • Fundamental to other algorithms • Different algorithms have different asymptotic and constant-factor trade-offs – No single ‘best’ sort for all scenarios – Knowing one way to sort just isn’t enough • Many to approaches to sorting which can be used for other problems 2 Problem statement There are n comparable elements in an array and we want to rearrange them to be in increasing order Pre: – An array A of data records – A value in each data record – A comparison function • <, =, >, compareTo Post: – For each distinct position i and j of A, if i < j then A[i] ≤ A[j] – A has all the same data it started with 3 Insertion sort • insertion sort: orders a list of values by repetitively inserting a particular value into a sorted subset of the list • more specifically: – consider the first item to be a sorted sublist of length 1 – insert the second item into the sorted sublist, shifting the first item if needed – insert the third item into the sorted sublist, shifting the other items as needed – repeat until all values have been inserted into their proper positions 4 Insertion sort • Simple sorting algorithm. – n-1 passes over the array – At the end of pass i, the elements that occupied A[0]…A[i] originally are still in those spots and in sorted order.
    [Show full text]