A Single Population Mean Using the Normal Distribution∗
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Good for Enterprise – Android V1.9.1 Release Notes (Service Release)
Good for Enterprise – Android v1.9.1 Release Notes (Service Release) Updated: April 27, 2012 Good for Enterprise – Android v1.9.1 (Service Release) .............................................................................................. 1 Issues Resolved ........................................................................................................................................................ 1 Good for Enterprise – Android v1.9.0 ........................................................................................................................... 1 New Features ............................................................................................................................................................ 1 Issues Resolved ........................................................................................................................................................ 2 Good for Enterprise – Android v1.8.1 (Service Release) .............................................................................................. 2 Good for Enterprise – Android v1.8.0 ........................................................................................................................... 3 New Features ............................................................................................................................................................ 3 Good for Enterprise – Android v1.7.5 Service Release ................................................................................................ 3 -

77017 20268 Comprehensive Telecommunications Services
Corning Tower, Empire State Plaza, Albany, NY 12242 | www.nyspro.ogs.ny.gov | [email protected] | 518-474-6717 Contract Award Notification Update Subject: Contact Information & Price List Update DATE: September 7, 2018 AWARD #: 20268 Group # 77017 AWARD DESCRIPTION: Comprehensive Telecommunications Services CONTRACT PERIOD: August 16, 2007 (various) – August 15, 2018 (or as Extended to May 19, 2019) CONTACT: Shannon Prica - Kast | 518-473-0482 | [email protected] CONTRACT NO: PS67518 CONTRACTOR: Crown Castle Fiber LLC PS63070 Paetec Communications LLC PS63853 Sprint Solutions Inc CONTACT INFORMATION: The above Contractors have updated their Contact Information as follows: CONTRACT #: CONTRACTOR: MODIFICATION: PS67518 Crown Castle Fiber LLC F/K/A The name of the company was changed Lightower Fiber Networks II LLC from Lightower Fiber Networks II LLC to Crown Castle Fiber LLC. PS63070 Paetec Communications LLC The company’s address was changed. Contract Services contacts, Account Development contacts and Sales contacts have been amended. PS63853 Sprint Solutions Inc Contact information for the Regional Manager has been added. One of the Public Sector Account Managers has been removed. PRICE LIST: The above Contractors have updated their Price List as follows: CONTRACT #: CONTRACTOR: MODIFICATION: PS67518 Crown Castle Fiber LLC F/K/A The name of the company was changed Lightower Fiber Networks II LLC from Lightower Fiber Networks II LLC to Crown Castle Fiber LLC. Please access the following link for purposes of viewing the CTS contracts referenced above http://www.ogs.ny.gov/purchase/snt/awardnotes/7701720268.pdf. All other terms and conditions of the original Contract Award Notification (CAN) remain the same. -

Contract # PS63853
Comprehensive Telecommunication Services Sprint 1 of 64 Group # 77017 Award # 20268 Contract # PS63853 Contract Comprehensive Telecommunications Services Group Number 77017 Award Number 20268 Contract Number PS63853 Contractor Sprint Service Long Distance Lot 1 Statewide or Regional Statewide 5/2/2017 One-Time Installation Monthly Service, Function or Device Increment Minutes Recurring Per 1st 18 Seconds Per Additional 6 Per 1st Minute Per Additional Increment Cost (4- Seconds Increment Cost (4- Minute decimal) Increment Cost (4- decimal) Increment Cost (4- decimal) decimal) Interstate: On-On $ 0.0048 $ 0.0016 $ 0.0160 $ 0.0160 On-Off $ 0.0054 $ 0.0018 $ 0.0180 $ 0.0180 Off-On $ 0.0054 $ 0.0018 $ 0.0180 $ 0.0180 Off-Off $ 0.0099 $ 0.0033 $ 0.0330 $ 0.0330 Intrastate New York: On-On $ 0.0075 $ 0.0025 $ 0.0250 $ 0.0250 On-Off $ 0.0122 $ 0.0041 $ 0.0406 $ 0.0406 Off-On $ 0.0122 $ 0.0041 $ 0.0406 $ 0.0406 Off-Off $ 0.0199 $ 0.0066 $ 0.0663 $ 0.0663 IntraLATA New York: On-On $ 0.0075 $ 0.0025 $ 0.0250 $ 0.0250 On-Off $ 0.0122 $ 0.0041 $ 0.0406 $ 0.0406 Off-On $ 0.0122 $ 0.0041 $ 0.0406 $ 0.0406 Off-Off $ 0.0199 $ 0.0066 $ 0.0663 $ 0.0663 International Service Dedicated Switched Destination Country Per 1st 30 Second Per Additional 6 Per 1st 30 Second Per Additional 6 Additional Mobile Increment Cost Second Increment Cost Second Termination Increment Cost Increment Cost Per Minute Increment Cost Argentina $ 0.0965 $ 0.0193 $ 0.1040 $ 0.0208 $ 0.1250 Australia $ 0.0205 $ 0.0041 $ 0.0280 $ 0.0056 $ 0.1510 Brazil $ 0.0415 $ 0.0083 $ 0.0490 $ 0.0098 -
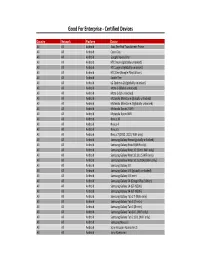
MMS Copy of Supported Devices
Good For Enterprise ‐ Certified Devices Country Network Platform Device All All Android Asus Eee Pad Transformer Prime All All Android Cisco Cius All All Android Google Nexus One All All Android HTC Desire (globally unlocked) All All Android HTC Legend (globally unlocked) All All Android HTC One (Google Play Edition) All All Android Kindle Fire All All Android LG Optimus 2X (globally unlocked) All All Android Moto G (Global unlocked) All All Android Moto G (US unlocked) All All Android Motorola Milestone (globally unlocked) All All Android Motorola Milestone 2 (globally unlocked) All All Android Motorola Xoom 2 WiFi All All Android Motorola Xoom WiFi All All Android Nexus 10 All All Android Nexus 4 All All Android Nexus 5 All All Android Nexus 7 (2012, 2013, WiFi only) All All Android Samsung Galaxy Nexus (globally unlocked) All All Android Samsung Galaxy Note 8 (WiFi only) All All Android Samsung Galaxy Note 10.1 (Intl. WiFi only) All All Android Samsung Galaxy Note 10.1 (U.S WiFi only) All All Android Samsung Galaxy Note 10.1 (2014) (WiFi only) All All Android Samsung Galaxy S II All All Android Samsung Galaxy S III (globally unlocked) All All Android Samsung Galaxy S III mini All All Android Samsung Galaxy S4 (Google Play Edition) All All Android Samsung Galaxy S4 (GT‐I9500) All All Android Samsung Galaxy S4 (GT‐I9505) All All Android Samsung Galaxy Tab 2 7 (WiFi only) All All Android Samsung Galaxy Tab 3 (7‐inch) All All Android Samsung Galaxy Tab 3 (8‐inch) All All Android Samsung Galaxy Tab 10.1 (WiFi only) All All Android Samsung -

Udynamo Compatibility List
uDynamo Compatibility List Reader Manuf. Device Name Alt. Model Info Model Info OS OS Version Carrier Date Added Date Tested Type iDynamo 5 Apple iPad Air 2 Lightning N/A iOS N/A N/A Tablet iDynamo 5 Apple iPad Air* Lightning N/A iOS N/A N/A Tablet iDynamo 5 Apple iPad with Retina Display* Lightning N/A iOS N/A N/A Tablet iDynamo 5 Apple iPad mini 3 Lightning N/A iOS N/A N/A Tablet iDynamo 5 Apple iPad mini 2 Lightning N/A iOS N/A N/A Tablet iDynamo 5 Apple iPad mini* Lightning N/A iOS N/A N/A Tablet iDynamo 5 Apple iPhone 5c* Lightning N/A iOS N/A N/A Phone iDynamo 5 Apple iPhone 5s* Lightning N/A iOS N/A N/A Phone iDynamo 5 Apple iPhone 5* Lightning N/A iOS N/A N/A Phone iDynamo 5 Apple iPod touch (5th* generation) Lightning N/A iOS N/A N/A iPod iDynamo 5 Apple iPhone 6* Lightning N/A iOS N/A N/A Phone iDynamo 5 Apple iPhone 6 Plus* Lightning N/A iOS N/A N/A Phone iDynamo Apple iPad (3rd generation) 30 PIN N/A iOS N/A N/A Tablet iDynamo Apple iPad 2 30 PIN N/A iOS N/A N/A Tablet iDynamo Apple iPad 30 PIN N/A iOS N/A N/A Tablet iDynamo Apple iPhone 4s 30 PIN N/A iOS N/A N/A Phone iDynamo Apple iPhone 4 30 PIN N/A iOS N/A N/A Phone iDynamo Apple iPhone 3GS 30 PIN N/A iOS N/A N/A Phone iDynamo Apple iPod touch (3rd and 4th generation) 30 PIN N/A iOS N/A N/A iPod uDynamo Acer liquid MT liquid MT Android 2.3.6 101.18 1/24/14 1/24/14 uDynamo Alcatel Alcatel OneTouch Fierce 7024W Android 4.2.2 101.18 3/6/14 3/6/14 uDynamo ALCATEL Megane ALCATEL ONE TOUCH 5020T Android 4.1.2 101.18 8/10/15 8/10/15 uDynamo ALCATEL ALCATEL ONE TOUCH IDOL X ALCATEL -

Purchasing Memorandum
New York State Office Of General Services Procurement Services Group Corning Tower Building Empire State Plaza Albany, New York 12242 http://www.ogs.ny.gov PURCHASING MEMORANDUM CONTRACT AWARD NOTIFICATION UPDATE AWARD NUMBER: 20268 DATE: October 28, 2011 PLEASE ADDRESS INQUIRIES TO: GROUP: 77017 STATE AGENCIES & CONTRACTORS Comprehensive Telecommunications Services Karen Rogers Purchasing Officer I (518) 486-9298 [email protected] CONTRACTORS: CONTRACT NOS: OTHER AUTHORIZED USERS CONTRACT PERIODS: Customer Services (518) 474-6717 [email protected] Sprint Solutions, Inc. – PS63853 – 05-09-2008 – 08-15-2017 Paetec Communications – PS63070 – 08-16-2007 – 08-15-2017 SUBJECT: Update Product/Service List (Sprint Solutions, Inc.) Update Product/Service List (Paetec Communications) ALL STATE AGENCIES AND OTHERS AUTHORIZED TO USE STATE CONTRACTS: SPRINT SOLUTIONS, INC. has requested and the State has approved the following updates to its NYS Product/Services Price List: 1. iDEN NDC on Nextel A. Motorola i1 Promotional Price $169.99 ends 11/12/11 B. New Motorola Titanium Promotional Price $169.99 ends 11/12/11 C. I365 Promotional Price $117.99 ends 11/12/11 D. I576 Promotional Price $89.99 ends 11/12/11 E. I686 Promotional Price $130.99 ends 11/12/11 F. I886 Promotional Price $99.99 ends 11/12/11 G. Blackberry 8350i Promotional Price ends 11/12/11 H. No Longer Available: i776, i465 Clutch, Motorola i890, Motorola Brute i680, I. Stature i9 2. CDMA Vision A. End of Life: Samsung Seek, LG Rumor, Samsung M240 B. New Kyocera Brio Promotional Price Free ends 11/12/11 C. -

Device Compaibility List
Device Compatibility G4X Mobile Card Reader Asus Eee Pad Transformer N/A LG Ally Verizon Motorola Photon Sprint HTC Aria AT&T LG Enlighten Verizon Motorola Xoom Wi-Fi HTC Droid Eris Verizon LG G-Slate T-Mobile Motorola Xoom 4G Verizon HTC Droid Incredible Verizon LG G2X T-Mobile Pantech Breakout Verizon (AMOLED) HTC Droid Incredible (SLCD) Verizon LG Lucid Verizon Pantech Burst AT&T HTC Droid Incredible 2 Verizon LG Marquee Sprint Samsung Captivate AT&T HTC EVO 3D Sprint LG Mytouch Q T-Mobile Samsung Conquer 4G Sprint HTC EVO 4G (h/w ver. 0003) Sprint LG Nexus T-Mobile Samsung Continuum Verizon HTC EVO 4G LTE Sprint LG Nexus 4 T-Mobile Samsung Droid Charge Verizon HTC EVO Shift 4G Sprint LG Optimus Elite Sprint Samsung Epic 4G Sprint HTC EVO View 4G Sprint LG Optimus G AT&T Samsung Exhilarate AT&T HTC G2 T-Mobile LG Optimus S Sprint Samsung Fascinate Verizon HTC Inspire 4G AT&T LG Optimus T T-Mobile Samsung Galaxy Nexus Verizon HTC Jetstream AT&T LG Phoenix AT&T Samsung Galaxy Note AT&T HTC myTouch 4G T-Mobile LG Revolution Verizon Samsung Galaxy Note 10.1 Wi-Fi HTC myTouch 4G Slide T-Mobile LG Spectrum Verizon Samsung Galaxy S 4G T-Mobile HTC Nexus One AT&T LG Thrill 4G AT&T Samsung Galaxy S II T-Mobile Samsung Galaxy S II Epic 4G HTC Nexus One T-Mobile LG Viper 4G LTE Sprint Sprint Touch Samsung Galaxy S II HTC One S AT&T LG Vortex Verizon AT&T Skyrocket HTC One X AT&T Motorola Admiral Sprint Samsung Galaxy S III Verizon HTC Rezound Verizon Motorola Atrix 4G AT&T Samsung Galaxy S III AT&T HTC Rhyme Verizon Motorola Citrus Verizon Samsung Galaxy S III Sprint HTC Sensation 4G T-Mobile Motorola Droid 2 Verizon Samsung Galaxy Tab 3G Sprint HTC Status AT&T Motorola Droid 2 Global Verizon Samsung Galaxy Tab 10.1 Wi-Fi HTC Thunderbolt Verizon Motorola Droid 3 Verizon Samsung Galaxy Tab 10.1 4G Verizon HTC Wildfire S T-Mobile Motorola Droid 4 Verizon Samsung Galaxy Tab 10.1 Verizon Huawei Ascend II (M865) U.S. -

Supported Android Devices AT&T KDDI Minor Carriers / Other
AT&T Appendix Acer Iconia Tab A501 (A501) A – HTC Aria (LIBERTY) Supported HTC Lele (HTCPH06130) Android HTC Nexus One (NEXUSONE) HTC One VX (HTCPM36100) Devices HTC One X (HTCONEX) HTC Status (HTCSTATUS) HTC Vivid (HTCPH39100) Huawei Impulse 4G (HUAWEIU8800-51) LG Eclipse (LG-E970) LG Escape 4G (LG-P870) LG Nitro HD (LG-P930) LG Phoenix (LG-P505) LG Thrill 3D (LG-P925) LG Thrive (LG-P506) Motorola Atrix 2 (MB865) Motorola Atrix 3 (MB886) Motorola Bravo MB520 (MB520) Motorola FlipSide (MB508) Pantech Crossover (PANTECHP8000) Samsung Captivate (SAMSUNG-SGH-I897) Samsung Captivate Glide (SAMSUNG-SGH-I927) Samsung Galaxy Express (SAMSUNG-SGH-I437) Samsung Galaxy Note (SAMSUNG-SGH-I717) Samsung Galaxy Note II (SGH-I317) Samsung Galaxy Rugby Pro (SAMSUNG-SGH-I547) Samsung Galaxy S II (SAMSUNG-SGH-I777) Samsung Galaxy S III (SAMSUNG-SGH-I747) Samsung Galaxy S4 (SAMSUNG-SGH-I337) Samsung Galaxy Tab 8.9 (SGH-I957) Samsung Galaxy Tab 8.9 (SAMSUNG-SGH-I957) Samsung Rugby (SAMSUNG-SGH-I847) Samsung SkyRocket (SAMSUNG-SGH-I727) Sony Xperia T (LT30AT) KDDI HTC EVO 3D (ISW12HT) Minor Carriers / Other* LG Nexus 4 (NEXUS4) LG Optimus One (LG-P500) Motorola RAZR i (XT890) Samsung Galaxy Ace (GT-S5830) Samsung Galaxy SII LTE (SGH-I727R) Samsung Galaxy S III (GT-I9300) * Other denotes a device that is not officially carried by a network and is usually purchased unlocked. 1 Version 15 Sprint HTC EVO 3D (PG86100) HTC EVO 4G (PC36100) HTC EVO 4G LTE (EVO) HTC EVO Shift 4G (PG06100) HTC EVO View 4G (PG41200) HTC Hero (HERO200) HTC One (HTCONE) Kyocera ECHO -

Row Labels Sum of Units Sum of Wholesale AZPAL0752 1325 13759.63344
Row Labels Sum of Units Sum of Wholesale AZPAL0752 1325 13759.63344 Category GL PalletId ItemId IDType Description Wholesale Units Electronics 328 AZPAL0752 Asin B0090SGE4O BD 354015 Falcon Polypropylene Sterile Disposable Sample Container with Lid, 8 oz Capacity (Case of 100) 108.86 1 Electronics 107 AZPAL0752 UPC 848227006067 Zing Revolution MS-TRUB60274 True Blood - Eric Northman Cell Phone Cover Skin for Samsung Fascinate Galaxy S (SCH-I500) 6.59 1 Electronics 107 AZPAL0752 UPC 848227006067 Zing Revolution MS-TRUB60274 True Blood - Eric Northman Cell Phone Cover Skin for Samsung Fascinate Galaxy S (SCH-I500) 6.59 1 Electronics 107 AZPAL0752 UPC 848227002984 Zing Revolution MS-TRUB50215 True Blood - Cast Cell Phone Cover Skin for Samsung Epic 4G Galaxy S (SPH-D700) 6.59 1 Electronics 107 AZPAL0752 UPC 848227002984 Zing Revolution MS-TRUB50215 True Blood - Cast Cell Phone Cover Skin for Samsung Epic 4G Galaxy S (SPH-D700) 6.59 1 Electronics 107 AZPAL0752 UPC 848227002984 Zing Revolution MS-TRUB50215 True Blood - Cast Cell Phone Cover Skin for Samsung Epic 4G Galaxy S (SPH-D700) 6.59 1 Electronics 107 AZPAL0752 UPC 848227002984 Zing Revolution MS-TRUB50215 True Blood - Cast Cell Phone Cover Skin for Samsung Epic 4G Galaxy S (SPH-D700) 6.59 1 Electronics 107 AZPAL0752 UPC 848227002984 Zing Revolution MS-TRUB50215 True Blood - Cast Cell Phone Cover Skin for Samsung Epic 4G Galaxy S (SPH-D700) 6.59 1 Electronics 107 AZPAL0752 UPC 847786076719 Zing Revolution MS-SPRK20133 South Park - Cartman Badass Cell Phone Cover Skin for iPhone 4/4S 6.59 -
REBATES Offers End 1/10/13
REBATES Offers end 1/10/13 $50 MAIL-IN REBATE INSTANT AND MAIL-IN SAVINGS VIA PREPAID REWARD CARD Smartphones with in-store activation, mail-in rebate via ® Prepaid Reward Card on select listed devices. BlackBerry Curve™ 8350i smartphone BlackBerry® Curve™ 3G smartphone BlackBerry® Curve™ 9350 smartphone BlackBerry® Torch™ 9850 smartphone Express from Sprint™ INSTANT SAVINGS AND REBATE Galaxy Nexus REQUIREMENTS: HTC Arrive™ HTC EVO™ 3D For new customers: HTC EVO Design 4G™ HTC EVO Shift™ 4G • Activation of a new line of service Kyocera Milano • A two-year Agreement KYOCERA Rise An activation fee of $36 per line will apply. LG Mach™ LG Marquee™ For existing qualified customers: LG Optimus Elite™ LG Optimus S™ • More than 22 consecutive months since LG Viper™ the subscriber’s last device discount MOTOROLA ADMIRAL™ • A new two-year Agreement MOTOROLA PHOTON™ 4G An upgrade fee of up to $36 per upgrade MOTOROLA TITANIUM™ may apply. Samsung Conquer™ 4G Samsung Epic™ 4G For more information on upgrade program offers, Samsung Galaxy S® II visit sprint.com/upgrades. Samsung Galaxy Victory™ Samsung Replenish™ Samsung Transform™ Samsung Transform™ Ultra ENJOY YOUR AMERICAN EXPRESS Sprint Flash™ ZTE Fury™ PREPAID REWARD CARD. Feature Phones You’ll receive your mail-in LG Rumor Reflex™ rebate via an American Express i335 by Motorola i576 by Motorola Prepaid Reward Card. The card i886 by Motorola can be used virtually anywhere Kyocera Brio Kyocera DuraCore American Express Cards are Kyocera DuraMax accepted in the U.S. Limitations Kyocera DuraPlus -
77017 20268 Comprehensive Telecommunications Services, Contract Updates
Corning Tower, Empire State Plaza, Albany, NY 12242 | https://ogs.ny.gov/procurement | [email protected] | 518-474-6717 Contract Award Notification Update Subject: Contract Expiration/Purchase Orders DATE: August 30, 2019 AWARD #: 20268 GROUP #: 77017 AWARD DESCRIPTION: Comprehensive Telecommunications Services August 16, 2007 (various) – August 15, 2018 (or as Extended to September 15, CONTRACT PERIOD: 2019) CONTACT: Steven Charles | 518-486-5354 | [email protected] CONTRACT NO.: Various CONTRACTOR: All present CTS Contractors CONTRACT EXTENSIONS END NOTICE: OGS is issuing this final notice that the Comprehensive Telecommunications Services contracts are due to expire on September 15, 2019. OGS has published Solicitation #23100 to establish a new award for Telecommunications Connectivity Services to replace the expiring contract. Authorized Users should plan accordingly and ensure they have issued any necessary Purchase Orders prior to the expiration of these contracts. Purchase Orders issued prior to the contract expiration date of September 15, 2019, may remain in effect through September 14, 2020. Please access the following link for purposes of viewing the Comprehensive Telecommunications Services contracts (award 20268) referenced above https://online.ogs.ny.gov/purchase/snt/awardnotes/7701720268can.htm All other terms and conditions remain the same. 20268p216 Corning Tower, Empire State Plaza, Albany, NY 12242 | https://ogs.ny.gov/procurement | [email protected] | 518-474-6717 Contract Award Notification -
Long Distance
Long Distance Contract Comprehensive Telecommunications Services Group Number 77017 Award Number 20268 Contract Number PS63853 Contractor Sprint Service Long Distance Lot 1 Statewide or Regional Statewide One-Time Installation Monthly Service, Function or Device Increment Minutes Recurring Per 1st 18 Seconds Per Additional 6 Per 1st Minute Per Additional Increment Cost (4- Seconds Increment Cost (4- Minute decimal) Increment Cost (4- decimal) Increment Cost (4- decimal) decimal) Interstate: On-On $ 0.0048 $ 0.0016 $ 0.0160 $ 0.0160 On-Off $ 0.0054 $ 0.0018 $ 0.0180 $ 0.0180 Off-On $ 0.0054 $ 0.0018 $ 0.0180 $ 0.0180 Off-Off $ 0.0099 $ 0.0033 $ 0.0330 $ 0.0330 Intrastate New York: On-On $ 0.0075 $ 0.0025 $ 0.0250 $ 0.0250 On-Off $ 0.0122 $ 0.0041 $ 0.0406 $ 0.0406 Off-On $ 0.0122 $ 0.0041 $ 0.0406 $ 0.0406 Off-Off $ 0.0199 $ 0.0066 $ 0.0663 $ 0.0663 IntraLATA New York: On-On $ 0.0075 $ 0.0025 $ 0.0250 $ 0.0250 On-Off $ 0.0122 $ 0.0041 $ 0.0406 $ 0.0406 Off-On $ 0.0122 $ 0.0041 $ 0.0406 $ 0.0406 Off-Off $ 0.0199 $ 0.0066 $ 0.0663 $ 0.0663 International Service Dedicated Switched Destination Country Per 1st 30 Second Per Additional 6 Per 1st 30 Second Per Additional 6 Additional Mobile Increment Cost Second Increment Cost Second Termination Increment Cost Increment Cost Per Minute Increment Cost Argentina $ 0.0965 $ 0.0193 $ 0.1040 $ 0.0208 $ 0.1250 Australia $ 0.0205 $ 0.0041 $ 0.0280 $ 0.0056 $ 0.1510 Brazil $ 0.0415 $ 0.0083 $ 0.0490 $ 0.0098 $ 0.1580 Canada $ 0.0200 $ 0.0040 $ 0.0275 $ 0.0055 $ - France $ 0.0220 $ 0.0044 $ 0.0295 $ 0.0059