DOCSLIB.ORG

Sample Written Theory Transfer Exam

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Sample Written Theory Transfer Exam Eastern Illinois University Page 1 of 4 Music Theory Transfer Examination Name: __________________________ e-mail: ________________________ SECTION I SAMPLE EXAM A. Identify the the key, the chords using Roman numerals, and the final cadence of the following chord progression. U bb c œ œ œ œ n˙ œ & b œ œ œ œ œ œ œ œ œ œ œ œ œ ? b nœ œ œ œ œ œ œ b b c œ œ œ u B. Continuing with the given voicing, realize the following figured bass progressions adding SAT. Please do not forget to identify the harmonic progression using Roman numerals and inversion numbers underneath the staves and identify the final cadence. bb œ & œ ? b œ ˙ b œ #œ ˙ ˙ ˙ ˙ ˙ ˙ w 6 #6 6 7 6 # 4 4 # 5 2 3 C. Find and mark the following errors in the four-part passage below: 1. Direct 8ve 2. Chord with no third 3. Spacing error 4. Parallel 8ves 5. Unresolved Leading Tone œ U & b œ œ œ œ œ œ œ #œ œ œ œ œ œ œ ? œ œ œ œ œ #œ œ b œ œ œ œ œ œ u SAMPLE-01-MusicTheory-TransferExam.musx Eastern Illinois University Page 2 of 4 Music Theory Transfer Examination SECTION II SAMPLE EXAM A. Identify the key, the chords using Roman numeral analysis, the non-chord tones (circle and identify by kind) and the final cadence of the following chorale phrase. ## œ œ œ œ œ & c œ œ #œ œ œ #œ #œ ˙. œ œ œ œ œ #˙. ? ## c œ œ œ œ œ œ ˙. B. Prepare and resolve each of the following seventh chords and identify the chords using Roman numerals within the given keys. # bb œ ## œ # & b œ œ #œ ? œ # # œ # œœ bbb œ # œ Eb: –––– –––– –––– f#: –––– –––– –––– e: –––– –––– –––– C. Continue with the given voicing, realize the following figured bass adding SAT. Please identify the key, the chords using Roman numerals, and the final cadence. b œ & b c œ œ ? b c b œ nœ œ bœ œ bœ œ œ w 6 4 6 4 6 7 5 n2 2 SAMPLE-02-MusicTheory-TransferExam.musx n Eastern Illinois University Page 3 of 4 Music Theory Transfer Examination SAMPLE EXAM SECTION III A. Analyze the following phrase, identifying the key, the harmonic progression using Roman numerals, and the cadence. œ œ bœ œ œ & C œ œ œ #œ œ œ œ œ bœ œ œ œ bœ #nœ ˙ œ œ œ œ œ œ œ bœ œ bœ œ œ œ œ ˙ ? œ bœ œ œ nœ C œ #œ œ œ œ bœ œ œ œ ˙ B. Continue from the given chord, write a four-measure modulating progression from B-flat minor to B in SATB texture, using an enharmonic interpretation of the German Augmented Sixth Chord as V7 or vice versa. Do not forget to identify the chords using Roman numerals and the final cadence. Also, please do not change the key signature but, use accidentals for the new key. b b œ & b b b c œ ? b œ b bbb c œ C. Continue with the given voicing, realize the following figured bass adding SAT. Please identify the key(s), the chords using Roman numerals, and the final cadence. ## œ & œ ? # œœ œ œ œ ˙ # œ œ œ œ œ œ #œ œ ˙ 4 6 6 #6 6 7 # 5 2 6 #4 # 2 SAMPLE-03-MusicTheory-TransferExam.musx Eastern Illinois University Page 4 of 4 Music Theory Transfer Examination SECTION IV SAMPLE EXAM A. Continuing from the given chord, write an enharmonic modulation from D Major to E-flat minor using a diminished seventh chord (in SATB texture, 4/4 time, 4 measures in length, using at least 12 chords). Do not forget to identify the chords using Roman numerals and the final cadence. Also, please do not change the key signature but, use accidentals for the new key. # œ & # c œ œ ? ## c œ B. Analyze the following chromatic chord progression using Roman numerals. Make sure that you can account for every sonority appropriately. # œ œ nœ œ bœ nœ w & # œ œ œ œ#œ œ œ nœ nœ œ œ nœ œ # œœ #œ bœ œ nœ #œ bw œ bœ œ œ œ #œ œ œ œ nœ œ nœ nœ #œ œ nœ œ nw ? # œ œ œ œ nœ œ œ bœ œ œ œ œ œ nœ # nœ nœ bw C. Answer the following questions: a.) True or false: The term “rounded” in the context of binary form refers the fact that the first section cadences in the tonic key. b.) True or false: The term “simple” in the context of binary form refers to the fact that the melodic or motivic material from the opening section does return at the end of the piece. c.) A movement consisting of a minuet, trio, and repetition of the minuet is considered a: _______________________________ d.) Circle the letter combination that illustrates five-part rondo form: 1.) AABBC, 2.) ABBBA, 3.) AABCA, or 4.) ABACA e.) True or false: In a rondo, an episode must always remain in the same key. f.) Which is not a part of an exposition? 1.) development, 2.) first theme group, 3.) transition, or 4.) second theme group g.) Circle he typical tonal organization of the exposition of a major-key sonata: 1.) I – iii – V, 2.) I – IV – V, 3.) I – V, or 4.) I – IV h.) Circle the typical tonal organization of the exposition of a minor-key sonata: 1.) i – V, 2.) i – iv, 3.) i – III, or 4.) i – VI i.) True or false: The primary function of the retransition is to modulate to the second tonal area? j.) Briefly describe the primary function of a Classical period development section: SAMPLE-04-MusicTheory-TransferExam.musx.
Load more

Recommended publications
  • The Care and Feeding of the WHOLE MUSICAL YOU! Created by the Students and Instructors of the New Trier Jazz Ensembles Program
    The Care and Feeding of the WHOLE MUSICAL YOU! Created by the students and instructors of the New Trier Jazz Ensembles Program The many domains of the whole musical you… TECHNICIAN LITERATE JAZZ MUSICIAN COMPOSER/ARRANGER IMPROVISER LISTENER CRITIC HISTORIAN PERFORMER Tools/resources needed to develop the whole musical you… desire goals time space guidance enjoyment DEVELOPING AS A TECHNICIAN Practice with a metronome Track your progress – make your assessment quantitative (numbers) Take small, measured steps Record yourself, and be critical (also be positive) Use SmartMusic as a scale-practicing companion Go bonkers with scales Be creative with scales (play scales in intervals, play scales through the entire range of your instrument, play scales starting on notes other than the tonic, remember that every scale also represents a chord for each note in that scale, find new patterns in your scales Challenge yourself – push your boundaries Use etudes and solo transcriptions to push yourself Use a metronome!!! DEVELOPING AS A LITERATE JAZZ MUSICIAN Practice sight-reading during every session Learn tunes (from the definitive recorded version when possible) Learn vocabulary Learn chords on the piano DEVELOPING AS A COMPOSER/ARRANGER Compose a melody Compose a chord progression Compose a melody on an established chord progression (called a contrafact) Re-harmonize an established melody Write an arrangement of an established melody DEVELOPING AS AN IMPROVISER Transcribe a solo Compose a solo for a tune you’re
    [Show full text]
  • Harmony Crib Sheets
    Jazz Harmony Primer General stuff There are two main types of harmony found in modern Western music: 1) Modal 2) Functional Modal harmony generally involves a static drone, riff or chord over which you have melodies with notes chosen from various scales. It’s common in rock, modern jazz and electronic dance music. It predates functional harmony, too. In some types of modal music – for example in jazz - you get different modes/chord scale sounds over the course of a piece. Chords and melodies can be drawn from these scales. This kind of harmony is suited to the guitar due to its open strings and retuning possibilities. We see the guitar take over as a songwriting instrument at about the same time as the modes become popular in pop music. Loop based music also encourages this kind of harmony. It has become very common in all areas of music since the late 20th century under the influence of rock and folk music, composers like Steve Reich, modal jazz pioneered by Miles Davis and John Coltrane, and influences from India, the Middle East and pre-classical Western music. Functional harmony is a development of the kind of harmony used by Bach and Mozart. Jazz up to around 1960 was primarily based on this kind of harmony, and jazz improvisation was concerned with the improvising over songs written by the classically trained songwriters and film composers of the era. These composers all played the piano, so in a sense functional harmony is piano harmony. It’s not really guitar shaped. When I talk about functional harmony I’ll mostly be talking about ways we can improvise and compose on pre-existing jazz standards rather than making up new progressions.
    [Show full text]
  • Chapter 12 Answer Key.Indd
    Chapter 12 Answer Key Applications Exercises 1. Spell and resolve dominant seventh chords in root position. Chord voic- ings should be either complete (C) or incomplete (IN), as indicated below the Roman numerals. © 2019 Taylor & Francis 2 Chapter 12 Answer Key 2. Spell and resolve inverted dominant seventh chords. All chords should be complete. Add any necessary inversion symbol to the tonic chord. 3. Spell and resolve leading-tone seventh chords in root position and inversion. Add any necessary inversion symbol to the tonic chord. © 2019 Taylor & Francis Chapter 12 Answer Key 3 4. Complete the following chord progression in four voices. Provide a syntactic analysis below the Roman numerals. The syntactic analysis is shown below the Roman numerals. The voicing of chords and voice leading between chords is variable. Brain Teaser What triad is shared by V7 and viiØ7? How do these two seventh chords differ in terms of their scale-degree contents? Answer: V7 and viiØ7 share the leading-tone triad (viiO). The two chords differ by 5ˆ (the root of V7) and 6ˆ (the seventh of viiØ7). 5ˆ and 6ˆ are a whole step apart (a half step in minor, where 6ˆ is the seventh of viiO7). Thinking Critically An incomplete triad or seventh chord is missing its fifth. Compared with other chord members (root, third, and seventh), why is it possible to omit the fifth (i.e., why is this particular chord member nonessential)? Discussion The root of a chord is necessary to identify the chord and its function, the third determines the quality of the chord (major or minor), and the seventh must be present for a chord to be an actual seventh chord (rather than a triad).
    [Show full text]
  • F(P,Q) = Ffeic(R+TQ)
    674 MATHEMA TICS: N. H. McCOY PR.OC. N. A. S. ON THE FUNCTION IN QUANTUM MECHANICS WHICH CORRESPONDS TO A GIVEN FUNCTION IN CLASSICAL MECHANICS By NEAL H. MCCoy DEPARTMENT OF MATHEMATICS, SMrTH COLLEGE Communicated October 11, 1932 Let f(p,q) denote a function of the canonical variables p,q of classical mechanics. In making the transition to quantum mechanics, the variables p,q are represented by Hermitian operators P,Q which, satisfy the com- mutation rule PQ- Qp = 'y1 (1) where Y = h/2ri and 1 indicates the unit operator. From group theoretic considerations, Weyll has obtained the following general rule for carrying a function over from classical to quantum mechanics. Express f(p,q) as a Fourier integral, f(p,q) = f feiC(r+TQ) r(,r)d(rdT (2) (or in any other way as a linear combination of the functions eW(ffP+T)). Then the function F(P,Q) in quantum mechanics which corresponds to f(p,q) is given by F(P,Q)- ff ei(0P+7Q) t(cr,r)dodr. (3) It is the purpose of this note to obtain an explicit expression for F(P,Q), and although we confine our statements to the case in which f(p,q) is a polynomial, the results remain formally correct for infinite series. Any polynomial G(P,Q) may, by means of relation (1), be written in a form in which all of the Q-factors occur on the left in each term. This form of the function G(P,Q) will be denoted by GQ(P,Q).
    [Show full text]
  • Theory Placement Examination (D
    SAMPLE Placement Exam for Incoming Grads Name: _______________________ (Compiled by David Bashwiner, University of New Mexico, June 2013) WRITTEN EXAM I. Scales Notate the following scales using accidentals but no key signatures. Write the scale in both ascending and descending forms only if they differ. B major F melodic minor C-sharp harmonic minor II. Key Signatures Notate the following key signatures on both staves. E-flat minor F-sharp major Sample Graduate Theory Placement Examination (D. Bashwiner, UNM, 2013) III. Intervals Identify the specific interval between the given pitches (e.g., m2, M2, d5, P5, A5). Interval: ________ ________ ________ ________ ________ Note: the sharp is on the A, not the G. Interval: ________ ________ ________ ________ ________ IV. Rhythm and Meter Write the following rhythmic series first in 3/4 and then in 6/8. You may have to break larger durations into smaller ones connected by ties. Make sure to use beams and ties to clarify the meter (i.e. divide six-eight bars into two, and divide three-four bars into three). 2 Sample Graduate Theory Placement Examination (D. Bashwiner, UNM, 2013) V. Triads and Seventh Chords A. For each of the following sonorities, indicate the root of the chord, its quality, and its figured bass (being sure to include any necessary accidentals in the figures). For quality of chord use the following abbreviations: M=major, m=minor, d=diminished, A=augmented, MM=major-major (major triad with a major seventh), Mm=major-minor, mm=minor-minor, dm=diminished-minor (half-diminished), dd=fully diminished. Root: Quality: Figured Bass: B.
    [Show full text]
  • Many of Us Are Familiar with Popular Major Chord Progressions Like I–IV–V–I
    Many of us are familiar with popular major chord progressions like I–IV–V–I. Now it’s time to delve into the exciting world of minor chords. Minor scales give flavor and emotion to a song, adding a level of musical depth that can make a mediocre song moving and distinct from others. Because so many of our favorite songs are in major keys, those that are in minor keys1 can stand out, and some musical styles like rock or ​ ​ jazz thrive on complex minor scales and harmonic wizardry. Minor chord progressions generally contain richer harmonic possibilities than the typical major progressions. Minor key songs frequently modulate to major and back to minor. Sometimes the same chord can appear as major and minor in the very same song! But this heady harmonic mix is nothing to be afraid of. By the end of this article, you’ll not only understand how minor chords are made, but you’ll know some common minor chord progressions, how to write them, and how to use them in your own music. With enough listening practice, you’ll be able to recognize minor chord progressions in songs almost instantly! Table of Contents: 1. A Tale of Two Tonalities 2. Major or Minor? 3. Chords in Minor Scales 4. The Top 3 Chords in Minor Progressions 5. Exercises in Minor 6. Writing Your Own Minor Chord Progressions 7. Your Minor Journey 1 https://www.musical-u.com/learn/the-ultimate-guide-to-minor-keys A Tale of Two Tonalities Western music is dominated by two tonalities: major and minor.
    [Show full text]
  • Cadence in Music Version 1.9: Oct 4, 2007 12:24 Pm GMT-5
    Connexions module: m12402 1 Cadence in Music Version 1.9: Oct 4, 2007 12:24 pm GMT-5 Catherine Schmidt-Jones This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License ∗ Abstract A cadence is a place in a piece of music that feels like a stopping or resting point. In tonal music, cadences are classied by their chord progressions. Cadence in Music A cadence is any place in a piece of music that has the feel of an ending point. This can be either a strong, denite stopping point - the end of the piece, for example, or the end of a movement or a verse - but it also refers to the "temporary-resting-place" pauses that round o the ends of musical ideas within each larger section. A musical phrase1, like a sentence, usually contains an understandable idea, and then pauses before the next idea starts. Some of these musical pauses are simply take-a-breath- type pauses, and don't really give an "ending" feeling. In fact, like questions that need answers, many phrases leave the listener with a strong expectation of hearing the next, "answering", phrase. Other phrases, though, end with a more denite "we've arrived where we were going" feeling. The composer's expert control over such feelings of expectation and arrival are one of the main sources of the listener's enjoyment of the music. Like a story, a piece of music can come to an end by simply stopping, but most listeners will react to such abruptness with dissatisfaction: the story or music simply "stopped" instead of "ending" properly.
    [Show full text]
  • Day 17 AP Music Handout, Scale Degress.Mus
    Scale Degrees, Chord Quality, & Roman Numeral Analysis There are a total of seven scale degrees in both major and minor scales. Each of these degrees has a name which you are required to memorize tonight. 1 2 3 4 5 6 7 1 & w w w w w 1. tonicw 2.w supertonic 3.w mediant 4. subdominant 5. dominant 6. submediant 7. leading tone 1. tonic A triad can be built upon each scale degree. w w w w & w w w w w w w w 1. tonicw 2.w supertonic 3.w mediant 4. subdominant 5. dominant 6. submediant 7. leading tone 1. tonic The quality and scale degree of the triads is shown by Roman numerals. Captial numerals are used to indicate major triads with lowercase numerals used to show minor triads. Diminished triads are lowercase with a "degree" ( °) symbol following and augmented triads are capital followed by a "plus" ( +) symbol. Roman numerals written for a major key look as follows: w w w w & w w w w w w w w CM: wI (M) iiw (m) wiii (m) IV (M) V (M) vi (m) vii° (dim) I (M) EVERY MAJOR KEY FOLLOWS THE PATTERN ABOVE FOR ITS ROMAN NUMERALS! Because the seventh scale degree in a natural minor scale is a whole step below tonic instead of a half step, the name is changed to subtonic, rather than leading tone. Leading tone ALWAYS indicates a half step below tonic. Notice the change in the qualities and therefore Roman numerals when in the natural minor scale.
    [Show full text]
  • THE ZEROS of QUASI-ANALYTIC FUNCTIONS1 (3) H(V) = — F U-2 Log
    THE ZEROS OF QUASI-ANALYTICFUNCTIONS1 ARTHUR O. GARDER, JR. 1. Statement of the theorem. Definition 1. C(Mn, k) is the class of functions f(x) ior which there exist positive constants A and k and a sequence (Af„)"_0 such that (1) |/(n)(x)| ^AknM„, - oo < x< oo,» = 0,l,2, • • • . Definition 2. C(Mn, k) is a quasi-analytic class if 0 is the only element / of C(Mn, k) ior which there exists a point x0 at which /<">(*„)=0 for « = 0, 1, 2, ••• . We introduce the functions (2) T(u) = max u"(M„)_l, 0 ^ m < oo, and (3) H(v) = — f u-2 log T(u)du. T J l The following property of H(v) characterizes quasi-analytic classes. Theorem 3 [5, 78 ].2 Let lim,,.,*, M„/n= °o.A necessary and sufficient condition that C(Mn, k) be a quasi-analytic class is that (4) lim H(v) = oo, where H(v) is defined by (2) and (3). Definition 4. Let v(x) be a function satisfying (i) v(x) is continuously differentiable for 0^x< oo, (ii) v(0) = l, v'(x)^0, 0^x<oo, (iii) xv'(x)/v(x)=0 (log x)-1, x—>oo. We shall say that/(x)GC* if and only if f(x)EC(Ml, k), where M* = n\[v(n)]n and v(n) satisfies the above conditions. Definition 5. Let Z(u) be a real-valued function which is less Received by the editors November 29, 1954 and, in revised form, February 24, 1955. 1 Presented to the Graduate School of Washington University in partial fulfill- ment of the requirements for the degree of Doctor of Philosophy.
    [Show full text]
  • Music in Theory and Practice
    CHAPTER 4 Chords Harmony Primary Triads Roman Numerals TOPICS Chord Triad Position Simple Position Triad Root Position Third Inversion Tertian First Inversion Realization Root Second Inversion Macro Analysis Major Triad Seventh Chords Circle Progression Minor Triad Organum Leading-Tone Progression Diminished Triad Figured Bass Lead Sheet or Fake Sheet Augmented Triad IMPORTANT In the previous chapter, pairs of pitches were assigned specifi c names for identifi cation CONCEPTS purposes. The phenomenon of tones sounding simultaneously frequently includes group- ings of three, four, or more pitches. As with intervals, identifi cation names are assigned to larger tone groupings with specifi c symbols. Harmony is the musical result of tones sounding together. Whereas melody implies the Harmony linear or horizontal aspect of music, harmony refers to the vertical dimension of music. A chord is a harmonic unit with at least three different tones sounding simultaneously. Chord The term includes all possible such sonorities. Figure 4.1 #w w w w w bw & w w w bww w ww w w w w w w w‹ Strictly speaking, a triad is any three-tone chord. However, since western European music Triad of the seventeenth through the nineteenth centuries is tertian (chords containing a super- position of harmonic thirds), the term has come to be limited to a three-note chord built in superposed thirds. The term root refers to the note on which a triad is built. “C major triad” refers to a major Triad Root triad whose root is C. The root is the pitch from which a triad is generated. 73 3711_ben01877_Ch04pp73-94.indd 73 4/10/08 3:58:19 PM Four types of triads are in common use.
    [Show full text]
  • Consonance and Dissonance in Visual Music Bill Alves Harvey Mudd College
    Claremont Colleges Scholarship @ Claremont All HMC Faculty Publications and Research HMC Faculty Scholarship 8-1-2012 Consonance and Dissonance in Visual Music Bill Alves Harvey Mudd College Recommended Citation Bill Alves (2012). Consonance and Dissonance in Visual Music. Organised Sound, 17, pp 114-119 doi:10.1017/ S1355771812000039 This Article is brought to you for free and open access by the HMC Faculty Scholarship at Scholarship @ Claremont. It has been accepted for inclusion in All HMC Faculty Publications and Research by an authorized administrator of Scholarship @ Claremont. For more information, please contact [email protected]. Organised Sound http://journals.cambridge.org/OSO Additional services for Organised Sound: Email alerts: Click here Subscriptions: Click here Commercial reprints: Click here Terms of use : Click here Consonance and Dissonance in Visual Music Bill Alves Organised Sound / Volume 17 / Issue 02 / August 2012, pp 114 - 119 DOI: 10.1017/S1355771812000039, Published online: 19 July 2012 Link to this article: http://journals.cambridge.org/abstract_S1355771812000039 How to cite this article: Bill Alves (2012). Consonance and Dissonance in Visual Music. Organised Sound, 17, pp 114-119 doi:10.1017/ S1355771812000039 Request Permissions : Click here Downloaded from http://journals.cambridge.org/OSO, IP address: 134.173.130.244 on 24 Jul 2014 Consonance and Dissonance in Visual Music BILL ALVES Harvey Mudd College, The Claremont Colleges, 301 Platt Blvd, Claremont CA 91711 USA E-mail: [email protected] The concepts of consonance and dissonance broadly Plato found the harmony of the world in the Pythag- understood can provide structural models for creators of orean whole numbers and their ratios, abstract ideals visual music.
    [Show full text]
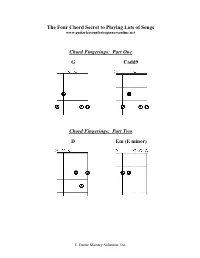
  • Part One G Cadd9 Chord Fingerings
    The Four Chord Secret to Playing Lots of Songs www.guitarlessonsforbeginnersonline.net Chord Fingerings: Part One G Cadd9 Chord Fingerings: Part Two D Em (E minor) © Guitar Mastery Solutions, Inc. Playing Chord Progressions A chord progression is a series of chords played one after the other. Most songs consist of several different chord progressions. Learning to play the chord progressions in this lesson will help you learn to play many different songs. Mastering the chord fingerings and chord progressions in this lesson will help you quickly learn to play many different songs in different styles of music. These fundamental chords are crucial to your development and improvement as a guitar player—learn them well and learn to change between them. You will use them for the rest of your guitar playing career! Chord Progression One Chords Used: D Cadd9 G Play four strums on each chord and change to the next: |D / / / |Cadd9 / / / |G / / / | (repeat) This chord progression is similar to the one used in the song “Can’t You See?” by the Marshall Tucker Band. Chord Progression Two Chords Used: D Cadd9 G This progression uses the same chords as the first one. The difference is that we will pick some of the notes in the first two chords and end with a strum on the final G chord. Key point to remember: Even though the pick hand is playing some single notes, your fret hand only needs to play the chord shapes, just like in Progression One. D Cadd9 G This chord progression and picking pattern is similar to the one used in the song “Sweet Home Alabama” by Lynyrd Skynyrd.
    [Show full text]