Principal Component Analysis on Soil Fertility Parameters in Vegetable Growing Locations of Kottayam District of Kerala
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Online Seat Allotment - 2021 Department of Education Administration of UT of Lakshadweep
Online Seat Allotment - 2021 Department of Education Administration of UT of Lakshadweep College Wise Balance Seats Course Name College Name Total Seats Available Seats Ayurveda Nurse (12 Months Directorate of Ayurveda Medical Education, Trivandrum 2 0 Diploma Course) Ayurveda Pharmacist (12 Months Directorate of Ayurveda Medical Education, Trivandrum 2 0 Diploma Course) Ayurveda Therapist (12 Months Directorate of Ayurveda Medical Education, Trivandrum 2 0 Diploma Course) Craftmanship (One year) Institute of Hotel Management Catering Technology & Applied 10 0 Nutrition, Chennai Diploma in Civil Engineering Directorate of Technical Education, Guindy, Chennai 3 0 Diploma in Civil Engineering Govt. Polytechnic College, Kalamassery 3 0 Diploma in Civil Engineering Govt. Polytechnic College, Kozhikode 3 0 Diploma in Civil Engineering Training Institute, Gujarat 1 0 Diploma in Electrical & Directorate of Technical Education, Guindy, Chennai 11 0 Electronics Diploma in Electrical & Govt. Polytechnic College, Kalamassery 2 0 Electronics Diploma in Electrical & Govt. Polytechnic College, Kozhikode 2 0 Electronics Diploma in Electronics & Directorate of Technical Education, Guindy, Chennai 3 0 Communication Diploma in Electronics Engg. Govt. Polytechnic, Kannur 2 0 Diploma in Mechanical Engg. Directorate of Technical Education, Guindy, Chennai 9 0 Diploma in Mechanical Engg. Govt. Polytechnic College, Kalamassery 3 0 Diploma in Mechanical Engg. Govt. Polytechnic College, Kozhikode 2 0 Diploma in Printing Technology Training Institute, Gujarat 1 1 Electronics & Instruments Directorate of Technical Education, Guindy, Chennai 5 0 Shore Mechanic Course (SMC) Central Institute of Fisheries Nautical and Engineering 22 0 Training (CIFNET), Chennai Stenographer & Secretarial Govt. ITI, Chalakkudi 1 0 Assistant (English) Surveyor Govt. ITI, Chalakkudi 2 0 Electronics Mechanic Govt. ITI, Kalamassery 1 0 Electronics Mechanic Govt. -

9 State Forest Management and Biodiversity: a Case of Kerala, India
9 State Forest Management and Biodiversity: A Case of Kerala, India Ellyn K. DAMAYANTI & MASUDA Misa 1. Introduction Republic of India is the seventh largest country in the world, covering an area of 3,287,263 km2.has large and diverse forest resources in 633,397 km2 of forest covers or 19.27% of land areas (ICFRE, 2003; FAO, 2003). Forest types in India vary from topical rainforest in northeastern India, to desert and thorn forests in Gujarat and Rajasthan; mangrove forests in West Bengal, Orissa and other coastal areas; and dry alpine forests in the western Himalaya. The most common forest types are tropical moist deciduous forest, tropical dry deciduous forests, and wet tropical evergreen forests. India has a large network of protected areas, including 89 national parks and around 497 wildlife sanctuaries (MoEF, 2005). India has long history in forest management. The first formal government approach to forest management can be traced to the enactment of the National Forest Policy of 1894, revised in 1952 and once again revised in 1988, which envisaged community involvement in the protection and regeneration of forest (MoEF, 2003). Even having large and diverse forest resources, India’s national goal is to have a minimum of one-third of the total land area of the country under forest or tree cover (MoEF, 1988). In management of state forests, the National Forest Policy, 1988 emphasizes schemes and projects, which interfere with forests that clothe slopes; catchments of rivers, lakes, and reservoirs, geologically unstable terrain and such other ecologically sensitive areas, should be severely restricted. -

Payment Locations - Muthoot
Payment Locations - Muthoot District Region Br.Code Branch Name Branch Address Branch Town Name Postel Code Branch Contact Number Royale Arcade Building, Kochalummoodu, ALLEPPEY KOZHENCHERY 4365 Kochalummoodu Mavelikkara 690570 +91-479-2358277 Kallimel P.O, Mavelikkara, Alappuzha District S. Devi building, kizhakkenada, puliyoor p.o, ALLEPPEY THIRUVALLA 4180 PULIYOOR chenganur, alappuzha dist, pin – 689510, CHENGANUR 689510 0479-2464433 kerala Kizhakkethalekal Building, Opp.Malankkara CHENGANNUR - ALLEPPEY THIRUVALLA 3777 Catholic Church, Mc Road,Chengannur, CHENGANNUR - HOSPITAL ROAD 689121 0479-2457077 HOSPITAL ROAD Alleppey Dist, Pin Code - 689121 Muthoot Finance Ltd, Akeril Puthenparambil ALLEPPEY THIRUVALLA 2672 MELPADAM MELPADAM 689627 479-2318545 Building ;Melpadam;Pincode- 689627 Kochumadam Building,Near Ksrtc Bus Stand, ALLEPPEY THIRUVALLA 2219 MAVELIKARA KSRTC MAVELIKARA KSRTC 689101 0469-2342656 Mavelikara-6890101 Thattarethu Buldg,Karakkad P.O,Chengannur, ALLEPPEY THIRUVALLA 1837 KARAKKAD KARAKKAD 689504 0479-2422687 Pin-689504 Kalluvilayil Bulg, Ennakkad P.O Alleppy,Pin- ALLEPPEY THIRUVALLA 1481 ENNAKKAD ENNAKKAD 689624 0479-2466886 689624 Himagiri Complex,Kallumala,Thekke Junction, ALLEPPEY THIRUVALLA 1228 KALLUMALA KALLUMALA 690101 0479-2344449 Mavelikkara-690101 CHERUKOLE Anugraha Complex, Near Subhananda ALLEPPEY THIRUVALLA 846 CHERUKOLE MAVELIKARA 690104 04793295897 MAVELIKARA Ashramam, Cherukole,Mavelikara, 690104 Oondamparampil O V Chacko Memorial ALLEPPEY THIRUVALLA 668 THIRUVANVANDOOR THIRUVANVANDOOR 689109 0479-2429349 -
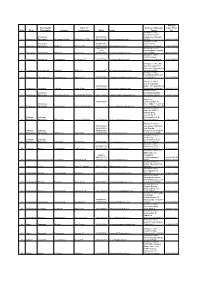
Sl.No. Block Panchayath/ Municipality Location Name of Entrepreneur Mobile E-Mail Address of Akshaya Centre Akshaya Centre Phone
Akshaya Panchayath/ Name of Address of Akshaya Centre Phone Sl.No. Block Municipality Location Entrepreneur Mobile E-mail Centre No Akshaya e centre, Chennadu Kavala, Erattupetta 9961985088, Erattupetta, Kottayam- 1 Erattupetta Municipality Chennadu Kavala Sajida Beevi. T.M 9447507691, [email protected] 686121 04822-275088 Akshaya e centre, Erattupetta 9446923406, Nadackal P O, 2 Erattupetta Municipality Hutha Jn. Shaheer PM 9847683049 [email protected] Erattupetta, Kottayam 04822-329714 9645104141 Akshaya E-Centre, Binu- Panackapplam,Plassnal 3 Erattupetta Thalappalam Pllasanal Beena C S 9605793000 [email protected] P O- 686579 04822-273323 Akshaya e-centre, Medical College, 4 Ettumanoor Arpookkara Panampalam Renjinimol P S 9961777515 [email protected] Arpookkara, Kottayam 0481-2594065 Akshaya e centre, Hill view Bldg.,Oppt. M G. University, Athirampuzha 5 Ettumanoor Athirampuzha Amalagiri Shibu K.V. 9446303157 [email protected] Kottayam-686562 0481-2730349 Akshaya e-centre, , Thavalkkuzhy,Ettumano 6 Ettumanoor Athirampuzha Thavalakuzhy Josemon T J 9947107199 [email protected] or P.O-686631 0418-2536494 Akshaya e-centre, Near Cherpumkal 9539086448 Bridge, Cherpumkal P O, 7 Ettumanoor Aymanam Valliyad Nisha Sham 9544670426 [email protected] Kumarakom, Kottayam 0481-2523340 Akshaya Centre, Ettumanoor Municipality Building, 8 Ettumanoor Muncipality Ettumanoor Town Reeba Maria Thomas 9447779242 [email protected] Ettumanoor-686631 0481-2535262 Akshaya e- 9605025039 Centre,Munduvelil Ettumanoor -

Kottayam District
KOTTAYAM DISTRICT Centre for Water Resources Development and Management Endline Evaluation of PMKSY-WDC watershed projects Endline Evaluation of PMKSY-WDC Watershed Projects REPORT: ERATTUPETTA BLOCK (Kottayam District) The IWMP project area lies in the Erattupetta Block Panchayath which is 38 km away from the district HQ in the Meenchil Taluk of Kottayam District. The project area, lying in the catchment of Meenachil River, consists of seven micro watersheds namely Orappurakkad, Vellani, Areekkathodu, Vengattuthodu, Mesthiripadi, Nedungazhi and Maravikallu, covering Teekoy, Thalanad, Melukavu, Moonilavu, Erattupetta and Poonjar Gram Panchayaths. The total treatable area of the project is 5365 ha. Table 1 Details of micro watersheds in the project area Sl Gram Treatable Code Name Geographical Cordinates No Panchayath Area (Ha) 76˚45'46.328"E 76˚47'8.784"E 1 12M 25m Orappurakkad Teekoy 650 9˚44'49.791"N 9˚46'26.11"N 76˚50'23.987"E 76˚51'44.717"E 2 12M25k Vellani Thalanadu 568 9˚42'29.466"N 9˚44'41.738"N 76˚45'46.328"E 76˚47'8.784"E Melukavu & 3 12m25d Areekkathodu 463 9˚44'49.791"N 9˚46'26.11"N Moonilavu 76˚46'5.708"E 76˚47'50.378"E 4 12M25g Vengattuthodu Moonilavu 820 9˚42'34.675"N 9˚45'11.264"N 76˚48'56.255"E 76˚49'56.027"E 5 12M25i Mesthiripadi Thalanadu 231 9˚41'55.209"N 9˚43'36.007"N Teekoy, 76˚46'55.731"E 76˚52'45.229"E 6 12M25n Nedungazhi Erattupetta, 1897 9˚40'41.483"N 9˚42'42.519"N Poonjar 76˚47'10.117"E 76˚49'32.556"E Thalanadu & 7 12M25h Maravikallu 736 9˚41'55.172"N 9˚43'43.68"N Teekoy Total 5365 139 Centre for Water Resources Development and Management Endline Evaluation of PMKSY-WDC watershed projects Figure 1 Location map of the project area The evaluation team from CWRDM visited the project area on 14/03/2019. -
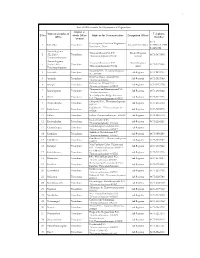
List of Offices Under the Department of Registration
1 List of Offices under the Department of Registration District in Name& Location of Telephone Sl No which Office Address for Communication Designated Officer Office Number located 0471- O/o Inspector General of Registration, 1 IGR office Trivandrum Administrative officer 2472110/247211 Vanchiyoor, Tvpm 8/2474782 District Registrar Transport Bhavan,Fort P.O District Registrar 2 (GL)Office, Trivandrum 0471-2471868 Thiruvananthapuram-695023 General Thiruvananthapuram District Registrar Transport Bhavan,Fort P.O District Registrar 3 (Audit) Office, Trivandrum 0471-2471869 Thiruvananthapuram-695024 Audit Thiruvananthapuram Amaravila P.O , Thiruvananthapuram 4 Amaravila Trivandrum Sub Registrar 0471-2234399 Pin -695122 Near Post Office, Aryanad P.O., 5 Aryanadu Trivandrum Sub Registrar 0472-2851940 Thiruvananthapuram Kacherry Jn., Attingal P.O. , 6 Attingal Trivandrum Sub Registrar 0470-2623320 Thiruvananthapuram- 695101 Thenpamuttam,BalaramapuramP.O., 7 Balaramapuram Trivandrum Sub Registrar 0471-2403022 Thiruvananthapuram Near Killippalam Bridge, Karamana 8 Chalai Trivandrum Sub Registrar 0471-2345473 P.O. Thiruvananthapuram -695002 Chirayinkil P.O., Thiruvananthapuram - 9 Chirayinkeezhu Trivandrum Sub Registrar 0470-2645060 695304 Kadakkavoor, Thiruvananthapuram - 10 Kadakkavoor Trivandrum Sub Registrar 0470-2658570 695306 11 Kallara Trivandrum Kallara, Thiruvananthapuram -695608 Sub Registrar 0472-2860140 Kanjiramkulam P.O., 12 Kanjiramkulam Trivandrum Sub Registrar 0471-2264143 Thiruvananthapuram- 695524 Kanyakulangara,Vembayam P.O. 13 -
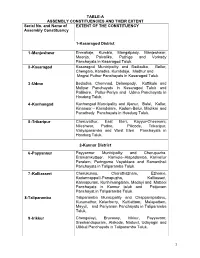
List of Lacs with Local Body Segments (PDF
TABLE-A ASSEMBLY CONSTITUENCIES AND THEIR EXTENT Serial No. and Name of EXTENT OF THE CONSTITUENCY Assembly Constituency 1-Kasaragod District 1 -Manjeshwar Enmakaje, Kumbla, Mangalpady, Manjeshwar, Meenja, Paivalike, Puthige and Vorkady Panchayats in Kasaragod Taluk. 2 -Kasaragod Kasaragod Municipality and Badiadka, Bellur, Chengala, Karadka, Kumbdaje, Madhur and Mogral Puthur Panchayats in Kasaragod Taluk. 3 -Udma Bedadka, Chemnad, Delampady, Kuttikole and Muliyar Panchayats in Kasaragod Taluk and Pallikere, Pullur-Periya and Udma Panchayats in Hosdurg Taluk. 4 -Kanhangad Kanhangad Muncipality and Ajanur, Balal, Kallar, Kinanoor – Karindalam, Kodom-Belur, Madikai and Panathady Panchayats in Hosdurg Taluk. 5 -Trikaripur Cheruvathur, East Eleri, Kayyur-Cheemeni, Nileshwar, Padne, Pilicode, Trikaripur, Valiyaparamba and West Eleri Panchayats in Hosdurg Taluk. 2-Kannur District 6 -Payyannur Payyannur Municipality and Cherupuzha, Eramamkuttoor, Kankole–Alapadamba, Karivellur Peralam, Peringome Vayakkara and Ramanthali Panchayats in Taliparamba Taluk. 7 -Kalliasseri Cherukunnu, Cheruthazham, Ezhome, Kadannappalli-Panapuzha, Kalliasseri, Kannapuram, Kunhimangalam, Madayi and Mattool Panchayats in Kannur taluk and Pattuvam Panchayat in Taliparamba Taluk. 8-Taliparamba Taliparamba Municipality and Chapparapadavu, Kurumathur, Kolacherry, Kuttiattoor, Malapattam, Mayyil, and Pariyaram Panchayats in Taliparamba Taluk. 9 -Irikkur Chengalayi, Eruvassy, Irikkur, Payyavoor, Sreekandapuram, Alakode, Naduvil, Udayagiri and Ulikkal Panchayats in Taliparamba -

Mahatma Gandhi University, Kottayam, Kerala – 686560
MAHATMA GANDHI UNIVERSITY, KOTTAYAM, KERALA – 686560 DETAILS OF WORKS PERFORMED IN EACH SECTION OF THE UNIVERSITY Supervisory Officers Section Contact Sl. No. Name of Section Dealing works in the Section E-Mail ID Deputy Number Assistant Registrar Registrar ADMINISTRATION Service matters of Staff: 1. AD A I 0481-2733280 [email protected] JR/DR/AR/SO/Assistants Service Matters of: OA/Clerical Asst./Sto re Asst./Staff Nurse/Roneo Operator/Lab Techn 2. AD A III 0481-2733302 [email protected] (health centre)/Tele. Operator GO Endorsement, Part Time Sweeper engagement Service Matters – FC&D, Drivers, Engineers, Computer Programmers, Security Personal, Anti 3. AD A IV 0481-2733303 [email protected] Harassment Cell, Sanctioning of leave to SO & Above officers AR I (Admn) DR I (Admn) Pension: Bill preparation, Pension certificate 0481-2733239 0481-2733226 4. AD A VIII 0481-27733420 [email protected] issue, Income Tax matters of pensioners Pension Calculation, Pension Sanctioning, NLC [email protected] 5. AD A X Issuing, Family pension, VRS, Restoration of 0481-2333420 commuted portion of pensioners 6. AD A VI Medical Reimbursement 0481-2733305 [email protected] 7. Records Keeping University Records 0481-2733412 DR III All administrative matters related to Inter AR V (Admn) 8. AD A VII 0481-2733425 [email protected] (ADMN) University / Inter School Centres 0481-273 0481-273 3608 Service matters of VC, PVC, Registrar, FO, and [email protected] AR II (Admn.) DR II (Admn) 9. Ad A II 0481-2733281 CE. 0481-2733240 0481-2733227 1 Supervisory Officers Section Contact Sl. -

Puthuppally Assembly Kerala Factbook
Editor & Director Dr. R.K. Thukral Research Editor Dr. Shafeeq Rahman Compiled, Researched and Published by Datanet India Pvt. Ltd. D-100, 1st Floor, Okhla Industrial Area, Phase-I, New Delhi- 110020. Ph.: 91-11- 43580781, 26810964-65-66 Email : [email protected] Website : www.electionsinindia.com Online Book Store : www.datanetindia-ebooks.com Report No. : AFB/KR-098-0619 ISBN : 978-93-5313-599-7 First Edition : January, 2018 Third Updated Edition : June, 2019 Price : Rs. 11500/- US$ 310 © Datanet India Pvt. Ltd. All rights reserved. No part of this book may be reproduced, stored in a retrieval system or transmitted in any form or by any means, mechanical photocopying, photographing, scanning, recording or otherwise without the prior written permission of the publisher. Please refer to Disclaimer at page no. 130 for the use of this publication. Printed in India No. Particulars Page No. Introduction 1 Assembly Constituency -(Vidhan Sabha) at a Glance | Features of Assembly 1-2 as per Delimitation Commission of India (2008) Location and Political Maps Location Map | Boundaries of Assembly Constituency -(Vidhan Sabha) in 2 District | Boundaries of Assembly Constituency under Parliamentary 3-9 Constituency -(Lok Sabha) | Town & Village-wise Winner Parties- 2019, 2016, 2014, 2011 and 2009 Administrative Setup 3 District | Sub-district | Towns | Villages | Inhabited Villages | Uninhabited 10-11 Villages | Village Panchayat | Intermediate Panchayat Demographics 4 Population | Households | Rural/Urban Population | Towns and Villages -

STATE BANK of TRAVANCORE.Pdf
STATE DISTRICT BRANCH ADDRESS CENTRE IFSC CONTACT1 CONTACT2 PB 14, Opp V V Mahal Theatre, ANDHRA Mosque Rd PRADESH CHITTOOR tirupathy Tirupathi TIRUPATI SBTR0000649Tirupathi [email protected] 1st Lane, gunturvarithot ANDHRA a, Guntur PRADESH GUNTUR guntur Guntur GUNTUR SBTR0000625522001 [email protected] SRINIVASA NAGAR AS RAO COLONY AS NAGAR RAO NAGAR ANDHRA SECUNDERA SECUNDERA PRADESH HYDERABAD BADD BAD HYDERABAD SBTR0001151040-27810013 022-27564755 VARMA HEIGHTS, 16- 11-511/D/15, ROAD NO 9, SHALIVAHAN A NAGAR, ANDHRA DILSUKH HYDERABAD PRADESH HYDERABAD NAGAR 500060 HYDERABAD SBTR0001202040-29801361 Shri. K. Chellappa Chief Pb No 21, Manager PH Kushal 040-24744880 Chambers, Shri. Bank Street, Gummadi Koti, Sathish Babu ANDHRA Hyderabad Manager PH PRADESH HYDERABAD Hyderabad 500 001 HYDERABAD SBTR0000264040-24654686 MIG 155, KPR COMPLEX, ROAD NO.1,PHASE I & II, KPHB COLONY, KUKATPALLY, ANDHRA KUKATPALLY, HYDERABAD PRADESH HYDERABAD HYDERABAD 500 072 HYDERABAD SBTR0000743040-23051689 2nd FLOOR, KAMALA TOWERS SP ROAD, MICCORPOR SECUNDERA ATE BAD 500003 ANDHRA BRANCH, mcbhyd@sbt. PRADESH HYDERABAD HYDERABAD co.in HYDERABAD SBTR0001111040-2780013 HOUSE NO.6-1-276, FLAT NO.101A, ARCHANA BLOCK, CONJEEVAR AM HOUSE, PADMARAO PADMARAO NAGAR, ANDHRA NAGAR, SECUNDERA PRADESH HYDERABAD HYDERABAD BAD TARNAKA SBTR0000811040-27501689 040-27501690 H No.8-2- 293/82/L/247/ a/a, MLA PSB, Colony, HYDERABAD Banjara Hills, ANDHRA -BANJARA Hyderabad PRADESH HYDERABAD HILLS 500034 HYDERABAD SBTR0000987022-27564754 RETAIL SAI VAMSEE, ASSETS PLOT 645, CENTRAL -

Academic Counsellors: E-Mail & Mobile Numbers RC 14
ACD_CD ACD_NM ACD_ADDRESS EMAILID ACD_MOBILE RC_CD SC_CD COURSE MADHU VILLA POOZHIKOL P.O. DEVMT:BHC12, DEVMT:BHC13, DEVMT:BHC14, 141172960 RADHIKA P C [email protected] 9995882584 14 1402 KADUTHURUTHY,KOTTAYAM-682013 DEVMT:BHCL11, DEVMT:BHCP11 KOTTAKKAL PUTHENPURA MADOM MAH:MHI1, MAH:MHI2, MAH:MHI3, MAH:MHI4, 141116960 B.SHYAMA 9495368688 14 14000 KOONAMMZVU P.O ERNAKULAM-683518 MAH:MHI5, MAH:MHI8 CHAKKACHAM 141116720 Ms.SHINY K.A VEEDU,KOKOTHAMANGALAM P.O 9446000957 14 14180D CHBHC:CNSHC1, CHBHC:CNSHCP1 CHERTHALA ALAPPUZHA-688527 Kunnanchathanattu House Poochakal Via 1463610 Vijay Kumar K 9895814131 14 14157 BA:BSHF101, MP:MS3, MP:MS8, MP:MS9 Cherthala ARANHIKKAL HOUSE NEAR MUTTOM JUMA 14243400 A.ABOOBACKER MASJID THAIKKATTUKARA P.O. ALUVA 9447174245 14 1400 CAL:BAL1, CAL:BAL2 683106 33/3198 AZHIKKAKATH HOUSE 1464502 A.C.JOSEPH 9447414291 14 14159 DFPT:BPVI42, DFPT:BPVI43 MANAIKKAPARAMB VENNALA 682029 1425369 A.J.JOSE NEWMAN COLLEGE THODUPUZHA 685585 14 1408 MEG:MEG10, MEG:MEG11, MEG:MEG3 P S M O COLLEGE TIRURANGADI P O 1422580 ABDUL AZEEZ M 9847191079 14 1409 BA:EEC11, BA:EEC19 MALAPPURAM 676306 PSMO COLLEGE TIRURANGADI PO 14388840 ABDUL BARI C 14 1409 CFE:BEG4, CFE:BEG5, CFE:BEG6 MALAPPURAM PSMO COLLEGE, TIRURANGADI PO, BA:BEGE101, BA:BEGE102, BA:BEGE103, BA:BEGE104, 14339160 ABDUL BARI C 14 1409 MALAPPURAM BA:BEGE105 CHALIYATHODIKA HOUSE KATTUMUNDA 1442820 ABDUL GAFAR C 9388827390 14 14122 BA:BEGE105, BA:EEG3, BA:EEG4 P.O. NADUVATH MALAPPURAM P S M O COLLEGE TIRURANGADI P O 1422484 ABDUL KARIM C 9847961831 14 1409 BCOM:ECO1, BCOM:ECO13, BCOM:ECO3 MALAPPURAM 676306 PSMO COLLEGE, TIRURANGADI PO, 14339100 ABDUL NASAR V 14 1409 BCOM:ECO10, BCOM:ECO14 MALAPPURAM PSMO COLLEGE TIRURANGADI PO 14339280 ABDUL SAMAD 14 1409 BA:BEGE101, BA:BEGE102, BA:FEG1, BA:FEG2 MALAPPURAM THODUMMANI KIZHETHIL HOUSE MSCCFT:MCFT4, MSCCFT:MCFTL8, MSCCFT:MCFTP1, 1435240 ABDUL SHUKOOR TK PERINTHATTIRI P.O. -

Certain Student Centric Methods Used for Enhancing Learning Experiences
2.3.1 Student centric methods, such as experiential learning, participative learning and problem solving methodologies are used for enhancing learning experiences CERTAIN STUDENT CENTRIC METHODS USED FOR ENHANCING LEARNING EXPERIENCES Contents Entrepreneurship Development Club 4 Quiz Club 19 National Science Day 26 Music Club 48 Scholar Support Programme 52 Walk With a Scholar 58 Energy and Environment Club 66 Department of English 70 Peer Teaching . 70 English Speaking Corner . 73 Department of Vocational Education 75 Food Fest 2018 . 75 Rice Cultivation by Students . 79 ROn Farm VAM Production . 82 Agri Fest 2017 . 85 Department of Mathematics 90 Guidance and Counseling . 90 Prof. Mathew T. Matheikal Intercollegiate Mathematics Quiz Competition . 90 Department of Statistics 117 Ramakrishna Pillai Memorial All Kerala Problem Solving Contest in Statistics 117 Department of Physics 125 Department of Chemistry 128 Report of Student Centric Methods . 128 Infotainment Fest - ATMOS2k18 . 131 Science Popularization Campign . 133 2 Department of Botany 135 Plants diversity survey in Granite quarry site . 135 Department of Zoology 140 Department of Economics 142 Department of Hindi 144 3 Entrepreneurship Development Club 4 Entrepreneurship Development Club Report of the Activities 2016-17 The purpose of Entrepreneurship Development (ED) Club in our college is to develop entrepreneurial capacities and mind sets in our students. It tries to fulfil its mission through: Identification of opportunities for self-employment, Augmenting entrepreneurship among students through training, and Inculcating the spirit of 'Entrepreneurship' in youth. Creation of Media Hub As part of the All India Inter University Men Volley ball championship 2016-17, the Media and Publicity Committee selected by the Principal, felt a need for a media team to facilitate news reporting, capturing photographs, video recording etc.