Computer Mathematical Models in Belaying Techniques
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2. the Climbing Gym Industry and Oslo Klatresenter As
Norwegian School of Economics Bergen, Spring 2021 Valuation of Oslo Klatresenter AS A fundamental analysis of a Norwegian climbing gym company Kristoffer Arne Adolfsen Supervisor: Tommy Stamland Master thesis, Economics and Business Administration, Financial Economics NORWEGIAN SCHOOL OF ECONOMICS This thesis was written as a part of the Master of Science in Economics and Business Administration at NHH. Please note that neither the institution nor the examiners are responsible − through the approval of this thesis − for the theories and methods used, or results and conclusions drawn in this work. 2 Abstract The main goal of this master thesis is to estimate the intrinsic value of one share in Oslo Klatresenter AS as of the 2nd of May 2021. The fundamental valuation technique of adjusted present value was selected as the preferred valuation method. In addition, a relative valuation was performed to supplement the primary fundamental valuation. This thesis found that the climbing gym market in Oslo is likely to enjoy a significant growth rate in the coming years, with a forecasted compound annual growth rate (CAGR) in sales volume of 6,76% from 2019 to 2033. From there, the market growth rate is assumed to have reached a steady-state of 3,50%. The period, however, starts with a reduced market size in 2020 and an expected low growth rate from 2020 to 2021 because of the Covid-19 pandemic. Based on this and an assumed new competing climbing gym opening at the beginning of 2026, OKS AS revenue is forecasted to grow with a CAGR of 4,60% from 2019 to 2033. -

Kitsap Basic Climbing
! KITSAP MOUNTAINEERS BASIC CLIMBING COURSE Class 4 and Field Trips 4 & 5 BASIC CLIMBING - CLASS #4 ROCK CLIMBING Class #4 Topics Rock Climbing Process Rock Climbing Techniques Anchors Field Trip Leader Q & A (Field Trip 4) Assigned Reading (complete prior to Class #4) Assigned Reading: Freedom Of The Hills Subject Alpine Rock Climbing ...............................................................Ch 12 Basic Climbing Course Manual All Class #4 Material Additional Resources Find a good book on stretching exercises—it is helpful to loosen up before rock climbing. ROPED CLIMBING OVERVIEW Roped climbing involves the leader and follower(s) attached to a rope for protection as they ascend and descend, so that in the event of a fall the rope can be used to catch the falling climber. In basic rock climbing, the leader is tied into one end of a rope and the follower (second) into the other end. The follower may also attach to a “ground anchor” and will prepare to belay the leader by feeding the rope through his/her belay device. When the follower (belayer) is ready (follower yells: “BELAY ON”), the leader ascends a section of rock (leader: “CLIMBING”, follower: “CLIMB”) while placing protection gear and connecting the climbing rope to the protection as he/she climbs upward. In event of a fall (leader: “FALLING!”), the belayer stops the fall by “braking” the rope at the belay device, and tightening the rope through the protections. When the leader has reached the top of the section (pitch), the leader sets up an anchor and attaches him/ her. The leader tells the follower to take him/her off belay (leader: “OFF BELAY”). -

Belaying » Get It Right!
BeLaYing » get it right! British Mountaineering Council Working for Climbers, hill Walkers and Mountaineers CheCk Harness CheCk KnOT CheCk BeLaY PAY aTTENTiOn! KnOw how to use your gear there are many different ropes and belaying devices available. read and understand the manufacturer’s instructions. if still unsure, get advice from someone more experienced. never belay with equipment you do not know how to use. COnTrol the rOpe Belaying is a complex skill requiring practice and experience to become competent. inattentive belaying is the cause of many preventable climbing accidents. Mistakes can result in serious injuries for climber, belayer or both. Check both climber’s knot and belay device before starting a climb. ensure your rope is long enough for your climb. if in doubt knot the free rope end. Pay attention and keep a controlling hand on the rope. geT in the BesT pOsiTiOn Anticipate the direction of pull, and position yourself appropriately. if you stand near the foot of a climb you are less likely to be pulled off balance when holding a fall or lowering a climber. if there is a lot of rope paid out the climber could hit the ground. Standing near the climb results in less rope between belayer and climber. When the climber is not moving, hold the rope in the locked position. suppOrT BriTisH CLiMBing – jOin THe BMC TOdaY: WWW.THeBMC.Co.uk T: 0161 445 6111 Belay deviCe deSign there are two types of belay device: manual devices and assisted braking devices. A manual device employs mainly friction, allowing some rope slippage when holding a fall. -

California— Yosemite
California— Yosemite: (1) On October 25, 1952 a party composed of Bill Long, Dick Long, A l Steck and William Dunmire (22) set out to attempt an ascent of the El Capitan Buttress (east of the main face). Steck and Dunmire were the first rope of two, and on the third pitch it was Dunmire’s turn to lead. Steck, belaying from a four foot wide ledge, was anchored to a piton and had placed another piton through which he belayed Dunmire. The route led up alongside a vertical crack into which Dunmire placed two pitons, about 6 feet apart. Along this crack was a large block which appar ently was not a part of the cliff but wedged in on one side and the pitons tested soundly, and he felt he had no real reason to doubt their security. Another higher crack failed to be satisfactory for piton use. A spade piton, however, was placed under a somewhat rotten flake. This also was tested. Dunmire warned Steck that the top piton was not too sound. He used it for direct aid to gain a small foothold three feet above. At this point, three feet above the highest piton, twelve feet above the next and and about twenty feet above the belayer, he attempted to place a fourth piton at arms length above him in a horizontal crack under an overhang. While he was hammering his feet slipped and he fell. He fell nearly free, striking the cliff only once and landed on his shoulder and head on a ledge about 15 feet below Steck. -

Belaying the Leader
A4 - BELAYING THE LEADER Belaying the leader involves paying out rope through the belay device to the leader (A), holding the rope in case of a fall and then lowering the leader back to the ground once she has climbed the route. This lets the leader climb the route in safety. To belay well, the belayer (B) should: A • be able to use the belay device properly; • belay themselves to the ground/nearby crag if they are much lighter than the leader (A) or if there is a risk of them falling off an exposed ledge from which they are belaying; B • pay constant attention to the leader (A) as she climbs and stand as close in as possible to the rock; • never let go of the free end of the rope; • not pay out to the climber (A) more rope than is necessary and be ready to take-in slack rapidly if needed; • be ready to hold the companion (A) is she falls and lower her to the ground as indicated in the instructions of the belay device used. When sport climbing it is common to use a belay device with assisted braking to belay the leader. Belay devices with assisted braking are popular because, in the case of a fall, they automatically lock the rope provided the free end of the rope is held. The devices currently on the market do not always work perfectly in the following situations: • paying out rope quickly to the leader without the rope jamming; • they are dangerous if the rope is inserted incorrectly. -

Abseil Handbook Web Version
THE ABSEILING HANDBOOK ABSEILING HANDBOOK Abseiling is a lot of fun and may offer an experience of exhilaration, personal challenge or adrenalin rush. However, abseiling is not really a “stand alone” activity, but rather a skill that is employed in the sports of rock climbing, canyoning, caving and mountaineering, so go on and try all the rock related activities. Abseilers need to be aware that it is an activity where serious injury or death can occur as a result of; Falling off a cliff. Falling rocks. Equipment dropped by others. Failure of anchors or equipment Misuse of equipment. These risks are minimised by abseiling activities being lead by qualified persons, and by training all persons participating in an abseil activity in cliff top safety, use and care of equipment and standard calls, prior to the activity. Therefore, to become proficient in abseiling requires more than reading the information contained in this handbook, which is only intended as a learning aid to be used in conjunction with proper instruction. To become proficient requires undertaking a basic rock-craft course in the first instance, followed by regular practice under varying conditions. All persons have the responsibility for taking care of their personal safety as well as that of others. This handbook has been prepared by “Fred” Bernard Kaltenbacher Activity Leader Greater Western Sydney Region and is intended for use by Scouts for Scouts THE WAY THINGS WERE The ‘Absyle’ is used for rock work, generally for descending though it can be used of some faces for ascent. In the ‘Absyle’ the body is upright but the legs are stretched out, and the feet pressed against the rock face. -

Rock Climbing Fundamentals Has Been Crafted Exclusively For
Disclaimer Rock climbing is an inherently dangerous activity; severe injury or death can occur. The content in this eBook is not a substitute to learning from a professional. Moja Outdoors, Inc. and Pacific Edge Climbing Gym may not be held responsible for any injury or death that might occur upon reading this material. Copyright © 2016 Moja Outdoors, Inc. You are free to share this PDF. Unless credited otherwise, photographs are property of Michael Lim. Other images are from online sources that allow for commercial use with attribution provided. 2 About Words: Sander DiAngelis Images: Michael Lim, @murkytimes This copy of Rock Climbing Fundamentals has been crafted exclusively for: Pacific Edge Climbing Gym Santa Cruz, California 3 Table of Contents 1. A Brief History of Climbing 2. Styles of Climbing 3. An Overview of Climbing Gear 4. Introduction to Common Climbing Holds 5. Basic Technique for New Climbers 6. Belaying Fundamentals 7. Climbing Grades, Explained 8. General Tips and Advice for New Climbers 9. Your Responsibility as a Climber 10.A Simplified Climbing Glossary 11.Useful Bonus Materials More topics at mojagear.com/content 4 Michael Lim 5 A Brief History of Climbing Prior to the evolution of modern rock climbing, the most daring ambitions revolved around peak-bagging in alpine terrain. The concept of climbing a rock face, not necessarily reaching the top of the mountain, was a foreign concept that seemed trivial by comparison. However, by the late 1800s, rock climbing began to evolve into its very own sport. There are 3 areas credited as the birthplace of rock climbing: 1. -

Rock Climbing Equipment - 10 Min (C) Rock Climbing Techniques - 10 Min (D) Safety Tips - 10 Min (E) Conclusion - 05 Min
SER CONTENT No LESSON PLAN LESSON PLAN : ADV 3 ROCK CLIMBING Period - Five Type - Lecture -1 / Demo/Practice - 4 Code - ADV 3 Term - II / III (SD/SW) ______________________________________________________________ Training Aids 1. Computer Slides, Charts, Pointer, Black board & Chalk. Time Plan 2. (a) Introduction - 05 Min (b) Rock Climbing Equipment - 10 Min (c) Rock Climbing Techniques - 10 Min (d) Safety Tips - 10 Min (e) Conclusion - 05 Min INTRODUCTION. 3. Rock climbing is an activity in which participants climb up, down or across natural rock formations or artificial rock walls. The goal is to reach the summit of a formation or the endpoint of a pre-defined route without falling. Rock climbing competitions have objectives of completing the route in the quickest possible time or the farthest along an increasingly difficult route. AIM. 4. To acquaint NCC cadets with Rock Climbing as a part of Adventure training. PREVIEW. 5. The lecture will be conducted in following parts :- (a) Part I - Rock Climbing Equipment. (b) Part II - Rock Climbing Techniques. (c) Part III - Safety Tips. (a) PART I : ROCK CLIMBING EQUIPMENT 8. A Wide Range of Equipment Is Used During Rock Climbing. They are as follows :- (a) Rope and Webbing. Ropes used for climbing can be divided into two classes:- (i) Dynamic Ropes. These are designed to absorb the energy of a falling climber, and are usually used as Belaying ropes. When a climber falls, the rope stretches, reducing the maximum force experienced by the climber, their belayer. (ii) Low Elongation Ropes. Low elongation ropes are also called static ropes which stretch much less, and are usually used in anchoring systems. -
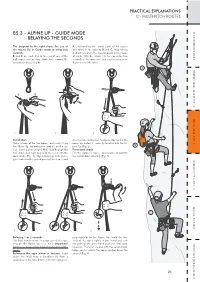
Alpine up - Guide Mode Belaying the Seconds
PRACTICAL EXPLANATIONS B - MULTI-PITCH ROUTES B5.3 - ALPINE UP - GUIDE MODE BELAYING THE SECONDS The diagram to the right shows the use of A is belayed to the central point of the stance the Alpine Up in Guide mode to belay two and takes in the rope to B and C, maintaining seconds: a slight tension in the rope to avoid giving loops B and C are each tied to the end of one of the of slack. With the Alpine Up he can belay two half ropes and as they climb they remove the seconds at the same time and each second is in- EXPLANATIONS PRACTICAL quickdraws placed by A. dependent of the other. A STOP! 1 2 OK! A - SINGLE-PITCH SPORT CLIMBING SPORT A - SINGLE-PITCH 1 2 3 Installation. into the hole marked of the Alpine Up, so that the Make a loop of the two ropes and insert it into ropes are below it, correctly inserted into the Al- ROUTES B - MULTI-PITCH the Alpine Up, following the symbols on the de- pine Up (Fig. 2). B vice. Insert a pear-shaped HMS krab through the Functional check. hole marked,at right angles to the lever, with the Pull the climber’s ropes downwards, to confirm rope inside (Fig. 1). Clip a Concept SGL screw- the system locks correctly (Fig. 3). gate krab into the central point of the stance and A C - CLIMBING A VIA FERRATA C 4 5 6 TECHNICAL FEATURES Belaying 1 or 2 seconds. perpendicular to the Alpine Up. Hold the free Use both hands to take in progressively the rope ends of the ropes tightly in one hand and with through the Alpine Up (Fig. -

Inspire Rock Lead Climbing/Belaying Standards
inSPIRE Rock Lead Climbing/Belaying Standards All climbing is dangerous; lead climbing, particularly so. The dangers involved with lead climbing affect not only you and your partner but also those around you. Because our goal is to set and maintain the highest standards safety for all gym guests and staff, we must require and enforce strict adherence to our lead climb/belay standards. These standards and practices may differ from what you do at other gyms or outside; these standards are particular to inSPIRE Rock. Remember lead climbing (or any climbing) at inSPIRE Rock is a privilege not a right; consistent or gross disregard for our standards will result in the loss of that privilege. Belaying is restricted to those 14 years of age or older. Standards – Equipment: Lead climber/belayers are required to use a UIAA/CE certified sit type harness with a belay loop that is less than 5 years old and does not show excessive wear. UIAA/CE approved belay devices must be used. These devices must be in good working order and not show signs of excessive wear. Stitch plates, plate type plaquette devices (e.g. Kong Gi Gi, and figure 8 devices) are not permitted. Belay carabiners must be UIAA/CE approved HMS/Pear-shaped locking carabiners, which are free from excessive wear and in good working order. Lead ropes are provided by inSPIRE Rock, however you may elect to use your own rope. Only UIAA certified dynamic single ropes are allowed. Ropes must be less than 5 years old, regularly inspected and have a known history. -

Belay Device Theory, Testing and Practice Theory
Belay Device Theory, Testing and Practice by Jim Titt 30 Jan 2009 Downloaded from www.bolt-products.com The following work was part of a project done to gain a better understanding of how belay devices work and to see how they could be improved. The copyright to all the original parts of this work are property of Bolt Products, Germany. All or any parts of this study may only be reproduced if copyright credit is given to Bolt Products. Germany. Belay plates are sad, neglected things, there are more studies on rope characteristics and impact forces than one can possibly imagine while the object that controls these forces is hardly ever examined or even considered. Some tests have been performed and the results vary from useful through helpful to criminally irresponsible with some woeful knowledge of basic physics and material science often being displayed. The only really useful theoretical work on how belay devices work was done by Attaway but even he suffered from some simplification and the failure to fully appreciate the importance of the rope itself. The best practical tests on various belay devices are those by S. Ratzenburger and the DAV (German Alpine Association). While many will wish to leave out the theory section with its implication of heavy duty mathematics this would be a mistake, without at least skimming it to get the concepts the rest of this work will probably be meaningless. For independent comparison tests of a variety of belay devices see the bibliography attatched. Theory The Braking Force(s) To the casual user it appears there are as many as three forces acting in a belay device to provide the necessary resistance. -

Top Rope Climbing Handbook
Top Rope Climbing Handbook Contents 1. What to expect 2. Equipment 3. Knots 4. Positions and equipment used by the climbing team 5. How the climbing session runs 6. Ascending the wall 7. Descending the wall 8. Helpful tips for a successful climbing session 19/11/2015 Climbing Handbook Daradgee Environmental Education Centre Top Rope Climbing at Daradgee At the Daradgee Environmental Education Centre we encourage accompanying adults to become involved in all activities. By training as a belay you can ensure the optimal student outcomes for the climbing sessions. This includes: Developing and applying challenging, new skills. Maximising climber participation by operating more climbing stations. Helping climbers develop their personal and social capabilities and physical skills through challenge Bouldering introduces climbers to safe and supportive 1. What to expect climbing technique. Before the session BOULDERING: Where practical, all climbers (& adults) will participate in a Bouldering session. Bouldering is climbing up to 2.4 metres and does not require a harness and belay. The Bouldering session is an experience where climbing technique is developed and everyone can become familiar with the climbing wall. THIS HANDBOOK must be read to fulfil your preparatory requirements for the climbing session. Additionally, teachers are required to read relevant CARA’s and ensure all climbers have provided written informed consent through the Climbing Permission Letter. TOP ROPE CLIMBING BELAY TRAINING - The Daradgee instructor will lead a Belay Training Induction. It is your instructor’s job to ensure you are prepared for the session and to oversee all operations in the climbing shed. Our aim is for the belay team to be confident and competent with their job.