Topological Data Analysis with Metric Learning and an Application to High-Dimensional Football Data
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Who Can Replace Xavi? a Passing Motif Analysis of Football Players
Who can replace Xavi? A passing motif analysis of football players. Javier Lopez´ Pena˜ ∗ Raul´ Sanchez´ Navarro y Abstract level of passing sequences distributions (cf [6,9,13]), by studying passing networks [3, 4, 8], or from a dy- Traditionally, most of football statistical and media namic perspective studying game flow [2], or pass- coverage has been focused almost exclusively on goals ing flow motifs at the team level [5], where passing and (ocassionally) shots. However, most of the dura- flow motifs (developed following [10]) were satis- tion of a football game is spent away from the boxes, factorily proven by Gyarmati, Kwak and Rodr´ıguez passing the ball around. The way teams pass the to set appart passing style from football teams from ball around is the most characteristic measurement of randomized networks. what a team’s “unique style” is. In the present work In the present work we ellaborate on [5] by ex- we analyse passing sequences at the player level, us- tending the flow motif analysis to a player level. We ing the different passing frequencies as a “digital fin- start by breaking down all possible 3-passes motifs gerprint” of a player’s style. The resulting numbers into all the different variations resulting from labelling provide an adequate feature set which can be used a distinguished node in the motif, resulting on a to- in order to construct a measure of similarity between tal of 15 different 3-passes motifs at the player level players. Armed with such a similarity tool, one can (stemming from the 5 motifs for teams). -

A Red Point of View – Issue 1
A RED Point of View GRAEME SHINNIE NEW CAPTAIN NEW SEASON... ISSUE 01 JULY 2017 Welcome... cONTRIBUTORS: It is with great pleasure that I welcome Ryan Crombie: you to “A Red Point of View” the unof- @ryan_crombie ficial online Dons magazine. We are an entirely new publication, dedicated to Ally Begg: bringing you content based upon the @ally_begg club we love. As a regular blogger and writer, I have written many pieces on the Scott Baxter: club I have supported from birth, this perhaps less through choice but family @scottscb tradition. I thank my dad for this. As a re- Matthew Findlay: sult of engaging and sharing my personal @matt_findlay19 writing across social media for several years now, I have grown to discover the monumental online Dons support that Tom Mackinnon: exists across all platforms. The aim of @tom_mackinnon this magazine is to provide a focal point for Aberdeen fans online, to access some Martin Stone: of the best writing that the support have @stonefish100 to offer, whilst giving the writers a plat- form to voice anything and everything Finlay Hall: Dons related. In this first issue we have @FinHall a plethora of content ranging from the pre-season thoughts from one of the Red Army’s finest, Ally Begg, to an ex- Mark Gordon: @Mark_SGordon clusive interview with Darren Mackie, who opens up about his lengthy time at Pittodrie. Guest writer Scott Baxter, Lewis Michie: the club photographer at Aberdeen tells @lewismichie0 what it’s like to photograph the Dons. Finlay Hall analyses the necessity of Ewan Beattie: fanzines and we get some views from @Ewan_Beattie the terraces as fans send in their pieces. -

Sample Download
David Stuart & RobertScotland: Club, Marshall Country & Collectables Club, Country & Collectables 1 Scotland Club, Country & Collectables David Stuart & Robert Marshall Pitch Publishing Ltd A2 Yeoman Gate Yeoman Way Durrington BN13 3QZ Email: [email protected] Web: www.pitchpublishing.co.uk First published by Pitch Publishing 2019 Text © 2019 Robert Marshall and David Stuart Robert Marshall and David Stuart have asserted their rights in accordance with the Copyright, Designs and Patents Act 1988 to be identified as the authors of this work. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior permission in writing of the publisher and the copyright owners, or as expressly permitted by law, or under terms agreed with the appropriate reprographics rights organization. Enquiries concerning reproduction outside the terms stated here should be sent to the publishers at the UK address printed on this page. The publisher makes no representation, express or implied, with regard to the accuracy of the information contained in this book and cannot accept any legal responsibility for any errors or omissions that may be made. A CIP catalogue record for this book is available from the British Library. 13-digit ISBN: 9781785315419 Design and typesetting by Olner Pro Sport Media. Printed in India by Replika Press Scotland: Club, Country & Collectables INTRODUCTION Just when you thought it was safe again to and Don Hutchison, the match go back inside a quality bookshop, along badges (stinking or otherwise), comes another offbeat soccer hardback (or the Caribbean postage stamps football annual for grown-ups) from David ‘deifying’ Scotland World Cup Stuart and Robert Marshall, Scottish football squads and the replica strips which writing’s answer to Ernest Hemingway and just defy belief! There’s no limit Mary Shelley. -

Full Time Report ARSENAL FC VILLARREAL CF
Full Time Report Quarter-Final 2nd leg - Wednesday 15 April 2009 Arsenal Stadium - London ARSENAL FC 11st leg 1 VILLARREAL CF ARSENAL FC win 4-1 on aggregate 320:45 0 (1) (0) half time 14 Theo Walcott 10' half time 21 Łukasz Fabiański 13 Diego López 4 Cesc Fàbregas 2 Gonzalo Rodríguez 5 Kolo Touré 4 Diego Godín 8 Samir Nasri 5 Joan Capdevila 11 Robin van Persie 6 Sebastián Eguren 14 Theo Walcott 18 Mikaël Silvestre 30' 7 Robert Pirès 17 Alexandre Song 10 Cani 18 Mikaël Silvestre 14 Mati Fernández 25 Emmanuel Adebayor 18 Ángel López 27 Emmanuel Eboué 21 Bruno 40 Kieran Gibbs 22 Giuseppe Rossi 24 Vito Mannone 1 Sebastián Viera 2 Abou Diaby 44' 6 Sebastián Eguren 11 Ariel Ibagaza 9 Eduardo 15 NihatKahveci 12 Carlos Vela 45' 16 Joseba Llorente 15 Denilson 1'26" 17 Javi Venta 16 Aaron Ramsey 20 Fabricio Fuentes 26 Nicklas Bendtner 27 Jordi Coach: Coach: Arsène Wenger Manuel Pellegrini Full 51' 10 Cani Full Half Half Total shot(s) 9 16 Total shot(s) 5 9 Shot(s) on target 5 7 59' 4 Diego Godín Shot(s) on target 2 3 Free kick(s) to goal 1 1 in 15 Nihat Kahveci Free kick(s) to goal 1 2 25 Emmanuel Adebayor 60' 64' out 21 Bruno Save(s) 2 3 in 11 Ariel Ibagaza Save(s) 4 4 Corner(s) 1 3 64' out 14 Mati Fernández Corner(s) 2 3 Foul(s) committed 4 15 Foul(s) committed 5 8 Foul(s) suffered 5 8 Foul(s) suffered 4 14 11 Robin van Persie 69' 67' 6 Sebastián Eguren Offside(s) 4 6 Offside(s) 1 2 in 27 Jordi Possession 52% 52% 70' out 10 Cani Possession 48% 48% Ball in play 16'46" 31'29" 15 Denilson in Ball in play 15'41" 29'56" out 77' Total ball in play 32'27" 61'25" 14 Theo Walcott Total ball in play 32'27" 61'25" 2 Abou Diaby in 11 Robin van Persie out 77' in Referee: 26 Nicklas Bendtner out 83' Wolfgang Stark (GER) 25 Emmanuel Adebayor Assistant referees: Jan-Hendrik Salver (GER) Mike Pickel (GER) Fourth official: Babak Rafati (GER) 90' UEFA delegate: Pierino L.G. -

P20 Layout 1
Aussies win Bolt retains final 16Ashes Test 100m18 world title MONDAY, AUGUST 24, 2015 Thereau stuns Juve with late winner Page 19 LIVERPOOL: Manchester City’s Spanish midfielder David Silva (right) shoots past Everton’s English midfielder Gareth Barry (left) and Everton’s Irish defender Seamus Coleman during the English Premier League football match. — AFP Kolarov, Nasri send City top maker Kevin De Bruyne. Manuel Pellegrini’s side have made hour. Silva outfoxed the Everton defence, but Raheem move to Merseyside, almost rued that miss within two min- the perfect start to their quest after recording nine succes- Sterling was not quick enough to react to a low cross when utes of the restart as again City were quickly into their Everton 0 sive league wins for the first time since 1912 and ending a goal might have silenced the Everton supporters who stride. This time Sterling provided the opportunity with a Everton’s unbeaten start in the process. booed every early touch from the former Liverpool winger. clever pass for Silva, who crashed a left-foot shot against a City were unable to include new £32 million ($50.2 mil- Having survived that test, Everton-knowing that a win post. It seemed only a matter of time before a goal, lion, 44.5 million euros) signing Nicolas Otamendi in their would take them to the top of the early league standings- though, and with an hour gone it finally arrived as City squad, with the former Valencia defender still to receive a grew into the game. pounced on the counter-attack. -

Full Time Report AALBORG BK CELTIC FC
Full Time Report Matchday 5 - Tuesday 25 November 2008 Group E - Aalborg Stadion - Aalborg AALBORG BK CELTIC FC 220:45 1 (0) (0) half time half time 1 Karim Zaza 1 Artur Boruc 2 Michael Jakobsen 2 Andreas Hinkel 3 Martin Pedersen 4 Stephen McManus 6 Steve Olfers 5 Gary Caldwell 8 Andreas Johansson 7 Scott McDonald 9 Thomas Augustinussen 8 Scott Brown 14 Jeppe Curth 9 Georgios Samaras 16 Kasper Bøgelund 12 Mark Wilson 18 Caca 19 Barry Robson 21 Kasper Risgård 22 Glenn Loovens 23 Thomas Enevoldsen 25 Shunsuke Nakamura 30 Kenneth Stenild 21 Mark Brown 7 Anders Due 3 Lee Naylor 10 Marek Saganowski 11 Paul Hartley 15 Siyabonga Nomvethe 45' 13 Shaun Maloney 20 Simon Bræmer 1'03" 26 Cillian Sheridan 24 Jens-Kristian Sørensen 48 Darren O'Dea 27 Patrick Kristensen 52 Paul Caddis Coach: Coach: Allan Kuhn Gordon Strachan Full 53' 19 Barry Robson Full Half Half Total shot(s) 4 9 Total shot(s) 2 13 Shot(s) on target 2 4 Shot(s) on target 0 4 Free kick(s) to goal 1 2 Free kick(s) to goal 1 1 Save(s) 0 3 Save(s) 2 3 Corner(s) 4 7 Corner(s) 1 4 Foul(s) committed 7 13 8 Andreas Johansson 69' Foul(s) committed 8 14 Foul(s) suffered 8 14 7 Anders Due in in 26 Cillian Sheridan Foul(s) suffered 7 13 70' 69' Offside(s) 1 3 23 Thomas Enevoldsen out out 9 Georgios Samaras Offside(s) 3 3 10 Marek Saganowski in Possession 48% 47% 14 Jeppe Curth out 70' Possession 52% 53% Ball in play 14'09" 27'12" 18 Caca 73' Ball in play 15'15" 30'37" Total ball in play 29'24" 57'49" Total ball in play 29'24" 57'49" in Referee: 27 Patrick Kristensen out 81' Konrad Plautz (AUT) 3 Martin Pedersen Assistant referees: Armin Eder (AUT) Raimund Buch (AUT) 5 Gary Caldwell 87' in 13 Shaun Maloney 90' out 12 Mark Wilson Fourth official: Stefan Messner (AUT) 90' UEFA delegate: Maurizio Laudi (ITA) 3'17" Attendance: 10,096 22:38:07 CET Goal Booked Sent off Substitution Penalty Owngoal Captain Goalkeeper Misses next match if booked 25 Nov 2008 UEFA Media Information. -

A Comparative Study of After-Match Reports on 'Lost'and 'Won'football
International Journal of Applied Linguistics & English Literature ISSN 2200-3592 (Print), ISSN 2200-3452 (Online) Vol. 4 No. 1; January 2015 Copyright © Australian International Academic Centre, Australia A Comparative Study Of After-match Reports On ‘Lost’ And ‘Won’ Football Games Within The Framework Of Critical Discourse Analysis Biook Behnam Department of English, Islamic Azad University, Tabriz, Iran E-mail: [email protected] Hasan Jahanban Isfahlan (Corresponding Author) Department of English, Islamic Azad University, Tabriz, Iran E-mail: [email protected] Received: 09-07-2014 Accepted: 02-09-2014 Published: 01-01-2015 doi:10.7575/aiac.ijalel.v.4n.1p.115 URL: http://dx.doi.org/10.7575/aiac.ijalel.v.4n.1p.115 Abstract In spite of the obvious differences in research styles, all critical discourse analysts aim at exploring the role of discourse in the production and reproduction of power relations within social structures. Nowadays, after-match written reports are prepared immediately after every football match and provide the readers with the apparently objective representations of important events and occurrences of the game. The authors of this paper analyzed four after-match reports (retrieved from Manchester United’s own website), two regarding their lost games and two on their won games. Hodge and Kress’s (1996) framework was followed in the analysis of the grammatical features of the texts at hand. Also, taking into consideration the pivotal role of lexicalization as one dimension of the textualization process (Fairclough, 2012), vocabulary and more specifically the choice of specific verbs, nouns, adverbs and noun or noun phrase modification were examined. -

Date: 3 March 2012 Opposition: Arsenal Competition
Date: 3 March 2012 Times Echo Telegraph Observer Sunday Telegraph March2012 3 Opposition: Arsenal Standard Independent Guardian Sunday Times Mirror Sun Independent Sunday Mail Sunday Mirror Competition: League Van Persie working on a different plane Wenger hopes Van Persie can make impossible possible against Milan Liverpool 1 Liverpool (1) 1 Koscielny 23 (og) Koscielny 23og Arsenal 2 Arsenal (1) 2 Van Persie 31, 90+2 Van Persie 31 90 Referee: M Halsey Attendance: 44,922 Referee Mark Halsey Amid the avalanche of statistics that rained down on Robin van Persie after goals Attendance 44,922 number 30 and 31 of a stellar season had enhanced Arsenal's prospects of Not content with producing one Kodak moment to win the game, Robin van Champions League football and damaged Liverpool's, there was one, more than Persie re-emerged from the players' tunnel almost an hour later to take any other, that told of a striker at the peak of his powers. photographs of an empty and eerily silent Anfield. Arsenal can only pray their It revealed that in the last four matches that the forward has scored, no brilliant Dutchman wanted to record the day of his first goals goalkeeper has saved one of his shots on target, with seven shots yielding seven against Liverpool and not historic English stadiums he may soon leave behind. goals. It reflected Van Persie's stature in a season of 31 goals that he should have a Maximum efficiency is being achieved. Just as gymnasts once aimed for a perfect major influence on the Champions League aspirations of two clubs on Saturday - ten and fencers look to avoid quite literally being foiled, so goalscorers dream of pushing Arsenal closer to a 15th consecutive campaign among the European elite becoming so unerringly accurate in their finishing that goalkeepers are taken out and Liverpool away from their main target for a third year. -
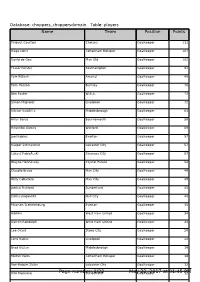
Page Number: 1/22 May 22, 2017 at 01:45 PM
Database: choppers_choppersdomain, Table: players Name Name Team Team PositionPosition PointsPoints Thibaut Courtois Chelsea Goalkeeper 111 Hugo Lloris Tottenham Hotspur Goalkeeper 107 David de Gea Man Utd Goalkeeper 102 Fraser Forster Southampton Goalkeeper 91 Petr ÄŒech Arsenal Goalkeeper 88 Tom Heaton Burnley Goalkeeper 76 Ben Foster W.B.A. Goalkeeper 73 Simon Mignolet Liverpool Goalkeeper 72 VÃctor Valdés Middlesbrough Goalkeeper 63 Artur Boruc Bournemouth Goalkeeper 58 Heurelho Gomes Watford Goalkeeper 58 Joel Robles Everton Goalkeeper 57 Kasper Schmeichel Leicester City Goalkeeper 57 Lukasz FabiaÅ„ski Swansea City Goalkeeper 57 Wayne Hennessey Crystal Palace Goalkeeper 54 Claudio Bravo Man City Goalkeeper 49 Willy Caballero Man City Goalkeeper 49 Jordan Pickford Sunderland Goalkeeper 45 Eldin Jakupović Hull City Goalkeeper 40 Maarten Stekelenburg Everton Goalkeeper 35 Adrián West Ham United Goalkeeper 34 Darren Randolph West Ham United Goalkeeper 34 Lee Grant Stoke City Goalkeeper 28 Loris Karius Liverpool Goalkeeper 24 Brad Guzan Middlesbrough Goalkeeper 19 Michel Vorm Tottenham Hotspur Goalkeeper 16 Ron-Robert Zieler Leicester City Goalkeeper 12 Vito Mannone Page number:Sunderland 1/22 MayGoalkeeper 22, 2017 at 01:45 PM12 Database: choppers_choppersdomain, Table: players Name Name Team Team PositionPosition PointsPoints Jack Butland Stoke City Goalkeeper 11 Sergio Romero Man Utd Goalkeeper 10 Steve Mandanda Crystal Palace Goalkeeper 10 Adam Federici Bournemouth Goalkeeper 4 David Marshall Hull City Goalkeeper 3 Paul Robinson Burnley Goalkeeper 2 Kristoffer Nordfeldt Swansea City Goalkeeper 2 David Ospina Arsenal Goalkeeper 1 Asmir Begovic Chelsea Goalkeeper 1 Wojciech SzczÄ™sny Arsenal Goalkeeper 0 Alex McCarthy Southampton Goalkeeper 0 Allan McGregor Hull City Goalkeeper 0 Danny Ward Liverpool Goalkeeper 0 Joe Hart Man City Goalkeeper 0 Dimitrios Konstantopoulos Middlesbrough Goalkeeper 0 Paulo Gazzaniga Southampton Goalkeeper 0 Jakob Haugaard Stoke City Goalkeeper 0 Boaz Myhill W.B.A. -

West Brom Dig Deep to Win at Everton
SUNDAY, FEBRUARY 14, 2016 SPORTS Long sends soaring Southampton up to sixth They visit Tottenham Hotspur and Arsenal in their next two games. Unbeaten Swansea 0 in their previous four matches, Swansea fielded an unchanged side, with South Korea midfielder Ki Sung-Yueng returning to the bench after missing the 1-1 draw at Southampton 1 home to Crystal Palace with concussion. Southampton recalled four players, among them fit-again pair Matt Targett and Steven Davis, and procured an early sight SWANSEA: Shane Long struck as in-form of goal when Graziano Pelle shot straight at Southampton climbed to within one point Lukasz Fabianski from the edge of the box. of the Premier League’s European places Swansea replied with a tame Andre with a 1-0 victory at relegation-threatened Ayew effort, but the first half did not come Swansea City yesterday. to life until the verge of half-time, when the The Irishman nodded home a cross from teams exchanged good chances in the James Ward-Prowse in the 69th minute at space of a minute. First, Gylfi Sigurdsson the Liberty Stadium as Southampton volleyed over for Swansea from Alberto stretched their unbeaten run to six league Paloschi’s flick-on, before the unmarked games, during which time they have not Long headed straight at Fabianski at the conceded a single goal. other end. Pelle thought he had given It lifted Ronald Koeman’s side up to sixth Southampton the lead just before the hour place in the table, one point below fifth- when he turned the ball in after Fabianski place Manchester United and seven points had dropped it under pressure from Jose off the Champions League berths. -

KT 8-5-2013 Layout 1
SUBSCRIPTION WEDNESDAY, MAY 8, 2013 JAMADA ALTHANI 28, 1434 AH www.kuwaittimes.net 20 dead Man City in Mexico edge gas tanker West Brom truck blast7 20 Dow receives $2.2bn in Max 36º Min 20º damages from Kuwait High Tide 10:48 & 23:57 Low Tide Amount does not include $300m interest for payment delay 04:52 & 17:38 40 PAGES NO: 15802 150 FILS KUWAIT: Kuwait’s state-owned Petrochemical conspiracy theories Industries Co (PIC) said yesterday it reached a final set- tlement with US giant Dow Chemical and paid around $2.2 billion as a penalty for scrapping a joint venture. PIC said in a statement cited by the official KUNA news As usual, agency that the amount did not include $300 million of interest for delaying the payment awarded a year ago. “The settlement stipulates that PIC pays the value of halfway damages and costs as per the ruling of the International Chamber of Commerce (ICC) without the interest of $300 million,” the statement said. solutions The US company said on its website that it has received the cash payment, which “reflects the full dam- ages awarded by the ICC, as well as recovery of Dow’s costs”. PIC confirmed it had made the payment and that it had “exhausted all possible challenges to the award”. Last May, the ICC acting as an international arbitration granted Dow Chemical around $2.2 billion in compen- By Badrya Darwish sation for Kuwait pulling out of the $17.4 billion ven- ture. “Dow and Kuwait share a long history, and payment of this award brings final and appropriate resolution and closure to the issue,” Andrew Liveris, Dow chairman CLEVELAND, Ohio: Amanda Berry (center) is reunited with her sister [email protected] and chief executive officer said in a statement. -

Arsenal's Performance Reminds Me of the Infamous Comical
Saturday Vision, September 3, 2011 English Premiership football 4 Comment Aldrine Nsubuga WENGER OWES IT TO Manchester United’s Anderson (left) challenges Gunner Andrey Arshavin Carrick, the Rafael twin brothers over his head. There was no hiding from his starting line up, knowing place. There was no way he could that Nemanja Vidic, AntonioVa- change the story afterwards. This If Wenger lencia and Darren Fletcher were was the night when he would stop already ruled out by injury. Equal making a fool of himself and admit had taken FERGUSON terms. that his best is not good enough. If Arsenal were going to have score line as football ethos and personality of Robin van Persie, Andrey Ar- The seven-year lie this route deafening as 8-2 the man in charge. shavin, Tomas Rosicky and Theo He had sold a lie to the world in the Premier If Wenger had taken this route Walcott, then United would avail for seven years that Arsenal have two seasons Peague is enough two seasons ago, maybe Fabregas Wayne Rooney, Patrice Evra, Luis the best youth project in England. to last a Big Four and Nasri would still be around. Nani and Ashley Young. Johan But Chris Smalling, Tom Cleverly, ago, maybe club like Arsenal, Maybe, they would have won some Djourou, Laurent Koscielny and Danny Welbeck, Phil Jones, Evans who were at the tail silverware. Maybe, Wenger would Aaron Ramsey, those Gunners with and David de Gea made a mock- Fabregas and Aend of it, in the news for the entire still have his place among the elite relative experience would mix it up ery of Wenger’s preachmony.