Spatio-Temporal Areal Unit Modelling in R with Conditional Autoregressive Priors
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Application of Bagit-Serialized Research Object Bundles for Packaging and Re-Execution of Computational Analyses
Application of BagIt-Serialized Research Object Bundles for Packaging and Re-execution of Computational Analyses Kyle Chard Bertram Ludascher¨ Thomas Thelen Computation Institute School of Information Sciences NCEAS University of Chicago University of Illinois at Urbana-Champaign University of California at Santa Barbara Chicago, IL Champaign, IL Santa Barbara, CA [email protected] [email protected] [email protected] Niall Gaffney Jarek Nabrzyski Matthew J. Turk Texas Advanced Computing Center Center for Research Computing School of Information Sciences University of Texas at Austin University of Notre Dame University of Illinois at Urbana-Champaign Austin, TX South Bend, IN Champaign, IL [email protected] [email protected] [email protected] Matthew B. Jones Victoria Stodden Craig Willisy NCEAS School of Information Sciences NCSA University of California at Santa Barbara University of Illinois at Urbana-Champaign University of Illinois at Urbana-Champaign Santa Barbara, CA Champaign, IL Champaign, IL [email protected] [email protected] [email protected] Kacper Kowalik Ian Taylor yCorresponding author NCSA Center for Research Computing University of Illinois at Urbana-Champaign University of Notre Dame Champaign, IL South Bend, IN [email protected] [email protected] Abstract—In this paper we describe our experience adopting and can be used for verification of computational reproducibil- the Research Object Bundle (RO-Bundle) format with BagIt ity, for example as part of the peer-review process. serialization (BagIt-RO) for the design and implementation of Since its inception, the Whole Tale platform has been “tales” in the Whole Tale platform. A tale is an executable research object intended for the dissemination of computational designed to bring together existing open science infrastructure. -

Real Time Operating Systems Rootfs Creation: Summing Up
Real Time Operating Systems RootFS Creation: Summing Up Luca Abeni Real Time Operating Systems – p. System Boot System boot → the CPU starts executing from a well-known address ROM address: BIOS → read the first sector on the boot device, and executes it Bootloader (GRUB, LILO, U-Boot, . .) In general, load a kernel and an “intial ram disk” The initial fs image isn’t always needed (example: netboot) Kernel: from arm-test-*.tar.gz Initial filesystem? Loaded in RAM without the kernel help Generally contains the boot scripts and binaries Real Time Operating Systems – p. Initial Filesystem Old (2.4) kernels: Init Ram Disk (initrd); New (2.6) kernels: Init Ram Filesystem (initramfs) Generally used for modularized disk and FS drivers Example: if IDE drivers and Ext2 FS are modules (not inside the kernel), how can the kernel load them from disk? Solution: boot drivers can be on initrd / initramfs The bootloader loads it from disk with the kernel The kernel creates a “fake” fs based on it Modules are loaded from it Embedded systems can use initial FS for all the binaries Qemu does not need a bootloader to load kernel and initial FS (-kernel and -initrd) Real Time Operating Systems – p. Init Ram Filesystem Used in 2.6 kernels It is only a RAM FS: no real filesystem metadata on a storage medium All the files that must populate the FS are stored in a cpio package (similar to tar or zip file) The bootloader loads the cpio file in ram At boot time, the kernel “uncompresses” it, creating the RAM FS, and populating it with the files contained in the archive The cpio archive can be created by using the cpio -o -H newc command (see man cpio) Full command line: find . -

CA SOLVE:FTS Installation Guide
CA SOLVE:FTS Installation Guide Release 12.1 This Documentation, which includes embedded help systems and electronically distributed materials, (hereinafter referred to as the “Documentation”) is for your informational purposes only and is subject to change or withdrawal by CA at any time. This Documentation may not be copied, transferred, reproduced, disclosed, modified or duplicated, in whole or in part, without the prior written consent of CA. This Documentation is confidential and proprietary information of CA and may not be disclosed by you or used for any purpose other than as may be permitted in (i) a separate agreement between you and CA governing your use of the CA software to which the Documentation relates; or (ii) a separate confidentiality agreement between you and CA. Notwithstanding the foregoing, if you are a licensed user of the software product(s) addressed in the Documentation, you may print or otherwise make available a reasonable number of copies of the Documentation for internal use by you and your employees in connection with that software, provided that all CA copyright notices and legends are affixed to each reproduced copy. The right to print or otherwise make available copies of the Documentation is limited to the period during which the applicable license for such software remains in full force and effect. Should the license terminate for any reason, it is your responsibility to certify in writing to CA that all copies and partial copies of the Documentation have been returned to CA or destroyed. TO THE EXTENT PERMITTED BY APPLICABLE LAW, CA PROVIDES THIS DOCUMENTATION “AS IS” WITHOUT WARRANTY OF ANY KIND, INCLUDING WITHOUT LIMITATION, ANY IMPLIED WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE, OR NONINFRINGEMENT. -

Bagit File Packaging Format (V0.97) Draft-Kunze-Bagit-07.Txt
Network Working Group A. Boyko Internet-Draft Expires: October 4, 2012 J. Kunze California Digital Library J. Littman L. Madden Library of Congress B. Vargas April 2, 2012 The BagIt File Packaging Format (V0.97) draft-kunze-bagit-07.txt Abstract This document specifies BagIt, a hierarchical file packaging format for storage and transfer of arbitrary digital content. A "bag" has just enough structure to enclose descriptive "tags" and a "payload" but does not require knowledge of the payload's internal semantics. This BagIt format should be suitable for disk-based or network-based storage and transfer. Status of this Memo This Internet-Draft is submitted in full conformance with the provisions of BCP 78 and BCP 79. Internet-Drafts are working documents of the Internet Engineering Task Force (IETF). Note that other groups may also distribute working documents as Internet-Drafts. The list of current Internet- Drafts is at http://datatracker.ietf.org/drafts/current/. Internet-Drafts are draft documents valid for a maximum of six months and may be updated, replaced, or obsoleted by other documents at any time. It is inappropriate to use Internet-Drafts as reference material or to cite them other than as "work in progress." This Internet-Draft will expire on October 4, 2012. Copyright Notice Copyright (c) 2012 IETF Trust and the persons identified as the document authors. All rights reserved. This document is subject to BCP 78 and the IETF Trust's Legal Provisions Relating to IETF Documents (http://trustee.ietf.org/license-info) in effect on the date of Boyko, et al. -

How to Extract a Deb Package on Debian, Ubuntu, Mint Linux and Other Non Debian Based Distributions
? Walking in Light with Christ - Faith, Computers, Freedom Free Software GNU Linux, FreeBSD, Unix, Windows, Mac OS - Hacks, Goodies, Tips and Tricks and The True Meaning of life http://www.pc-freak.net/blog How to extract a deb package on Debian, Ubuntu, Mint Linux and other non debian based distributions Author : admin How to extract a deb package? Have you ever had a debian .deb package which contains image files you need, but the dependencies doesn't allow you to install it on your Debian / Ubuntu / Mint Linux release? I had just recently downloaded the ultimate-edition-themes latest release v 0.0.7 a large pack of GNOME Themes and wanted to install it on my Debian Stretch Linux but I faced problems because of dependencies when trying to install with dpkg. That is why I took another appoarch and decided to only extract the necessery themes from the archive only with dpkg. Here is how I have extracted ultimate-edition-themes-.0.0.7_all.deb ; dpkg -x ultimate-edition-themes-.0.0.7_all.deb /tmp/ultimate-edition-themes 1 / 3 ? Walking in Light with Christ - Faith, Computers, Freedom Free Software GNU Linux, FreeBSD, Unix, Windows, Mac OS - Hacks, Goodies, Tips and Tricks and The True Meaning of life http://www.pc-freak.net/blog So how dpkg extracts the .deb file? Debian .deb packages are a regular more in Wikipedia - Unix archive files (ar) . The structure of a deb file consists of another 3 files (2 tar.gzs and one binary) as follows: debian-binary: regular text file, contains the version of the deb package format control.tar.gz: compressed file, contains file md5sums and control directory for the deb package data.tar.gz: compressed file, contains all the files which will be installed Basicly if you're on a Linux distribution that lacks dpkg you can easily extract .deb binary using GNU AR command (used to create, modify extract Unix ar files and is the GNU / Linux equivallent of the UNIX ar command). -
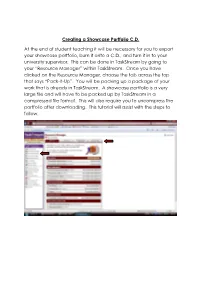
Creating a Showcase Portfolio CD
Creating a Showcase Portfolio C.D. At the end of student teaching it will be necessary for you to export your showcase portfolio, burn it onto a C.D., and turn it in to your university supervisor. This can be done in TaskStream by going to your “Resource Manager” within TaskStream. Once you have clicked on the Resource Manager, choose the tab across the top that says “Pack-It-Up”. You will be packing up a package of your work that is already in TaskStream. A showcase portfolio is a very large file and will have to be packed up by TaskStream in a compressed file format. This will also require you to uncompress the portfolio after downloading. This tutorial will assist with the steps to follow. The next step is to select the work you would like TaskStream to package. This is done by clicking on the tab for selecting work. You will then be asked what type of work you want to package. Your showcase portfolio is a presentation portfolio, so you will click there and click next step. The next step will be to choose the presentation portfolio you want packaged, check the box, and click next step. TaskStream will confirm your selection and then ask you to choose the type of file you need your work to be packaged into. If you are using a computer with a Windows operating system, you will choose a zip file. If you are using a computer with a Macintosh operating system, you will choose a sit file. You will also be asked how you would like TaskStream to notify you that they have completed the task of packing up your work. -

Conda-Build Documentation Release 3.21.5+15.G174ed200.Dirty
conda-build Documentation Release 3.21.5+15.g174ed200.dirty Anaconda, Inc. Sep 27, 2021 CONTENTS 1 Installing and updating conda-build3 2 Concepts 5 3 User guide 17 4 Resources 49 5 Release notes 115 Index 127 i ii conda-build Documentation, Release 3.21.5+15.g174ed200.dirty Conda-build contains commands and tools to use conda to build your own packages. It also provides helpful tools to constrain or pin versions in recipes. Building a conda package requires installing conda-build and creating a conda recipe. You then use the conda build command to build the conda package from the conda recipe. You can build conda packages from a variety of source code projects, most notably Python. For help packing a Python project, see the Setuptools documentation. OPTIONAL: If you are planning to upload your packages to Anaconda Cloud, you will need an Anaconda Cloud account and client. CONTENTS 1 conda-build Documentation, Release 3.21.5+15.g174ed200.dirty 2 CONTENTS CHAPTER ONE INSTALLING AND UPDATING CONDA-BUILD To enable building conda packages: • install conda • install conda-build • update conda and conda-build 1.1 Installing conda-build To install conda-build, in your terminal window or an Anaconda Prompt, run: conda install conda-build 1.2 Updating conda and conda-build Keep your versions of conda and conda-build up to date to take advantage of bug fixes and new features. To update conda and conda-build, in your terminal window or an Anaconda Prompt, run: conda update conda conda update conda-build For release notes, see the conda-build GitHub page. -

Debian Packaging Tutorial
Debian Packaging Tutorial Lucas Nussbaum [email protected] version 0.27 – 2021-01-08 Debian Packaging Tutorial 1 / 89 About this tutorial I Goal: tell you what you really need to know about Debian packaging I Modify existing packages I Create your own packages I Interact with the Debian community I Become a Debian power-user I Covers the most important points, but is not complete I You will need to read more documentation I Most of the content also applies to Debian derivative distributions I That includes Ubuntu Debian Packaging Tutorial 2 / 89 Outline 1 Introduction 2 Creating source packages 3 Building and testing packages 4 Practical session 1: modifying the grep package 5 Advanced packaging topics 6 Maintaining packages in Debian 7 Conclusions 8 Additional practical sessions 9 Answers to practical sessions Debian Packaging Tutorial 3 / 89 Outline 1 Introduction 2 Creating source packages 3 Building and testing packages 4 Practical session 1: modifying the grep package 5 Advanced packaging topics 6 Maintaining packages in Debian 7 Conclusions 8 Additional practical sessions 9 Answers to practical sessions Debian Packaging Tutorial 4 / 89 Debian I GNU/Linux distribution I 1st major distro developed “openly in the spirit of GNU” I Non-commercial, built collaboratively by over 1,000 volunteers I 3 main features: I Quality – culture of technical excellence We release when it’s ready I Freedom – devs and users bound by the Social Contract Promoting the culture of Free Software since 1993 I Independence – no (single) -

Building the Ios Wrapper Version 1.3.0+
Building The iOS Wrapper Version 1.3.0+ Contents Introduction.................................................................................................................................................... 2 Setting Up The Build Environment ................................................................................................................ 2 Install xCode .............................................................................................................................................. 2 Set Up Code Signing Requirements ......................................................................................................... 2 Certificates ............................................................................................................................................. 3 Identifiers ............................................................................................................................................... 4 Devices .................................................................................................................................................. 5 Provisioning Profile ................................................................................................................................ 5 Open The Project ...................................................................................................................................... 6 Configuring The App .................................................................................................................................... -

Forcepoint DLP Supported File Formats and Size Limits
Forcepoint DLP Supported File Formats and Size Limits Supported File Formats and Size Limits | Forcepoint DLP | v8.8.1 This article provides a list of the file formats that can be analyzed by Forcepoint DLP, file formats from which content and meta data can be extracted, and the file size limits for network, endpoint, and discovery functions. See: ● Supported File Formats ● File Size Limits © 2021 Forcepoint LLC Supported File Formats Supported File Formats and Size Limits | Forcepoint DLP | v8.8.1 The following tables lists the file formats supported by Forcepoint DLP. File formats are in alphabetical order by format group. ● Archive For mats, page 3 ● Backup Formats, page 7 ● Business Intelligence (BI) and Analysis Formats, page 8 ● Computer-Aided Design Formats, page 9 ● Cryptography Formats, page 12 ● Database Formats, page 14 ● Desktop publishing formats, page 16 ● eBook/Audio book formats, page 17 ● Executable formats, page 18 ● Font formats, page 20 ● Graphics formats - general, page 21 ● Graphics formats - vector graphics, page 26 ● Library formats, page 29 ● Log formats, page 30 ● Mail formats, page 31 ● Multimedia formats, page 32 ● Object formats, page 37 ● Presentation formats, page 38 ● Project management formats, page 40 ● Spreadsheet formats, page 41 ● Text and markup formats, page 43 ● Word processing formats, page 45 ● Miscellaneous formats, page 53 Supported file formats are added and updated frequently. Key to support tables Symbol Description Y The format is supported N The format is not supported P Partial metadata -

Big Data and Supercomputing Using R
Big Data and R R Packages for Big Data A Case Study Super Computing Using R Big Data and Supercomputing Using R Jie Yang Department of Mathematics, Statistics, and Computer Science University of Illinois at Chicago October 15, 2015 Big Data and R R Packages for Big Data A Case Study Super Computing Using R 1 Big Data and R What is big data Why using R 2 R Packages for Big Data Sources for R and its packages R packages for big data management R packages for numerical calculation involving big data Speeding up Scaling up 3 A Case Study Airline on-time performance data Analyzing big data 4 Super Computing Using R Argo Cluster at UIC Install R at Argo Run R batch job at Argo Big Data and R R Packages for Big Data A Case Study Super Computing Using R What is Big Data Big data is a broad term for data sets so large or complex that traditional data processing applications are inadequate (Wikipedia). Data is large if it exceeds 20% of the random access memory (RAM) on a given machine, and massive if it exceeds 50% (Emerson and Kane, 2012). Big Data represents the Information assets characterized by such a High Volume (amount of data), Velocity (speed of data in and out) and Variety (range of data types and sources) to require specific Technology and Analytical Methods for its transformation into value (De Mauro et al., 2015, also known as Gartner's definition of the 3Vs). Big Data and R R Packages for Big Data A Case Study Super Computing Using R Why Using R Handling big data requires high performance computing, which is undergoing rapid change. -

Downloading the Dissociation Curves Software
Downloading the Dissociation Curves Software Introduction This page provides instructions for downloading the Dissociation Curves 1.0 software package to a Macintosh computer connected to the Internet, using either Netscape or Internet Explorer. You can also download the software package to a Windows PC using Internet Explorer, then transfer it to a Macintosh, e.g., with a PC-formatted Zip disk. To print a copy of these instructions, use your browser's Print command. To return to the download page, use your browser's Back command. Compatibility The Dissociation Curves 1.0 software package is compatible with SDS 1.7 or later. The latest version of SDS software for the ABI PRISMÒ 7700 Sequence Detection System can be downloaded from the Applied Biosystems web site at www.appliedbiosystems.com/support/software/7700/updates.cfm A description of the appropriate thermal protocol to use for acquisition of dissociation curve data (i.e., a programmed ramp) is available in the SDS 1.7 user bulletin. How the Software is Packaged The Dissociation Curves 1.0 software package is contained in a folder called "Dissociation Curves 1.0 f", which contains the software program, Help Files, and Sample Files. In order to reduce the size of the download, the entire folder contents were compressed into a single Stuffit file with a ".sit" extension. For distribution on the web, the ".sit" Stuffit file was then encoded to a BinHex format file with a ".hqx" extension. This format minimizes problems with various web servers and browsers that are commonly used on the Internet. Downloading the software package is thus a three step process: 1.