DOCSLIB.ORG

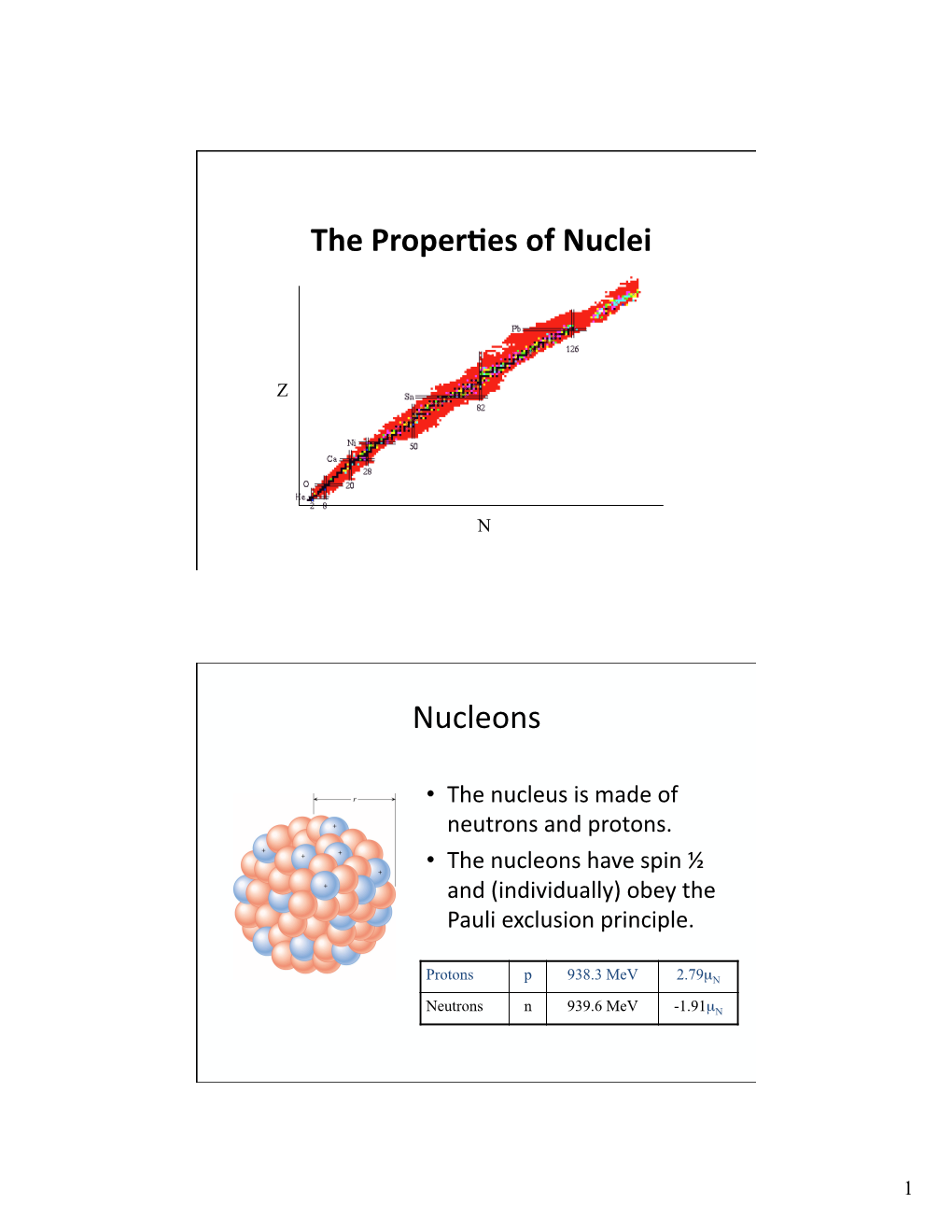
The Proper Es of Nuclei Nucleons

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Proper Es of Nuclei Nucleons The Properes of Nuclei Z N Nucleons • The nucleus is made of neutrons and protons. • The nucleons have spin ½ and (individually) obey the Pauli exclusion principle. Protons p 938.3 MeV 2.79µN Neutrons n 939.6 MeV -1.91µN 1 Nuclides • A nuclide is a nucleus with a specific number of neutrons and a specific number of protons. • Z = # of protons N = # of neutrons • A = mass number (N+Z) X = chemical symbol • Isotopes = same Z, different N • Isotones = same N, different Z Example: Carbon-14 or Nuclear ProperHes Forces, Masses and Shapes 2 Nuclear Forces • The Strong Nucleon-Nucleon Force – Binds nucleons together – Short range (≈ 3 fm) – APracHve over most distances – Repulsive “hard” core – Spin dependent – Charge Independent (n-n, n-p, and p-p forces the same aer electrostac repulsion removed) – The potenHal “well” that two nucleons experience is about 40 MeV deep and a few fermi wide. n-p and p-p interacHons 3 Nuclear PotenHal • Each proton or neutron in the nucleus feels an average force from the other nucleons. • This force can be modeled as a potenHal well. SiZe and Shape • Describing the nucleus : – Charge density – Mass density – Force density • Most (but not all) spherical 1/3 -15 R = r0A r0 = 1.2 x 10 m =1.2 fm 4 SiZe and Shape The surface thickness, t, is roughly constant across nuclei at approximately 2.3 fm. SiZe and Shape • Isomers (shape) • Most nuclei are spherical. • Some deformed nuclei in Z= 57 – 71 region 5 Determining the siZe of the nucleus • The siZe of nuclei can be determined in a variety of ways – Electron Scaering – Mirror Nuclei Decays – Alpha Scaering – APenuaon of neutron beams Determining the siZe of the nucleus: Electron Scaering • Stanford Linear Accelerator 500 MeV electrons, λ = 2.5 fm Electrons scatter from nuclear charge density 6 Determining the siZe of the nucleus: Electron Scaering • DiffracHon paerns from high energy electrons scaered from 16O and 12C. • The minimum occurs at sinθ = 0.61 λ/R • R = (1.23 ±0.01)A1/3 fm Determining the siZe of the nucleus: Electron Scaering • Radius from electron scaering experiments. • R = (1.23 ±0.01)A1/3 fm 7 Determining the siZe of the nucleus: Mirror Nuclei • Mirror nuclei are isobars with the proton and neutron numbers reversed. • As the strong force is independent of charge the mirror nuclear should differ only in terms of electrostac energy. Determining the siZe of the nucleus: Mirror Nuclei • 15N and 15O are mirror nuclei. • The decay energy should be • The 15O nucleus can equal to the electrostac spontaneously emit a positron energy difference. and neutrino decaying to 15N. • Analysis gives R = 1.2 A1/3 fm 8 Determining the siZe of the nucleus: Alpha Scaering Alpha particles are close enough to feel the strong nuclear force. • To probe maer distribuHon strongly interacHng parHcles are used. Determining the siZe of the nucleus: Neutron APenuaon • A beam of fast neutrons is aenuated by interacHng via the strong force with the nuclei (i.e. neutrons are absorbed or scaered). • R = 1.4 A1/3 fm 9 Mass of Nuclei • Mass Spectrometers can separate isotopes by their mass. Mass and Binding Energy • When two or more objects come together under the influence of an aracHve force, they become bound and the system loses mass. This lost mass leaves the system as energy: E = mc2 10 Binding energies • The nuclear binding energy is the difference between isolated neutrons and protons and the bound nucleus. • It is tradiHonal to use atomic masses in the binding energy formula. Binding Energies - Example 11 Curve of the Binding Energy Binding Energies and the Liquid Drop Model • The liquid drop model provides a theoreHcal framework to develop a general formula for binding energies: • Energies associated with – Volume – Surface area – Coulomb repulsion between protons 12 Semi-Empirical Binding Energy Volume Electrostatic Pairing Surface Area Symmetry Paring: Symmetry and Pairing • The Pauli principle requires we fill up the energy levels with one proton or neutron per state. • Fill up levels with n and p individually • Spin pairing • Proton potenHal is slightly higher in energy 13 Chart of the Nuclides • Stable Nuclei: – Light Nuclei: N ~ Z – Heavy Nuclei: N > Z Pairing InteracHon • Stable Nuclei: – 266 stable nuclides – 159 – even Z, even N – 50 – odd Z, even N – 53 – even Z, odd N – 4 – odd Z, odd N 14 Neutron and Proton Separaon Energies • Energy needed to remove one neutron from a nucleus • Energy needed to remove one proton from a nucleus Properes of Nuclei MagneHc and Electric 15 MagneHc moment of electron Nuclear MagneHc Moments • Proton: g = 5.5856912 +/- 0.0000022 • Neutron: g = -3.8260837 +/- 0.0000018 • Nuclei have magneHc moments that are combinaons of intrinsic nucleon moments and “orbital magnet moments” 16 Electric Quadrupole Moments • The charge distribuHon of the nucleus can be represented as a sum in terms of mulHpole moments. Hyperfine Spling • The magneHc and electric properHes of nuclei can be detected through the coupling of the EM fields of the nuclei with atomic electrons. • MagneHc hyperfine spling arises from the dipole-dipole interacHon between the nucleus and the atom. 21cm line of Hydrogen 17 Models of Nuclei Models of Nuclei • Independent ParHcle Models – “Shell Models” – Based on an analogy to harmonic oscillators and square wells. – Assume nucleus has some stac average potenHal made from the individual N-N interacHons (mean field approximaon.) • CollecHve Models – Based on analogies to fluid dynamics – Nucleus made of a “nuclear maer” – Allows non-spherical shapes and collecHve moHons 18 The Shell Model • Model the nucleus by a potenHal well of some shape. • Protons and neutrons fill the well according to the Pauli Principle. • Harmonic oscillator? • Square well? The Shell Model • The large gaps between levels we associate with closed shells. • Notaon: nl • n counts the number of levels with a given angular momentum l 19 Wood-Saxon PotenHal • An intermediate form based on nuclear maer distribuHon. Shell Structure with Wood-Saxon Spling differs somewhat at higher levels. 20 Do Nuclei have shell structure? • Binding energy of last neutron Do Nuclei have shell structure? • Neutron absorpHon cross-secHons 21 Do Nuclei have shell structure? • Binding energy vs. formula Do Nuclei have shell structure? • Quadrupole Moments 22 Magic Numbers • There are numbers of neutrons and protons that yield parHcularly Hghtly bound nuclei. • The magic numbers: 2, 8, 20, 28, 50, 82, 126 • 15N – magic neutron number • 58Ni – magic proton number • 40Ca – doubly magic Magic Numbers • 2, 8, 20, 28, 50, 82, 126 23 Spin Orbit InteracHon Goeppert-Mayer and Jensen Nobel Prize1963 Spin-Orbit InteracHon • The total angular momentum of a nucleon is labeled by j. • As a single nucleon has s= ½ the possible j values are 24 Spin Orbit InteracHon • The expectaon value is • And the jth level has a degeneracy of Spin Orbit InteracHon • Consider the 1f level which has a degeneracy of 14. • Possible j values are 5/2 and 7/2 thus the levels are 1f5/2 and 1f7/2 . • The degeneracy of these levels (2j+1) are 6 and 8 respecHvely. • The spin-orbit potenHal causes an energy difference proporHonal to the difference in the expectaon value of l⋅s for each state. • The energy spling increases with increasing orbital angular momentum l. If fSO(r) is negave then the states with the higher j will be pushed down in energy. 25 Spin-Orbit InteracHon 2, 8, 20, 28, 50, 82, 126, 184 PredicHng ProperHes of Nuclei from the Shell Model • Ground State spin and parity • MagneHc Dipole Moments • Electric Quadrupole Moments • Excited States 26 Ground State Properes • The group state nuclear spin and parity is determined primarily by the valance nucleon. • Closed shells have j = 0 and + parity. • Like nucleons pair up to give j = 0. • The unpaired nucleon(s) outside the closed shell determine spin and parity. • By this model all even-even nuclei should have a ground state spin of 0. • Parity is determined by the orbital angular momentum of the valance nucleons: (-1)l Example: Oxygen and Nitrogen • 16O – Z=8, N=8 (doubly Magic) – ground state is 0+ • 17O – Z=8, N=9 (1 neutron outside closed shell) – ground state is 5/2+ • 15N – Z=7, N=8 (neutron shell closed, one unpaired proton) – ground state is 1/2- 27 MagneHc Moments • In the simplest model the magneHc moment of the nucleus is determined by the valence nucleon(s). • The magneHc moment is a combinaon of the spin magneHc moment and the orbital magneHc moment of the nucleon. • But lZ and sZ do not have well defined value in a system of well-defined jZ. • There are two possible j states: MagneHc Moments • The comparison between the computed (lines) and measured values (dots) is shown. The lines are known as “Schmidt” lines. odd Z odd N 28 Excited States • We should be able to explain the spin and parity of the excited states of nuclei by using the shell model. • As energy is added to the nucleus the nucleons are promoted to higher levels in the shell model. Excited states ?? (8) 1/2 - ?? 3/2 - mirror nuclides Pairing energy increases with Independent particle shell model states 29 All have 1 unpaired nucleon in f5/2 level. Multiple nucleon excited states 2p3/2 1f5/2 1 nucleon beyond 20 CollecHve Models • Nuclei made of strongly interacHng nuclear maer. • Deformed (non-spherical nuclei). • Rotaonal, vibraonal moHons of nuclei. • Liquid-drop Model – Binding Energies 30 Even-Even Nuclei Low Lying Energy Levels of 130Sn Even-Even Nuclei Energies of the lowest 2+ states of even-even nuclei 31 Nuclear Vibraons • Constant density shape deformaons quadrupole sextupole octopole phonons: 1 2 3 2+ 0+,2+,4+ 0+,2+,3+,4+,6++ Nuclear Rotaons • Some nuclei have non-spherical shapes.
Load more

Recommended publications
  • Range of Usefulness of Bethe's Semiempirical Nuclear Mass Formula
    RANGE OF ..USEFULNESS OF BETHE' S SEMIEMPIRIC~L NUCLEAR MASS FORMULA by SEKYU OBH A THESIS submitted to OREGON STATE COLLEGE in partial fulfillment or the requirements tor the degree of MASTER OF SCIENCE June 1956 TTPBOTTDI Redacted for Privacy lrrt rtllrt ?rsfirror of finrrtor Ia Ohrr;r ef lrJer Redacted for Privacy Redacted for Privacy 0hrtrurn of tohoot Om0qat OEt ttm Redacted for Privacy Dru of 0rrdnrtr Sohdbl Drta thrrlr tr prrrEtrl %.ifh , 1,,r, ," r*(,-. ttpo{ by Brtty Drvlr ACKNOWLEDGMENT The author wishes to express his sincere appreciation to Dr. G. L. Trigg for his assistance and encouragement, without which this study would not have been concluded. The author also wishes to thank Dr. E. A. Yunker for making facilities available for these calculations• • TABLE OF CONTENTS Page INTRODUCTION 1 NUCLEAR BINDING ENERGIES AND 5 SEMIEMPIRICAL MASS FORMULA RESEARCH PROCEDURE 11 RESULTS 17 CONCLUSION 21 DATA 29 f BIBLIOGRAPHY 37 RANGE OF USEFULNESS OF BETHE'S SEMIEMPIRICAL NUCLEAR MASS FORMULA INTRODUCTION The complicated experimental results on atomic nuclei haYe been defying definite interpretation of the structure of atomic nuclei for a long tfme. Even though Yarious theoretical methods have been suggested, based upon the particular aspects of experimental results, it has been impossible to find a successful theory which suffices to explain the whole observed properties of atomic nuclei. In 1936, Bohr (J, P• 344) proposed the liquid drop model of atomic nuclei to explain the resonance capture process or nuclear reactions. The experimental evidences which support the liquid drop model are as follows: 1. Substantially constant density of nuclei with radius R - R Al/3 - 0 (1) where A is the mass number of the nucleus and R is the constant of proportionality 0 with the value of (1.5! 0.1) x 10-lJcm~ 2.
    [Show full text]
  • Neutron Deficient Exotic Nuclei and the Physics of the Proton Rich
    Report on the second EURISOL User Group Topical Meeting 1 Neutron deficient exotic nuclei and the Physics of the proton rich side of the nuclear chart. Colegio Mayor Rector Peset, Valencia, Spain, 21-23 February 2011. The research leading to these results has received funding from the European Union Seventh Framework Programme FP7/2007- 2013 under Grant Agreement n. 262010 - ENSAR. The EC is not liable for any use that can be made on the information contained herein. The workshop was partially supported by CPAN and IFIC (CSIC-Univ. of Valencia), Spain. 1Coordinated by Berta Rubio, IFIC, Valencia, Spain and Angela Bonaccorso, INFN, Sez. di Pisa, Italy. 1 EURISOL SECOND TOPICAL MEETING “Neutron-deficient nuclei and the physics of the proton-rich side of the nuclear chart” Foreword This booklet contains the highlights of the second EURISOL Topical Meeting which was held in Valencia from 21st to 23rd February 2011. It followed the EURISOL Topical Meeting in Catania on “The formation and structure of r-process nuclei, between N=50 and 82 (including 78Ni and 132Sn areas)”. It was organised by the EURISOL Users Group and supported by the European Commission (ENSAR project), CPAN (Centro Nacional de Física de Partículas, Astropartículas y Nuclear, Spain) and IFIC (Instituto de Física Corpuscular, Spain). During the two and a half days of the meeting an interesting and dense programme was accommodated. Seventy participants, including almost all members of the previous and present EURISOL User Group Executive Committee contributed either to the presentations or to the lively discussions. The programme and the presentations are available at the workshop web site http://ific.uv.es/~eug-valencia.
    [Show full text]
  • Mirror Nuclei, A<=
    Atomic Energy of Canada Limited MIRROR NUCLEI, A < 100 by J.C. HARDY Presented as an invited talk to the Canadian Association of Physicists meeting held in Montreal, June 18-21, 1973 Chalk River Nuclear Laboratories Chalk River, Ontario August 1973 AECL-4604 Atomic Energy of Canada Limited MIRROR NUCLEI, A <: 100 by J.C. HARDY Presented as an invited talk to the Canadian Association of Physicists meeting held in Montreal, June 18-21, 1973. Chalk River Nuclear Laboratories Chalk River, Ontario August 1973 AECL- Mirror Nuclei, A <, ICC by J.C Hardy ABSTRACT The effects of charge-dependent forces are described, and their dependence on the nuclear mass is discussed, it is proposed that large isospin impurities may occur in heavier nuclei (A <s 10G) with N ~ Z. several classes of p-decay experi- ment are sensitive to these effects, and a detailed description is given of recent chalk River experiments to study the super- allowed decay of 0*, T7 = -1 nuclei. This work has included the first measurement of mirror Fermi decay branches within a T = 1 multiplet. These and other data on superallowed p-decay are analyzed with particular emphasis on the charge dependent corrections to which mirror comparisons are particularly sensitive. The results are discussed in terms of the theory of weak interactions and the question of the existence of a heavy intermediate vector boson. It is suggested that some discrepancies for nuclei with A > 40 may be attributed to the proposed increase in charge dependent mixing. Some other experimental evidence suggesting the same conclusion is also given.
    [Show full text]
  • Relativistic Deformed Mean-Field Calculation of Binding Energy Differences of Mirror Nuclei
    Instituto de Física Teórica IFT Universidade Estadual Paulista IFT-P.003/96 TAUP-2310-95 Relativistic deformed mean-field calculation of binding energy differences of mirror nuclei W. Koepf School of Physics and Astronomy Tel Aviv University 69978 Ramat Aviv Israel G. Krein Instituto de Física Teórica Universidade Estadual Paulista Rua Pamplona 145 01405-900 - São Paulo, S.P. Brazil and L. A. Barreiro Instituto de Física Universidade de São Paulo Caixa Postal 66318 05389-970 - São Paulo, S.P. Brazil ? 7 US 1 Instituto de Física Teórica Universidade Estadual Paulista Rua Pamplona, 145 01405-900 - São Paulo, S.P. Brazil Telephone: 55 (11) 251.5155 Telefax: õõ (11) 288.8224 Telex: 55 (11) 31870 UJMFBR Electronic Address: [email protected] 47857::LIBRARY TAUP-2310-95, IFT-P.003/96,nucI-th/9601027 1. Introduction. Conventional nuclear theory, based on the Schrodingcr equation, 1ms difficulties in explaining the binding energy differences of mirror nuclei [1,2]. The major Relativistic deformed mean-field calculation of binding energy contribution to the energy difference comes from the Coulomb force, and a variety of isospm differences of mirror nuclei breaking effects provide small contributions. The difficulty in reproducing the experimental values is kaown in the literature as the Okamofco-Nolen-Schiffer anomaly (ONSA). Several W. Koepf nuclear structure effects such as correlations, core polarization and isospin mixing have been School of Physics and Astronomy, Tel Aviv University, 69978 Ramat Aviv, Israel invoked to resolve the anomaly without success [3]. Since Okamoto and Pask [4] and Negele [5] suggested that the discrepancy could he G.
    [Show full text]
  • A Broken Nuclear Mirror to Ornithine Being Mobilized in Cytoplasmic Pathways Leading to Spermidine Production
    Spermidine is a type of molecule called a adenosine-receptor expression and function forged in life; what other chains are forged in polyamine. It is mainly produced from a meta- between the species8, and therefore efforts to cell death? bolic pathway that converts the amino acid use these metabolites to treat human disease arginine to polyamines through intermediates might prove challenging. Douglas R. Green is in the Department of that include the molecule ornithine (Fig. 1). Medina and colleagues’ work opens rich Immunology, St. Jude Children’s Research Medina and colleagues traced the conversion possibilities for future investigations into Hospital, Memphis, Tennessee 38105, USA. of arginine to spermidine by this pathway, and how apoptosis triggers metabolic changes, e-mail: [email protected] found that cells induced to undergo apoptosis and how the regulated release of metabolites increased their synthesis of spermidine and its influences tissues. In contrast to apoptosis, 1. Medina, C. B. et al. Nature 580, 130–135 (2020). precursor, the molecule putrescine, before other forms of cell death, such as regulated 2. Green, D. R. Cell Death: Apoptosis and Other Means to an dying. The apoptotic cells released spermi- forms of necrosis, have profoundly different End 2nd edn (Cold Spring Harb. Lab. Press, 2018). 3. Lüthi, A. U. & Martin, S. J. Cell Death Differ. 14, 641–650 dine, but not putrescine. Spermidine release effects on surrounding cells, and whether (2007). occurred in a PANX1-dependent manner. and how changes in metabolism triggered 4. Kerr, J. F. R., Wyllie, A. H. & Currie, A. R. Br. J. Cancer 26, Although this phenomenon was monitored by those cell-death pathways influence their 239–257 (1972).
    [Show full text]
  • Nucleus Nucleus the Massive, Positively Charged Central Part of an Atom, Made up of Protons and Neutrons
    Madan Mohan Malaviya Univ. of Technology, Gorakhpur MPM: 203 NUCLEAR AND PARTICLE PHYSICS UNIT –I: Nuclei And Its Properties Lecture-4 By Prof. B. K. Pandey, Dept. of Physics and Material Science 24-10-2020 Side 1 Madan Mohan Malaviya Univ. of Technology, Gorakhpur Size of the Nucleus Nucleus the massive, positively charged central part of an atom, made up of protons and neutrons • In his experiment Rutheford observed that the light nuclei the distance of closest approach is of the order of 3x10−15 m. • The distance of closest approach, at which scattering begins to take place was identified as the measure of nuclear size. • Nuclear size is defined by nuclear radius, also called rms charge radius. It can be measured by the scattering of electrons by the nucleus. • The problem of defining a radius for the atomic nucleus is similar to the problem of atomic radius, in that neither atoms nor their nuclei have definite boundaries. 24-10-2020 Side 2 Madan Mohan Malaviya Univ. of Technology, Gorakhpur Nuclear Size • However, the nucleus can be modelled as a sphere of positive charge for the interpretation of electron scattering experiments: because there is no definite boundary to the nucleus, the electrons “see” a range of cross-sections, for which a mean can be taken. • The qualification of “rms” (for “root mean square”) arises because it is the nuclear cross-section, proportional to the square of the radius, which is determining for electron scattering. • The first estimate of a nuclear charge radius was made by Hans Geiger and Ernest Marsden in 1909, under the direction of Ernest Rutherford.
    [Show full text]
  • Chapter 12 Charge Independence and Isospin
    Chapter 12 Charge Independence and Isospin If we look at mirror nuclei (two nuclides related by interchanging the number of protons and the number of neutrons) we find that their binding energies are almost the same. In fact, the only term in the Semi-Empirical Mass formula that is not invariant under Z (A-Z) is the Coulomb term (as expected). ↔ Z2 (Z N)2 ( 1) Z + ( 1) N a B(A, Z ) = a A a A2/3 a a − + − − P V − S − C A1/3 − A A 2 A1/2 Inside a nucleus these electromagnetic forces are much smaller than the strong inter-nucleon forces (strong interactions) and so the masses are very nearly equal despite the extra Coulomb energy for nuclei with more protons. Not only are the binding energies similar - and therefore the ground state energies are similar but the excited states are also similar. 7 7 As an example let us look at the mirror nuclei (Fig. 12.2) 3Li and 4Be, where we see that 7 for all the states the energies are very close, with the 4Be states being slightly higher because 7 it has one more proton than 3Li. All this suggests that whereas the electromagnetic interactions clearly distinguish between protons and neutrons the strong interactions, responsible for nuclear binding, are ‘charge independent’. Let us now look at a pair of mirror nuclei whose proton number and neutron number 6 6 differ by two, and also the nuclide between them. The example we take is 2He and 4Be, which are mirror nuclei. Each of these has a closed shell of two protons and a closed shell of 6 6 two neutrons.
    [Show full text]
  • Nuclear Physics and Astrophysics SPA5302, 2019 Chris Clarkson, School of Physics & Astronomy [email protected]
    Nuclear Physics and Astrophysics SPA5302, 2019 Chris Clarkson, School of Physics & Astronomy [email protected] These notes are evolving, so please let me know of any typos, factual errors etc. They will be updated weekly on QM+ (and may include updates to early parts we have already covered). Note that material in purple ‘Digression’ boxes is not examinable. Updated 16:29, on 05/12/2019. Contents 1 Basic Nuclear Properties4 1.1 Length Scales, Units and Dimensions............................7 2 Nuclear Properties and Models8 2.1 Nuclear Radius and Distribution of Nucleons.......................8 2.1.1 Scattering Cross Section............................... 12 2.1.2 Matter Distribution................................. 18 2.2 Nuclear Binding Energy................................... 20 2.3 The Nuclear Force....................................... 24 2.4 The Liquid Drop Model and the Semi-Empirical Mass Formula............ 26 2.5 The Shell Model........................................ 33 2.5.1 Nuclei Configurations................................ 44 3 Radioactive Decay and Nuclear Instability 48 3.1 Radioactive Decay...................................... 49 CONTENTS CONTENTS 3.2 a Decay............................................. 56 3.2.1 Decay Mechanism and a calculation of t1/2(Q) .................. 58 3.3 b-Decay............................................. 62 3.3.1 The Valley of Stability................................ 64 3.3.2 Neutrinos, Leptons and Weak Force........................ 68 3.4 g-Decay...........................................
    [Show full text]
  • Proton and Neutron Skins and Symmetry Energy of Mirror Nuclei
    Proton and neutron skins and symmetry energy of mirror nuclei M.K. Gaidarova,∗, I. Moumeneb, A.N. Antonova, D.N. Kadreva, P. Sarrigurenc, E. Moya de Guerrad aInstitute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia 1784, Bulgaria bHigh Energy Physics and Astrophysics Laboratory, Faculty of Science Semlalia, Cadi Ayyad University, P.O.B. 2390, Marrakesh,Morocco cInstituto de Estructura de la Materia, IEM-CSIC, Serrano 123, E-28006 Madrid, Spain dDepartamento de Estructura de la Materia, F´ısicaT´ermicay Electr´onica,and IPARCOS, Facultad de Ciencias F´ısicas,Universidad Complutense de Madrid, Madrid E-28040, Spain Abstract The neutron skin of nuclei is an important fundamental property, but its accurate measurement faces many challenges. Inspired by charge symmetry of nuclear forces, the neutron skin of a neutron-rich nucleus is related to the difference between the charge radii of the corresponding mirror nuclei. We investigate this relation within the framework of the Hartree-Fock-Bogoliubov method with Skyrme interactions. Predictions for proton skins are also made for several mirror pairs in the middle mass range. For the first time the correlation between the thickness of the neutron skin and the characteristics related with the density dependence of the nuclear symme- try energy is investigated simultaneously for nuclei and their corresponding mirror partners. As an example, the Ni isotopic chain with mass number A = 48 − 60 is considered. These quan- tities are calculated within the coherent density fluctuation model using Brueckner and Skyrme energy-density functionals for isospin asymmetric nuclear matter with two Skyrme-type effective interactions, SkM* and SLy4.
    [Show full text]
  • Physics Motivation and Concepts for the Isospin Laboratory*
    Particle Accelerators, 1994, Vol. 47, pp. 111-118 @1994 Gordon and Breach Science Publishers, S.A. Reprints available directly from the publisher Printed in Malaysia Photocopying permitted by license only PHYSICS MOTIVATION AND CONCEPTS FOR THE ISOSPIN LABORATORY* J. MICHAEL NITSCHKE ISL Studies Group, Nuclear Science Division, Lawrence Berkeley Laboratory, University ofCalifornia Berkeley, California 94720, USA (Received 29 October 1993) A briefsynopsis ofthe emerging science ofradioactive nuclear beams is given. Its impact on a wide range ofstudies in nuclear structure, nuclear reaction dynamics, astrophysics, high-spin physics, nuclei far from stability, material­ and surface science, bio-medicine, and atomic- and hyperfine-interaction physics is discussed. It is pointed out that the expected low beam intensities will put stringent requirements on the performance of the accelerators and the experimental detection equipment. KEY WORDS: Radioactive nuclear beams, on-line isotope separation 1 INTRODUCTION Nuclear physics and the development ofparticle accelerators have gone hand-in-hand since the early part ofthis century. The first nuclear reaction was carried out in 1930 by Cockcroft and Walton using protons accelerated to 300keV in the reaction 7Li(p,2a). Subsequent developments progressed in two directions, heavier masses and higher energies. While heavier projectiles opened new vistas in the synthesis of new elements, the study of high spin phenomena, and the exploration ofthe nucleon drip lines, to mention only a few, higher energies allowed the study ofnuclei at higher temperatures, the equation of state ofnuclear matter, and ultimately collective phenomena resulting from the melting of the hadronic phase that may give rise to a plasma consisting of quarks and gluons.
    [Show full text]
  • Nuclei at the Limits of Particle Stability
    0» Nuclei at the limits of particle stability Alex C. Mueller Bradley M. Sherrill IPNO-DRE 9,3-10 t MSU CL 883 \ Vr - J Michigan State University National Superconducting Cyclotron Laboratory Nuclei at the limits of particle stability Alex C. Mueller Bradley M. SherriJl IPNO-DRE 93-10 MSU CL 883 Michigan State University National Superconducting Cyclotron Laboratory NUCLEI AT THE LIMITS OF PARTICLE STABILITY Alex C. Mueller CNRS-IN2P3, Institut de Physique Nucléaire, F-91406 Orsay, France and Bradley M. Sherritt National Superconducting Cyclotron Laboratoiy, Michigan State University, East Lansing, MI48824, USA KEY WORDS: nuclear ^-stability, production of unstable nuclei, on-line isotope separators and recoil spectrometers, reactions induced by unstable nuclei, properties of nuclei at the drip-lines, neutron-halo, nuclei far off stability in astrophysics Shortened Title: Exotic Nuclei (to appear in Annual Review of Nuclear and Particle Science, Volume 43) CONTENTS !.INTRODUCTION 3 2. THE LIMITS OF STABILITY 4 3. TECHNIQUES OF PRODUCTION 7 3.1 Overview 7 3.2 ISOL techniques 7 3.3 Recoil separators 9 4. PROTON-RICH NUCLEI 13 4.1 Searches for the location of the proton drip-line 13 4.2 Properties of proton rich nuclei 16 4.3 Beyond the proton drip-line 20 4.4 Astrophysics: breakout from the CNO-cvcle and the rp-process 22 4.5 Properties and synthesis of the heaviest elements 24 5. NEUTRON-RICH NUCLEI 26 5.1 Mapping of the neutron drip-line 26 5.2 Nuclear masses along the neutron drip-line 28 5.3 Decay studies 30 5.4 Nuclear moments 32 5.5 Nuclear radii, matter and charge distributions 33 5.6 Reaction studies of the halo nuclei: cross-sections, momentum distributions and neutron correlations 35 5.7 Some comments on the neutron halo.
    [Show full text]
  • The Mirror Nuclei Ga and Zn
    The Mirror Nuclei 61 Ga and 61 Zn Lise−Lotte Andersson Licentiate Thesis 2006 Department of Physics Division of Nuclear Physics Lund University LUNFD6/(NFFR−3100)/1−69/(2006) Contents Introduction 3 1 Experimental Details 5 1.1 FusionEvaporationReactions . 6 1.2 γ Detection ................................ 6 1.2.1 CLARION............................. 6 1.2.2 GAMMASPHERE ........................ 7 1.3 NeutronDetection ............................ 8 1.4 ChargedParticleDetection. 8 1.4.1 LuWUSiA............................. 8 1.4.2 Microball ............................. 9 1.5 RecoilSeparators ............................. 10 1.5.1 RecoilMassSeparator . 10 1.5.2 FragmentMassAnalyser . 11 1.6 IonisationChamber. .. .. 11 2 Data Handling 13 2.1 DataFormat ............................... 13 2.2 Handling of the γ rays .......................... 15 2.3 NeutronHandling............................. 15 2.3.1 Neutron-γ Separation....................... 16 2.3.2 Two-Neutron Event Suppression . 16 2.3.3 Neutron Identification Efficiency . 18 2.4 ChargedParticleHandling . 19 2.4.1 Proton - α Separation ...................... 19 2.5 A/Q Separation.............................. 20 2.6 IonChamberCalibrations . 20 3 Data Analysis 25 3.1 Recoil - γ Analysis ............................ 25 3.2 Recoil - γγ Analysis ........................... 26 3.3 The 61GaNucleus............................. 26 3.4 The 61ZnNucleus............................. 26 3.4.1 SpecificTransitions . 30 3.4.2 SuperdeformedBand . 37 3.5 AngularDistributionCorrections . .. 38 1 2 CONTENTS 4 Theoretical Background 41 4.1 TheShellModel.............................. 41 4.1.1 ElectromagneticTransitions . 44 4.1.2 Two-stateMixing. .. .. .. 46 4.2 Shell-Model Calculations Using the Code ANTOINE................................. 46 4.2.1 TheGXPF1andGXPF1AInteractions . 47 4.2.2 The “f5/2pg9/2”Interaction. .. .. 47 4.2.3 TheKB3GInteraction . 47 4.3 MirrorNuclei ............................... 48 5 Interpretation 51 5.1 The Shell Model Calculations . 51 5.1.1 The 61ZnNucleus........................
    [Show full text]