MGOGP: a Gene Module-Based Heuristic Algorithm for Cancer-Related Gene Prioritization Lingtao Su1,2, Guixia Liu1,2*, Tian Bai1,2*, Xiangyu Meng1,2* and Qingshan Ma3
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

A Computational Approach for Defining a Signature of Β-Cell Golgi Stress in Diabetes Mellitus
Page 1 of 781 Diabetes A Computational Approach for Defining a Signature of β-Cell Golgi Stress in Diabetes Mellitus Robert N. Bone1,6,7, Olufunmilola Oyebamiji2, Sayali Talware2, Sharmila Selvaraj2, Preethi Krishnan3,6, Farooq Syed1,6,7, Huanmei Wu2, Carmella Evans-Molina 1,3,4,5,6,7,8* Departments of 1Pediatrics, 3Medicine, 4Anatomy, Cell Biology & Physiology, 5Biochemistry & Molecular Biology, the 6Center for Diabetes & Metabolic Diseases, and the 7Herman B. Wells Center for Pediatric Research, Indiana University School of Medicine, Indianapolis, IN 46202; 2Department of BioHealth Informatics, Indiana University-Purdue University Indianapolis, Indianapolis, IN, 46202; 8Roudebush VA Medical Center, Indianapolis, IN 46202. *Corresponding Author(s): Carmella Evans-Molina, MD, PhD ([email protected]) Indiana University School of Medicine, 635 Barnhill Drive, MS 2031A, Indianapolis, IN 46202, Telephone: (317) 274-4145, Fax (317) 274-4107 Running Title: Golgi Stress Response in Diabetes Word Count: 4358 Number of Figures: 6 Keywords: Golgi apparatus stress, Islets, β cell, Type 1 diabetes, Type 2 diabetes 1 Diabetes Publish Ahead of Print, published online August 20, 2020 Diabetes Page 2 of 781 ABSTRACT The Golgi apparatus (GA) is an important site of insulin processing and granule maturation, but whether GA organelle dysfunction and GA stress are present in the diabetic β-cell has not been tested. We utilized an informatics-based approach to develop a transcriptional signature of β-cell GA stress using existing RNA sequencing and microarray datasets generated using human islets from donors with diabetes and islets where type 1(T1D) and type 2 diabetes (T2D) had been modeled ex vivo. To narrow our results to GA-specific genes, we applied a filter set of 1,030 genes accepted as GA associated. -

4-6 Weeks Old Female C57BL/6 Mice Obtained from Jackson Labs Were Used for Cell Isolation
Methods Mice: 4-6 weeks old female C57BL/6 mice obtained from Jackson labs were used for cell isolation. Female Foxp3-IRES-GFP reporter mice (1), backcrossed to B6/C57 background for 10 generations, were used for the isolation of naïve CD4 and naïve CD8 cells for the RNAseq experiments. The mice were housed in pathogen-free animal facility in the La Jolla Institute for Allergy and Immunology and were used according to protocols approved by the Institutional Animal Care and use Committee. Preparation of cells: Subsets of thymocytes were isolated by cell sorting as previously described (2), after cell surface staining using CD4 (GK1.5), CD8 (53-6.7), CD3ε (145- 2C11), CD24 (M1/69) (all from Biolegend). DP cells: CD4+CD8 int/hi; CD4 SP cells: CD4CD3 hi, CD24 int/lo; CD8 SP cells: CD8 int/hi CD4 CD3 hi, CD24 int/lo (Fig S2). Peripheral subsets were isolated after pooling spleen and lymph nodes. T cells were enriched by negative isolation using Dynabeads (Dynabeads untouched mouse T cells, 11413D, Invitrogen). After surface staining for CD4 (GK1.5), CD8 (53-6.7), CD62L (MEL-14), CD25 (PC61) and CD44 (IM7), naïve CD4+CD62L hiCD25-CD44lo and naïve CD8+CD62L hiCD25-CD44lo were obtained by sorting (BD FACS Aria). Additionally, for the RNAseq experiments, CD4 and CD8 naïve cells were isolated by sorting T cells from the Foxp3- IRES-GFP mice: CD4+CD62LhiCD25–CD44lo GFP(FOXP3)– and CD8+CD62LhiCD25– CD44lo GFP(FOXP3)– (antibodies were from Biolegend). In some cases, naïve CD4 cells were cultured in vitro under Th1 or Th2 polarizing conditions (3, 4). -

1 Supporting Information for a Microrna Network Regulates
Supporting Information for A microRNA Network Regulates Expression and Biosynthesis of CFTR and CFTR-ΔF508 Shyam Ramachandrana,b, Philip H. Karpc, Peng Jiangc, Lynda S. Ostedgaardc, Amy E. Walza, John T. Fishere, Shaf Keshavjeeh, Kim A. Lennoxi, Ashley M. Jacobii, Scott D. Rosei, Mark A. Behlkei, Michael J. Welshb,c,d,g, Yi Xingb,c,f, Paul B. McCray Jr.a,b,c Author Affiliations: Department of Pediatricsa, Interdisciplinary Program in Geneticsb, Departments of Internal Medicinec, Molecular Physiology and Biophysicsd, Anatomy and Cell Biologye, Biomedical Engineeringf, Howard Hughes Medical Instituteg, Carver College of Medicine, University of Iowa, Iowa City, IA-52242 Division of Thoracic Surgeryh, Toronto General Hospital, University Health Network, University of Toronto, Toronto, Canada-M5G 2C4 Integrated DNA Technologiesi, Coralville, IA-52241 To whom correspondence should be addressed: Email: [email protected] (M.J.W.); yi- [email protected] (Y.X.); Email: [email protected] (P.B.M.) This PDF file includes: Materials and Methods References Fig. S1. miR-138 regulates SIN3A in a dose-dependent and site-specific manner. Fig. S2. miR-138 regulates endogenous SIN3A protein expression. Fig. S3. miR-138 regulates endogenous CFTR protein expression in Calu-3 cells. Fig. S4. miR-138 regulates endogenous CFTR protein expression in primary human airway epithelia. Fig. S5. miR-138 regulates CFTR expression in HeLa cells. Fig. S6. miR-138 regulates CFTR expression in HEK293T cells. Fig. S7. HeLa cells exhibit CFTR channel activity. Fig. S8. miR-138 improves CFTR processing. Fig. S9. miR-138 improves CFTR-ΔF508 processing. Fig. S10. SIN3A inhibition yields partial rescue of Cl- transport in CF epithelia. -

Analysis of the Dynamics of Limb Transcriptomes During Mouse Development Istvan Gyurján1, Bernhard Sonderegger1, Felix Naef1,2 and Denis Duboule1,3*
Gyurján et al. BMC Developmental Biology 2011, 11:47 http://www.biomedcentral.com/1471-213X/11/47 RESEARCH ARTICLE Open Access Analysis of the dynamics of limb transcriptomes during mouse development Istvan Gyurján1, Bernhard Sonderegger1, Felix Naef1,2 and Denis Duboule1,3* Abstract Background: The development of vertebrate limbs has been a traditional system to study fundamental processes at work during ontogenesis, such as the establishment of spatial cellular coordinates, the effect of diffusible morphogenetic molecules or the translation between gene activity and morphogenesis. In addition, limbs are amongst the first targets of malformations in human and they display a huge realm of evolutionary variations within tetrapods, which make them a paradigm to study the regulatory genome. Results: As a reference resource for future biochemical and genetic analyses, we used genome-wide tiling arrays to establish the transcriptomes of mouse limb buds at three different stages, during which major developmental events take place. We compare the three time-points and discuss some aspects of these datasets, for instance related to transcriptome dynamics or to the potential association between active genes and the distribution of intergenic transcriptional activity. Conclusions: These datasets provide a valuable resource, either for research projects involving gene expression and regulation in developing mouse limbs, or as examples of tissue-specific, genome-wide transcriptional activities. Background regulators of the dorso-ventral (DV) patterning are Limb development has fascinated biologists for a cen- Wnt7a, expressed in dorsal ectoderm, and Engrailed,in tury, mostly because of the importance of these struc- ventral ectoderm, as well as Lmxb1,agenetranscribed tures in the evolution of land vertebrates and due to in dorsal mesenchyme. -

Genome‑Wide Investigation of the Clinical Implications and Molecular Mechanism of Long Noncoding RNA LINC00668 and Protein‑Coding Genes in Hepatocellular Carcinoma
860 INTERNATIONAL JOURNAL OF ONCOLOGY 55: 860-878 2019 Genome‑wide investigation of the clinical implications and molecular mechanism of long noncoding RNA LINC00668 and protein‑coding genes in hepatocellular carcinoma XIANGKUN WANG1, XIN ZHOU1, JUNQI LIU1, ZHENGQIAN LIU1, LINBO ZHANG2, YIZHEN GONG3, JIANLU HUANG4, LONG YU1,5, QIAOQI WANG6, CHENGKUN YANG1, XIWEN LIAO1, TINGDONG YU1, CHUANGYE HAN1, GUANGZHI ZHU1, XINPING YE1 and TAO PENG1 Department of 1Hepatobiliary Surgery, 2Health Management and Division of Physical Examination and 3Colorectal and Anal Surgery, The First Affiliated Hospital of Guangxi Medical University, Nanning, Guangxi Zhuang Autonomous Region 530021; 4Department of Hepatobiliary Surgery, Third Affiliated Hospital of Guangxi Medical University, Nanning, Guangxi Zhuang Autonomous Region 530031; 5Department of Hepatobiliary and Pancreatic Surgery, The First Affiliated Hospital of Zhengzhou University, Zhengzhou, Henan 450000; 6Department of Medical Cosmetology, The Second Affiliated Hospital of Guangxi Medical University, Nanning, Guangxi Zhuang Autonomous Region 530000, P.R. China Received April 12, 2019; Accepted July 31, 2019 DOI: 10.3892/ijo.2019.4858 Abstract. Hepatocellular carcinoma (HCC) is one of the clinical factors and PCGs were used to construct a nomo- leading causes of tumor-related mortalities worldwide. gram for predicting prognosis in HCC. A Connectivity Map Long noncoding RNAs have been reported to be associ- was constructed to identify candidate target drugs for HCC. ated with tumor initiation, progression and prognosis. The The top 10 PCGs identified were: Pyrimidineregic receptor present study aimed to explore the association between long P2Y4 (P2RY4), signal peptidase complex subunit 2 (SPCS2), noncoding RNA LINC00668 and its co-expression correlated family with sequence similarity 86 member C1 (FAM86C1), protein-coding genes (PCGs) in HCC. -

CPTC-CDK1-1 (CAB079974) Immunohistochemistry
CPTC-CDK1-1 (CAB079974) Uniprot ID: P06493 Protein name: CDK1_HUMAN Full name: Cyclin-dependent kinase 1 Tissue specificity: Isoform 2 is found in breast cancer tissues. Function: Plays a key role in the control of the eukaryotic cell cycle by modulating the centrosome cycle as well as mitotic onset; promotes G2-M transition, and regulates G1 progress and G1-S transition via association with multiple interphase cyclins. Required in higher cells for entry into S-phase and mitosis. Phosphorylates PARVA/actopaxin, APC, AMPH, APC, BARD1, Bcl-xL/BCL2L1, BRCA2, CALD1, CASP8, CDC7, CDC20, CDC25A, CDC25C, CC2D1A, CENPA, CSNK2 proteins/CKII, FZR1/CDH1, CDK7, CEBPB, CHAMP1, DMD/dystrophin, EEF1 proteins/EF-1, EZH2, KIF11/EG5, EGFR, FANCG, FOS, GFAP, GOLGA2/GM130, GRASP1, UBE2A/hHR6A, HIST1H1 proteins/histone H1, HMGA1, HIVEP3/KRC, LMNA, LMNB, LMNC, LBR, LATS1, MAP1B, MAP4, MARCKS, MCM2, MCM4, MKLP1, MYB, NEFH, NFIC, NPC/nuclear pore complex, PITPNM1/NIR2, NPM1, NCL, NUCKS1, NPM1/numatrin, ORC1, PRKAR2A, EEF1E1/p18, EIF3F/p47, p53/TP53, NONO/p54NRB, PAPOLA, PLEC/plectin, RB1, TPPP, UL40/R2, RAB4A, RAP1GAP, RCC1, RPS6KB1/S6K1, KHDRBS1/SAM68, ESPL1, SKI, BIRC5/survivin, STIP1, TEX14, beta-tubulins, MAPT/TAU, NEDD1, VIM/vimentin, TK1, FOXO1, RUNX1/AML1, SAMHD1, SIRT2 and RUNX2. CDK1/CDC2-cyclin-B controls pronuclear union in interphase fertilized eggs. Essential for early stages of embryonic development. During G2 and early mitosis, CDC25A/B/C-mediated dephosphorylation activates CDK1/cyclin complexes which phosphorylate several substrates that trigger at least centrosome separation, Golgi dynamics, nuclear envelope breakdown and chromosome condensation. Once chromosomes are condensed and aligned at the metaphase plate, CDK1 activity is switched off by WEE1- and PKMYT1-mediated phosphorylation to allow sister chromatid separation, chromosome decondensation, reformation of the nuclear envelope and cytokinesis. -

Mutations in Disordered Regions Cause Disease by Creating Endocytosis Motifs
bioRxiv preprint doi: https://doi.org/10.1101/141622; this version posted May 24, 2017. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. Mutations in disordered regions cause disease by creating endocytosis motifs Katrina Meyer1, Bora Uyar2, Marieluise Kirchner3, Jingyuan Cheng1, Altuna Akalin2, Matthias Selbach1,4 1 Proteome Dynamics, Max Delbrück Center for Molecular Medicine, Robert-Rössle-Str. 10, D-13092 Berlin, Germany 2 Bioinformatics Platform, Max Delbrück Center for Molecular Medicine, Robert-Rössle- Str. 10, D-13092 Berlin, Germany 3 BIH Core Facility Proteomics, Robert-Rössle-Str. 10, D-13092 Berlin, Germany 4 Charité-Universitätsmedizin Berlin, 10117 Berlin, Germany Corresponding author: Matthias Selbach Max Delbrück Centrum for Molecular Medicine Robert-Rössle-Str. 10, D-13092 Berlin, Germany Tel.: +49 30 9406 3574 Fax.: +49 30 9406 2394 email: [email protected] Word count: 2741 bioRxiv preprint doi: https://doi.org/10.1101/141622; this version posted May 24, 2017. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. 1 Abstract 2 Mutations in intrinsically disordered regions (IDRs) of proteins can cause a wide 3 spectrum of diseases. Since IDRs lack a fixed three-dimensional structure, the 4 mechanism by which such mutations cause disease is often unknown. Here, we employ 5 a proteomic screen to investigate the impact of mutations in IDRs on protein-protein 6 interactions. We find that mutations in disordered cytosolic regions of three 7 transmembrane proteins (GLUT1, ITPR1 and CACNA1H) lead to an increased binding 8 of clathrins. -

Identification of Differentially Expressed Genes in Human Bladder Cancer Through Genome-Wide Gene Expression Profiling
521-531 24/7/06 18:28 Page 521 ONCOLOGY REPORTS 16: 521-531, 2006 521 Identification of differentially expressed genes in human bladder cancer through genome-wide gene expression profiling KAZUMORI KAWAKAMI1,3, HIDEKI ENOKIDA1, TOKUSHI TACHIWADA1, TAKENARI GOTANDA1, KENGO TSUNEYOSHI1, HIROYUKI KUBO1, KENRYU NISHIYAMA1, MASAKI TAKIGUCHI2, MASAYUKI NAKAGAWA1 and NAOHIKO SEKI3 1Department of Urology, Graduate School of Medical and Dental Sciences, Kagoshima University, 8-35-1 Sakuragaoka, Kagoshima 890-8520; Departments of 2Biochemistry and Genetics, and 3Functional Genomics, Graduate School of Medicine, Chiba University, 1-8-1 Inohana, Chuo-ku, Chiba 260-8670, Japan Received February 15, 2006; Accepted April 27, 2006 Abstract. Large-scale gene expression profiling is an effective CKS2 gene not only as a potential biomarker for diagnosing, strategy for understanding the progression of bladder cancer but also for staging human BC. This is the first report (BC). The aim of this study was to identify genes that are demonstrating that CKS2 expression is strongly correlated expressed differently in the course of BC progression and to with the progression of human BC. establish new biomarkers for BC. Specimens from 21 patients with pathologically confirmed superficial (n=10) or Introduction invasive (n=11) BC and 4 normal bladder samples were studied; samples from 14 of the 21 BC samples were subjected Bladder cancer (BC) is among the 5 most common to microarray analysis. The validity of the microarray results malignancies worldwide, and the 2nd most common tumor of was verified by real-time RT-PCR. Of the 136 up-regulated the genitourinary tract and the 2nd most common cause of genes we detected, 21 were present in all 14 BCs examined death in patients with cancer of the urinary tract (1-7). -

Investigation of Differentially Expressed Genes in Nasopharyngeal Carcinoma by Integrated Bioinformatics Analysis
916 ONCOLOGY LETTERS 18: 916-926, 2019 Investigation of differentially expressed genes in nasopharyngeal carcinoma by integrated bioinformatics analysis ZhENNING ZOU1*, SIYUAN GAN1*, ShUGUANG LIU2, RUjIA LI1 and jIAN hUANG1 1Department of Pathology, Guangdong Medical University, Zhanjiang, Guangdong 524023; 2Department of Pathology, The Eighth Affiliated hospital of Sun Yat‑sen University, Shenzhen, Guangdong 518033, P.R. China Received October 9, 2018; Accepted April 10, 2019 DOI: 10.3892/ol.2019.10382 Abstract. Nasopharyngeal carcinoma (NPC) is a common topoisomerase 2α and TPX2 microtubule nucleation factor), malignancy of the head and neck. The aim of the present study 8 modules, and 14 TFs were identified. Modules analysis was to conduct an integrated bioinformatics analysis of differ- revealed that cyclin-dependent kinase 1 and exportin 1 were entially expressed genes (DEGs) and to explore the molecular involved in the pathway of Epstein‑Barr virus infection. In mechanisms of NPC. Two profiling datasets, GSE12452 and summary, the hub genes, key modules and TFs identified in GSE34573, were downloaded from the Gene Expression this study may promote our understanding of the pathogenesis Omnibus database and included 44 NPC specimens and of NPC and require further in-depth investigation. 13 normal nasopharyngeal tissues. R software was used to identify the DEGs between NPC and normal nasopharyngeal Introduction tissues. Distributions of DEGs in chromosomes were explored based on the annotation file and the CYTOBAND database Nasopharyngeal carcinoma (NPC) is a common malignancy of DAVID. Gene ontology (GO) and Kyoto Encyclopedia of occurring in the head and neck. It is prevalent in the eastern Genes and Genomes (KEGG) pathway enrichment analysis and southeastern parts of Asia, especially in southern China, were applied. -
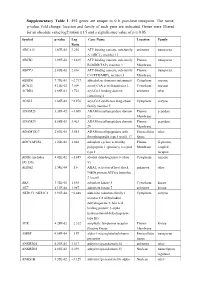
Supplementary Table 1
Supplementary Table 1. 492 genes are unique to 0 h post-heat timepoint. The name, p-value, fold change, location and family of each gene are indicated. Genes were filtered for an absolute value log2 ration 1.5 and a significance value of p ≤ 0.05. Symbol p-value Log Gene Name Location Family Ratio ABCA13 1.87E-02 3.292 ATP-binding cassette, sub-family unknown transporter A (ABC1), member 13 ABCB1 1.93E-02 −1.819 ATP-binding cassette, sub-family Plasma transporter B (MDR/TAP), member 1 Membrane ABCC3 2.83E-02 2.016 ATP-binding cassette, sub-family Plasma transporter C (CFTR/MRP), member 3 Membrane ABHD6 7.79E-03 −2.717 abhydrolase domain containing 6 Cytoplasm enzyme ACAT1 4.10E-02 3.009 acetyl-CoA acetyltransferase 1 Cytoplasm enzyme ACBD4 2.66E-03 1.722 acyl-CoA binding domain unknown other containing 4 ACSL5 1.86E-02 −2.876 acyl-CoA synthetase long-chain Cytoplasm enzyme family member 5 ADAM23 3.33E-02 −3.008 ADAM metallopeptidase domain Plasma peptidase 23 Membrane ADAM29 5.58E-03 3.463 ADAM metallopeptidase domain Plasma peptidase 29 Membrane ADAMTS17 2.67E-04 3.051 ADAM metallopeptidase with Extracellular other thrombospondin type 1 motif, 17 Space ADCYAP1R1 1.20E-02 1.848 adenylate cyclase activating Plasma G-protein polypeptide 1 (pituitary) receptor Membrane coupled type I receptor ADH6 (includes 4.02E-02 −1.845 alcohol dehydrogenase 6 (class Cytoplasm enzyme EG:130) V) AHSA2 1.54E-04 −1.6 AHA1, activator of heat shock unknown other 90kDa protein ATPase homolog 2 (yeast) AK5 3.32E-02 1.658 adenylate kinase 5 Cytoplasm kinase AK7 -

Blood-Derived Mitochondrial DNA Copy Number Is Associated with Gene Expression Across Multiple
bioRxiv preprint doi: https://doi.org/10.1101/2020.07.17.209023; this version posted July 18, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. 1 Blood-derived mitochondrial DNA copy number is associated with gene expression across multiple 2 tissues and is predictive for incident neurodegenerative disease 3 4 Stephanie Y. Yang1, Christina A. Castellani1, Ryan J. Longchamps1, Vamsee K. Pillalamarri1, Brian 5 O’Rourke2, Eliseo Guallar3, Dan E. Arking1,2 6 7 8 1McKusick-Nathans Department of Genetic Medicine, Johns Hopkins University School of Medicine, 9 Baltimore, MD 10 2Division of Cardiology, Department of Medicine, Johns Hopkins University School of Medicine, 11 Baltimore, MD 12 3Departments of Epidemiology and Medicine, and Welch Center for Prevention, Epidemiology, and 13 Clinical Research, Johns Hopkins University Bloomberg School of Public Health, Baltimore, MD 14 15 Email addresses: 16 [email protected] 17 [email protected] 18 [email protected] 19 [email protected] 20 [email protected] 21 [email protected] 22 [email protected] 23 24 25 26 27 28 29 30 31 32 33 34 35 *Correspondence and address for reprints to: 36 Dan E. Arking, Ph.D. 37 Johns Hopkins University School of Medicine 38 733 N Broadway Ave 39 Miller Research Building Room 459 40 Baltimore, MD 21205 41 (410) 502-4867 (ph) 42 [email protected] 1 bioRxiv preprint doi: https://doi.org/10.1101/2020.07.17.209023; this version posted July 18, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. -

Cisgenome User's Manual 1. Overview 1.1 Basic Framework Of
CisGenome User’s Manual 1. Overview 1.1 Basic Framework of CisGenome 1.2 Installation 1.3 Summary of All Functions 1.4 A Quick Start – Analysis of a ChIP-chip Experiment 2. Genomics Toolbox I – Establishing Local Genome Databases 2.1 Introduction to Local Genome Database 2.2 List of Functions 2.3 Establishing Database Step I – Download Sequences and Annotation 2.4 Establishing Database Step II – Coding Genome Sequences 2.5 Establishing Database Step III – Coding Gene Annotations 2.6 Establishing Database Step IV – Creating Markov Background 2.7 Establishing Database Step V – Coding Conservation Scores 2.8 Establishing Database Step VI – Creating Coding Region Indicators 3. Genomics Toolbox II – Sequence and Conservation Score Retrieval 3.1 Introduction 3.2 List of Functions 3.3 Sequence Manipulation I – Retrieving Sequences for Specified Genomic Regions. 3.4 Sequence Manipulation II – Retrieving Sequences and Conservation Scores for Specified Genomic Regions 3.5 Sequence Manipulation III – Retrieving Sequences in which Protein Coding Regions and/or Non-Conserved Regions are masked. 3.6 Sequence Manipulation IV – Filtering Genomic Regions according to Repeats, Conservation Scores and CDS Status. 3.7 Sequence Manipulation V – Masking Certain Regions from FASTA Sequences. 4. Genomics Toolbox III – Obtaining Annotations and Orthologs For Specified Regions 4.1 Introduction 4.2 List of Functions 4.3 Getting Base Occurrence Frequencies and Conservation Score Distributions for Specified Genomic Regions 4.4 Associating Genomic Regions with Neighboring Genes 4.5 Getting Regions Surrounding Transcriptional Starts 4.6 Getting Affymetrix Probeset IDs for Specified Genes 4.7 Identifying Ortholog (Homolog) Genes 5.