Sample Size Debate
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
Schools Want Students to PASS on Vaping
MONDAY, FEBRUARY 25, 2019 STEVE KRAUSE COMMENTARY Schools Playoffs at 4-16? There’s a better way. want The Massachusetts high school I want to focus on one particularly similarity to the elevated strato- tournament pairings in hockey and potential gross mismatch to prove my sphere of the Dukes and Villanovas. basketball are out, and, once again, point about basketball. They are basically cannon fodder for students the ridiculous things about them just A 4-16 Saugus basketball team the big boys to loosen up and make jump out at you. sneaked in with the 16th seed in Divi- sure their shoes are in working or- There’s nothing so astonishingly sion 3 North, and will play at No. 1 St. der (have to say that now after the to PASS stupid as a zero-win football team go- Mary’s Tuesday. Zion Williamson asco last week). ing to the postseason playoffs while Now, we’ve seen some pretty But when the pairings come out next a 4-3 Classical team is left out. That one-sided 1-16 games in the NCAAs, month, notice the records of those happened in the fall, and it illustrates but I can assure you the 16s are the play-in schools and the 16 seeds. All on vaping how futile it is to give everybody a tro- big sh in little ponds. They are al- of them are worthy. phy in a sport that just isn’t set up for most always 20-win teams that play By Gayla Cawley that kind of a tournament. -

2020 Major League Baseball Spring Training Media Guide
2020 MAJOR LEAGUE BASEBALL SPRING TRAINING MEDIA GUIDE CACTUS LEAGUE GRAPEFRUIT LEAGUE Arizona Diamondbacks ............................. 3-7 Atlanta Braves ....................................... 85-90 Chicago Cubs .......................................... 8-13 Baltimore Orioles .................................. 91-96 Chicago White Sox ............................... 14-19 Boston Red Sox ................................... 97-102 Cincinnati Reds .................................... 20-25 Detroit Tigers .................................... 103-108 Cleveland Indians .................................. 26-31 Houston Astros ................................. 109-113 Colorado Rockies .................................. 32-37 Miami Marlins .................................. 114-118 Kansas City Royals ................................ 38-42 Minnesota Twins ............................... 119-123 Los Angeles Angels ................................ 43-48 New York Mets .................................. 124-128 Los Angeles Dodgers ............................. 49-53 New York Yankees ............................. 129-133 Milwaukee Brewers ............................... 54-58 Philadelphia Phillies .......................... 134-138 Oakland Athletics .................................. 59-64 Pittsburgh Pirates .............................. 139-144 San Diego Padres ................................... 65-69 St. Louis Cardinals ............................ 145-149 San Francisco Giants ............................. 70-74 Tampa Bay Rays ............................... -

2018 Sun Devil Baseball 2018 Roster
2018 Sun Devil Baseball 2018 Roster 2018 Sun Devil Baseball Five -Time NCAA Champions (1965, 1967, 1969, 1977, 1981) | 22 College World Series Appearances | 21 Conference Championships TWITTER: @ASU_BASEBALL 123 All-Americans | 14 National Players of the Year | 10 College Baseball Hall of Fame Members INSTAGRAM: @ASU_BASEBALL 1 414 Major League Baseball Draft Picks | 108 Major Leaguers | 49 Major League Baseball First-Round Draft Picks FACEBOOK: SUNDEVILBASEBALL 2018 ROSTER PITCHERS (16) No. Name YR B/T HT WT Hometown (High School/Last School) 30 Brady Corrigan Fr. R/R 6’2” 200 Plainfield, Ill. (Plainfield North) 36 Colby Davis Fr. R/R 6’8” 225 Scottsdale, Ariz. (Chaparral) 31 Drake Davis Fr. R/R 6’0” 185 Highlands Ranch, Colo. (Ralston Valley) 23 Jake Godfrey Sr. R/R 6’3” 225 New Lenox, Ill. (Providence Catholic/LSU/NW Florida St.) 11 Connor Higgins Jr. R/L 6’5” 240 Orefield, Pa. (Parkland) 17 Ryan Hingst Sr. R/R 6’4” 191 El Paso, Texas (Franklin) 15 Eli Lingos Sr. L/L 6’0” 192 Temecula, Calif. (Great Oak) 8 Alec Marsh So. R/R 6’2” 220 Milwaukee, Wis. (Ronald Reagan) 3 Chaz Montoya So. L/L 6’0” 160 Glendale, Ariz. (Centennial) 41 Dellan Raish R-Fr. L/L 6’2” 180 Cave Creek, Ariz. (Cactus Shadows) 26 Sam Romero Jr. R/R 6’2” 180 Phoenix, Ariz. (Carl Hayden/Phoenix College) 29 Grant Schneider Sr. R/R 6’3” 205 Austin, Texas (Lake Travis) 22 Fitz Stadler Jr. R/R 6’9” 240 Glenbrook, Ill. (Glenbrook South) 25 Zane Strand R-Fr. -

BOSTON RED SOX (93-43) at CHICAGO WHITE SOX (54-81) Saturday, September 1, 2018 • 6:10 P.M
WORLD SERIES CHAMPIONS (8): 1903, 1912, 1915, 1916, 1918, 2004, 2007, 2013 AMERICAN LEAGUE CHAMPIONS (13): 1903, 1904, 1912, 1915, 1916, 1918, 1946, 1967, 1975, 1986, 2004, 2007, 2013 AMERICAN LEAGUE EAST DIVISION CHAMPIONS (9): 1975, 1986, 1988, 1990, 1995, 2007, 2013, 2016, 2017 AMERICAN LEAGUE WILD CARD (7): 1998, 1999, 2003, 2004, 2005, 2008, 2009 @BOSTONREDSOXPR • HTTP://PRESSROOM.REDSOX.COM • @SOXNOTES BOSTON RED SOX (93-43) at CHICAGO WHITE SOX (54-81) Saturday, September 1, 2018 • 6:10 p.m. CT/7:10 p.m. ET • Guaranteed Rate Field • Chicago, IL LHP Eduardo Rodriguez (11-3, 3.44) vs. LHP Carlos Rodón (6-3, 2.70) Game #137 • Road Game #71 • TV: NESN • Radio: WEEI 93.7 FM, WCCM 1490 AM/103.7 FM (Spanish) STATE OF THE SOX: The Red Sox lead the majors with 93 MONTH BY MONTH: The Red Sox have posted a .620+ wins and a .684 win %...With 26 games remaining, they winning percentage in each month of the season: March REGULAR SEASON BREAKDOWN AL East Standing ...........................1st, +7.5 have already matched their win totals from 2016 and 2017. (2-1, .667), April (19-6, .760), May (18-11, .621), June Home/Road ............................. 48-18/45-25 The Sox’ magic number to clinch a playoff berth is 10. (17-10, .630), July (19-6, .760), and August (18-9, .667). Day/Night .................................. 30-7/63-36 BOS and HOU own MLB’s highest run differential (+215). The only season in which BOS has ever had a .620+ March/April/May .................2-1/19-6/18-11 June/July/August ...............17-10/19-6/18-9 win % in each month is 1912. -
July 20, 1969. One Small Step for Man
DEALS OF THE $DAY$ PG. 2 SATURDAY, JULY 20, 2019 July 20, 1969. One small step for man. OPINION ...................................A4 LOOK! .......................................A8 DIVERSIONS .............................B5 HIGH 98° VOL. 141, ISSUE 189 POLICE/FIRE .............................A6 SPORTS ................................ B1-3 CLASSIFIED ...............................B7 LOW 82° REAL ESTATE .............................A7 COMICS ....................................B4 PAGE A8 ONE DOLLAR A2 THE DAILY ITEM SATURDAY, JULY 20, 2019 Wheelabrator Saugus may have to pay up By Bridget Turcotte escaping steam, but neigh- willfully, negligently, or have a hearing to rescind, “Wheelabrator operates noise before they took ITEM STAFF bors compared the noise to through failure to provide suspend, or modify a fa- in compliance with all per- that turine to get it re- a plane constantly flying necessary equipment, ser- cility’s site assignment if mits as well as all federal, furbished,” said Panetta. SAUGUS — Wheela- overhead. After 10 days, vice, or maintenance, or to “operations at the facility state, and local environ- “They should have com- brator Saugus could face the plant shut down oper- take necessary precautions have resulted in a threat mental and public health municated that game plan fines of up to $600,000 for ations for three days un- cause, suffer, allow, or per- to public health, safety, regulations, which are with the Board of Health.” alleged noise regulation til an enhanced silencer mit necessary emissions and the environment.” among the most stringent Wheelabrator should be violations. could be installed. from said source of sound Finally, there is a Board of any industry,” said Na- held accountable for what The Saugus Board of But neighbors, includ- that may cause noise.” of Health regulation deau in an email. -

Boston Red Sox Spring Training Game Notes
BOSTON RED SOX SPRING TRAINING GAME NOTES Boston Red Sox (6-10) vs. Minnesota Twins (8-7-1) • 1:05 p.m. • JetBlue Park, Lee County, FL Boston Red Sox (6-10) at Tampa Bay Rays (7-9) • 1:05 p.m. • Charlotte Sports Park, Port Charlotte, FL GRAPEFRUIT STATUS: Today the Red Sox continue their WORLDLY PARTICIPATION: Red Sox minor league RHPs MEDIA GUIDE: The 2016 Boston Red Grapefruit League slate with both a home game against the William Cuevas (Colombia) and Jhonny Polanco (Nicara- Twins and a road game at the Rays...These are the 17th and gua) are participating in World Baseball Classic qualifi ers Sox Media Guide is available for down- 18th contests in a stretch of 31 Grapefruit League games through Sunday...Walter Miranda, pitching coach for the load at http://pressroom.redsox.com. over 30 days from March 2-31...The Sox conclude their ex- Single-A Greenville Drive, is on Colombia’s coaching staff. Members of the media may see a mem- hibition schedule with 2 additional games against Toronto ber of the Red Sox Media Relations De- in Montreal from April 1-2. ROSTER MOVES: Prior to today’s games, the Red Sox partment to request a print copy. optioned INF Marco Hernandez to Triple-A Pawtucket and Boston’s only off-day from today until the last of 2 reassigned RHP Kyle Martin to minor league camp. games in Montreal comes on March 23. With these moves, the Red Sox now have 46 players IN CAMP: Boston has 46 players in Boston opens the regular season on April 4 at CLE and in big league camp, including 34 players from the 40- Major League Spring Training Camp, plays its fi rst home game on April 11 vs. -
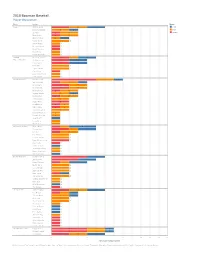
18 Bowman Team + Player
2018 Bowman Baseball Player Breakdown Team Player Group Angels® Jahmai Jones 2 2 2 Auto Chris Rodriguez 2 1 Base Jo Adell 1 2 Insert Matt Thaiss 1 2 Shohei Ohtani 1 1 Taylor Ward 2 Albert Pujols 1 Brandon Marsh 1 David Fletcher 1 Mike Trout 1 Parker Bridwell 1 Arizona Anthony Banda 2 1 2 Diamondbacks® Jon Duplantier 2 2 Pavin Smith 2 2 Drew Ellis 2 Taylor Clarke 2 Alex Young 1 Paul Goldschmidt 1 Zack Greinke 1 Atlanta Braves™ Ronald Acuna 5 2 1 Ian Anderson 1 2 1 Kyle Wright 2 2 Mike Soroka 2 2 Bryse Wilson 1 2 Cristian Pache 2 1 Kolby Allard 1 2 Alex Jackson 2 Austin Riley 2 Luiz Gohara 1 1 Ozzie Albies 1 1 Touki Toussaint 2 Dansby Swanson 1 Freddie Freeman 1 Joey Wentz 1 Lucas Sims 1 Max Fried 1 Baltimore Orioles® Austin Hays 1 1 3 Chance Sisco 2 1 2 D.L. Hall 1 2 D.J. Stewart 2 Hunter Harvey 2 Ryan Mountcastle 2 Alex Wells 1 Cedric Mullins 1 Jonathan Schoop 1 Manny Machado 1 Matthias Dietz 1 Boston Red Sox® Michael Chavis 4 2 Jay Groome 3 2 Rafael Devers 1 1 2 Bryan Mata 2 C.J. Chatham 2 Josh Ockimey 2 Sam Travis 1 1 Travis Lakins 2 Andrew Benintendi 1 Chris Sale 1 Mike Shawaryn 1 Tzu-Wei Lin 1 Chicago Cubs® Adbert Alzolay 2 2 2 Kris Bryant 1 1 1 Thomas Hatch 2 1 Alex Lange 2 Oscar De La Cruz 2 Anthony Rizzo 1 Charcer Burks 1 David Bote 1 Erich Uelman 1 Jen-Ho Tseng 1 Jose Albertos 1 Kyle Schwarber 1 Mark Zagunis 1 Victor Caratini 1 Chicago White Sox® Eloy Jimenez 4 2 1 Michael Kopech 4 2 1 Luis Robert 2 2 2 Dane Dunning 0 1 1 2 3 4 5 6 7 8 9 10 11 12 13 # of unique cards per player Distinct count of Set Name for each Player broken down by Team. -

AUGUST 8Th PAWTUCKET (52-60) at LOUISVILLE (50-61) 7:05 Pm
AUGUST 8th PAWTUCKET (52-60) at LOUISVILLE (50-61) 7:05 pm Pawtucket Red Sox RHP Chandler Shepherd (6-7, 3.91) vs. Louisville Bats LHP Cody Reed (4-8, 4.06) Late Summer Trip to Kentucky – This week, the Pawtucket Red Sox pay their only visit of the season to the great State of Kentucky when they take on the Louisville Bats in a series that continues tonight at 7:05 p.m. at Louisville Slugger Field. The PawSox usually make their only sojourn to Louisville either early in the season or by mid-season, but in a scheduling rarity they have now landed in Kentucky in August last year and this year. Following Tuesday’s 3-2 Pawtucket win in the opener, the Sox and Bats play tonight and tomorrow night (both at 7:05 p.m.) before Pawtucket moves on to Indianapolis for a 3-game weekend series vs. the Indians on Friday (7:15 pm), Saturday (7:05 pm), and Sunday (1:35 pm) at Victory Field in downtown Indy. Pawtucket — who has lost 9 of their last 11 road games dating back to July 17 — will return to McCoy on Monday for a 7-game homestand from August 13-19 (three vs. Norfolk and four vs. Durham). When Last We Met – Pawtucket took 2 of 3 at home vs. Louisville two months ago when the teams met for the only other time this season from June 5-7 at McCoy Stadium. In the series opener, the Bats scored 3 runs in the top of the 9th to win, 7-4. -
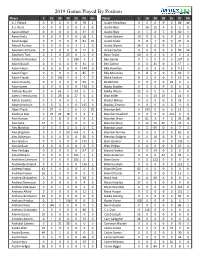
2019 Games Played by Position Player C 1B 2B 3B SS of DH Player C 1B 2B 3B SS of DH A.J
2019 Games Played By Position Player C 1B 2B 3B SS OF DH Player C 1B 2B 3B SS OF DH A.J. Pollock 0 0 0 0 0 79 1 Austin Meadows 0 0 0 0 0 88 44 A.J. Reed 0 4 0 0 0 0 9 Austin Nola 7 58 15 4 0 2 0 Aaron Altherr 0 0 0 0 0 31 0 Austin Riley 0 5 0 5 0 60 1 Aaron Hicks 0 0 0 0 0 58 1 Austin Romine 70 0 0 0 0 0 0 Aaron Judge 0 0 0 0 0 91 10 Austin Slater 0 8 1 0 0 47 0 Abiatal Avelino 0 0 0 0 1 1 0 Austin Wynns 24 0 0 0 0 0 1 Abraham Almonte 0 0 0 0 0 12 0 Avisail Garcia 0 0 0 0 0 99 24 Abraham Toro 0 1 0 23 0 0 0 Beau Taylor 10 0 0 0 0 0 0 Adalberto Mondesi 0 0 0 0 100 0 2 Ben Gamel 0 0 0 0 0 107 0 Adam Duvall 0 0 0 0 0 31 0 Ben Zobrist 0 0 31 0 0 17 1 Adam Eaton 0 0 0 0 0 144 0 Billy Hamilton 0 0 0 0 0 113 1 Adam Engel 0 0 0 0 0 85 0 Billy Mckinney 0 8 0 0 0 69 3 Adam Frazier 0 0 141 0 0 0 0 Blake Swihart 8 2 0 0 0 19 0 Adam Haseley 0 0 0 0 0 64 0 Bo Bichette 0 0 0 0 42 0 4 Adam Jones 0 0 0 0 0 130 0 Bobby Bradley 0 5 0 0 0 0 8 Addison Russell 0 0 63 0 20 0 0 Bobby Wilson 15 0 0 0 0 0 0 Adeiny Hechavarria 0 0 29 8 27 0 1 Brad Miller 0 0 13 19 1 16 0 Adrian Sanchez 0 1 4 5 2 1 0 Braden Bishop 0 0 0 0 0 23 1 Albert Almora Jr. -
World Series Opener
tONiGht: Mostly Clear. Low of 59. Search for The Westfield News The WestfieldNews Search“E for DUCATIONThe Westfield NewsIS A PRIVATE Westfield350.com The WestfieldNews MATTER BETWeeN THE Serving Westfield, Southwick, and surrounding Hilltowns P“TERSONIME IS ANDTHE ONLYTHE WORLD OF WEATHER KNOWLCRITICEDGE WITHOUT AND EXP ERIENCE, TONIGHT ANDAMBITION HAS LITTL.” E TO DO Partly Cloudy. WITH SCHOOLJOHN STEINBECK OR COLLEGE.” Low of 55. www.thewestfieldnews.com Search for The Westfield News Westfield350.comWestfield350.org The WestfieldNews — LiLLiaN Smith “TIME IS THE ONLY VOL. 86 NO. 151 Serving Westfield, Southwick, and surrounding Hilltowns WEATHER TUESDAY, JUNE 27, 2017 75 centsCRITIC WITHOUT VOL. 88 NO. 187 FRIDAY, AUGUST 9, 2019 75 Cents TONIGHT AMBITION.” Partly Cloudy. JOHN STEINBECK Low of 55. www.thewestfieldnews.com VOL.Burglar 86 NO. 151 TUESDAY, JUNE 27, 2017 Firefighter 75 cents convicted, replacement strategy jailed By CARL E. HARTDEGEN approved Correspondent WESTFIELD – A Green Avenue By HOPE E. TREMBLAY resident with a history with city Correspondent police has been sent to jail for a WESTFIELD – The Westfield Fire year after pleading guilty to his Commission this week approved Fire most recent infraction, a nighttime Chief Patrick Egloff’s plan to replace burglary of a neighbor’s home open firefighter positions. while the residents were sleeping. By the end of August there will be Michael R. Hiltbrand, 47, of 5 three vacant positions, and because Green Ave., Westfield, pleaded Egloff requires all new firefighters to guilty in Westfield District Court also be paramedics, the available Wednesday to charges of larceny pool of applicants is slim. In fact, from a building and breaking and Egloff said there are no civil service entering a building in the nighttime candidates who are currently both a with intent to commit a felony. -

2015 AFL Game Notes
2015 AFL Game Notes Thursday, October 15, 2015 Media Relations: Paul Jensen (480) 710-8201, [email protected] Dan Acheson (603) 520-4431, [email protected] Brent Drevalas (815) 687-6902, [email protected] Website: www.mlbfallball.com Twitter: @MLBazFallLeague Facebook: www.facebook.com/mlbfallball East Division Probable Starters Team W L Pct. GB Home Away Div. Stk L10 Thursday, October 15 Salt River Rafters 1 1 .500 -- 1-0 0-1 1-1 L1 1-1 Glendale at Scottsdale - 12:35 PM (L) Scottsdale Scorpions 1 1 .500 1.0 1-0 0-1 1-1 W1 1-1 RHP Brandon Brennan (3-4, 3.55 ERA in 2015) @ Mesa Solar Sox 0 2 .000 2.0 0-1 0-1 0-0 L2 0-2 RHP Aaron Wilkerson (11-3, 3.10 ERA in 2015) Salt River at Peoria - 12:35 PM (F) West Division RHP Mickey Jannis (2-3, 3.55 ERA in 2015) @ Team W L Pct. GB Home Away Div. Stk L10 RHP Jason Garcia (1-0, 4.25 ERA in ‘15 MLB) Glendale Desert Dogs 2 0 1.000 -- 1-0 1-0 0-0 W2 2-0 Mesa at Surprise* - 6:35 PM (A) Peoria Javelinas 1 1 .500 1.0 1-0 0-0 1-0 L1 1-1 RHP Jacob Esch (8-8, 3.72 ERA in 2015) @ RHP Alex Reyes (5-7, 2.49 ERA in 2015) Surprise Saguaros 1 1 .500 1.0 0-0 0-1 0-1 W1 1-1 Friday, October 16 Wednesday’s Games Scottsdale at Glendale - 12:35 p.m. -

BOSTON RED SOX (17-3) at OAKLAND A’S (10-11) Sunday, April 22, 2018 • 1:05 P.M
WORLD SERIES CHAMPIONS (8): 1903, 1912, 1915, 1916, 1918, 2004, 2007, 2013 AMERICAN LEAGUE CHAMPIONS (13): 1903, 1904, 1912, 1915, 1916, 1918, 1946, 1967, 1975, 1986, 2004, 2007, 2013 AMERICAN LEAGUE EAST DIVISION CHAMPIONS (9): 1975, 1986, 1988, 1990, 1995, 2007, 2013, 2016, 2017 AMERICAN LEAGUE WILD CARD (7): 1998, 1999, 2003, 2004, 2005, 2008, 2009 @BOSTONREDSOXPR • HTTP://PRESSROOM.REDSOX.COM • @SOXNOTES BOSTON RED SOX (17-3) at OAKLAND A’S (10-11) Sunday, April 22, 2018 • 1:05 p.m. PT/4:05 p.m. ET • Oakland Coliseum • Oakland, CA LHP David Price (2-1, 2.25) vs. RHP Daniel Mengden (2-2, 4.50) Game #21 • Road Game #12 • TV: NESN • Radio: WEEI 93.7 FM, WCEC 1490 AM/103.7 FM (Spanish) TIP YOUR CAP: Sean Manaea threw a no-hitter against the APRIL SHOWERS: The Sox are 15-2 (.882) in April, with 8 Red Sox last night, becoming the 1st pitcher to accomplish games remaining in the month...BOS has never won more REGULAR SEASON BREAKDOWN the feat vs. BOS since SEA’s Chris Bosio did so 25 years ago than 18 games in April, doing so in 1998, 2003, and 2013... AL East Standing ...........................1st, +4.0 Home/Road ..................................... 8-1/9-2 on 4/22/93 at the Kingdome. The Sox’ highest win % in any April is .846 (11-2 in 1918). Day/Night ...................................... 6-1/11-2 Prior to last night, the Sox had played 3,987 March/April ................................... 2-1/15-2 consecutive games without being no-hit, the 2nd- BAY AREA VS.