DOCSLIB.ORG

University of Florida Thesis Or Dissertation Formatting

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
University of Florida Thesis Or Dissertation Formatting DYNAMICS AND MAGNETIZATION DYNAMICS OF MAGNETIC NANOPARTICLES IN APPLIED MAGNETIC FIELDS By ZHIYUAN ZHAO A DISSERTATION PRESENTED TO THE GRADUATE SCHOOL OF THE UNIVERSITY OF FLORIDA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY UNIVERSITY OF FLORIDA 2019 © 2019 Zhiyuan Zhao To my parents Wenzhong Zhao and Mei Zhu ACKNOWLEDGMENTS At first, I would like to express my deepest gratitude to my adviser Dr. Carlos Rinaldi for giving me this opportunity to pursue doctoral studies and guiding me on the research scopes and skills. I will also appreciate for his advice and encouragement during my doctoral study, for his teaching in Continuum Basis class that has a great influence on my life, and for his help on my professional presenting and writing skills. I would like to thank Dr. David P. Arnold, Dr. Jason Butler and Dr. Ranga Narayanan, for their guidance, suggestions and support on my doctoral research and dissertation writing. I would like to give a special thank to Dr. Isaac Torres-Díaz for his patient guidance and help on my learning of coding and computational simulations. The impressive and encouraging talks with him not only contributed to my research, but also motivated me to do better in both work and life. I would like to thank Camilo Velez Cuervo and Nicolas Garraud for their hard work and contributions to my research. I would like to thank all the members in the research group, for their helps and supports in my daily life. I would like to thank my parents for supporting me to pursue my dream, and for their understanding and encourage when I got frustrated. I would like to thank the Department of Chemical Engineering for giving me the opportunity to study in the University of Florida. The advanced research facilities and inspiring academic atmosphere provided me with higher perspectives and pave me way towards further study. 4 TABLE OF CONTENTS page ACKNOWLEDGMENTS ...................................................................................................... 4 LIST OF TABLES ................................................................................................................ 7 LIST OF FIGURES .............................................................................................................. 8 LIST OF ABBREVIATIONS ............................................................................................... 11 ABSTRACT ........................................................................................................................ 12 CHAPTER 1 SCOPE OF THE DISSERTATION ............................................................................. 14 2 BROWNIAN DYNAMICS SIMULATIONS OF MAGNETIC NANOPARTICLES CAPTURED IN STRONG MAGNETIC FIELD GRADIENTS .................................... 18 2.1 Background and Motivation .................................................................................. 18 2.2 Simulation Method ................................................................................................ 22 2.2.1 Model of Magnetic Dipole for Different Relaxation Mechanisms ............... 22 2.2.2 Motion Equation .......................................................................................... 25 2.2.3 Methods to Identify and Quantify Magnetically Captured Nanoparticles .. 32 2.2.4 Simulation Parameters and Conditions ...................................................... 33 2.3 Results .................................................................................................................. 34 2.3.1 Particle Motion ............................................................................................ 34 2.3.2 Magnetic Capture Rates for Different Relaxation Mechanisms ................ 35 2.3.3 Magnetic Capture Rates for Various Strengths of The External Magnetic Field Gradient.................................................................................... 36 2.3.4 Magnetic Capture Rates for Various Nanoparticle Volume Fractions ....... 37 2.3.5 Shape of Magnetic Nanoparticle Aggregates ............................................ 38 2.4 Conclusions .......................................................................................................... 39 3 MAGNETIZATION DYNAMICS AND ENERGY DISSIPATION OF INTERACTING MAGNETIC NANOPARTICLES IN ALTERNATING MAGNETIC FIELDS WITH AND WITHOUT A STATIC BIAS FIELD ............................................ 47 3.1 Background and Motivation .................................................................................. 48 3.2 Simulation Method ................................................................................................ 51 3.2.1 Brownian Dynamics Simulations ................................................................ 51 3.2.2 Simulation Parameters and Conditions ...................................................... 52 3.2.3 Simulations of Magnetorelaxometry ........................................................... 53 3.2.4 Simulations of Dynamic Magnetic Susceptibility ........................................ 55 3.2.5 Calculation of Energy Dissipation Rate ...................................................... 56 5 3.3 Results .................................................................................................................. 56 3.3.1 Equilibrium Response of Magnetization ..................................................... 56 3.3.2 Simulations of Magnetorelaxometry ........................................................... 57 3.3.3 Energy Dissipation Rate in An Alternating Magnetic Field ........................ 60 3.3.4 Effect of Static Bias Magnetic Field on Energy Dissipation Rate .............. 63 3.4 Conclusions .......................................................................................................... 64 4 EFFECTS OF PARTICLE DIAMETER AND MAGNETOCRYSTALLINE ANISOTROPY ON MAGNETIC RELAXATOIN AND MAGNETIC PARTICLE IMAGING PERFORMACE OF MAGNETIC NANOPARTICLES ............................... 79 4.1 Background and Motivation .................................................................................. 80 4.2 Simulation Method ................................................................................................ 85 4.2.1 The Landau-Lifshitz-Gilbert (LLG) Equation .............................................. 85 4.2.2 Simulation Parameters and Conditions ...................................................... 88 4.2.3 Simulations of Magnetorelaxometry ........................................................... 89 4.2.4 Simulation Parameters and Conditions ...................................................... 91 4.3 Results .................................................................................................................. 93 4.3.1 Equilibrium Response of Magnetization ..................................................... 93 4.3.2 Simulations of Magnetorelaxometry ........................................................... 94 4.3.3 Magnetization Signal in An Alternating Magnetic Field ............................. 99 4.4 Conclusions ........................................................................................................102 5 CONCLUSION REMARKS .......................................................................................118 LIST OF REFERENCES .................................................................................................123 BIOGRAPHICAL SKETCH ..............................................................................................133 6 LIST OF TABLES Table page 3-1 Diameters used in simulations (퐷p) and corresponding diameters (퐷p,fit) obtained by applying a nonlinear fit to the Langevin function. .............................. 67 3-2 Magnetic relaxation time (휏̃) for the case that an applied static magnetic field is suddenly turned on and off for various Langevin parameters and strengths of inter-particle interactions. ................................................................................... 69 4-1 Scaled anisotropy energy ∆퐸ani⁄푘B푇 for a representative anisotropy constant value of 퐾 = 13.5 kJ⁄m3 and various nanoparticle diameters. ...........................104 7 LIST OF FIGURES Figure page 2-1 Magnetic field gradients in simulations. ................................................................. 41 2-2 Zoomed-in 3D configurations snapshots close to the capture line at various times for magnetic nanoparticles that relax by different mechanisms. ................. 42 2-3 Trajectories of representative magnetic nanoparticles that respond to the applied magnetic field by different mechanisms.................................................... 43 2-4 Number of captured magnetic nanoparticles as a function of capture time for magnetic nanoparticles that relax by the Brownian and Néel relaxation mechanisms............................................................................................................ 43 2-5 Number of captured magnetic nanoparticles as a function of capture time for various maximum Langevin parameters and magnetic nanoparticles that relax by different mechanisms. .............................................................................. 44 2-6 Number percentage of captured magnetic nanoparticles as a function of capture time for various particle volume fractions and magnetic nanoparticles that relax by different mechanisms. ....................................................................... 45 2-7 Average height and width of magnetic nanoparticle aggregates as a function of capture
Load more

Recommended publications
  • An Advanced Path Tracing Architecture for Movie Rendering
    RenderMan: An Advanced Path Tracing Architecture for Movie Rendering PER CHRISTENSEN, JULIAN FONG, JONATHAN SHADE, WAYNE WOOTEN, BRENDEN SCHUBERT, ANDREW KENSLER, STEPHEN FRIEDMAN, CHARLIE KILPATRICK, CLIFF RAMSHAW, MARC BAN- NISTER, BRENTON RAYNER, JONATHAN BROUILLAT, and MAX LIANI, Pixar Animation Studios Fig. 1. Path-traced images rendered with RenderMan: Dory and Hank from Finding Dory (© 2016 Disney•Pixar). McQueen’s crash in Cars 3 (© 2017 Disney•Pixar). Shere Khan from Disney’s The Jungle Book (© 2016 Disney). A destroyer and the Death Star from Lucasfilm’s Rogue One: A Star Wars Story (© & ™ 2016 Lucasfilm Ltd. All rights reserved. Used under authorization.) Pixar’s RenderMan renderer is used to render all of Pixar’s films, and by many 1 INTRODUCTION film studios to render visual effects for live-action movies. RenderMan started Pixar’s movies and short films are all rendered with RenderMan. as a scanline renderer based on the Reyes algorithm, and was extended over The first computer-generated (CG) animated feature film, Toy Story, the years with ray tracing and several global illumination algorithms. was rendered with an early version of RenderMan in 1995. The most This paper describes the modern version of RenderMan, a new architec- ture for an extensible and programmable path tracer with many features recent Pixar movies – Finding Dory, Cars 3, and Coco – were rendered that are essential to handle the fiercely complex scenes in movie production. using RenderMan’s modern path tracing architecture. The two left Users can write their own materials using a bxdf interface, and their own images in Figure 1 show high-quality rendering of two challenging light transport algorithms using an integrator interface – or they can use the CG movie scenes with many bounces of specular reflections and materials and light transport algorithms provided with RenderMan.
    [Show full text]
  • Sony Pictures Imageworks Arnold
    Sony Pictures Imageworks Arnold CHRISTOPHER KULLA, Sony Pictures Imageworks ALEJANDRO CONTY, Sony Pictures Imageworks CLIFFORD STEIN, Sony Pictures Imageworks LARRY GRITZ, Sony Pictures Imageworks Fig. 1. Sony Imageworks has been using path tracing in production for over a decade: (a) Monster House (©2006 Columbia Pictures Industries, Inc. All rights reserved); (b) Men in Black III (©2012 Columbia Pictures Industries, Inc. All Rights Reserved.) (c) Smurfs: The Lost Village (©2017 Columbia Pictures Industries, Inc. and Sony Pictures Animation Inc. All rights reserved.) Sony Imageworks’ implementation of the Arnold renderer is a fork of the and robustness of path tracing indicated to the studio there was commercial product of the same name, which has evolved independently potential to revisit the basic architecture of a production renderer since around 2009. This paper focuses on the design choices that are unique which had not evolved much since the seminal Reyes paper [Cook to this version and have tailored the renderer to the specic requirements of et al. 1987]. lm rendering at our studio. We detail our approach to subdivision surface After an initial period of co-development with Solid Angle, we tessellation, hair rendering, sampling and variance reduction techniques, decided to pursue the evolution of the Arnold renderer indepen- as well as a description of our open source texturing and shading language components. We also discuss some ideas we once implemented but have dently from the commercially available product. This motivation since discarded to highlight the evolution of the software over the years. is twofold. The rst is simply pragmatic: software development in service of lm production must be responsive to tight deadlines CCS Concepts: • Computing methodologies → Ray tracing; (less the lm release date than internal deadlines determined by General Terms: Graphics, Systems, Rendering the production schedule).
    [Show full text]
  • Production Global Illumination
    CIS 497 Senior Capstone Design Project Project Proposal Specification Instructors: Norman I. Badler and Aline Normoyle Production Global Illumination Yining Karl Li Advisor: Norman Badler and Aline Normoyle University of Pennsylvania ABSTRACT For my project, I propose building a production quality global illumination renderer supporting a variety of com- plex features. Such features may include some or all of the following: texturing, subsurface scattering, displacement mapping, deformational motion blur, memory instancing, diffraction, atmospheric scattering, sun&sky, and more. In order to build this renderer, I propose beginning with my existing massively parallel CUDA-based pathtracing core and then exploring methods to accelerate pathtracing, such as GPU-based stackless KD-tree construction, and multiple importance sampling. I also propose investigating and possible implementing alternate GI algorithms that can build on top of pathtracing, such as progressive photon mapping and multiresolution radiosity caching. The final goal of this project is to finish with a renderer capable of rendering out highly complex scenes and anima- tions from programs such as Maya, with high quality global illumination, in a timespan measuring in minutes ra- ther than hours. Project Blog: http://yiningkarlli.blogspot.com While competing with powerhouse commercial renderers 1. INTRODUCTION like Arnold, Renderman, and Vray is beyond the scope of this project, hopefully the end result will still be feature- Global illumination, or GI, is one of the oldest rendering rich and fast enough for use as a production academic ren- problems in computer graphics. In the past two decades, a derer suitable for usecases similar to those of Cornell's variety of both biased and unbaised solutions to the GI Mitsuba render, or PBRT.
    [Show full text]
  • On Dean W. Arnold's Writing . . . UNKNOWN EMPIRE Th E True Story of Mysterious Ethiopia and the Future Ark of Civilization “
    On Dean W. Arnold’s writing . UNKNOWN EMPIRE T e True Story of Mysterious Ethiopia and the Future Ark of Civilization “I read it in three nights . .” “T is is an unusual and captivating book dealing with three major aspects of Ethiopian history and the country’s ancient religion. Dean W. Arnold’s scholarly and most enjoyable book sets about the task with great vigour. T e elegant lightness of the writing makes the reader want to know more about the country that is also known as ‘the cradle of humanity.’ T is is an oeuvre that will enrich our under- standing of one of Africa’s most formidable civilisations.” —Prince Asfa-Wossen Asserate, PhD Magdalene College, Cambridge, and Univ. of Frankfurt Great Nephew of Emperor Haile Selassie Imperial House of Ethiopia OLD MONEY, NEW SOUTH T e Spirit of Chattanooga “. chronicles the fascinating and little-known history of a unique place and tells the story of many of the great families that have shaped it. It was a story well worth telling, and one well worth reading.” —Jon Meacham, Editor, Newsweek Author, Pulitzer Prize winner . THE CHEROKEE PRINCES Mixed Marriages and Murders — Te True Unknown Story Behind the Trail of Tears “A page-turner.” —Gordon Wetmore, Chairman Portrait Society of America “Dean Arnold has a unique way of capturing the essence of an issue and communicating it through his clear but compelling style of writing.” —Bob Corker, United States Senator, 2006-2018 Former Chairman, Senate Foreign Relations Committee THE WIZARD AND THE LION (Screenplay on the friendship between J.
    [Show full text]
  • Nvidia Rtx™ Server for Bare Metal Rendering with Autodesk Arnold 5.3.0.0 on @Xi 4029Gp- Trt2 Design Guide
    NVIDIA RTX™ SERVER FOR BARE METAL RENDERING WITH AUTODESK ARNOLD 5.3.0.0 ON @XI 4029GP- TRT2 DESIGN GUIDE VERSION: 1.0 TABLE OF CONTENTS Chapter 1. SOLUTION OVERVIEW ....................................................................... 1 1.1 NVIDIA RTX Server Overview ........................................................................... 1 Chapter 2. SOLUTION DETAILS .......................................................................... 2 2.1 Solution Configuration .................................................................................. 3 | ii Chapter 1. SOLUTION OVERVIEW Designed and tested through multi-vendor cooperation between NVIDIA and its system and ISV partners, NVIDIA RTX™ Server provides a trusted environment for artists and designers to create professional, photorealistic images for the Media & Entertainment; Architecture, Engineering & Construction; and Manufacturing & Design industries. 1.1 NVIDIA RTX SERVER OVERVIEW Introduction: Content production is undergoing a massive surge as render complexity and quality increases. Designers and artists across industries continually strive to produce more visually rich content faster than ever before, yet find their creativity and productivity bound by inefficient CPU- based render solutions. NVIDIA RTX Server is a validated solution that brings GPU-accelerated power and performance to deliver the most efficient end-to-end rendering solution, from interactive sessions in the desktop to final batch rendering in the data center. Audience: The audience for this document
    [Show full text]
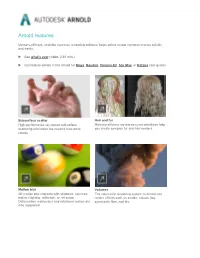
  • Arnold Features
    Arnold features Memory-efficient, scalable raytracer rendering software helps artists render complex scenes quickly and easily. See what's new (video: 2:31 min.) Get feature details in the Arnold for Maya, Houdini, Cinema 4D, 3ds Max, or Katana user guides Subsurface scatter Hair and fur High-performance ray-traced subsurface Memory-efficient ray-traced curve primitives help scattering eliminates the need to tune point you create complex fur and hair renders. clouds. Motion blur Volumes 3D motion blur interacts with shadows, volumes, The volumetric rendering system in Arnold can indirect lighting, reflection, or refraction. render effects such as smoke, clouds, fog, Deformation motion blur and rotational motion are pyroclastic flow, and fire. also supported. Instances Subdivision and displacement Arnold can more efficiently ray trace instances of Arnold supports Catmull-Clark subdivision many scene objects with transformation and surfaces. material overrides. OSL support Light Path Expressions Arnold now features support for Open Shading LPEs give you power and flexibility to create Language (OSL), an advanced shading language Arbitrary Output Variables to help meet the needs for Global Illumination renderers. of production. NEW | Adaptive sampling NEW | Toon shader Adaptive sampling gives users another means of An advanced Toon shader is part of a non- tuning images, allowing them to reduce render photorealistic solution provided in combination times without jeopardizing final image quality. with the Contour Filter. NEW | Denoising NEW | Material assignments and overrides Two denoising solutions in Arnold offer flexibility Operators make it possible to override any part of by allowing users to use much lower-quality a scene at render time and enable support for sampling settings.
    [Show full text]
  • Applying Movie-Industry Tools and Techniques to Data Visualization
    Guillermo Marin Data Analytics and Visualization Group VIRTUAL HUMANS Hyper-realistic visualisations of computer simulations BSC-SurfSara-LRZ Hyper-realistic visualisations of computer simulations Photo Scientists General public High-end visualisations of computer simulations ALYA RED ALYA RED CAMPANIAN IGNIMBRITE Scientific Reports 6, Article number: 21220 (2016) BSC Viz Team Super nice visualisations of computer simulations What we do Photo-real renders of DATA Used in short movies and still images For general public and/or peers & Why we do it Maximise impact Increase memorability BSC Viz Team Bateman, Useful junk?, 2573-2582 HOW? Film industry tools are amazing To achieve it, we need artist level Film industry people too of control over camera, light, textures, animation, and render quality Beautiful AND accurate ➡ Have scientists and artists work together ➡ Convert data from scientific software/format into animation industry standards Production pipeline Typical pipeline in animation with a few extra steps for DATA Pre-production Production Post production Script Modeling Sound & Music Data Analysis & Documentation Animation Color correction Conversion Data Casting Render Compositing Production pipeline Pre-production Production Post production Script Data Analysis & Modeling Sound & Music Documentation Conversion Animation Color correction Data Casting Inspect data in Render Compositing Sci-Viz software Data forensics if necessary Harris, S. University of Leeds Production pipeline Pre-production Production Post production Script Data
    [Show full text]
  • Introducing Arnold Single-User Questions and Answers
    Introducing Arnold Single-User Questions and Answers Overview There’s a new way to buy Arnold. Monthly, annual, and 3-year single-user subscriptions of Arnold are now available on the Autodesk e-store, simplifying the process of subscribing to, accessing, installing, and renewing Arnold. Moving the Arnold buying experience to the Autodesk e-store means you now get immediate access to your software when you subscribe, and you no longer have to install and configure multi-user license servers when you only need a single seat. Annual and 3-year single-user licenses are now also available from authorized Autodesk resellers, in addition to annual and 3-year multi-user licenses. Questions and Answers 1. What are my subscription options? There are several ways to subscribe to Arnold. If you are an individual artist or small studio rendering on a local network of workstations, your best option is to get a monthly, annual, or 3-year single-user subscription on the Autodesk e-store. Arnold will no longer be available for purchase from the Arnold website (arnoldrenderer.com). Upon subscribing to Arnold on the e-store, you will be prompted to create an Autodesk Account where you can access your subscription. If you are using Arnold on a render farm and require multi-user licenses, you can purchase annual and 3-year multi-user subscriptions from an authorized reseller. Arnold is also available for pay-per-use on the following cloud rendering platforms: AWS Thinkbox Marketplace, Microsoft Azure, Zync Render on Google Cloud Platform, and Conductor Technologies. 2. What do you mean by “single-user”? With a single-user subscription, it’s now possible to simply sign into your Autodesk account to access and start using Arnold.
    [Show full text]
  • Multimodal MRI Study of Human Brain Connectivity: Cognitive Networks
    Multimodal MRI Study of Human Brain Connectivity: Cognitive Networks Roser Sala Llonch Aquesta tesi doctoral està subjecta a la llicència Reconeixement- NoComercial – Sen seObraDerivada 3.0. Espanya de Creative Commons . Esta tesis doctoral está sujeta a la licencia Reconoc imiento - NoComercial – SinObr aDerivada 3.0. Esp aña de Creative Commons. This doctoral thesis is licensed under the Cre ative Commons Attribution- NonCommercial- NoDeriv s 3.0. Spa in License . Multimodal MRI Study of Human Brain Connectivity: Cognitive Networks Thesis presented by: Roser Sala Llonch to obtain the degree of doctor from the University of Barcelona in accordance with the requirements of the international PhD diploma Supervised by: Dr. Carme Junque´ Plaja, and Dr. David Bartres´ Faz Department of Psychiatry and Clinical Psychobiology Medicine Doctoral Program University of Barcelona 2014 A les meves `avies Barcelona, 13 November 2014 Dr. Carme Junque´ Plaja and Dr. David Bartres´ Faz, Professors at the University of Barcelona, CERTIFY that they have guided and supervised the doctoral thesis entitled ’ Multimodal MRI Study of Human Brain Connectivity: Cog- nitive Networks’ presented by Roser Sala Llonch. They hereby assert that this thesis fulfils the requirements to present her defense to be awarded the title of doctor. Signatures, Dr Carme Junque´ Plaja Dr. David Bartres´ Faz This thesis has been undertaken in the Neuropsychology Group of the Department of Psychiatry and Clinical Psychobiology, Faculty of Medicine, University of Barcelona. The group is a consolidated re- search group by the Generalitat de Catalunya ( grants 2009 SGR941 and 2014 SGR98) and it is part of the Institut d’Investigacions Biom`ediques August Pi i Sunyer (IDIBAPS).
    [Show full text]
  • TAP Animator Creed: Virtual Learning Edition
    TAP Animator Creed: Virtual Learning Edition 1 we show respect 4 we participate We are a team. We live up to the same We speak up; we ask for help when we need it. expectations as we would in person. ….. 2 we take care of our technology 5 we own the content We respect all equipment. We mute ourselves This is our class. This is our opportunity to learn when we are not speaking. We do not talk over more about the animation field. our teammates. ……………………………. 3 we focus 6 we attend class We have a lot to learn. ALL our attention is Our voices and ideas are valued. We log into focused on the class. We do our best to limit class on time and stay until the end whenever distractions around us. We wear headphones if possible. possible. Welcome to The Made In New York Animation Project NeON Summer Edition! Session 10 - Rendering Opening Share Verbally or in the Chat: What is one aspect of yourself that you want to present to the world? Technical Lesson: Rendering Terminology What is a “render”? Easy Answer Complicated Answer Whatever is on the computer screen! Whatever your 3D camera is told to look at will appear in your “render”. What are “render formats”? The Eternal Conflict: JPEG vs PNG JPEG - compressed image most PNG - a compressed Portable commonly used in articles on the web Networks Graphic image with an “Alpha layer” Alpha Layer the “blank space” in a picture that appears “clear” or transparent What is an “image sequence”? Easy Answer Complicated Answer A bunch of pictures that make a “Image sequences” are a series of movie or animation like a flipbook! renders in JPEG, PNG or other image formats that render faster and can be corrected easier than rendering a video format; ex.
    [Show full text]
  • Photorealistic Rendering for Live-Action Video Integration David E
    East Tennessee State University Digital Commons @ East Tennessee State University Undergraduate Honors Theses Student Works 5-2017 Photorealistic Rendering for LIve-Action Video Integration David E. Hirsh East Tennessee State University Follow this and additional works at: https://dc.etsu.edu/honors Part of the Interdisciplinary Arts and Media Commons Recommended Citation Hirsh, David E., "Photorealistic Rendering for LIve-Action Video Integration" (2017). Undergraduate Honors Theses. Paper 399. https://dc.etsu.edu/honors/399 This Honors Thesis - Open Access is brought to you for free and open access by the Student Works at Digital Commons @ East Tennessee State University. It has been accepted for inclusion in Undergraduate Honors Theses by an authorized administrator of Digital Commons @ East Tennessee State University. For more information, please contact [email protected]. 1 Table of Contents Abstract 3 Introduction 4 MentalRay 4 RenderMan 5 Arnold 6 Nuke Tracking and Compositing 7 Problem Solving 9 Conclusion 10 2 Abstract Exploring the creative and technical process of rendering realistic images for integration into live action footage. 3 Introduction When everything in today’s entertainment world is comprised of mostly visual effects, it only made sense to focus both my collegiate studies as well as my senior honors thesis on this field. In this paper, the reader will learn of the workflow needed to achieve realistic 3D rendering and its integration into live-action video. This paper is structured chronologically and explores my creation process and how this project has evolved, while providing image documentation from the many iterations it has undergone. MentalRay The work on this bottle initially began in 2015 for a Lighting and Rendering class my junior year.
    [Show full text]
  • Synthesis and Characterization of Metallocorrole Complexes By
    Synthesis and Characterization of Metallocorrole Complexes By Heather Louisa Buckley A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Chemistry in the Graduate Division of the University of California, Berkeley Committee in charge: Professor John Arnold, Chair Professor Kenneth Raymond Professor Ronald Gronsky Fall 2014 Synthesis and Characterization of Metallocorrole Complexes Copyright © 2014 By Heather Louisa Buckley 2 Abstract Synthesis and Characterization of Metallocorrole Complexes By Heather Louisa Buckley Doctor of Philosophy in Chemistry University of California Berkeley Professor John Arnold, Chair Chapter 1: Recent Developments in Out-of-Plane Metallocorrole Chemistry Across the Periodic Table A brief review of recent developments in metallocorrole chemistry, with a focus on species with significant displacement of the metal from the N4 plane of the corrole ring. Comparisons based on X-ray crystallographic data are made between a range of heavier transition metal, lanthanide, actinide, and main group metallocorrole species. Chapter 2: Synthesis of Lithium Corrole and its Use as a Reagent for the Preparation of Cyclopentadienyl Zirconium and Titanium Corrole Complexes The unprecedented lithium corrole complex (Mes2(p-OMePh)corrole)Li3·6THF (2- 1·6THF), prepared via deprotonation of the free-base corrole with lithium amide, acts as precursor for the preparation of cyclopentadienyl zirconium(IV) corrole (2-2) and pentamethylcyclopentadienyl titanium(IV) corrole (2-3).
    [Show full text]