Structural Diversity and the Role of Particle Shape and Dense Fluid Behavior in Assemblies of Hard Polyhedra
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Arc Length. Surface Area
Calculus 2 Lia Vas Arc Length. Surface Area. Arc Length. Suppose that y = f(x) is a continuous function with a continuous derivative on [a; b]: The arc length L of f(x) for a ≤ x ≤ b can be obtained by integrating the length element ds from a to b: The length element ds on a sufficiently small interval can be approximated by the hypotenuse of a triangle with sides dx and dy: p Thus ds2 = dx2 + dy2 ) ds = dx2 + dy2 and so s s Z b Z b q Z b dy2 Z b dy2 L = ds = dx2 + dy2 = (1 + )dx2 = (1 + )dx: a a a dx2 a dx2 2 dy2 dy 0 2 Note that dx2 = dx = (y ) : So the formula for the arc length becomes Z b q L = 1 + (y0)2 dx: a Area of a surface of revolution. Suppose that y = f(x) is a continuous function with a continuous derivative on [a; b]: To compute the surface area Sx of the surface obtained by rotating f(x) about x-axis on [a; b]; we can integrate the surface area element dS which can be approximated as the product of the circumference 2πy of the circle with radius y and the height that is given by q the arc length element ds: Since ds is 1 + (y0)2dx; the formula that computes the surface area is Z b q 0 2 Sx = 2πy 1 + (y ) dx: a If y = f(x) is rotated about y-axis on [a; b]; then dS is the product of the circumference 2πx of the circle with radius x and the height that is given by the arc length element ds: Thus, the formula that computes the surface area is Z b q 0 2 Sy = 2πx 1 + (y ) dx: a Practice Problems. -

The Continuum of Space Architecture: from Earth to Orbit
42nd International Conference on Environmental Systems AIAA 2012-3575 15 - 19 July 2012, San Diego, California The Continuum of Space Architecture: From Earth to Orbit Marc M. Cohen1 Marc M. Cohen Architect P.C. – Astrotecture™, Palo Alto, CA, 94306 Space architects and engineers alike tend to see spacecraft and space habitat design as an entirely new departure, disconnected from the Earth. However, at least for Space Architecture, there is a continuum of development since the earliest formalizations of terrestrial architecture. Moving out from 1-G, Space Architecture enables the continuum from 1-G to other gravity regimes. The history of Architecture on Earth involves finding new ways to resist Gravity with non-orthogonal structures. Space Architecture represents a new milestone in this progression, in which gravity is reduced or altogether absent from the habitable environment. I. Introduction EOMETRY is Truth2. Gravity is the constant.3 Gravity G is the constant – perhaps the only constant – in the evolution of life on Earth and the human response to the Earth’s environment.4 The Continuum of Architecture arises from geometry in building as a primary human response to gravity. It leads to the development of fundamental components of construction on Earth: Column, Wall, Floor, and Roof. According to the theoretician Abbe Laugier, the column developed from trees; the column engendered the wall, as shown in FIGURE 1 his famous illustration of “The Primitive Hut.” The column aligns with the human bipedal posture, where the spine, pelvis, and legs are the gravity- resisting structure. Caryatids are the highly literal interpretation of this phenomenon of standing to resist gravity, shown in FIGURE 2. -

Composite Concave Cupolae As Geometric and Architectural Forms
Journal for Geometry and Graphics Volume 19 (2015), No. 1, 79–91. Composite Concave Cupolae as Geometric and Architectural Forms Slobodan Mišić1, Marija Obradović1, Gordana Ðukanović2 1Faculty of Civil Engineering, University of Belgrade Bulevar kralja Aleksandra 73, 11000 Belgrade, Serbia emails: [email protected], [email protected] 2Faculty of Forestry, University of Belgrade, Serbia email: [email protected] Abstract. In this paper, the geometry of concave cupolae has been the starting point for the generation of composite polyhedral structures, usable as formative patterns for architectural purposes. Obtained by linking paper folding geometry with the geometry of polyhedra, concave cupolae are polyhedra that follow the method of generating cupolae (Johnson’s solids: J3, J4 and J5); but we removed the convexity criterion and omitted squares in the lateral surface. Instead of alter- nating triangles and squares there are now two or more paired series of equilateral triangles. The criterion of face regularity is respected, as well as the criterion of multiple axial symmetry. The distribution of the triangles is based on strictly determined and mathematically defined parameters, which allows the creation of such structures in a way that qualifies them as an autonomous group of polyhedra — concave cupolae of sorts II, IV, VI (2N). If we want to see these structures as polyhedral surfaces (not as solids) connecting the concept of the cupola (dome) in the architectural sense with the geometrical meaning of (concave) cupola, we re- move the faces of the base polygons. Thus we get a deltahedral structure — a shell made entirely from equilateral triangles, which is advantageous for the purpose of prefabrication. -

Cones, Pyramids and Spheres
The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 12 CONES, PYRAMIDS AND SPHERES A guide for teachers - Years 9–10 June 2011 YEARS 910 Cones, Pyramids and Spheres (Measurement and Geometry : Module 12) For teachers of Primary and Secondary Mathematics 510 Cover design, Layout design and Typesetting by Claire Ho The Improving Mathematics Education in Schools (TIMES) Project 2009‑2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations. The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations. © The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE‑EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution‑NonCommercial‑NoDerivs 3.0 Unported License. 2011. http://creativecommons.org/licenses/by‑nc‑nd/3.0/ The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 12 CONES, PYRAMIDS AND SPHERES A guide for teachers - Years 9–10 June 2011 Peter Brown Michael Evans David Hunt Janine McIntosh Bill Pender Jacqui Ramagge YEARS 910 {4} A guide for teachers CONES, PYRAMIDS AND SPHERES ASSUMED KNOWLEDGE • Familiarity with calculating the areas of the standard plane figures including circles. • Familiarity with calculating the volume of a prism and a cylinder. • Familiarity with calculating the surface area of a prism. • Facility with visualizing and sketching simple three‑dimensional shapes. • Facility with using Pythagoras’ theorem. • Facility with rounding numbers to a given number of decimal places or significant figures. -

Lateral and Surface Area of Right Prisms 1 Jorge Is Trying to Wrap a Present That Is in a Box Shaped As a Right Prism
CHAPTER 11 You will need Lateral and Surface • a ruler A • a calculator Area of Right Prisms c GOAL Calculate lateral area and surface area of right prisms. Learn about the Math A prism is a polyhedron (solid whose faces are polygons) whose bases are congruent and parallel. When trying to identify a right prism, ask yourself if this solid could have right prism been created by placing many congruent sheets of paper on prism that has bases aligned one above the top of each other. If so, this is a right prism. Some examples other and has lateral of right prisms are shown below. faces that are rectangles Triangular prism Rectangular prism The surface area of a right prism can be calculated using the following formula: SA 5 2B 1 hP, where B is the area of the base, h is the height of the prism, and P is the perimeter of the base. The lateral area of a figure is the area of the non-base faces lateral area only. When a prism has its bases facing up and down, the area of the non-base faces of a figure lateral area is the area of the vertical faces. (For a rectangular prism, any pair of opposite faces can be bases.) The lateral area of a right prism can be calculated by multiplying the perimeter of the base by the height of the prism. This is summarized by the formula: LA 5 hP. Copyright © 2009 by Nelson Education Ltd. Reproduction permitted for classrooms 11A Lateral and Surface Area of Right Prisms 1 Jorge is trying to wrap a present that is in a box shaped as a right prism. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Comparing Surface Area & Volume
Name ___________________________________________________________________ Period ______ Comparing Surface Area & Volume Use surface area and volume calculations to solve the following situations. 1. Find the surface area and volume of each prism. Which two have the same surface area? Which two have the same volume? 4 in. 22 in. 10 in. C A 11 in. B 18 in. 10 in. 6 in. 10 in. 6 in. 2. Sketch and label two different rectangular prisms that have the same volume. Find the surface area of each. 3. Do the following cylinders have the same surface area, the same volume, or the same surface area and volume? r = 4 cm r = 2 cm h = 9 cm h = 24 cm 4. A cylinder has a surface area of 125.6 mm2 and a volume of 100.48 mm3. If another cylinder has a radius of 5 mm and the same volume, what would be the height? 5. A cylinder has a radius of 9 yd and a height of 3 yd. A second cylinder has a radius of 6 yd and a height of 12 yd. Which statement is true? a. The cylinders have the same surface area and the same volume. b. The cylinders have the same surface area and different volumes. c. The cylinders have different surface areas and the same volume. d. The cylinders have different surface areas and different volumes. 6. The surface area of a rectangular prism is 2,116 mm2. If you double the length, width, and height of the prism, what will be the surface area of the new prism? How much larger is this amount? 7. -
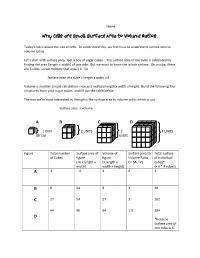
Why Cells Are Small: Surface Area to Volume Ratios
Name__________________________________ Why Cells are Small: Surface Area to Volume Ratios Today’s lab is about the size of cells. To understand this, we first have to understand surface area to volume ratios. Let’s start with surface area. Get a box of sugar cubes. The surface area of the cube is calculated by finding the area (length x width) of one side. But we want to know the whole surface. On a cube, there are 6 sides, so we multiply that area x 6. So Surface area of a cube = length x width x 6 Volume is another simple calculation – we just multiply length x width x height. Build the following four structures from your sugar cubes, and fill out the table below. The one we’re most interested in, though is the surface area to volume ratio, which is just Surface area ÷ volume A B C D 1 UNIT 2 UNITS 3 4 UNITS OR CM UNITS Figure Total number Surface area of Volume of Surface area to Total surface of Cubes figure figure Volume Ratio of individual (=6 x length x (= length x ( = SA / V) cubes* width) width x height) (= 6 * # cubes) A 1 6 1 6 1 B 8 24 8 3 48 C 27 54 27 2 162 64 96 64 1.5 384 D *because surface area of one cube is 6 Surface Area to Volume Lab Questions 1. What happened to the surface area as the size increased? It increased. 2. What happened to the volume as the size increased? It also increased, but not as quickly. -

Surface Area of 3-D Objects: Prisms: a Prism Is a Polyhedron with Two Opposite Faces That Are Identical Polygonal Regions Called the Bases
Surface Area of 3-d Objects: Prisms: A prism is a polyhedron with two opposite faces that are identical polygonal regions called the bases. The vertices of the bases are joined with segments to form the lateral faces which are parallelograms. If the lateral faces are rectangles, the prism is called a right prism, otherwise, it’s called an oblique prism. oblique right The surface area is the sum of the areas of the two bases and the areas of the lateral faces. Right rectangular prism: Right triangular prism: 5 ft 7” 4 ft 5 ft 3 ft 3” 4” 1 2 SA..243 =( )( ) + 247( )( ) + 237( )( ) SA. .=( 3)( 5) + 2 ( 3)( 4) +( 4)( 5) + ( 5) 2 bottom rectangle square top and bottom two sides two sides two triangles 2 =24 + 56 + 42 = 122in =15 + 12 + 20 + 25 = 72 ft 2 A cube has a total surface area of 384 square units. What is the length of one of its edges? The surface area of a cube is 6s2 , so 6s22= 384 s = 64 s = 8 units . If the length of the side of a cube is multiplied by 4, how will the surface area of the larger cube compare to the surface area of the original cube? 2 2 2 6s is the original surface area. 6( 4ss) = 16 6 is the new surface area, so the larger cube has 16 times the original surface area. Pyramids: A pyramid is a polyhedron formed by connecting the vertices of a polygonal region called the base to another point not in the plane of the base called the apex using segments. -

Surface Areas and Volumes
CHAPTER 13 SURFACE AREAS AND VOLUMES (A) Main Concepts and Results • Cuboid whose length = l, breadth = b and height = h (a) Volume of cuboid = lbh (b) Total surface area of cuboid = 2 ( lb + bh + hl ) (c) Lateral surface area of cuboid = 2 h (l + b) (d) Diagonal of cuboid = lbh222++ • Cube whose edge = a (a) Volume of cube = a3 (b) Lateral Surface area = 4a2 (c) Total surface area of cube = 6a2 (d) Diagonal of cube = a 3 • Cylinder whose radius = r, height = h (a) Volume of cylinder = πr2h (b) Curved surface area of cylinder = 2πrh (c) Total surface area of cylinder = 2πr (r + h) • Cone having height = h, radius = r and slant height = l 1 (a) Volume of cone = πrh2 3 (b) Curved surface area of cone = πrl 16/04/18 122 EXEMPLAR PROBLEMS (c) Total surface area of cone = πr (l + r) (d) Slant height of cone (l) = hr22+ • Sphere whose radius = r 4 (a) Volume of sphere = πr3 3 (b) Surface area of sphere = 4πr2 • Hemisphere whose radius = r 2 (a) Volume of hemisphere = πr3 3 (b) Curved surface area of hemisphere = 2πr2 (c) Total surface area of hemisphere = 3πr2 (B) Multiple Choice Questions Write the correct answer Sample Question 1 : In a cylinder, if radius is halved and height is doubled, the volume will be (A) same (B) doubled (C) halved (D) four times Solution: Answer (C) EXERCISE 13.1 Write the correct answer in each of the following : 1. The radius of a sphere is 2r, then its volume will be 4 8πr3 32 (A) πr3 (B) 4πr3 (C) (D) πr3 3 3 3 2. -

Geometrical and Static Aspects of the Cupola of Santa Maria Del Fiore, Florence (Italy)
Structural Analysis of Historic Construction – D’Ayala & Fodde (eds) © 2008 Taylor & Francis Group, London, ISBN 978-0-415-46872-5 Geometrical and static aspects of the Cupola of Santa Maria del Fiore, Florence (Italy) A. Cecchi & I. Chiaverini Department of Civil Engineering, University of Florence, Florence, Italy A. Passerini Leonardo Società di Ingegneria S.r.l., Florence, Italy ABSTRACT: The purpose of this research is to clarify, in the language of differential geometry, the geometry of the internal surface of Brunelleschi’s dome, in the Cathedral of Santa Maria del Fiore, Florence; the statics of a Brunelleschi-like dome have also been taken into consideration. The masonry, and, in particular, the “lisca pesce” one, together with the construction and layout technologies, have been main topics of interest for many researchers: they will be the subjects of further research. 1 INTRODUCTION: THE DOME OF THE CATHEDRAL OF FLORENCE The construction of the cathedral of Firenze was begun in the year 1296, with the works related to the exten- sion of the ancient church of Santa Reparata: it was designed byArnolfo (1240,1302).The design included a great dome, based on an octagonal base, to be erected in the eastern end of the church.The dome is an unusual construction of the Middle Ages, (Wittkower 1962): Arnolfo certainly referred to the nearby octagonal bap- tistery San Giovanni, so ancient and revered that the Florentines believed it was built by the Romans, as the temple of Ares, hypothesis which was not con- firmed by excavations, that set the date of foundation Figure 1. -

TECH TALK • Minnesota's Architecture
TECH TALK MINNESOTA HISTORICAL Minnesota’s Architecture • Part II SOCIETY POST-CIVIL WAR ARCHITECTURE by Charles Nelson Historical Architect, Minnesota Historical Society EDITOR’S NOTE: After a brief lull in construction during the Civil contribution to the overall aesthetic. Common materials This is the War, Minnesota witnessed a building boom in the for construction ranged from wood to brick and stone. second in a decades of the 1870s and 1880s. During these years many The Villa Style was popular from 1860 through series of five communities virtually tripled in size. Population numbers 1875. Its common characteristics include either a Tech Talk exploded and industries produced their goods around the symmetrical or an asymmetrical plan, two or three stories articles on Minnesota’s clock. The pioneer era of settlement in eastern Minnesota in height, and low-pitched hipped or gable roofs with architectural was over. Rail lines were extended to the west, and by the prominent chimneys. Ornamental treatments include styles. The end of the 1880s virtually no burgeoning town SHPO file photo next one is was without a link to another. The era of the scheduled for Greek and Gothic Revival style came to an end, the Sept. 1999 issue of only to be replaced by a more exuberant and The Interpreter. substantial architecture indicative of affluence and permanence. These expressions of progress became known as the “Bracketed Styles” and the later part of the period as the “Brownstone Era.” Figure 1, right above: the Villas Thorne-Lowell The villa as an architectural style was house in the W. introduced to the masses in Andrew Jackson 2nd St.