High-Precision Relativistic Atomic Structure Calculations and the EBIT: Tests of QED in Highly-Charged Ions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Physics 457 Particles and Cosmology Part 2 Standard Model of Particle Physics
Physics 457 Particles and Cosmology Part 2 Standard Model of Particle Physics Bing Zhou Winter 2019 Long History of Particle Physics Development 1/23/2019 Standard Model of Particle Physics The last particle in SM Higgs was discovered in 2012 A theory of matter and forces. Point-like matter particles (quarks and leptons), which interact by exchanging force carrying particles: Photons, W± and Z, gluons Particle masses are generated by Higgs Mechanism Review: Schrodinger Equation Ref. Griffiths Ch. 7 3 Review: Klein-Gordon Equation Ref. Griffiths Ch. 7 4 Review: Dirac Equation (1) Ref. Griffiths Ch. 7 γν =4x4 Dirac matrix See next page 5 Review: Dirac Equation (2) Ref. Griffiths Ch. 7 6 Review: Classical Electrodynamics In classic electrodynamics, E and B fields produced by a charge density ρ and current density j are determined by Maxwell equation. Lorentz invariant Lagrangian and eq. Field strength tensor 7 Review: EM Wave Equations (Can be derived from source less Maxwell Eqs) (no interactions) 8 The Standard Model Framework Theory is based on two principles: o Gauge invariance (well tested with experiments over 50 years) Combines Maxwell’s theory of electromagnetism, Special Relativity and Quantum field theory o Higgs Mechanism (mystery in 50 years until Higgs discovery in 2012) Massless gauge fields Massive W, Z Electroweak theory mix Massless γ Higgs field Higgs boson 9 Symmetries and Gauge Invariance Examples Symmetry Conservation Law Translation in time Energy Translation in space Momentum Rotation Angular momentum Gauge transformation Charge • Often the symmetries are built in Lagragian density function, L = T – V • Equation of motion (physics law) can be derived from Lagrangian 10 Electron Free Motion Equation Le here is an electron free (ref. -

Chapter 8 2013
described by Core Chapter 8 Electrons Wave Function e- filling spdf electronic configuration comprising (Orbital) Valence determined by Electrons described by Aufbau basis for Rules Periodic Quantum which involve Table Numbers which summarizes Orbital Pauli Hund’s which are Energy Exclusion Rule Periodic Properties Electron Configuration and Chemical Periodicity Quantum 4-quantum numbers specify the energy and location of Numbers electrons around a nucleus (all we can know). This numbers are the framework for the “electronic structure Orbital size of an atom”. Principal define & energy n = 1,2,3,.. s defines Name Symbol Permitted Values Property principal n positive integers (1,2,3...) orbital energy (size) Angular Orbital angular l orbital shape (0, 1, 2, and 3 momentum, l defines momentum integers from 0 to n-1 correspond to s, p, d, and f shape orbitals, respectively.) Magnetic Orbital magnetic integers from -l to 0 to +l orbital orientation in space defines ml ml orientation direction of e- spin spin m +1/2 or -1/2 Electron s Spin, ms defines spin Quantum Allowed Schrodinger’s equation gives an exact solution for H- Possible Orbitals Number Values atom, but does not for many electron-atoms. Electron- n Positive integers 1 2 3 electron repulsion in multi-electron split energy levels. 1,2,3,4.... Hydrogen Atom Multi-electron atoms 0 0 1 0 1 2 l 0 up to max Orbitals are of n-1 “degenerate” or Energy the same energy in Hydrogen! ml -l,...0...+l 0 0 -1 0 1 0 -1 0 1 -2-1 0 12 Orbital Name 1s 2s 2p 3s 3p 3d Electrons will Shapes or Boundry fill lowest Surface Plots energy orbitals first! Inner core electrons “shield” or “screen” outer 4-quantum numbers specify all the information we can know the energy electrons from the positive charge of the nucleus. -
![Arxiv:2101.02671V1 [Hep-Ph] 7 Jan 2021 2 Karplus and Neuman [2, 22–24], Proposals to Detect Photons Allows to Attain Εcm](https://docslib.b-cdn.net/cover/7279/arxiv-2101-02671v1-hep-ph-7-jan-2021-2-karplus-and-neuman-2-22-24-proposals-to-detect-photons-allows-to-attain-cm-807279.webp)
Arxiv:2101.02671V1 [Hep-Ph] 7 Jan 2021 2 Karplus and Neuman [2, 22–24], Proposals to Detect Photons Allows to Attain Εcm
Observing Light-by-Light Scattering in Vacuum with an Asymmetric Photon Collider Maitreyi Sangal,1 Christoph H. Keitel,1 and Matteo Tamburini1, ∗ 1Max-Planck-Institut f¨urKernphysik, Saupfercheckweg 1, D-69117 Heidelberg, Germany (Dated: January 8, 2021) Elastic scattering of two real photons is the most elusive of the fundamentally new processes predicted by quantum electrodynamics. This explains why, although first predicted more than eighty years ago, it has so far remained undetected. Here we show that in present day facilities elastic scattering of two real photons can become detectable far off axis in an asymmetric photon- photon collider setup. This may be obtained within one day operation time by colliding one millijoule XUV pulses with the broadband gamma-ray radiation generated in nonlinear Compton scattering of ultrarelativistic electron beams with terawatt-class optical laser pulses operating at 10 Hz repetition rate. In addition to the investigation of elastic photon-photon scattering, this technique allows to unveil or constrain new physics that could arise from the coupling of photons to yet undetected particles, therefore opening new avenues for searches of physics beyond the standard model. In classical electrodynamics, light beams in vacuum served directly. To date, X-ray beam experiments could pass through each other unaffected [1]. However, in only place an upper bound on the photon-photon scat- the realm of QED photons in vacuum can scatter elasti- tering cross section [41]. cally via virtual electron-positron pairs -

Ultrasoft Pseudopotentials for Lanthanide Solvation Complexes: Core Or Valence Character of the 4F Electrons Rodolphe Pollet, C
Ultrasoft pseudopotentials for lanthanide solvation complexes: Core or valence character of the 4f electrons Rodolphe Pollet, C. Clavaguéra, J.-P. Dognon To cite this version: Rodolphe Pollet, C. Clavaguéra, J.-P. Dognon. Ultrasoft pseudopotentials for lanthanide solvation complexes: Core or valence character of the 4f electrons. Journal of Chemical Physics, American Institute of Physics, 2006, 124, pp.164103 - 1-6. 10.1063/1.2191498. hal-00083928 HAL Id: hal-00083928 https://hal.archives-ouvertes.fr/hal-00083928 Submitted on 21 Jul 2006 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Ultrasoft pseudopotentials for lanthanide solvation complexes: Core or valence character of the 4f electrons Rodolphe Pollet,∗ Carine Clavagu´era, Jean-Pierre Dognon Theoretical Chemistry Laboratory DSM/DRECAM/SPAM-LFP (CEA-CNRS URA2453) CEA/SACLAY, Bat. 522, 91191 GIF SUR YVETTE, FRANCE March 6, 2006 Abstract The 4f electrons of lanthanides, because of their strong localiza- tion in the region around the nucleus, are traditionally included in a pseudopotential core. This approximation is scrutinized by optimizing 3+ the structures and calculating the interaction energies of Gd (H2O) 3+ and Gd (NH3) microsolvation complexes within plane wave PBE cal- culations using ultrasoft pseudopotentials where the 4f electrons are included either in the core or in the valence space. -

Ивй Ив Ment: #$ !% ¢&!'(&)' (( Khz Theory: #$ !% ¢&!'(&!0
Examples for precision tests of QED The effects of QED on the magnetic moment of the electron/muon and the energy levels of hydrogen, i.e. the interactions of the electron(muon) with quantum fluc- tuations of the electromagnetic field (virtual photons), have been measured with impressive precision (computed up to 5 loops): Anomalous magnetic moment: § £ ¤¦¥ ¢ ¢ ¢ ¨ ¨ © ¡ : § experiment 0.0011596521884(43) 0.001165920230(1510) theory (only QED) 0.0011596521577(230) 0.001165847057(29) theory (SM) 0.0011596521594(230) 0.001165915970(670) : taken from quantum Hall effect, : extracted from from A.Czarnecki, W.Marciano, hep-ph/0102122 ¥ Limit on electron/muon radius: fm 1S Lamb shift from measurement of transition frequencies in hydrogen: experi- ¢ ¢ ment: kHz theory: kHz ¢ " ! with proton charge radius: fm. T.van Ritbergen,K.Melnikov, hep-ph/9911277 PHY521 Elementary Particle Physics 1948: The 350 MeV Berkley synchro-cyclotron produces the first “artificial” pions: Lat- tes and Gardener observe charged pions produced by 380 MeV alpha particles by ¡ § ©¢ £¥¤ ¦ means of photographic plates ( § ). 1950: At the Berkley synchro-cyclotron Bjorkland et al. discover the neutral pion, £©¨ ¢ . 1952: Glaser invents the bubble chamber: tracks of charged particles are made visible by a trail of bubbles in superheated liquid (e.g., hydrogen). It is the necessary tool to fully exploit the newly constructed particle accelerators. The Brookhaven 3.3 GeV (reached in 1953) accelerator (Cosmotron) starts opera- tion. For the first time protons were energized to © eV at man-made accelerators. PHY521 Elementary Particle Physics The beginning of a “particle explosion” - a proliferation of hadrons: 0060.gif (GIF Image, 465x288 pixels) http://ubpheno.physics.buffalo.edu/~dow/0060.gif 1953: Reines and Cowan discover the anti-electron neutrino using a nuclear reactor as ¤ ¡ ¢ £ © anti-neutrino source ( ¢ ). -

Chapter 7 Periodic Properties of the Elements Learning Outcomes
Chapter 7 Periodic Properties of the Elements Learning Outcomes: Explain the meaning of effective nuclear charge, Zeff, and how Zeff depends on nuclear charge and electron configuration. Predict the trends in atomic radii, ionic radii, ionization energy, and electron affinity by using the periodic table. Explain how the radius of an atom changes upon losing electrons to form a cation or gaining electrons to form an anion. Write the electron configurations of ions. Explain how the ionization energy changes as we remove successive electrons, and the jump in ionization energy that occurs when the ionization corresponds to removing a core electron. Explain how irregularities in the periodic trends for electron affinity can be related to electron configuration. Explain the differences in chemical and physical properties of metals and nonmetals, including the basicity of metal oxides and the acidity of nonmetal oxides. Correlate atomic properties, such as ionization energy, with electron configuration, and explain how these relate to the chemical reactivity and physical properties of the alkali and alkaline earth metals (groups 1A and 2A). Write balanced equations for the reactions of the group 1A and 2A metals with water, oxygen, hydrogen, and the halogens. List and explain the unique characteristics of hydrogen. Correlate the atomic properties (such as ionization energy, electron configuration, and electron affinity) of group 6A, 7A, and 8A elements with their chemical reactivity and physical properties. Development of Periodic Table •Dmitri Mendeleev and Lothar Meyer (~1869) independently came to the same conclusion about how elements should be grouped in the periodic table. •Henry Moseley (1913) developed the concept of atomic numbers (the number of protons in the nucleus of an atom) 1 Predictions and the Periodic Table Mendeleev, for instance, predicted the discovery of germanium (which he called eka-silicon) as an element with an atomic weight between that of zinc and arsenic, but with chemical properties similar to those of silicon. -
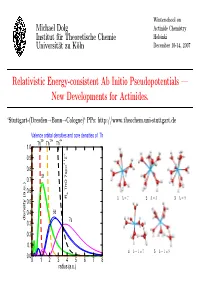
Relativistic Energy-Consistent Ab Initio Pseudopotentials — New Developments for Actinides
Winterschool on Michael Dolg Actinide Chemistry Institut fur¨ Theoretische Chemie Helsinki Universit¨at zu K¨oln December 10-14, 2007 Relativistic Energy-consistent Ab Initio Pseudopotentials — New Developments for Actinides. ‘Stuttgart-(Dresden→Bonn→Cologne)‘ PPs: http://www.theochem.uni-stuttgart.de Valence orbital densities and core densities of Th 30+ 12+ 4+ Th Th Th 1.0 + 0.9 Σ 2 1 0.8 σ 5f 0.7 0.6 ThO 7sp e R 1 h =7 2 h =8 3 h =9 0.5 0.4 6d density (a.u.) 7s 0.3 0.2 0.1 4 h − 1=7 5 h − 1=8 0.0 0 1 2 3 4 5 6 7 8 radius (a.u.) Contents • Short introduction to energy-consistent relativistic pseudopotentials • What we currently can provide for lanthanides and actinides: Wood-Boring adjusted scalar-relativistic (one-component) large-core (Ln 4f-in-core, An 5f-in-core) and small-core (Ln 4f-in-valence, An 5f-in-valence) pseudopotentials, valence spin-orbit operators in the small core case and corresponding valence basis sets of different quality (VDZ to VQZ) and contraction schemes (segmented, generalized) based on ANOs. – some general considerations concerning the choice of the core: small-core vs. large-core PPs; f-in-core PPs (superconfiguration model (R.W.Field); feudal model (B.Bursten) ?) – calibration for atoms/molecules – examples for applications • What we would like to have for lanthanides and actinides: Multi-configuration Dirac-Hartree-Fock/Dirac-Coulomb-Breit adjusted relativistic (two- and one-component) small-core pseudopotentials and corresponding correlation- consistent valence basis sets. -

High-Precision QED Calculations of the Hyperfine Structure in Hydrogen
Institut f¨ur Theoretische Physik Fakult¨at Mathematik und Naturwissenschaften Technische Universit¨at Dresden High-precision QED calculations of the hyperfine structure in hydrogen and transition rates in multicharged ions Dissertation zur Erlangung des akademischen Grades Doctor rerum naturalium vorgelegt von Andrey V. Volotka geboren am 23. September 1979 in Murmansk, Rußland Dresden 2006 Ä Eingereicht am 14.06.2006 1. Gutachter: Prof. Dr. R¨udiger Schmidt 2. Gutachter: Priv. Doz. Dr. G¨unter Plunien 3. Gutachter: Prof. Dr. Vladimir M. Shabaev Verteidigt am Contents Kurzfassung........................................ .......................................... 5 Abstract........................................... ............................................ 7 1 Introduction...................................... ............................................. 9 1.1 Theoryandexperiment . .... .... .... .... ... .... .... ........... 9 1.2 Overview ........................................ ....... 14 1.3 Notationsandconventions . ............. 15 2 Protonstructure................................... ........................................... 17 2.1 Hyperfinestructureinhydrogen . .............. 17 2.2 Zemachandmagneticradiioftheproton. ................ 20 2.3 Resultsanddiscussion . ............ 23 3 QED theory of the transition rates..................... ....................................... 27 3.1 Bound-stateQED .................................. ......... 27 3.2 Photonemissionbyanion . ........... 31 3.3 Thetransitionprobabilityinone-electronions -

QMEPC Discovery of Light's Medium Explains Why Gravity Is Larger and Weaker Odin Von Aesir* PO Box 50252, Austin, TX 78763, 925-202-6631, USA
Research & Reviews: Journal of Pure and Applied Physics QMEPC Discovery of Light's Medium Explains Why Gravity Is Larger and Weaker Odin Von Aesir* PO Box 50252, Austin, TX 78763, 925-202-6631, USA Review Article Received date: 17/11/2015 ABSTRACT Accepted date: 25/02/2016 The MEPC – The Magnetic Electron Plasma Cloud – is plasma solely Published date: 30/03/2016 composed of electrons that is the source and recipient of electrons that exist outside of the atom. The ramifications of this are nothing short of *For Correspondence phenomenal, because it not only explains where electrons come from and how they are available for distribution around the atomic nucleus, but it also Odin Von Aesir, Po Box 50252, Austin, TX explains: 78763, 925-202-6631, USA • What occupies the space in between the atoms? E-mail: [email protected] • The existence of a hierarchy of forces surrounding the atomic core, • Why gravity is larger and weaker than the other known forces, Keywords: Ramifications; Hierarchy; Proximity; • What the medium of light is, Stratosphere • Why light is both a particle and a wave, and • What dark matter and dark energy are? INTRODUCTION Furthermore, the MEPC makes logical sense of the quirkiness of quantum mechanics and the progression of time and space, because it explains the composition and connection of everything. It even gives an insight into the makeup of the atomic nucleus itself [1]. It is common knowledge that the space that surrounds us and that separates us from each other and other things here on earth is composed of air molecules that are made up of even smaller atoms. -

The Standard Model and Electron Vertex Correction
The Standard Model and Electron Vertex Correction Arunima Bhattcharya A Dissertation Submitted to Indian Institute of Technology Hyderabad In Partial Fulllment of the requirements for the Degree of Master of Science Department of Physics April, 2016 i ii iii Acknowledgement I would like to thank my guide Dr. Raghavendra Srikanth Hundi for his constant guidance and supervision as well as for providing necessary information regarding the project and also for his support in completing the project . He had always provided me with new ideas of how to proceed and helped me to obtain an innate understanding of the subject. I would also like to thank Joydev Khatua for supporting me as a project partner and for many useful discussion, and Chayan Majumdar and Supriya Senapati for their help in times of need and their guidance. iv Abstract In this thesis we have started by developing the theory for the elec- troweak Standard Model. A prerequisite for this purpose is a knowledge of gauge theory. For obtaining the Standard Model Lagrangian which de- scribes the entire electroweak SM and the theory in the form of an equa- tion, we need to develop ideas on spontaneous symmetry breaking and Higgs mechanism which will lead to the generation of masses for the gauge bosons and fermions. This is the rst part of my thesis. In the second part, we have moved on to radiative corrections which acts as a technique for the verication of QED and the Standard Model. We have started by calculat- ing the amplitude of a scattering process depicted by the Feynman diagram which led us to the calculation of g-factor for electron-scattering in a static vector potential. -

What Is XPS? X‐Ray Photoelectron Spectroscopy (XPS) Is a Surface Analytical Technique, Which Is Based Upon the Photoelectric Effect
What is XPS? X‐ray photoelectron spectroscopy (XPS) is a surface analytical technique, which is based upon the photoelectric effect. Each atom in the surface has core electron with the characteristic binding energy that is conceptually, not strictly, equal to the ionization energy of that electron. When an X‐ray beam directs to the sample surface, the energy of the X‐ray photon is adsorbed completely by the core electron of an atom. If the photon energy, h , is large enough, the core electron will then escape from the atom and emit out of the surface. The emitted electron with the kinetic energy of Ek is referred to as the photoelectron. The binding energy of the core electron is given by the Einstein relationship: Where h is the X‐ray photon energy (for monochromatic Al Ka, h = 1486.6eV);Ek is the kinetic energy of photoelectron, which can be measured by the energy analyzer; and Φ is the work function induced by the analyzer, about 4%7e5eV. Since the work function, Φ, can be compensated artificially, it is eliminated, giving the binding energy as follows: For insulating samples, once the photoelectrons are emitted out of the sample surface, a positive charge zone will establish quickly in the sample surface. As a result, the sample surface acquires a positive potential (varying typically from several volts to tens of volts) and the kinetic energies of core electrons are reduced by the same amount,C. It can be seen that the surface charging results in the shift of the XPS peaks to higher binding energy. -

Cavity Control in a Single-Electron Quantum Cyclotron: an Improved Measurement of the Electron Magnetic Moment
Cavity Control in a Single-Electron Quantum Cyclotron: An Improved Measurement of the Electron Magnetic Moment A thesis presented by David Andrew Hanneke to The Department of Physics in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the subject of Physics Harvard University Cambridge, Massachusetts December 2007 c 2007 - David Andrew Hanneke All rights reserved. Thesis advisor Author Gerald Gabrielse David Andrew Hanneke Cavity Control in a Single-Electron Quantum Cyclotron: An Improved Measurement of the Electron Magnetic Moment Abstract A single electron in a quantum cyclotron yields new measurements of the electron magnetic moment, given by g=2 = 1:001 159 652 180 73 (28) [0:28 ppt], and the fine structure constant, α−1 = 137:035 999 084 (51) [0:37 ppb], both significantly improved from prior results. The static magnetic and electric fields of a Penning trap confine the electron, and a 100 mK dilution refrigerator cools its cyclotron motion to the quantum-mechanical ground state. A quantum nondemolition measurement allows resolution of single cyclotron jumps and spin flips by coupling the cyclotron and spin energies to the frequency of the axial motion, which is self-excited and detected with a cryogenic amplifier. The trap electrodes form a high-Q microwave resonator near the cyclotron fre- quency; coupling between the cyclotron motion and cavity modes can inhibit sponta- neous emission by over 100 times the free-space rate and shift the cyclotron frequency, a systematic effect that dominated the uncertainties of previous g-value measure- ments. A cylindrical trap geometry creates cavity modes with analytically calculable couplings to cyclotron motion.