The Prediction of Shallow Landslide Location and Size Using a Multidimensional Landslide Analysis in a Digital Terrain Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Landslides on the Loess Plateau of China: a Latest Statistics Together with a Close Look
Landslides on the Loess Plateau of China: a latest statistics together with a close look Xiang-Zhou Xu, Wen-Zhao Guo, Ya- Kun Liu, Jian-Zhong Ma, Wen-Long Wang, Hong-Wu Zhang & Hang Gao Natural Hazards Journal of the International Society for the Prevention and Mitigation of Natural Hazards ISSN 0921-030X Volume 86 Number 3 Nat Hazards (2017) 86:1393-1403 DOI 10.1007/s11069-016-2738-6 1 23 Your article is protected by copyright and all rights are held exclusively by Springer Science +Business Media Dordrecht. This e-offprint is for personal use only and shall not be self- archived in electronic repositories. If you wish to self-archive your article, please use the accepted manuscript version for posting on your own website. You may further deposit the accepted manuscript version in any repository, provided it is only made publicly available 12 months after official publication or later and provided acknowledgement is given to the original source of publication and a link is inserted to the published article on Springer's website. The link must be accompanied by the following text: "The final publication is available at link.springer.com”. 1 23 Author's personal copy Nat Hazards (2017) 86:1393–1403 DOI 10.1007/s11069-016-2738-6 SHORT COMMUNICATION Landslides on the Loess Plateau of China: a latest statistics together with a close look 1,2 2 2 Xiang-Zhou Xu • Wen-Zhao Guo • Ya-Kun Liu • 1 1 3 Jian-Zhong Ma • Wen-Long Wang • Hong-Wu Zhang • Hang Gao2 Received: 16 December 2016 / Accepted: 26 December 2016 / Published online: 3 January 2017 Ó Springer Science+Business Media Dordrecht 2017 Abstract Landslide plays an important role in landscape evolution, delivers huge amounts of sediment to rivers and seriously affects the structure and function of ecosystems and society. -

A Study of Unstable Slopes in Permafrost Areas: Alaskan Case Studies Used As a Training Tool
A Study of Unstable Slopes in Permafrost Areas: Alaskan Case Studies Used as a Training Tool Item Type Report Authors Darrow, Margaret M.; Huang, Scott L.; Obermiller, Kyle Publisher Alaska University Transportation Center Download date 26/09/2021 04:55:55 Link to Item http://hdl.handle.net/11122/7546 A Study of Unstable Slopes in Permafrost Areas: Alaskan Case Studies Used as a Training Tool Final Report December 2011 Prepared by PI: Margaret M. Darrow, Ph.D. Co-PI: Scott L. Huang, Ph.D. Co-author: Kyle Obermiller Institute of Northern Engineering for Alaska University Transportation Center REPORT CONTENTS TABLE OF CONTENTS 1.0 INTRODUCTION ................................................................................................................ 1 2.0 REVIEW OF UNSTABLE SOIL SLOPES IN PERMAFROST AREAS ............................... 1 3.0 THE NELCHINA SLIDE ..................................................................................................... 2 4.0 THE RICH113 SLIDE ......................................................................................................... 5 5.0 THE CHITINA DUMP SLIDE .............................................................................................. 6 6.0 SUMMARY ......................................................................................................................... 9 7.0 REFERENCES ................................................................................................................. 10 i A STUDY OF UNSTABLE SLOPES IN PERMAFROST AREAS 1.0 INTRODUCTION -

Types of Landslides.Indd
Landslide Types and Processes andslides in the United States occur in all 50 States. The primary regions of landslide occurrence and potential are the coastal and mountainous areas of California, Oregon, Land Washington, the States comprising the intermountain west, and the mountainous and hilly regions of the Eastern United States. Alaska and Hawaii also experience all types of landslides. Landslides in the United States cause approximately $3.5 billion (year 2001 dollars) in dam- age, and kill between 25 and 50 people annually. Casualties in the United States are primar- ily caused by rockfalls, rock slides, and debris flows. Worldwide, landslides occur and cause thousands of casualties and billions in monetary losses annually. The information in this publication provides an introductory primer on understanding basic scientific facts about landslides—the different types of landslides, how they are initiated, and some basic information about how they can begin to be managed as a hazard. TYPES OF LANDSLIDES porate additional variables, such as the rate of movement and the water, air, or ice content of The term “landslide” describes a wide variety the landslide material. of processes that result in the downward and outward movement of slope-forming materials Although landslides are primarily associ- including rock, soil, artificial fill, or a com- ated with mountainous regions, they can bination of these. The materials may move also occur in areas of generally low relief. In by falling, toppling, sliding, spreading, or low-relief areas, landslides occur as cut-and- La Conchita, coastal area of southern Califor- flowing. Figure 1 shows a graphic illustration fill failures (roadway and building excava- nia. -

Landslide Triggering Mechanisms
kChapter 4 GERALD F. WIECZOREK LANDSLIDE TRIGGERING MECHANISMS 1. INTRODUCTION 2.INTENSE RAINFALL andslides can have several causes, including Storms that produce intense rainfall for periods as L geological, morphological, physical, and hu- short as several hours or have a more moderate in- man (Alexander 1992; Cruden and Vames, Chap. tensity lasting several days have triggered abun- 3 in this report, p. 70), but only one trigger (Varnes dant landslides in many regions, for example, 1978, 26). By definition a trigger is an external California (Figures 4-1, 4-2, and 4-3). Well- stimulus such as intense rainfall, earthquake shak- documented studies that have revealed a close ing, volcanic eruption, storm waves, or rapid stream relationship between rainfall intensity and acti- erosion that causes a near-immediate response in vation of landslides include those from California the form of a landslide by rapidly increasing the (Campbell 1975; Ellen et al. 1988), North stresses or by reducing the strength of slope mate- Carolina (Gryta and Bartholomew 1983; Neary rials. In some cases landslides may occur without an and Swift 1987), Virginia (Kochel 1987; Gryta apparent attributable trigger because of a variety or and Bartholomew 1989; Jacobson et al. 1989), combination of causes, such as chemical or physi- Puerto Rico (Jibson 1989; Simon et al. 1990; cal weathering of materials, that gradually bring the Larsen and Torres Sanchez 1992)., and Hawaii slope to failure. The requisite short time frame of (Wilson et al. 1992; Ellen et al. 1993). cause and effect is the critical element in the iden- These studies show that shallow landslides in tification of a landslide trigger. -

Liquefaction, Landslide and Slope Stability Analyses of Soils: a Case Study Of
Nat. Hazards Earth Syst. Sci. Discuss., doi:10.5194/nhess-2016-297, 2016 Manuscript under review for journal Nat. Hazards Earth Syst. Sci. Published: 26 October 2016 c Author(s) 2016. CC-BY 3.0 License. 1 Liquefaction, landslide and slope stability analyses of soils: A case study of 2 soils from part of Kwara, Kogi and Anambra states of Nigeria 3 Olusegun O. Ige1, Tolulope A. Oyeleke 1, Christopher Baiyegunhi2, Temitope L. Oloniniyi2 4 and Luzuko Sigabi2 5 1Department of Geology and Mineral Sciences, University of Ilorin, Private Mail Bag 1515, 6 Ilorin, Kwara State, Nigeria 7 2Department of Geology, Faculty of Science and Agriculture, University of Fort Hare, Private 8 Bag X1314, Alice, 5700, Eastern Cape Province, South Africa 9 Corresponding Email Address: [email protected] 10 11 ABSTRACT 12 Landslide is one of the most ravaging natural disaster in the world and recent occurrences in 13 Nigeria require urgent need for landslide risk assessment. A total of nine samples representing 14 three major landslide prone areas in Nigeria were studied, with a view of determining their 15 liquefaction and sliding potential. Geotechnical analysis was used to investigate the 16 liquefaction potential, while the slope conditions were deduced using SLOPE/W. The results 17 of geotechnical analysis revealed that the soils contain 6-34 % clay and 72-90 % sand. Based 18 on the unified soil classification system, the soil samples were classified as well graded with 19 group symbols of SW, SM and CL. The plot of plasticity index against liquid limit shows that 20 the soil samples from Anambra and Kogi are potentially liquefiable. -

Seismic Hazards Mapping Act Fact Sheet
Department of Conservation California Geological Survey Seismic Hazards Mapping Act Fact Sheet The Seismic Hazards Mapping Act (SHMA) of 1990 (Public Resources Code, Chapter 7.8, Section 2690-2699.6) directs the Department of Conservation, California Geological Survey to identify and map areas prone to earthquake hazards of liquefaction, earthquake-induced landslides and amplified ground shaking. The purpose of the SHMA is to reduce the threat to public safety and to minimize the loss of life and property by identifying and mitigating these seismic hazards. The SHMA was passed by the legislature following the 1989 Loma Prieta earthquake. Staff geologists in the Seismic Hazard Mapping Program (Program) gather existing geological, geophysical and geotechnical data from numerous sources to compile the Seismic Hazard Zone Maps. They integrate and interpret these data regionally in order to evaluate the severity of the seismic hazards and designate Zones of Required Investigation for areas prone to liquefaction and earthquake–induced landslides. Cities and counties are then required to use the Seismic Hazard Zone Maps in their land use planning and building permit processes. The SHMA requires site-specific geotechnical investigations be conducted identifying the seismic hazard and formulating mitigation measures prior to permitting most developments designed for human occupancy within the Zones of Required Investigation. The Seismic Hazard Zone Maps identify where a site investigation is required and the site investigation determines whether structural design or modification of the project site is necessary to ensure safer development. A copy of each approved geotechnical report including the mitigation measures is required to be submitted to the Program within 30 days of approval of the report. -

DISSERTATION LANDSLIDE RESPONSE to CLIMATE CHANGE in DENALI NATIONAL PARK, ALASKA, and OTHER PERMAFROST REGIONS Submitted By
DISSERTATION LANDSLIDE RESPONSE TO CLIMATE CHANGE IN DENALI NATIONAL PARK, ALASKA, AND OTHER PERMAFROST REGIONS Submitted by Annette Patton Department of Geosciences In partial fulfillment of the requirements For the Degree of Doctor of Philosophy Colorado State University Fort Collins, Colorado Summer 2019 Doctoral Committee: Advisor: Sara Rathburn Ellen Wohl John Singleton Jeffrey Niemann Copyright by Annette Patton 2019 All Rights Reserved ABSTRACT LANDSLIDE RESPONSE TO CLIMATE CHANGE IN DENALI NATIONAL PARK, ALASKA, AND OTHER PERMAFROST REGIONS Rapid permafrost thaw in the high-latitude and high-elevation areas increases hillslope susceptibility to landsliding by altering geotechnical properties of hillslope materials, including reduced cohesion and increased hydraulic connectivity. The overarching goal of this study is to improve the understanding of geomorphic controls on landslide initiation at high latitudes. In this dissertation, I present a literature review, surficial mapping and a landslide inventory, and site-specific landslide monitoring to evaluate landslide processes in permafrost regions. Following an introduction to landslides in permafrost regions (Chapter 1), the second chapter synthesizes the fundamental processes that will increase landslide frequency and magnitude in permafrost regions in the coming decades with observational and analytical studies that document landslide regimes in high latitudes and elevations. In Chapter 2, I synthesize the available literature to address five questions of practical importance, -

Sliding in the Farmington Siding Landslide Complex, Davis County, Utah
Hylland, Lowe LIQUEFACTION CHARACTERISTICS,CHARACTERISTICS, TIMING,TIMING, ANDAND HAZARDHAZARD POTENTIALPOTENTIAL OFOF LIQUEFACTION-INDUCEDLIQUEFACTION-INDUCED LANDSLIDINGLANDSLIDING ININ THETHE FARMINGTONFARMINGTON SIDINGSIDING LANDSLIDELANDSLIDE COMPLEX,COMPLEX, DAVISDAVIS COUNTY,COUNTY, UTAHUTAH by Michael D. Hylland and Mike Lowe - INDUCED LANDSLIDING, FARMINGTON SIDING LANDSLIDE COMPLEX, DAVIS COUNTY, UTAH UGS Special Study 95 UTAH COUNTY, SIDING LANDSLIDE COMPLEX, DAVIS INDUCED LANDSLIDING, FARMINGTON Aerial view looking northwest along Interstate 15, showing hummocky landslide terrain on northern part of Farmington Siding landslide complex. Backhoe trench excavated on a hummock sideslope within the Farmington Siding landslide complex, with the Wasatch Range Trench exposure of liquefied sand and in the background. Block of organic soil incorporated into disrupted silt interbed. landslide deposits during landsliding. SPECIAL STUDY 95 1998 UTAH GEOLOGICAL SURVEY a division of Utah Department of Natural Resources CHARACTERISTICS, TIMING, AND HAZARD POTENTIAL OF LIQUEFACTION-INDUCED LANDSLIDING IN THE FARMINGTON SIDING LANDSLIDE COMPLEX, DAVIS COUNTY, UTAH by Michael D. Hylland and Mike Lowe Research supported by the U.S. Geological Survey (USGS), Department of the Interior, under USGS award number 1434-94-G-2498. The views and conclusions contained in this document are those of the authors and should not be interpreted as necessarily representing the official policies, either expressed or implied, of the U.S. Government. SPECIAL STUDY 95 1998 UTAH GEOLOGICAL SURVEY a division of Utah Department of Natural Resources CONTENTS Abstract . 1 Introduction . 2 Previous Work . 2 Geology and Geomorphology . 3 Trench Descriptions . 4 Trench FST1 . 5 Trench FST2 . 7 Trench FST3 . 7 Trench FST4 . 7 Trench FST5 . 11 Slope-Failure Modes and Extent of Internal Deformation . -

FEMA Landslide Fact Sheet
Fact Sheet Federal Emergency Management Agency / Region X February, 2009 sheet Fact FEMA DR-1817-WA LANDS L IDES : Is your home SAFE? Landslides occur throughout Washington, most commonly during the wet If your house is in danger winter months. As the population of Washington grows, there are increasing of landslide damage, pressures to develop in landslide-prone areas, so that knowledge of these leave immediately. hazards has become increasingly important. If you live in or are planning to move into or build a new home in a landslide-prone area, here are some Don’t delay! important things to consider. S URN B Is my home in a landslide-prone area? COTT S Become familiar with the land around you, especially if you live on or near steep slopes, and learn whether landslides or debris flows have occurred in your area. Channels, streams, gullies, ponds, and erosion on slopes indicate potential prob- lems. Road and driveway drains, as well as gutters and downspouts, can con- centrate and accelerate flow. Ground saturation and concentrated, rapid surface runoff are major causes of slope failure and subsequent landslides. Fig. 1 - Landslide indicators. Vegetative characteristics can indicate slope conditions. Bare slopes may show evidence of erosion and sliding. Trees that bend downhill or tilt uphill (Fig.1) are also hints that the ground has moved. Ferns or other wet-loving plants often indicate seeps or springs that create saturated ground, which can lead to slope failure. Structural deformation such as cracks in foundations, walls and chimneys (Fig.2); gaps between floors and walls; misaligned or sticking doors and windows; fail- ing retaining walls; cracks in driveways, curbs and roads; and tilted power poles Fig. -

Landslide and Liquefaction Maps for the Long Beach Peninsula
LANDSLIDE AND LIQUEFACTION MAPS FOR THE LONG BEACH PENINSULA, PACIFIC COUNTY, WASHINGTON: Effects on Tsunami Inundation Zones of a Cascadia Subduction Zone Earthquake by Stephen L. Slaughter, Timothy J. Walsh, Anton Ypma, Kelsay M. D. Stanton, Recep Cakir, and Trevor A. Contreras WASHINGTON DIVISION OF GEOLOGY AND EARTH RESOURCES Report of Investigations 37 October 2013 DISCLAIMER Neither the State of Washington, nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the State of Washington or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the State of Washington or any agency thereof. WASHINGTON STATE DEPARTMENT OF NATURAL RESOURCES Peter Goldmark—Commissioner of Public Lands DIVISION OF GEOLOGY AND EARTH RESOURCES David K. Norman—State Geologist John P. Bromley—Assistant State Geologist Washington Department of Natural Resources Division of Geology and Earth Resources Mailing Address: Street Address: MS 47007 Natural Resources Bldg, Rm 148 Olympia, WA 98504-7007 1111 Washington St SE Olympia, WA 98501 Phone: 360-902-1450; Fax: 360-902-1785 E-mail: [email protected] Website: http://www.dnr.wa.gov/geology Publications List: http://www.dnr.wa.gov/researchscience/topics/geologypublications library/pages/pubs.aspx Online searchable catalog of the Washington Geology Library: http://www.dnr.wa.gov/researchscience/topics/geologypublications library/pages/washbib.aspx Washington State Geologic Information Portal: http://www.dnr.wa.gov/geologyportal Suggested Citation: Slaughter, S. -

Earthquake-Induced Landslides in Central America
Engineering Geology 63 (2002) 189–220 www.elsevier.com/locate/enggeo Earthquake-induced landslides in Central America Julian J. Bommer a,*, Carlos E. Rodrı´guez b,1 aDepartment of Civil and Environmental Engineering, Imperial College of Science, Technology and Medicine, Imperial College Road, London SW7 2BU, UK bFacultad de Ingenierı´a, Universidad Nacional de Colombia, Santafe´ de Bogota´, Colombia Received 30 August 2000; accepted 18 June 2001 Abstract Central America is a region of high seismic activity and the impact of destructive earthquakes is often aggravated by the triggering of landslides. Data are presented for earthquake-triggered landslides in the region and their characteristics are compared with global relationships between the area of landsliding and earthquake magnitude. We find that the areas affected by landslides are similar to other parts of the world but in certain parts of Central America, the numbers of slides are disproportionate for the size of the earthquakes. We also find that there are important differences between the characteristics of landslides in different parts of the Central American isthmus, soil falls and slides in steep slopes in volcanic soils predominate in Guatemala and El Salvador, whereas extensive translational slides in lateritic soils on large slopes are the principal hazard in Costa Rica and Panama. Methods for assessing landslide hazards, considering both rainfall and earthquakes as triggering mechanisms, developed in Costa Rica appear not to be suitable for direct application in the northern countries of the isthmus, for which modified approaches are required. D 2002 Elsevier Science B.V. All rights reserved. Keywords: Landslides; Earthquakes; Central America; Landslide hazard assessment; Volcanic soils 1. -
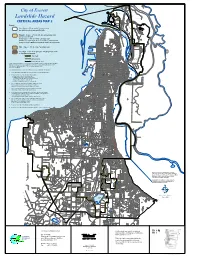
Landslide Hazard E L R a (P E RI N H VA G TE) W E A
ST EA M B O A T S L ) O 9 9 U Y G W H H D L O ( 9 2 5 - R (PR S U IVAT E) 36 N TH P City of Everett L NE IO 5 N E T A S T L S R O E T N U I W G E H SPENCER ISLAND Y SMITH ISLAND E L R E N A (P RIVAT H E G E) W. S V MITH A IS A LA O ND R Landslide Hazard U OAD H O T S 5 N E 3 R D N 2 3 ) E E 28TH P T L N NE A V G I OLF C E O RD R V CRITICAL AREAS MAP 2 P A E ( T J A E V O N I VATE) 27TH PL NE R RI E (P P H V A N H T S S 5 3 M O I Legend: T N H S LOUGH S D L N O A L U Low Slopes < 25% in “other” geologic units S I G Y W E H T S T T M E A R R O (not Qtb, Qw, Qls or uncontrolled fill). J I S N S E A 2ND ST V V IE E W D R R D E W M IE A R V 3RD ST S B IN S E R M N E N I ID V I R O T R G I A E H D E W M H W D Qtb, Qw, Qls geologic units E A I W R O 4TH ST Y S N Medium Slopes < 15% for I L M L A Y N D K I V S D L S B MEDORA H N AY O 5TH ST W and uncontrolled fill S 5 WHITE R R TH ST E HORSE V I N IL L TRA V R A O D E E 6TH ST T E E K .