A Complex Networks Approach to Ranking Professional Snooker Players
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

ORDER of PLAY Wednesday 13 November 2019
19.com Northern Ireland Open 2019 ORDER OF PLAY Wednesday 13 November 2019 START TIME: 10:00 Table Match # Player 1 Result Player 2 Referee/Marker Maike Kesseler TABLE 1 92 Barry Hawkins Michael Holt Leo Scullion TABLE 2 72 Liang Wenbo Tian Pengfei Nico De Vos TABLE 3 69 Yan Bingtao Marco Fu Luise Kraatz TABLE 4 67 Si Jiahui Chen Zifan Alex Crisan TABLE 5 71 Jak Jones Anthony Hamilton Rob Spencer TABLE 6 70 Rod Lawler Andrew Higginson Terry Camilleri TABLE 7 83 Robbie Williams Hammad Miah Malgorzata Kanieska TABLE 8 86 Martin O'Donnell Alexander Ursenbacher Monika Sulkowska START TIME: 13:00 Not before 13:00 Table Match # Player 1 Result Player 2 Referee/Marker 75 Matthew Selt Luca Brecel Glen Sullivan-Bisset 76 Soheil Vahedi Ken Doherty John Pellew 77 Thepchaiya Un-Nooh Mei Xiwen Greg Coniglio 78 Mitchell Mann Harvey Chandler Proletina Velichkova 80 Chen Feilong Billy Castle REFEREE TBC 88 Ian Burns Scott Donaldson REFEREE TBC Kevin Dabrowski TABLE 1 74 Mark Selby Matthew Stevens Plamena Manolova TABLE 2 68 Ali Carter Li Hang Colin Humphries START TIME: 14:00 Roll-on Roll-off Table Match # Player 1 Result Player 2 Referee/Marker 79 Mark Davis Stephen Maguire REFEREE TBC 84 Joe Perry Ross Bulman REFEREE TBC TABLE 1 66 Judd Trump Zhang Anda REFEREE TBC TABLE 2 73 Peter Ebdon Kyren Wilson REFEREE TBC START TIME: 16:30 Table Match # Player 1 Result Player 2 Referee/Marker TABLE 1 87 Jordan Brown Stuart Bingham REFEREE TBC TABLE 2 82 Mark Joyce Jackson Page REFEREE TBC Powered by Sportradar | http://www.sportradar.com | Tuesday, Nov 12 2019 23:45:30 | © World Snooker. -
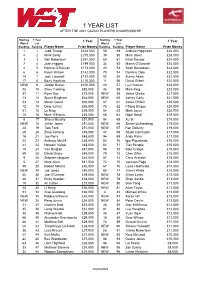
Master Money List After 2021 Players Champs.Xlsx
1 YEAR LIST AFTER THE 2021 CAZOO PLAYERS CHAMPIONSHIP Starting 1 Year 1 YearStarting 1 Year 1 Year World List World List Ranking Ranking Player Name Prize MoneyRanking Ranking Player Name Prize Money 1 1 Judd Trump £454,500 59 49 Andrew Higginson £24,000 4 2 Mark Selby £270,500 39 50 Mark Davis £24,000 3 3 Neil Robertson £261,000 60 51 Elliot Slessor £24,000 7 4 John Higgins £199,500 34 52 Martin O'Donnell £24,000 2 5 Ronnie O'Sullivan £173,500 23 53 Scott Donaldson £23,000 6 6 Kyren Wilson £142,000 70 54 Dominic Dale £22,500 14 7 Jack Lisowski £132,000 52 55 Sunny Akani £22,500 17 8 Barry Hawkins £110,500 11 56 David Gilbert £22,500 NEW 9 Jordan Brown £100,000 43 57 Lyu Haotian £22,000 25 10 Zhou Yuelong £83,500 36 58 Mark King £22,000 37 11 Ryan Day £73,000 NEW 59 Jamie Clarke £21,500 13 12 Stuart Bingham £68,000 NEW 60 Ashley Carty £21,000 53 13 Martin Gould £66,000 87 61 Jamie O'Neill £20,500 12 14 Ding Junhui £65,500 78 62 Chang Bingyu £20,000 51 15 Lu Ning £59,500 64 63 Mark Joyce £20,000 10 16 Mark Williams £53,500 68 64 Nigel Bond £19,500 8 17 Shaun Murphy £51,500 84 65 Xu Si £19,000 NEW 18 Jamie Jones £51,000 NEW 66 Simon Lichtenberg £19,000 24 19 Tom Ford £51,000 NEW 67 Ken Doherty £19,000 29 20 Zhao Xintong £49,500 47 68 Stuart Carrington £17,500 16 21 Joe Perry £48,500 94 69 Andy Hicks £17,000 22 22 Anthony McGill £48,000 82 70 Igor Figueiredo £16,000 41 23 Hossein Vafaei £48,000 54 71 Tian Pengfei £15,500 15 24 Yan Bingtao £47,500 58 72 Sam Craigie £15,500 69 25 David Grace £45,000 79 73 Chen Zifan £15,000 9 26 Stephen Maguire -

BBC Sport Snooker ITT 2021-24
ITT – Snooker 2021-24 INVITATION TO TENDER Host TV production and domestic live BBC TV/Red Button/BBC iPlayer coverage of the: ➢ UK Championship ➢ UK Masters ➢ World Snooker Championship Starting with the UK Championship in 2021, ending with the World Championship in 2024 . ITT – Snooker 2021-24 Contents SECTION A: INTRODUCTION PAGE 2 SECTION B: REQUIREMENTS PAGE 7 SECTION C: INSTRUCTIONS TO TENDERERS PAGE 13 SECTION D: KEY CONTRACT TERMS PAGE 17 SECTION E: NON-DISCLOSURE AGREEMENT PAGE 19 SECTION F: FORM OF TENDER PAGE 24 SECTION G: REGIONAL CRITERIA PAGE 26 ITT – Snooker 2021-24 Section A – Introduction S e c t i o n A – Introduction 1 BACKGROUND 1.1 The BBC provides a diverse range of broadcast services under a Royal Charter. The greater portion of the BBC’s income comes from the licence fee. In spending this money, the BBC has an obligation to demonstrably secure best value for money for the licence fee payer in all aspects of its day-to-day activities. 1.2 The BBC is unique in British broadcasting. Its reputation is built on quality, public service, distinctiveness, objectivity and indigenous programme making. 1.3 Recent years have seen fundamental changes in the broadcasting industry, with more competition and a wider range of services. The BBC now offers numerous TV channels, an online presence, major radio networks and over 40 local radio stations, as well as a range of other services. 1.4 A key part of demonstrating value for money in delivering the BBC’s services is the continuing need to form effective and strategic supplier relationships. -

Sangsom 6 Red World Championship 5 September 2016
SangSom 6 Red World Championship 5 September 2016 TIME M # GRP T PLAYER 1 - COUNTRYVS PLAYER 2 - COUNTRY score M1 H1-H5 1 Mark Selby ENG 5 : 3 Moh Keen Hoo MAS 55:8,0:49,34:25,0:43,45:1,6:48,69(69):0,38:26 M2 H2-H4 2 Matthew Selt ENG 5 : 2 Peter McCullagh AUS 69(61):0,55:0,13:43,38:8,0:42,54:1,42:4 M3 H3-H6 3 Luca Brecel BEL 5 : 3 Boonyarit Kaettikul THA 29:34,11:48,54:9,38:5,43:37,11:47,41:20,64:0 M4 B1-B5 4 Martin Gould ENG 5 : 0 Basem Eltahhan EGY 38:17,49:0,61(61):1,46:29,55:1 11:00 M5 B2-B4 5 Liang Wenbo CHN 5 : 0 Chau Hon Man HKG 73(73):0,47:4,72(67):0,57(57):0,52:17 a.m. M6 B3-B6 6 Michael Holt ENG 4 : 5 Akani Songsermsawad THA 47:0,0:42,0:52,56:0,54:1,29:21,23:49,13:40,0:71(67) M7 C1-C5 7 Ding Junhui CHN 4 : 5 Pankaj Advani IND 0:46,42:10,0:46,40:0,12:40,66:0,47:0,16:50,0:38 M8 C2-C4 8 Robert Milkins ENG 5 : 4 Ryan Thomerson AUS 16:49,1:42,3:45,38:0,43:0,41:0,0:36,36:31,40:8 M9 C3-C6 9 Dominic Dale WAL 3 : 5 Phaitoon Phonbun THA 8:46,38:41,0:50,40:0,60:23,48:4,1:65(65),14:35 M10 G3-G4 10 Mateusz Baranowski POL 5 : 1 Daniell Haenga NZL 41:8,1:57,51:35,36:21,32:20,25:22 TIME M # GRP T PLAYER 1 - COUNTRYVS PLAYER 2 - COUNTRY score M11 D1-D6 1 Ricky Walden ENG 5 : 1 Kritsanut Lertsattayatorn THA 24:34,36:0,56:6,32:21,31:12,35:6 M12 D2-D3 2 David Gilbert ENG 5 : 2 Ben Woollaston ENG 56:0,66:0,30:40,29:36,44:6,51:1,43:41 M13 D4-D5 3 Andrew Pagett WAL 3 : 5 Ahmed Galal EGY 29:34,15:43,28:20,24:34,30:44,43:3,48:0,14:31 M14 F1-F5 4 Joe Perry ENG 5 : 4 Hesham Abdelaziz EGY 0:53,29:32,45:20,11:33,66(66):0,28:19,18:37,39:0,38:1 1:30 M15 F2-F4 5 Michael White WAL 5 : 3 Sourav Kothari IND 16:30,50:10,56:8,70(70):4,39:1,0:46,3:36,36:27 p.m. -

ORDER of PLAY Thursday 16 February 2017
Coral Welsh Open ORDER OF PLAY Thursday 16 February 2017 START TIME: 12:00 Table Match # Player 1 Result Player 2 Referee/Marker Rob Spencer TABLE 1 103 Thepchaiya Un-Nooh Barry Hawkins Peter Williamson TABLE 2 100 Graeme Dott Lee Walker Luise Kraatz TABLE 3 107 Dominic Dale Igor Figueiredo Terry Camilleri TABLE 4 97 Mark Davis Fergal O'Brien Malgorzata Kanieska TABLE 5 104 Anthony Hamilton Craig Steadman Tatiana Woollaston TABLE 6 99 Zhou Yuelong Ross Muir Glen Sullivan-Bisset TABLE 7 98 Jimmy Robertson Scott Donaldson Jan Scheers TABLE 8 108 Stuart Carrington Robin Hull Haydn Parry START TIME: 13:00 Table Match # Player 1 Result Player 2 Referee/Marker Colin Humphries TABLE 1 101 Judd Trump Jackson Page Peter Williamson TABLE 2 105 Stuart Bingham Ian Burns Nigel Leddie TABLE 3 106 Michael White Robbie Williams Martyn Royce TABLE 4 110 Mark Allen Mei Xiwen John Pellew TABLE 5 102 Allister Carter Hossein Vafaei Ayouri Alex Crisan TABLE 6 109 Josh Boileau Robert Milkins Joery Ector START TIME: 14:30 Table Match # Player 1 Result Player 2 Referee/Marker TABLE 1 112 Yan Bingtao Mark Selby REFEREE TBC TABLE 2 111 Kurt Maflin Mitchell Mann REFEREE TBC START TIME: 19:00 Table Match # Player 1 Result Player 2 Referee/Marker 113 WINNER OF MATCH 97 WINNER OF MATCH 98 REFEREE TBC 114 WINNER OF MATCH 99 WINNER OF MATCH 100 REFEREE TBC 116 WINNER OF MATCH 103 WINNER OF MATCH 104 REFEREE TBC 118 WINNER OF MATCH 107 WINNER OF MATCH 108 REFEREE TBC START TIME: 20:00 Table Match # Player 1 Result Player 2 Referee/Marker 115 WINNER OF MATCH 101 WINNER OF MATCH 102 REFEREE TBC 117 WINNER OF MATCH 105 WINNER OF MATCH 106 REFEREE TBC 119 WINNER OF MATCH 109 WINNER OF MATCH 110 REFEREE TBC 120 WINNER OF MATCH 111 WINNER OF MATCH 112 REFEREE TBC Powered by Sportradar | http://www.sportradar.com | Wednesday, Feb 15 2017 23:52:40 | © World Snooker.. -

Prize Money Rankings After German Masters 2018
WORLD RANKINGS AFTER THE 2018 D88 GERMAN MASTERS Start Current Prize Money Ranking Ranking Player Name Rankings 1 1 Mark Selby 1,419,025 14 2 Ronnie O'Sullivan 722,750 3 3 Judd Trump 704,250 4 4 Ding Junhui 653,425 2 5 John Higgins 537,550 8 6 Shaun Murphy 516,400 16 7 Mark Williams 430,750 6 8 Barry Hawkins 402,725 10 9 Mark Allen 400,450 5 10 Marco Fu 373,650 9 11 Stuart Bingham 328,087 12 12 Ali Carter 328,025 7 13 Neil Robertson 322,625 13 14 Kyren Wilson 314,250 27 15 Luca Brecel 309,650 17 16 Anthony McGill 283,800 19 17 Ryan Day 281,137 11 18 Liang Wenbo 262,650 24 19 Stephen Maguire 259,925 20 20 Mark King 237,950 22 21 Joe Perry 228,850 21 22 Ricky Walden 227,975 15 23 Martin Gould 195,050 18 24 David Gilbert 183,700 30 25 Graeme Dott 180,425 23 26 Michael Holt 175,575 56 27 Yan Bingtao 167,625 26 28 Michael White 162,525 39 29 Xiao Guodong 158,925 25 30 Anthony Hamilton 157,925 29 31 Alan McManus 150,400 31 32 Zhou Yuelong 148,075 28 33 Ben Woollaston 146,275 38 34 Jimmy Robertson 144,512 34 35 Robert Milkins 143,775 33 36 Tom Ford 141,600 58 37 Li Hang 134,950 54 38 Jack Lisowski 131,662 32 39 Dominic Dale 125,050 48 40 Mark Joyce 124,437 36 41 Mark Davis 116,125 52 42 Kurt Maflin 112,762 37 43 Matthew Selt 108,900 43 44 Mike Dunn 108,450 59 45 Hossein Vafaei 107,100 47 46 Yu DeLu 104,225 40 47 Peter Ebdon 103,987 35 48 Jamie Jones 102,987 05/02/2018 WORLD RANKINGS AFTER THE 2018 D88 GERMAN MASTERS Start Current Prize Money Ranking Ranking Player Name Rankings 45 49 Fergal O'Brien 101,987 57 50 Gary Wilson 97,987 42 51 Thepchaiya -

World Rankings After the 2016 Paul Hunter Classic
WORLD RANKINGS AFTER THE 2016 PAUL HUNTER CLASSIC Start Current Prize Money Ranking Ranking Player Name Rankings 1 1 Mark Selby 675,150 2 2 Stuart Bingham 582,034 3 3 Shaun Murphy 455,308 5 4 Judd Trump 401,166 6 5 John Higgins 400,725 7 6 Mark Allen 363,592 4 7 Neil Robertson 359,582 8 8 Ricky Walden 312,208 9 9 Ding Junhui 311,425 11 10 Joe Perry 295,133 10 11 Ronnie O'Sullivan 294,333 13 12 Mark Williams 251,008 12 13 Marco Fu 243,750 16 14 Kyren Wilson 226,924 32 15 Allister Carter 214,200 14 16 Barry Hawkins 213,525 15 17 Martin Gould 196,559 28 18 Anthony McGill 193,125 17 19 Liang Wenbo 179,584 18 20 Stephen Maguire 179,250 19 21 Michael White 175,258 22 22 David Gilbert 166,792 25 23 Matthew Selt 155,300 23 24 Ryan Day 153,357 20 25 Alan McManus 152,934 24 26 Graeme Dott 151,933 21 27 Robert Milkins 147,366 29 28 Michael Holt 145,683 27 29 Ben Woollaston 137,599 26 30 Mark Davis 136,791 30 31 Luca Brecel 128,299 31 32 Peter Ebdon 126,842 33 33 Thepchaiya Un-Nooh 126,541 34 34 Jimmy Robertson 106,650 36 35 Mark King 99,984 38 36 Dominic Dale 91,642 37 37 Mike Dunn 90,958 43 38 Tom Ford 90,558 35 39 Jamie Jones 90,283 42 40 Gary Wilson 86,141 40 41 Fergal O'Brien 79,333 44 42 Matthew Stevens 78,766 39 43 Jack Lisowski 78,016 50 44 Kurt Maflin 76,600 45 45 Dechawat Poomjaeng 76,424 46 46 Sam Baird 73,274 47 47 Rod Lawler 72,624 48 48 Tian Pengfei 72,133 31/08/2016 WORLD RANKINGS AFTER THE 2016 PAUL HUNTER CLASSIC Start Current Prize Money Ranking Ranking Player Name Rankings 54 49 Zhou Yuelong 71,925 41 50 Mark Joyce 71,383 52 51 -

Two Kuwaiti Women Infected with Coronavirus Variant: Moh
JAMADA ALTHANI 7, 1442 AH WEDNESDAY, JANUARY 20, 2021 16 Pages Max 23º Min 08º 150 Fils Established 1961 ISSUE NO: 18339 The First Daily in the Arabian Gulf www.kuwaittimes.net Trump spends last day in White Pandemic reveals hidden Oldest city in the Americas ‘Miracle’ at the Gabba 5 House, Biden goes to Washington 9 poverty in wealthy Japan 13 under threat from squatters 16 as India stun Australia Two Kuwaiti women infected with coronavirus variant: MoH Kuwait reports 578 new cases, 2 deaths • Sharp drop in hospital, ICU occupancy By Nawara Fattahova positive after PCR tests were conducted upon arrival ago, authorities launched a vaccination campaign tions to 1,415,197. Sanad said the latest statistics on at Kuwait airport. using Pfizer-BioNTech vaccines. bed occupancy at public hospitals and health institu- KUWAIT: Two Kuwaiti women who arrived from Additional genetic tests carried out found the two The ministry of health yesterday announced 578 tions show a drop in COVID-19 cases treated in hos- Britain have tested positive for a new COVID-19 women had contracted the new strain of the coron- new COVID-19 cases in the last 24 hours, raising the pitals as well as a drop in cases in intensive care strain, the first discovery of the more contagious avirus, Sanad said. The ministry of health immediately total caseload to 158,822. Sanad also announced two units. “During a certain period last year, occupancy coronavirus variant found in the United Kingdom and took all necessary measures including isolating the deaths in the same period, taking the death toll to of COVID-19 wards in hospitals reached above 50 several other countries, the health ministry two patients and placing them in quarantine. -

Al-Neel, Pereira Shine in Markhiya's Win Over Shamal
NNBABA | Page 5 TTENNISENNIS | Page 6 Harden hits Sharapova heights as falls to Garcia in Rockets soar Stuttgart over Wolves fi rst round Wednesday, April 25, 2018 FOOTBALL Sha’baan 9, 1439 AH Unstoppable GULF TIMES Ronaldo the sole survivor of ‘BBC’ SPORT Page 3 FOCUS Impressive medal haul for Qatar at Arab athletics By Sports Reporter (Shot Put and Discus) in the recent On the last day of competition, Doha GCC Championship held in Kuwait, Rashid al-Suwaidi added a bronze student athlete Mohamed Ibrahim medal for his exploits in long jump and Moaaz maintained his fabulous form Team Qatar picked up their last medal, spire Academy student ath- to repeat the feat in the same events a bronze, thanks to the blistering pace letes led Qatar’s charge for in Amman. of Jaber Hilal al-Mamari in the 200m medals at the 18th Arab It was a similar tale with rising star sprint. Junior Athletics Champion- athlete, Muhand Saifeldin, who like Team Qatar’s athletes were among Aships held from April 19-22, 2018, at Mooaz, matched his two gold medal 423 competing at the 18th Arab Junior the Baccalaureate School in Amman, haul from the GCC Championship but Athletics Championships that featured Jordan. this time round also added a 800m win athletes from 16 countries across 44 The team brought home a total of in place of the 1,500m he won in Ku- events. seven medals on the back of some im- wait. His fi rst gold came in the 3,000m pressive performances that ensured steeplechase. -

1 Stephen Hendry
aus: Hugo Kastner: SNOOKER – Spieler, Regeln & Rekorde Update: März 2010 Ergänzung: Programmheft Stephen Hendry MBE – „Der Größte“ Geboren: 13. Januar 1969 in Edinburgh, Schottland Professional: seit 1985 High Break: 147 (8-mal) Höchstes Ranking: No.1 (1990/91, 1991/92, 1992/93, 1993/94, 1994/95, 1995/96, 1996/97, 1997/98, 2006/07) – Rekord Siege Ranking Turniere: 36 World Champion: 7-mal (1990, 1992, 1993, 1994, 1995, 1996, 1999) – Rekord Stephen Hendry gehört zu den Sportlern, die neben phänomenalem Talent auch unglaubliche Willensstärke und Kaltblütigkeit mitbringen. Gerade unter Druck läuft er zu Höchstform auf, nie gibt er sich mit guten 40 oder 50 Punkten zufrieden, sondern sieht fast nur im Abräumen des Tisches die wahre Perfektion. Seit seinem ersten Auftauchen als Professional hat Stephen Hendry praktisch alle Rekorde gebrochen, die es im modernen Snooker zu brechen gibt. Siebenmal wurde er World Champion, zudem als jüngster Spieler, dem dies im Crucible Theatre je gelang, achtmal konnte er ein Maximum auf den Tisch zaubern, mehr als 700 Century Breaks stehen in seiner Statistik zu Buche, und er führt auch überlegen die Liste der Rankingturniersieger an. Hendry schaffte 2002 sensationelle 16 Centuries in einem Turnier, er machte 1997 gegen Jimmy White als bis dahin einziger Spieler der Geschichte ein Maximum in einem Entscheidungssatz, und er war seit Einführung des neuen Ranglistensystems unerreichte achtmal in Serie die Nummer 1 der Welt. Kein Wunder, dass im goldenen Jahrzehnt des Schotten die Gegner schon eingeschüchtert waren, wenn Stephen auch nur den Turniersaal betrat. Dabei kam Hendry erst relativ spät zu diesem Sport. Zwei Wochen vor seinem 13. -

Sporting Legends: Stephen Hendry
SPORTING LEGENDS: STEPHEN HENDRY SPORT: SNOOKER COMPETITIVE ERA: 1984 - PRESENT Stephen Hendry MBE (born January 13, 1969, Auchterarder, Perthshire, Scotland) is a Scottish professional snooker player. Hendry has won the World Snooker Championships seven times, a record for the modern era, and is thus regarded by many as the greatest player of all time. Hendry started his career early. He was Scottish Amateur Champion at the age of 15, and turned professional aged just 16. Hendry first won the World Professional Snooker Championship in 1990 at the age of 21, becoming the youngest player ever to win the event. He went on to dominate the game in the 1990s. His most recent win in 1999 was his seventh, eclipsing rival Steve Davis's six modern era victories. Hendry holds several snooker records: He has earned more prize money than any other player (about £7 million); he has scored the most 147s (eight times), and is the only player to have scored a 147 in a major final, a feat he has achieved three times. He has compiled the most century breaks, currently over 660, and he holds the most ranking event titles (34). In 1990/1991, despite not winning the World Championships, he won an amazing five ranking events, a record for a single season. Hendry was ranked number 1 from 1990 to 1998 in a record breaking 8 season streak. Hendry was awarded an MBE in 1994 and voted BBC Scotland's Sports Personality of the Year in 1987 and 1996. SPORTING LEGENDS: STEPHEN HENDRY Stephen Hendry is a true snooker legend. -

Snooker Superstar
Snooker Superstar 1 Snooker Superstar 台球巨星 Star Profile – Ding Junhui 新星简介--丁俊辉 Read the text below and do the activity that follows. 阅读下面的短文,然后完成练习: If 2005 was the year that Ding Junhui exploded onto the international snooker scene, then 2006 could be the year he becomes a legend. Ding fulfilled his potential in a nail-biting confrontation with Steve Davis in the final of the prestigious UK Championship last December. He defeated the six-time world champion by 10 frames to 6 in a thrilling final at the Barbican Centre in York. In defeating Davis he has already secured a place in history as he is the first ever player from outside the British Isles to win the UK Championship. Having won his first prize in competitive snooker at the age of thirteen, Ding is unquestionably a precocious talent. It seems that he has now matured into a world-class player – “It was only a matter of time before he joined the world’s elite”, says Steve Davis. Ding’s talent has been developed by his father, Ding Wenjun who became aware of his son’s remarkable abilities when he was just eight years old. Ding Wenjun explains, “When I was playing with my friends, he was attracted by the colourful balls and would play by himself on another table for a whole day”. Many years of hard work and sacrifice followed as Ding’s father gave up his business and moved to Dongguan in order to find better training facilities for his son. Both father and son lived in cramped conditions, sharing a five- square-metre room adjoining the local snooker club.