Macroeconomic Potentials of Transatlantic Free Trade 1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Prof. Gabriel Felbermayr, Ph.D
CV G. Felbermayr (Jan. 2021) Prof. Gabriel Felbermayr, Ph.D. President of the Kiel Institute for the World Economy Kiel Institute for the World Economy Presidential Department Kiellinie 66 24105 Kiel, Germany Phone: +49 431 8814-236 Email: [email protected] Website: www.ifw-kiel.de/felbermayr Main research themes • International trade theory and policy: World Trade Organization, trade conflicts, preferential trade agreements; gravity modelling, structurally estimated GE models • Labor economics: Trade and labor market outcomes, search-and-matching models, international migration • Environmental economics: Trade and CO2-emissions • European Union economics: Brexit, integration models • Business cycle analysis Selected Current Professional Affiliations Since March 2019 President of the Kiel Institute for the World Economy Since March 2019 Professor of Economics and Economic Policy, Faculty of Economics, University of Kiel Member, Scientific Advisory Board, German Federal Ministry of Economics and Energy Elected Member of the Executive Council, Verein für Socialpolitik Chairman, Advisory Board, EcoAustria Institut für Wirtschaftsforschung Member, Advisory Committee “Econonmic Symposium”, European Forum Alpbach Member, Scientific Advisory Board, Stiftung Familienunternehmen Member, Scientific Advisory Board, Afrika-Verein der deutschen Wirtschaft Member, McKinsey Germany Advisory Group Member, Expert Group “Global economy and social ethics”, Konferenz Weltkirche Member, Advisory Board, Herbert Giersch Stiftung CESifo Research Network -

Program Overview „Global Solutions“ Summit 2019 Overarching Theme: Recoupling Social and Economic Progress — Towards a New International Paradigm
Program Overview „Global Solutions“ Summit 2019 Overarching Theme: Recoupling Social and Economic Progress — Towards a New International Paradigm March 17, 2019 Venue: Berlin City Hall / Rotes Rathaus (Rathausstraße 15, 10178 Berlin) 18:00 Welcome Reception Speeches • Michael Müller (Governing Mayor of Berlin, Germany) • Dennis Snower (President, Global Solutions Initiative (GSI)) • Dennis Görlich (Research Coordinator, Global Solutions Initiative (GSI); Head of Global Challenges Center, Kiel Institute for the World Economy (IfW)) March 18, 2019 Venue: ESMT Berlin (Schloßplatz 1, 10178 Berlin) 08:30 – 9:20 Welcome Main Stage II • Jörg Rocholl (President, ESMT Berlin) • Michael Müller (Governing Mayor of Berlin, Germany) • Dennis Snower (President, Global Solutions Initiative (GSI)) 09:20-09:40 Opening Address: Toward Global Paradigm Change Main Stage II • Dennis Snower (President, Global Solutions Initiative (GSI)) 09:45 – 10:45 Opening Plenary: Toward Global Paradigm Change Main Stage II • Ronnie C. Chan (Chairman, Hang Lung Properties) • Colm Kelly (Global Leader - Tax and Legal Services and Global Leader - Purpose, PwC) • Gabriela Ramos (Chief of Staff and Sherpa to the G20, OECD) • Dennis Snower (President, Global Solutions Initiative (GSI)) • Ngaire Woods (Founding Dean of Blavatnik School of Government, Oxford University) • Naoyuki Yoshino (Dean and CEO, Asian Development Bank Institute (ADBI)) Moderator: Evan Davis (Journalist and Presenter, BBC) 11:00 – 12:50 Saving the WTO Parallel Session -------------------------- _________________ -

FIW-Forschungskonferenz 2008
Save the Date 12th FIW-Research Conference ‘International Economics’ 5-6 December 2019 WIFO Austrian Institute of Economic Research Arsenal, Object 20 1030 Vienna Scientific Board FIW: Harald Oberhofer, Robert Stehrer and WU Vienna: Harald Badinger Fritz Breuss University of Ljubljana: Jože P. Damijan University of Vienna: Alejandro Cunat Universita di Bologna: Gaetano A. Minerva IOS Regensburg: Olga Popova University of Economics Bratislava: Mikulas IfW Kiel: Gabriel Felbermayr Luptacik MTA KRTK: Márta Bisztray FIW is a cooperation of FIW is supported by We thank the FIW partner institutions for their cooperation in the organisation of this conference: 12th FIW Research Conference ‘International Economics’ Programme Outline Date: December 5-6 2019(Thursday from 10:00 a.m. to 7.00 p.pm and Friday from 9.00 a.m. to 1.00 p.m.) Venue: WIFO, Austrian Institute of Economic Research Arsenal, Object 20, 1030 Vienna Conference Programme Outline: The Research Centre International Economics - FIW invites to its 12th Research Conference ‘International Economics’. The main objective of the conference is to provide a platform for economists working in the field of ‘International Economics’ in Austria and its neighbouring countries to present recent research as well as to discuss current policy. Recent working papers from both young researchers – i.e. Ph.D. students, post- graduate students, young faculty members etc. – and established senior researchers will be presented during parallel sessions focusing on one topic of ‘International Economics’. -

Undoing Europe in a New Quantitative Trade Model
250 ifo 2018 WORKING January 2018 PAPERS Undoing Europe in a New Quantitative Trade Model Gabriel Felbermayr, Jasmin Gröschl, Inga Heiland Impressum: ifo Working Papers Publisher and distributor: ifo Institute – Leibniz Institute for Economic Research at the University of Munich Poschingerstr. 5, 81679 Munich, Germany Telephone +49(0)89 9224 0, Telefax +49(0)89 985369, email [email protected] www.cesifo-group.de An electronic version of the paper may be downloaded from the ifo website: www.cesifo-group.de ifo Working Paper No. 250 Undoing Europe in a New Quantitative Trade Model* Abstract We employ theory-grounded sectoral gravity models to estimate the effects of various steps of European product market integration on trade flows. We embed these estimates into a static Ricardian quantitative trade model featuring 43 countries and 50 goods and services sectors. Paying attention to the role of non-tariff trade barriers and of intra- and international value added networks, we simulate lower bounds to the trade, output, and welfare effects of different disintegration scenarios. Bootstrapping standard errors, we find statistically significant welfare losses of up to 23% of the 2014 baseline, but we also document a strong degree of heterogeneity across EU insiders. Effects on EU outsiders are often insignificant. The welfare effects from the Single Market dominate quantitatively, but the gains from Schengen and Eurozone membership are substantial for many countries as well. Percentage losses are more pronounced for more central EU members, while larger and richer countries tend to lose less. The effects of income transfers reveal some surprising patterns driven by terms-of-trade adjustments. -

Cesifo Working Paper No. 9079
9079 2021 May 2021 Decoupling Global Value Chains Peter Eppinger, Gabriel Felbermayr, Oliver Krebs, Bohdan Kukharskyy Impressum: CESifo Working Papers ISSN 2364-1428 (electronic version) Publisher and distributor: Munich Society for the Promotion of Economic Research - CESifo GmbH The international platform of Ludwigs-Maximilians University’s Center for Economic Studies and the ifo Institute Poschingerstr. 5, 81679 Munich, Germany Telephone +49 (0)89 2180-2740, Telefax +49 (0)89 2180-17845, email [email protected] Editor: Clemens Fuest https://www.cesifo.org/en/wp An electronic version of the paper may be downloaded · from the SSRN website: www.SSRN.com · from the RePEc website: www.RePEc.org · from the CESifo website: https://www.cesifo.org/en/wp CESifo Working Paper No. 9079 Decoupling Global Value Chains Abstract Recent disruptions to global value chains (GVCs) have raised an important question: Can decoupling from GVCs increase a country’s welfare by reducing its exposure to foreign supply shocks? We use a quantitative trade model to simulate GVCs decoupling, defined as increased barriers to global input trade. After decoupling, the repercussions of foreign supply shocks are reduced on average, but some countries experience magnified effects. Across various scenarios, welfare losses from decoupling far exceed any benefits from lower shock exposure. In the U.S., a repatriation of GVCs would reduce national welfare by 2.2% but barely change U.S. exposure to foreign shocks. JEL-Codes: F110, F120, F140, F170, F620. Keywords: quantitative -

CURRICULUM VITAE Prof. Dr. Lisandra Flach
CURRICULUM VITAE Prof. Dr. Lisandra Flach Office address Personal data ifo Center for International Economics Citizenship: Brazilian, German Poschingerstr. 5, 81679 Munich, Germany. Place of birth: Florian´opolis, Brazil +(49)(0)89 9224 1428 Date of birth: January 28, 1983 Email: [email protected] Married, one daughter Home page: https://sites.google.com/site/lisandraflach CURRENT EMPLOYMENT AND AFFILIATIONS Professor of Economics, esp. Economics of Globalisation, LMU Munich Director, ifo Center for International Economics Research Affiliate, CEPR, since 2016 Research Affiliate, CESifo, since 2015 Committee for International Economics, German Economic Association (VfS), since 2019 Research Fellow, SFB CRC TRR 190, German Research Foundation, since 2017 Editoral Board, International Economics, since 2017 EDUCATION 2007-2012 University of Mannheim, PhD in Economics (Dr. rer. pol., summa cum laude). CDSE - Center for Doctoral Studies in Economics. 2010 University of California, San Diego. Affiliate Graduate Student. 2001-2006 UFSC - Federal University of Santa Catarina, Brazil. Economics Degree, 4.5-year degree. Prize for the highest final GPA. 2001-2006 UDESC/ESAG - Santa Catarina State University, Brazil. Business Administration Degree, 5-year degree. PREVIOUS ACADEMIC APPOINTMENTS AND RESEARCH VISITS 2012-2020 LMU Munich Assistant Professor, Department of Economics. 01-02/2018 University of California, San Diego Visiting Researcher, Economics Department. 28.11-12/2016 Harvard University Visiting Researcher, Economics Department. 09-10/2015 Columbia University Visiting Scholar, Economics Department. Summer-Fall 2012 Ifo Institute and German Ministry of Economics and Technology Consultant. Project on Multilateral Trade Agreements. 2012-2013 OECD Consultant at the Economics Department. Summer-Fall 2010 University of California, San Diego Research Assistant to Prof. -

Trade and Unemployment: What Do the Data Say?
IZA DP No. 4184 Trade and Unemployment: What Do the Data Say? Gabriel Felbermayr Julien Prat Hans-Jörg Schmerer May 2009 DISCUSSION PAPER SERIES Forschungsinstitut zur Zukunft der Arbeit Institute for the Study of Labor Trade and Unemployment: What Do the Data Say? Gabriel Felbermayr University of Stuttgart-Hohenheim Julien Prat University of Vienna, New York University and IZA Hans-Jörg Schmerer University of Tübingen and University of Stuttgart-Hohenheim Discussion Paper No. 4184 May 2009 IZA P.O. Box 7240 53072 Bonn Germany Phone: +49-228-3894-0 Fax: +49-228-3894-180 E-mail: [email protected] Any opinions expressed here are those of the author(s) and not those of IZA. Research published in this series may include views on policy, but the institute itself takes no institutional policy positions. The Institute for the Study of Labor (IZA) in Bonn is a local and virtual international research center and a place of communication between science, politics and business. IZA is an independent nonprofit organization supported by Deutsche Post Foundation. The center is associated with the University of Bonn and offers a stimulating research environment through its international network, workshops and conferences, data service, project support, research visits and doctoral program. IZA engages in (i) original and internationally competitive research in all fields of labor economics, (ii) development of policy concepts, and (iii) dissemination of research results and concepts to the interested public. IZA Discussion Papers often represent preliminary work and are circulated to encourage discussion. Citation of such a paper should account for its provisional character. A revised version may be available directly from the author. -

Program Overview „Global Solutions“ Summit 2019 Overarching Theme: Recoupling Social and Economic Progress — Towards a New International Paradigm
Program Overview „Global Solutions“ Summit 2019 Overarching Theme: Recoupling Social and Economic Progress — Towards a New International Paradigm March 17, 2019 Venue: Berlin City Hall / Rotes Rathaus (Rathausstraße 15, 10178 Berlin) 19:00 – 22:00 Welcome Reception Speeches Michael Müller (Governing Mayor of Berlin, Germany) Dennis Snower (President, Global Solutions Initiative (GSI)) Dennis Görlich (Head of Global Challenges Center, Kiel Institute for the World Economy (IfW)) March 18, 2019 Venue: ESMT Berlin (Schloßplatz 1, 10178 Berlin) 09:00 – 9:45 Welcome Addresses Main Stage II Jörg Rocholl (President, ESMT Berlin) Michael Müller (Governing Mayor of Berlin, Germany) Dennis Snower (President, Global Solutions Initiative (GSI)) Moderator: Penelope Winterhager (Head of Resort “Politics and Concepts”, Tagesspiegel Berlin) 10:00 – 10:50 Opening Plenary: Paradigm Change Main Stage II Ronnie Chan* (Chairman ,Hang Lung Group Limited) Colm Kelly (Leader, Global Tax and Legal Services; former Vice Chairman, PwC) Gabriela Ramos (Chief of Staff and Sherpa to the G20, OECD) Dennis Snower (President, Global Solutions Initiative (GSI)) Ngaire Woods (Founding Dean of Blavatnik School of Government, Oxford University) Naoyuki Yoshino (Dean and CEO, Asian Development Bank Institute (ADBI)) Moderator: Evan Davis (Journalist and Presenter, BBC) 11:00 – 12:50 Saving the WTO Parallel Session ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐ _________________ Kiel Institute for the World Main Stage II Economy Panel Chad Bown (Senior Fellow, Peterson Institute for -

12Th FIW Research Conference Programme
12th FIW-Research Conference ‘International Economics’ 5-6 December 2019 WIFO Austrian Institute of Economic Research Arsenal, Object 20 1030 Vienna Scientific Board FIW: Harald Oberhofer, Robert Stehrer and Fritz Breuss University of Vienna: Alejandro Cunat IOS Regensburg: Olga Popova IfW Kiel: Gabriel Felbermayr MTA KRTK: Márta Bisztray WU Vienna: Harald Badinger University of Ljubljana: Jože P. Damijan Universita di Bologna: Gaetano A. Minerva University of Economics Bratislava: Mikulas Luptacik FIW is a cooperation of FIW is supported by We thank the FIW partner institutions for their cooperation in the organisation of this conference: 12th FIW Research Conference ‘International Economics’ Programme Outline Date: December 5-6 2019 (Thursday from 10:00 to 19:00 and Friday from 9:00 to 13:00) Venue: WIFO, Austrian Institute of Economic Research Arsenal, Object 20, 1030 Vienna Conference Programme Outline: The Research Centre International Economics - FIW invites to its 12th Research Conference ‘International Economics’. The main objective of the conference is to provide a platform for economists working in the field of ‘International Economics’ in Austria and its neighbouring countries to present recent research as well as to discuss current policy. Recent working papers from both young researchers – i.e. Ph.D. students, post-graduate students, young faculty members etc. – and established senior researchers will be presented during parallel sessions focusing on one topic of ‘International Economics’. Highlights: • 5 December 2019, 10:00: -
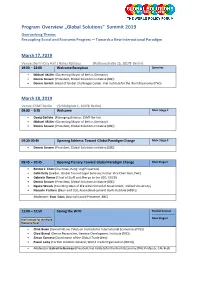
Program Overview „Global Solutions“ Summit 2019 Overarching Theme: Recoupling Social and Economic Progress — Towards a New International Paradigm
Program Overview „Global Solutions“ Summit 2019 Overarching Theme: Recoupling Social and Economic Progress — Towards a New International Paradigm March 17, 2019 Venue: Berlin City Hall / Rotes Rathaus (Rathausstraße 15, 10178 Berlin) 19:00 – 22:00 Welcome Reception Speeches • Michael Müller (Governing Mayor of Berlin, Germany) • Dennis Snower (President, Global Solutions Initiative (GSI)) • Dennis Görlich (Head of Global Challenges Center, Kiel Institute for the World Economy (IfW)) March 18, 2019 Venue: ESMT Berlin (Schloßplatz 1, 10178 Berlin) 09:00 – 9:20 Welcome Main Stage II • Georg Garlichs (Managing Director, ESMT Berlin) • Michael Müller (Governing Mayor of Berlin, Germany) • Dennis Snower (President, Global Solutions Initiative (GSI)) 09:20-09:40 Opening Address: Toward Global Paradigm Change Main Stage II • Dennis Snower (President, Global Solutions Initiative (GSI)) 09:45 – 10:45 Opening Plenary: Toward Global Paradigm Change Main Stage II • Ronnie C. Chan (Chairman, Hang Lung Properties) • Colm Kelly (Leader, Global Tax and Legal Services; former Vice Chairman, PwC) • Gabriela Ramos (Chief of Staff and Sherpa to the G20, OECD) • Dennis Snower (President, Global Solutions Initiative (GSI)) • Ngaire Woods (Founding Dean of Blavatnik School of Government, Oxford University) • Naoyuki Yoshino (Dean and CEO, Asian Development Bank Institute (ADBI)) Moderator: Evan Davis (Journalist and Presenter, BBC) 11:00 – 12:50 Saving the WTO Parallel Session _________________ -------------------------- Main Stage II Kiel Institute for the -

Curriculum Vitae
JULIEN PRAT CREST Phone: +33 (0)1 41 17 60 81 15 Boulevard Gabriel Peri Email: [email protected] 92245 Malakoff Cedex, France Web: http://prat.iae-csic.org Personal Details Date of Birth September 9, 1974 Citizenship French Language Skills French; English; Italian; Spanish; German Academic Positions 2012-present Research Scientist (CNRS), CREST, Paris, France 2009-present Tenured Scientist, Institute for Economic Analysis, CSIC, Barcelona, Spain 2008-2009 Visiting Scholar, New York University, Department of Economics, USA 2004-2008 Assistant Professor, University of Vienna, Department of Economics, Austria 2004 Spring Lecturer, Ajou University, Business School, South-Korea Affiliations 2011-present Research Affiliate, Ifo Institute, Center for Economic Studies (CESifo) 2009-present Research Affiliate, Barcelona Graduate School of Economics (BGSE) 2009-present Research Affiliate, Center for Economic Policy Research (CEPR) 2004-present Research Affiliate, Institute for the Study of Labor (IZA) Education 2004 Sept. Ph.D. in Economics, European University Institute, Florence: • Supervisor: Giuseppe Bertola • Thesis Committee: Samuel Bentolila, Omar Licandro, Christopher Pissarides 2002 Exchange Student, New York University, Economics Department, New York 2000 Master of Arts in Economics, EHESS, Delta, Paris 2000 Magistère in Economics, Sorbonne University, Paris I 1997 Master of Arts in Philosophy, Sorbonne University, Paris I 1996 Bachelor of Sciences in Logic, Sorbonne University, Paris I Updated January 2014 Julien Prat Fields of Interest Macroeconomics, Labor Economics, International Trade, Contract Theory Publications Articles in refereed journals 1. “Dynamic Incentive Contracts when Agent’s Quality is Unknown”, with Boyan Jovanovic, Forthcoming in Theoretical Economics 2. “Efficiency Gains from Trade and Labor Market Outcomes” with Gabriel Felbermayr, Nordic Economic Policy Review, 2013, Vol. -

Cesifo Working Paper No. 5150 Category 8: Trade Policy December 2014
Going Deep: The Trade and Welfare Effects of TTIP Rahel Aichele Gabriel Felbermayr Inga Heiland CESIFO WORKING PAPER NO. 5150 CATEGORY 8: TRADE POLICY DECEMBER 2014 An electronic version of the paper may be downloaded • from the SSRN website: www.SSRN.com • from the RePEc website: www.RePEc.org • from the CESifo website: www.CESifoT -group.org/wp T CESifo Working Paper No. 5150 Going Deep: The Trade and Welfare Effects of TTIP Abstract Since July 2013, the EU and the US have been negotiating a preferential trade agreement (PTA), the Transatlantic Trade and Investment Partnership (TTIP). We use a multi-country, multi-industry Ricardian trade model with national and international input-output linkages to quantify its potential economic consequences. We structurally estimate the sectoral trade flow elasticities of trade costs and of existing PTAs. We simulate the trade, value added, and welfare effects of the TTIP, assuming that the agreement would eliminate all transatlantic tariffs and reduce non-tariff barriers as other deep PTAs have. The long-run level of real per capita income would change by 2.12% in the EU, by 2.68% in the US, and by -0.03% in the rest of the world relative to the status quo. However, there is substantial heterogeneity across the 134 geographical entities that we investigate. Gross value of EU-US trade could triple, but its value added would grow by substantially less. Moreover, trade diversion effects are more pronounced in value added trade than in gross trade. This signals a deepening of the transatlantic value chain. JEL-Code: F130, F140, F170.