On the Relationship Between the Moyal Algebra and the Quantum
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Research Archive
http://dx.doi.org/10.1108/IJBM-05-2016-0075 View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by University of Hertfordshire Research Archive Research Archive Citation for published version: Dimitris Kakofengitis, Maxime Oliva, and Ole Steuernagel, ‘Wigner's representation of quantum mechanics in integral form and its applications’, Physical Review A, Vol. 95, 022127, published 27 February 2017. DOI: https://doi.org/10.1103/PhysRevA.95.022127 Document Version: This is the Accepted Manuscript version. The version in the University of Hertfordshire Research Archive may differ from the final published version. Users should always cite the published version of record. Copyright and Reuse: ©2017 American Physical Society. This manuscript version is made available under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited. Enquiries If you believe this document infringes copyright, please contact the Research & Scholarly Communications Team at [email protected] Wigner's representation of quantum mechanics in integral form and its applications Dimitris Kakofengitis, Maxime Oliva, and Ole Steuernagel School of Physics, Astronomy and Mathematics, University of Hertfordshire, Hatfield, AL10 9AB, UK (Dated: February 28, 2017) We consider quantum phase-space dynamics using Wigner's representation of quantum mechanics. We stress the usefulness of the integral form for the description of Wigner's phase-space current J as an alternative to the popular Moyal bracket. The integral form brings out the symmetries between momentum and position representations of quantum mechanics, is numerically stable, and allows us to perform some calculations using elementary integrals instead of Groenewold star products. -

Weyl Quantization and Wigner Distributions on Phase Space
faculteit Wiskunde en Natuurwetenschappen Weyl quantization and Wigner distributions on phase space Bachelor thesis in Physics and Mathematics June 2014 Student: R.S. Wezeman Supervisor in Physics: Prof. dr. D. Boer Supervisor in Mathematics: Prof. dr H. Waalkens Abstract This thesis describes quantum mechanics in the phase space formulation. We introduce quantization and in particular the Weyl quantization. We study a general class of phase space distribution functions on phase space. The Wigner distribution function is one such distribution function. The Wigner distribution function in general attains negative values and thus can not be interpreted as a real probability density, as opposed to for example the Husimi distribution function. The Husimi distribution however does not yield the correct marginal distribution functions known from quantum mechanics. Properties of the Wigner and Husimi distribution function are studied to more extent. We calculate the Wigner and Husimi distribution function for the energy eigenstates of a particle trapped in a box. We then look at the semi classical limit for this example. The time evolution of Wigner functions are studied by making use of the Moyal bracket. The Moyal bracket and the Poisson bracket are compared in the classical limit. The phase space formulation of quantum mechanics has as advantage that classical concepts can be studied and compared to quantum mechanics. For certain quantum mechanical systems the time evolution of Wigner distribution functions becomes equivalent to the classical time evolution stated in the exact Egerov theorem. Another advantage of using Wigner functions is when one is interested in systems involving mixed states. A disadvantage of the phase space formulation is that for most problems it quickly loses its simplicity and becomes hard to calculate. -

Phase-Space Description of the Coherent State Dynamics in a Small One-Dimensional System
Open Phys. 2016; 14:354–359 Research Article Open Access Urszula Kaczor, Bogusław Klimas, Dominik Szydłowski, Maciej Wołoszyn, and Bartłomiej J. Spisak* Phase-space description of the coherent state dynamics in a small one-dimensional system DOI 10.1515/phys-2016-0036 space variables. In this case, the product of any functions Received Jun 21, 2016; accepted Jul 28, 2016 on the phase space is noncommutative. The classical alge- bra of observables (commutative) is recovered in the limit Abstract: The Wigner-Moyal approach is applied to investi- of the reduced Planck constant approaching zero ( ! 0). gate the dynamics of the Gaussian wave packet moving in a ~ Hence the presented approach is called the phase space double-well potential in the ‘Mexican hat’ form. Quantum quantum mechanics, or sometimes is referred to as the de- trajectories in the phase space are computed for different formation quantization [6–8]. Currently, the deformation kinetic energies of the initial wave packet in the Wigner theory has found applications in many fields of modern form. The results are compared with the classical trajecto- physics, such as quantum gravity, string and M-theory, nu- ries. Some additional information on the dynamics of the clear physics, quantum optics, condensed matter physics, wave packet in the phase space is extracted from the analy- and quantum field theory. sis of the cross-correlation of the Wigner distribution func- In the present contribution, we examine the dynam- tion with itself at different points in time. ics of the initially coherent state in the double-well poten- Keywords: Wigner distribution, wave packet, quantum tial using the phase space formulation of the quantum me- trajectory chanics. -

P. A. M. Dirac and the Maverick Mathematician
Journal & Proceedings of the Royal Society of New South Wales, vol. 150, part 2, 2017, pp. 188–194. ISSN 0035-9173/17/020188-07 P. A. M. Dirac and the Maverick Mathematician Ann Moyal Emeritus Fellow, ANU, Canberra, Australia Email: [email protected] Abstract Historian of science Ann Moyal recounts the story of a singular correspondence between the great British physicist, P. A. M. Dirac, at Cambridge, and J. E. Moyal, then a scientist from outside academia working at the de Havilland Aircraft Company in Britain (later an academic in Australia), on the ques- tion of a statistical basis for quantum mechanics. A David and Goliath saga, it marks a paradigmatic study in the history of quantum physics. A. M. Dirac (1902–1984) is a pre- neering at the Institut d’Electrotechnique in Peminent name in scientific history. In Grenoble, enrolling subsequently at the Ecole 1962 it was my privilege to acquire a set Supérieure d’Electricité in Paris. Trained as of the letters he exchanged with the then a civil engineer, Moyal worked for a period young mathematician, José Enrique Moyal in Tel Aviv but returned to Paris in 1937, (1910–1998), for the Basser Library of the where his exposure to such foundation works Australian Academy of Science, inaugurated as Georges Darmois’s Statistique Mathéma- as a centre for the archives of the history of tique and A. N. Kolmogorov’s Foundations Australian science. This is the only manu- of the Theory of Probability introduced him script correspondence of Dirac (known to to a knowledge of pioneering European stud- colleagues as a very reluctant correspondent) ies of stochastic processes. -

The Moyal Equation in Open Quantum Systems
The Moyal Equation in Open Quantum Systems Karl-Peter Marzlin and Stephen Deering CAP Congress Ottawa, 13 June 2016 Outline l Quantum and classical dynamics l Phase space descriptions of quantum systems l Open quantum systems l Moyal equation for open quantum systems l Conclusion Quantum vs classical Differences between classical mechanics and quantum mechanics have fascinated researchers for a long time Two aspects: • Measurement process: deterministic vs contextual • Dynamics: will be the topic of this talk Quantum vs classical Differences in standard formulations: Quantum Mechanics Classical Mechanics Class. statistical mech. complex wavefunction deterministic position probability distribution observables = operators deterministic observables observables = random variables dynamics: Schrödinger Newton 2 Boltzmann equation for equation for state probability distribution However, some differences “disappear” when different formulations are used. Quantum vs classical First way to make QM look more like CM: Heisenberg picture Heisenberg equation of motion dAˆH 1 = [AˆH , Hˆ ] dt i~ is then similar to Hamiltonian mechanics dA(q, p, t) @A @H @A @H = A, H , A, H = dt { } { } @q @p − @p @q Still have operators as observables Second way to compare QM and CM: phase space representation of QM Most popular phase space representation: the Wigner function W(q,p) 1 W (q, p)= S[ˆ⇢](q, p) 2⇡~ iq0p/ Phase space S[ˆ⇢](q, p)= dq0 q + 1 q0 ⇢ˆ q 1 q0 e− ~ h 2 | | − 2 i Z The Weyl symbol S [ˆ ⇢ ]( q, p ) maps state ⇢ ˆ to a function of position and momentum (= phase space) Phase space The Wigner function is similar to the distribution function of classical statistical mechanics Dynamical equation = Liouville equation. -

About the Concept of Quantum Chaos
entropy Concept Paper About the Concept of Quantum Chaos Ignacio S. Gomez 1,*, Marcelo Losada 2 and Olimpia Lombardi 3 1 National Scientific and Technical Research Council (CONICET), Facultad de Ciencias Exactas, Instituto de Física La Plata (IFLP), Universidad Nacional de La Plata (UNLP), Calle 115 y 49, 1900 La Plata, Argentina 2 National Scientific and Technical Research Council (CONICET), University of Buenos Aires, 1420 Buenos Aires, Argentina; [email protected] 3 National Scientific and Technical Research Council (CONICET), University of Buenos Aires, Larralde 3440, 1430 Ciudad Autónoma de Buenos Aires, Argentina; olimpiafi[email protected] * Correspondence: nachosky@fisica.unlp.edu.ar; Tel.: +54-11-3966-8769 Academic Editors: Mariela Portesi, Alejandro Hnilo and Federico Holik Received: 5 February 2017; Accepted: 23 April 2017; Published: 3 May 2017 Abstract: The research on quantum chaos finds its roots in the study of the spectrum of complex nuclei in the 1950s and the pioneering experiments in microwave billiards in the 1970s. Since then, a large number of new results was produced. Nevertheless, the work on the subject is, even at present, a superposition of several approaches expressed in different mathematical formalisms and weakly linked to each other. The purpose of this paper is to supply a unified framework for describing quantum chaos using the quantum ergodic hierarchy. Using the factorization property of this framework, we characterize the dynamical aspects of quantum chaos by obtaining the Ehrenfest time. We also outline a generalization of the quantum mixing level of the kicked rotator in the context of the impulsive differential equations. Keywords: quantum chaos; ergodic hierarchy; quantum ergodic hierarchy; classical limit 1. -

Phase-Space Formulation of Quantum Mechanics and Quantum State
formulation of quantum mechanics and quantum state reconstruction for View metadata,Phase-space citation and similar papers at core.ac.uk brought to you by CORE ysical systems with Lie-group symmetries ph provided by CERN Document Server ? ? C. Brif and A. Mann Department of Physics, Technion { Israel Institute of Technology, Haifa 32000, Israel We present a detailed discussion of a general theory of phase-space distributions, intro duced recently by the authors [J. Phys. A 31, L9 1998]. This theory provides a uni ed phase-space for- mulation of quantum mechanics for physical systems p ossessing Lie-group symmetries. The concept of generalized coherent states and the metho d of harmonic analysis are used to construct explicitly a family of phase-space functions which are p ostulated to satisfy the Stratonovich-Weyl corresp on- dence with a generalized traciality condition. The symb ol calculus for the phase-space functions is given by means of the generalized twisted pro duct. The phase-space formalism is used to study the problem of the reconstruction of quantum states. In particular, we consider the reconstruction metho d based on measurements of displaced pro jectors, which comprises a numb er of recently pro- p osed quantum-optical schemes and is also related to the standard metho ds of signal pro cessing. A general group-theoretic description of this metho d is develop ed using the technique of harmonic expansions on the phase space. 03.65.Bz, 03.65.Fd I. INTRODUCTION P function [?,?] is asso ciated with the normal order- ing and the Husimi Q function [?] with the antinormal y ordering of a and a . -

Probability and Irreversibility in Modern Statistical Mechanics: Classical and Quantum
Probability and Irreversibility in Modern Statistical Mechanics: Classical and Quantum David Wallace July 1, 2016 Abstract Through extended consideration of two wide classes of case studies | dilute gases and linear systems | I explore the ways in which assump- tions of probability and irreversibility occur in contemporary statistical mechanics, where the latter is understood as primarily concerned with the derivation of quantitative higher-level equations of motion, and only derivatively with underpinning the equilibrium concept in thermodynam- ics. I argue that at least in this wide class of examples, (i) irreversibility is introduced through a reasonably well-defined initial-state condition which does not precisely map onto those in the extant philosophical literature; (ii) probability is explicitly required both in the foundations and in the predictions of the theory. I then consider the same examples, as well as the more general context, in the light of quantum mechanics, and demonstrate that while the analysis of irreversiblity is largely unaffected by quantum considerations, the notion of statistical-mechanical probability is entirely reduced to quantum-mechanical probability. 1 Introduction: the plurality of dynamics What are the dynamical equations of physics? A first try: Before the twentieth century, they were the equations of classical mechanics: Hamilton's equations, say, i @H @H q_ = p_i = − i : (1) @pi @q Now we know that they are the equations of quantum mechanics:1 1For the purposes of this article I assume that the Schr¨odingerequation -
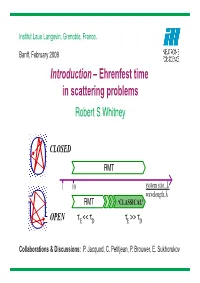
Introduction – Ehrenfest Time in Scattering Problems Robert S Whitney
Institut Laue Langevin, Grenoble, France. Banff, February 2008 Introduction – Ehrenfest time in scattering problems Robert S Whitney CLOSED RMT 1 10 system size, L wavelength,λ RMT ‘CLASSICAL’ OPEN τ << ττ >> τ E DDE Collaborations & Discussions: P. Jacquod, C. Petitjean, P. Brouwer, E. Sukhorukov When is quantum = classical ? QUANTUMEhrenfest theorem CLASSICAL Liouville theorem d ρˆ = −i¯h[Hˆ, ρˆ] d f(r, p)=−{H,f(r, p)} dt dt phase−space commutator Moyal bracket Poisson bracket Wigner function minimally dispersed W wavepacket 1/2 1/2 L deBoglie L,W L λ hyperbolic stretch non−hyperbolic stretch Quantum = Classical & fold Quantum = Classical Ehrenfest time (log time) Ehrenfest Time, τE: time during which 1/2 1/2 L,W = L λ deBoglie quantum classical τ =2Λ−1 ln[L/λ ] hyperbolic stretch non−hyperbolic stretch E deBroglie & fold Quantum = Classical 2 Quantum = Classical with L=L, (W /L) WAVEPACKET growth ∝ exp[−Λt] CLOSED SYSTEM – classical limit TIMESCALES: Form factor GUE − classical limit −1 ♣ (Level-spacing) ∝ (L/λdeBroglie) GOE ♣ ∝ L/λ OPEN SYSTEM Ehrenfest time ln[ deBroglie] Ehrenfest time "All" particles escape ♣ Classical scales: beforeh/∆ t dwell time = λdeBroglie-independent ‘CLASSICAL’ Brouwer−Rahav−Tian A short and inaccurate history of the Ehrenfest time! LAST CENTURY Ehrenfest: Ehrenfest theorem. = Liouville theorem Z. Physik 45 455 (1927) ??? Larkin-Ovchinnikov: superconducting fluct. in metals Sov. Phys. JETP 28 1200 (1969) Berman-Zaslavsky: stochasticity Physica A 91, 450 (1978), Phys. Rep. 80, 157 (1981) Aleiner-Larkin weak-loc. in transport & level-statistics PRB 54, 14423 (1996); 55, R1243 (1997). THIS CENTURY Semiclassics ... see other talks this week. -

Quantum Deformed Canonical Transformations, W {\Infty
UTS − DFT − 93 − 11 QUANTUM DEFORMED CANONICAL TRANSFORMATIONS, W∞-ALGEBRAS AND UNITARY TRANSFORMATIONS E.Gozzi♭ and M.Reuter♯ ♭ Dipartimento di Fisica Teorica, Universit`adi Trieste, Strada Costiera 11, P.O.Box 586, Trieste, Italy and INFN, Sezione di Trieste. ♯ Deutsches Elektronen-Synchrotron DESY, Notkestrasse 85, W-2000 Hamburg 52, Germany ABSTRACT We investigate the algebraic properties of the quantum counterpart of the classical canon- ical transformations using the symbol-calculus approach to quantum mechanics. In this framework we construct a set of pseudo-differential operators which act on the symbols of arXiv:hep-th/0306221v1 23 Jun 2003 operators, i.e., on functions defined over phase-space. They act as operatorial left- and right- multiplication and form a W∞ × W∞- algebra which contracts to its diagonal subalgebra in the classical limit. We also describe the Gel’fand-Naimark-Segal (GNS) construction in this language and show that the GNS representation-space (a doubled Hilbert space) is closely related to the algebra of functions over phase-space equipped with the star-product of the symbol-calculus. 1. INTRODUCTION The Dirac canonical quantization [1] can be considered as a map [2] [3]. ”D” sending real functions defined on phase space f1, f2, ··· to hermitian operators f1, f2 ··· which act on [2,3] some appropriate Hilbert space According to Dirac, this map shouldb satisfyb the following requirements (a) D λ1f1 + λ2f2 = λ1f1 + λ2f2, λ1,2 ∈ R 1 (b) D f1, f2 = f1b, f2 b pb ih¯ (1.1) (c) D 1 = I b b (d) q, p are represented irreducibly. b b Here ·, · pb denotes the Poisson bracket, and I is the unit operator. -

The Moyal-Lie Theory of Phase Space Quantum Mechanics
The Moyal-Lie Theory of Phase Space Quantum Mechanics T. Hakio˘glu Physics Department, Bilkent University, 06533 Ankara, Turkey and Alex J. Dragt Physics Department, University of Maryland, College Park MD 20742-4111, USA Abstract A Lie algebraic approach to the unitary transformations in Weyl quantization is discussed. This approach, being formally equivalent to the ?-quantization is an extension of the classical Poisson-Lie formalism which can be used as an efficient tool in the quantum phase space transformation theory. The purpose of this paper is to show that the Weyl correspondence in the quantum phase space can be presented in a quantum Lie algebraic perspective which in some sense derives analogies from the Lie algebraic approach to classical transformations and Hamiltonian vec- tor fields. In the classical case transformations of functions f(z) of the phase space z =(p, q) are generated by the generating functions µ(z). If the generating functions are elements of a set, then this set usually contains a subsetG closed under the action the Poisson Bracket (PB), so defining an algebra. To be more precise one talks about different representations of the generators and of the phase space algebras. The second well known representation is the so called adjoint representation of the Poisson algebra of the ’s in terms of the classical Gµ Lie generators L µ over the Lie algebra. These are the Hamiltonian vector fields with the G Hamiltonians µ. By Liouville’s theorem, they characterize an incompressible and covariant phase space flow.G The quantum Lie approach can be based on a parallelism with the classical one above. -

The Semiclassical Dirac Mechanics Alan R. Katz
UNIVERSITY OF CALIFORNIA Los Angeles Dequantization of the Dirac Equation: The Semiclassical Dirac Mechanics A dissertation submitted In partial satisfaction of the requirements for the degree Doctor of Philosophy in Physics by Alan R. Katz 1987 @ Copyright by Alan R. Katz 1987 TABLE OF CONTENTS Page ACKNOWLEDGEMENTS Vi VITA vii ABSTRACT OF THE DISSERTATION ix Chapter I. The Dirac Equation, g - 2 experiments, and the Semi-Classical Limit A. Introduction 1 B. Organization 6 c. Notation 8 Chapter II. Superfield WKB and Superspace Mechanics A. Introduction 10 B. WKB for an Ordinary Scalar Field 14 c. Mechanics in Superspace 17 D. WKB for a Superfield 23 E. WKB for the Dirac Equation Directly 26 Chapter Ill. Dequantization and *-Products A. Introduction 31 B. The Normal Order Map and *-Product 33 c. Dynamics and Equations of Motion 35 D. Example: A Scalar Particle 37 E. Gauge Invariance and the *-Product 38 iv Chapter IV. The Dirac Semlclassical Mechanics: Particle in a Homogeneous Electromagnetic Field A. The Dirac Semiclassical Mechanics 43 B. Dirac Mechanics and *-Dequantization 47 C. Dirac Particle in an External Homogeneous Field 53 D. The Modified Dirac Equation and the (g - 2) Terms 60 Chapter V. The Dirac Mechanics: Inhomogeneous Field 63 Chapter VI. Conclusions and Future Work 72 REFERENCES 75 APPENDICES A. Chapter II Notation 77 B. Superfield WKB 79 C. Coherent States 81 D. Phase Space Identities 85 E. Calculations for Chapter IV 87 F. Calculations for Chapter V 92 v ACKNOWLEDGEMENTS I would like to express my sincere thanks to Christian Fronsdal for his help, advice, support and patience during these many years.