Nitin Kapania CS 229 Final Project Predicting Fantasy Football
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Arkansas Razorbacks 2005 Football
ARKANSAS RAZORBACKS 2005 FOOTBALL HOGS TAKE ON TIGERS IN ANNUAL BATTLE OF THE BOOT: Arkansas will travel to Baton Rouge to take on the No. 3 LSU Tigers in the annual Battle of the Boot. The GAME 11 Razorbacks and Tigers will play for the trophy for the 10th time when the two teams meet at Tiger Stadium. The game is slated for a 1:40 p.m. CT kickoff and will be tele- Arkansas vs. vised by CBS Sports. Arkansas (4-6, 2-5 SEC) will be looking to parlay the momentum of back-to-back vic- tories over Ole Miss and Mississippi State into a season-ending win against the Tigers. Louisiana State LSU (9-1, 6-1 SEC) will be looking clinch a share of the SEC Western Division title Friday, Nov. 25, Baton Rouge, La. and punch its ticket to next weekend’s SEC Championship Game in Atlanta, Ga. 1:40 p.m. CT Tiger Stadium NOTING THE RAZORBACKS: * Arkansas and LSU will meet for the 51st time on the gridiron on Friday when the two teams meet in Baton Rouge. LSU leads the series 31-17-2 including wins in three of the Rankings: Arkansas (4-6, 2-5 SEC) - NR last four meetings. The Tigers have won eight of 13 meetings since the Razorbacks Louisiana State (9-1, 6-1 SEC) - (No. 3 AP/ entered the SEC in 1992. (For more on the series see p. 2) No. 3 USA Today) * For the 10th-consecutive year since its inception, Arkansas and LSU will be playing for The Coaches: "The Golden Boot," a trophy shaped like the two states combined. -

ROUND 3 (Weeks 9 - 12)
ROUND 3 (Weeks 9 - 12) TEAM NAME Quarterback Runningback Runningback Wide Receiver Wide Receiver Tight End Defense Kicker 49ers Tom Brady Leveon Bell David Johnson Marvin Jones Antonio Brown Kyle Rudolph Vikings Patriots Albatros Derek Carr Latavius Murray Matt Forte Dez Bryant Odell Beckham Rob Gronkowski Seahawks Ravens BearsDown Drew Brees Todd Gurley Leveon Bell Dez Bryant Odell Beckham Greg Olsen Cowboys Eagles Bradley Tanks Aaron Rodgers Ezekiel Elliott Demarco Murray Dez Bryant Jordy Nelson Greg Olsen Packers Raiders Brutus Bears Tom Brady Devonta Freeman Leveon Bell Julio Jones Antonio Brown Rob Gronkowski Broncos Packers Bullslayer Drew Brees Ezekiel Elliott Leveon Bell AJ Green Odell Beckham Greg Olsen Chiefs Eagles Cardinals Aaron Rodgers Eddie Lacy Adrian Peterson Julio Jones Antonio Brown Jimmy Graham Bills Seahawks Claim Destroyers Ben Roethlisberger Todd Gurley Adrian Peterson Julio Jones Antonio Brown Rob Gronkowski Steelers Patriots Clorox Clean Aaron Rodgers Ezekiel Elliott Leveon Bell Mike Evans Odell Beckham Greg Olsen Chiefs Colts Clueless Cam Newton Mark Ingram Adrian Peterson Odell Beckham Brandon Marshall Rob Gronkowski Eagles Raiders Cougars Andrew Luck Todd Gurley Adrian Peterson Julio Jones Antonio Brown Antonio Gates Packers Cowboys DaBears Drew Brees Ezekiel Elliott Demarco Murray Mike Evans Odell Beckham Greg Olsen Ravens Cowboys Danger Zone Cam Newton Todd Gurley Jamaal Charles Julio Jones Antonio Brown Rob Gronkowski Broncos Patriots DeForge to be Reckoned With Drew Brees Leveon Bell Demarco Murray Brandon -

2011 Topps Football 2011 Complete Set Hobby Edition
2011 TOPPS FOOTBALL 2011 COMPLETE SET HOBBY EDITION All 440 Base Cards including 110 Rookies from 2011 Topps Football BASE CARDS • 440 • Veterans: 262 NFL pros. • Rookies: 110 hopeful talents. • All-Pro: 2010 NFL First Team All-Pros. • Team Cards: 32 cards featuring each team in the league. • Rookie Premiere: 30 elite 2011 NFL Rookies pose for a HOBBY STORE BENEFITS team photo. • Appeals to Fans & Collectors! • Record Breakers: They made the record book in 2010. • Outstanding Value at a Great Price! • Super Bowl Champions: The Packers and the • Collectors Return Year After Year! Lombardi Trophy! • Ships September - The Start of the NFL Season! • League MVP: Tom Brady • 2010 Rookies Of The Year: Sam Bradford & Ndamukong Suh ® TM & © 2011 The Topps Company, Inc. Topps and Topps Football are trademarks of The Topps Company, Inc. All rights reserved. © 2011 NFL Properties, LLC. Team Names/Logos/Indicia are trademarks of the teams indicated. All other PLUS One 5-Card Pack of Hobby Exclusive NFL-related trademarks are trademarks of the National Football League. Officially Licensed Product of NFL PLAYERS | NFLPLAYERS.COM. Please note that you must obtain the approval of the National Football League Properties in promotional materials that incorporate any marks, designs, logos, etc. of the National Football League or any of its teams, unless the Numbered* Red Base Parallel Cards material is merely an exact depiction of the authorized product you purchase from us. Topps does not, in any manner, make any representations as to whether its cards will attain any future value. NO PURCHASE NECESSARY. PLUS ONE 5-CARD PACK OF HOBBY EXCLUSIVE NUMBERED RED BASE PARALLEL CARDS 2011 COMPLETE SET CHECKLIST 1 Aaron Rodgers 69 Tyron Smith 137 Team Card 205 John Kuhn 273 LeGarrette Blount 341 Braylon Edwards 409 D.J. -

2018 Nfl Season Begins on Kickoff Weekend
FOR IMMEDIATE RELEASE 9/4/18 http://twitter.com/nfl345 2018 NFL SEASON BEGINS ON KICKOFF WEEKEND The NFL returns this week and it’s time to get back to football. Kickoff Weekend signals the start of a 256-game journey, one that promises hope for each of the league’s 32 teams as they set their eyes on Super Bowl LIII, which will be played on Sunday, February 3, 2019 at Mercedes-Benz Stadium in Atlanta, GA. One thing is certain: the 2018 season will be filled with memorable moments, as young players emerge onto the scene, familiar faces continue their climb up the record books and teams vie to make their mark in the postseason. The 99th season of NFL play kicks off on Thursday night (NBC, 8:20 PM ET) as the Super Bowl champion PHILADELPHIA EAGLES host the ATLANTA FALCONS at Lincoln Financial Field in a battle of the NFC’s past two Super Bowl representatives. The Eagles, who finished last in the NFC East with a 7-9 record in 2016, became the second team since 2003 to go from “worst- to-first” en route to a Super Bowl victory, joining the 2009 New Orleans Saints. Every team enters the 2018 season with hope and a trip to Atlanta for Super Bowl LIII in mind. Below are a few reasons why. THE FIELD IS OPEN: Five of the eight divisions in 2017 were won by a team that finished in third or fourth place in the division the previous season – Jacksonville (AFC South), the Los Angeles Rams (NFC West), Minnesota (NFC North), New Orleans (NFC South) and Philadelphia (NFC East). -

GARY KUBIAK HEAD COACH – 22Nd NFL Season (12Th with Broncos)
GARY KUBIAK HEAD COACH – 22nd NFL Season (12th with Broncos) Gary Kubiak, a 23-year coaching veteran and three-time Super Bowl champion, enters his third decade with the Denver Broncos after being named the 15th head coach in club history on Jan. 19, 2015. A backup quarterback for nine seasons (1983-91) with the Broncos and an offensive coordinator for 11 years (1995- 2005) with the club, Kubiak returns to Denver after spending eight years (2006-13) as head coach of the Houston Texans and one season (2014) as offensive coordinator with the Baltimore Ravens. During 21 seasons working in the NFL, Kubiak has coached 30 players to a total of 57 Pro Bowl selections. He has appeared in eight conference championship games and six Super Bowls as a player or coach and was part of three World Championship staffs (S.F., 1994; Den., 1997-98) as a quarterbacks coach or offensive coordinator. In his most recent position as Baltimore’s offensive coordinator in 2014, he oversaw one of the NFL’s most improved and explosive units to help the Ravens advance to the AFC Divisional Playoffs. His offense posted the third-largest overall improvement (+57.5 ypg) in the NFL from the previous season and posted nearly 50 percent more big plays (74 plays of 20+yards) from the year before he arrived. Ravens quarterback Joe Flacco recorded career highs in passing yards (3,986) and touchdown passes (27) under Kubiak’s guidance while running back Justin Forsett ranked fifth in the league in rushing (1,266 yds.) to earn his first career Pro Bowl selection. -

We're Not Rookies Anymore Fantasy Lea Draft Results 24-Oct-2012 02:56 PM ET
RealTime Fantasy Sports We're Not Rookies Anymore Fantasy Lea Draft Results 24-Oct-2012 02:56 PM ET We're Not Rookies Anymore Fantasy Leauge Draft Sun., Aug 19 2012 4:22:02 PM Rounds: 14 Round 1 Round 5 1. Kruppa - Aaron Rodgers QB, GNB 1. Kruppa - Roddy White WR, ATL 2. THE BONE COLECTOR - Drew Brees QB, NOR 2. THE BONE COLECTOR - Victor Cruz WR, NYG 3. michaels marauders - Arian Foster RB, HOU 3. michaels marauders - Jermichael Finley TE, GNB 4. Rebekahs Rejects - Cam Newton QB, CAR 4. Rebekahs Rejects - Shonn Greene RB, NYJ 5. Todd - Calvin Johnson WR, DET 5. Todd - Matt Ryan QB, ATL 6. Paul - Wes Welker WR, NWE 6. Paul - Vernon Davis TE, SFO 7. THE REAL DEAL - Tom Brady QB, NWE 7. THE REAL DEAL - Brandon Pettigrew TE, DET 8. KRISTEN DIAMONDS - Matthew Stafford QB, DET 8. KRISTEN DIAMONDS - Owen Daniels TE, HOU 9. 3sheatstodawind - Eli Manning QB, NYG 9. 3sheatstodawind - Hakeem Nicks WR, NYG 10. Matadors - Peyton Manning QB, DEN 10. Matadors - Brandon Marshall WR, CHI Round 2 Round 6 1. Matadors - Ray Rice RB, BAL 1. Matadors - Coby Fleener TE, IND 2. 3sheatstodawind - LeSean McCoy RB, PHI 2. 3sheatstodawind - Jason Witten TE, DAL 3. KRISTEN DIAMONDS - Darren Sproles RB, NOR 3. KRISTEN DIAMONDS - C.J. Spiller RB, BUF 4. THE REAL DEAL - Chris Johnson RB, TEN 4. THE REAL DEAL - Dwayne Bowe WR, KAN 5. Paul - Philip Rivers QB, SDG 5. Paul - Ahmad Bradshaw RB, NYG 6. Todd - Andre Johnson WR, HOU 6. Todd - Tony Gonzalez TE, ATL 7. Rebekahs Rejects - Kendall Hunter RB, SFO 7. -
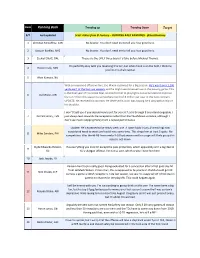
Running Back Trending up Trending Down Target
Rank Running Back Trending up Trending Down Target 9/7 Last updated Scott Atkins from SI Fantasy – RUNNING BACK RANKINGS - @ScottFantasy 1 Christian McCaffrey, CAR No brainer. You don't need me to tell you how good he is. 2 Saquon Barkley, NYG No brainer. You don't need me to tell you how good he is. 3 Ezekiel Elliott, DAL These are the ONLY three backs I'd take before Michael Thomas. I'm perfectly okay with you reversing this tier, but when Cook is on the field, I think he 4 Dalvin Cook, MIN justifies this draft capital. 5 Alvin Kamara, NO With an improved offensive line, Joe Mixon is primed for a big season. He's went over 1,100 yards each of the last two seasons and he might see increased use in the passing game. This is the final year of his rookie deal, so look for him to play lights out as he seeks to improve 6 Joe Mixon, CIN the 1.2 million this season to somewhere north of 8 million per year in the next contract. UPDATE: He received his contract. He deserved it, but I was hoping he'd play with a chip on his shoulder. I won't fault you if you decide Henry isn't for you at 7, as 6 through 9 are interchangeable. I 7 Derrick Henry, TEN just always lean towards the receptions rather than the Touchdown variance, although I don't see much stopping Henry from a repeat performance. Update: He's expected to be ready week one. -

2011 TOPPS FINEST FOOTBALL Checklist
2011 TOPPS FINEST FOOTBALL April 2011 Checklist AUTOGRAPH PATCH/RELIC CARDS Rookie Autograph Patch Cards TATR-LWM Ray Lewis 1-35 TBD Patrick Willis Jerod Mayo Rookie Jumbo Patch Autograph Cards TATR1-7 TBD Rookies & Veterans 1-20 TBD AUTOGRAPH CARDS Autograph JUMBO Relic Cards On-Card Rookie Autograph Cards FAJR-DB Drew Brees 1-35 TBD Rookies FAJR-GJ Greg Jennings FAJR-JK Johnny Knox Finest Moments Autograph Cards FAJR-KM Knowshon Moreno FMA-MS Mark Sanchez FAJR-LM LeSean McCoy FMA-AP Adrian Peterson FAJR-ML Marshawn Lynch FMA-PH Peyton Hillis FAJR-MV Michael Vick FMA-TJ Thomas Jones FAJR-PW Patrick Willis FMA-JG Jabar Gaffney FAJR-RM Rashard Mendenhall FMA1-20 TBD Rookies & Veterans FAJR-RW Roddy White FAJR-SH Santonio Holmes INSERT CARDS FAJR-SR Sidney Rice Rookie Finest Atomic Refractor Cards FAJR1-38 TBD Rookies & Veterans 1-25 TBD Rookies Dual Autograph Dual Relic Cards Finest Moments DADR-TBD Sam Bradford FM-MS Mark Sanchez TBD Rookie FM-AP Adrian Peterson DADR-TBD Tim Tebow FM-PH Peyton Hillis TBD Rookie FM-TJ Thomas Jones DADR-TBD Dez Bryant FM-JG Jabar Gaffney TBD Rookie FM1-20 TBD Rookies & Veterans DADR1-17 TBD Rookies & Veterans BASE CARDS 1 Michael Vick Triple Relic Triple Autograph Cards 2 Pierre Garcon TATR-VMJ Michael Vick 3 Jeremy Maclin LeSean McCoy 4 Mike Wallace DeSean Jackson 5 Jahvid Best TATR-GWC Antonio Gates 6 Vernon Davis Jason Witten 7 Rookie Chris Cooley 8 Greg Jennings 9 Santana Moss 10 Adrian Peterson Preliminary Checklist Subject to Change 2011 TOPPS FINEST FOOTBALL April 2011 Checklist BASE CARDS (cont.) -

2Nd Swing Golf Playoff Week 2 26-Feb-2010 10:50 PM Eastern
www.rtsports.com 2nd Swing Golf Playoff Week 2 26-Feb-2010 10:50 PM Eastern BIG BIG TUNA!! - Chad Miller Mr. Minneapolis - Tyler Bauman Peyton Manning QB IND vs NYJ * 286 19.07 Kurt Warner QB ARI vs STL * 229 15.27 LaDainian Tomlinson RB SDG @ TEN * 165 11.00 Frank Gore RB SFO vs DET * 242 16.13 Joseph Addai RB IND vs NYJ * 234 15.60 Chris Johnson RB TEN vs SDG * 353 23.53 Chad Ochocinco WR CIN vs KAN * 222 14.80 Wes Welker WR NWE vs JAC * 276 18.40 Andre Johnson WR HOU @ MIA * 294 19.60 Roddy White WR ATL vs BUF * 241 16.07 Miles Austin WR DAL @ WAS * 259 17.27 Vincent Jackson WR SDG @ TEN * 234 15.60 John Carlson TE SEA @ GNB * 134 8.93 Jason Witten TE DAL @ WAS * 182 12.13 Mason Crosby K GNB vs SEA * 122 8.13 Ryan Longwell K MIN @ CHI * 118 7.87 Minnesota Vikings D/ST MIN @ CHI * 87 5.80 San Francisco 49ers D/ST SFO vs DET * 103 6.87 Brett Favre QB MIN @ CHI 256 17.07 Eli Manning QB NYG vs CAR 239 15.93 Donovan McNabb QB PHI vs DEN 228 15.20 Vince Young QB TEN vs SDG 132 8.80 Brandon Jacobs RB NYG vs CAR 144 9.60 Jamal Lewis RB CLE vs OAK 61 4.07 Darren Sproles RB SDG @ TEN 156 10.40 Cedric Benson RB CIN vs KAN 180 12.00 Rashard Mendenhall RB PIT vs BAL 181 12.07 Marion Barber RB DAL @ WAS 161 10.73 Mike Sims-Walker WR JAC @ NWE 180 12.00 Kevin Walter WR HOU @ MIA 116 7.73 Sebastian Janikowski K OAK @ CLE 88 5.87 Lee Evans WR BUF @ ATL 127 8.47 Green Bay Packers D/ST GNB vs SEA 102 6.80 Kellen Winslow TE TAM @ NOR 178 11.87 Hitmen - Brent Louden Ohh Cueso - Kellen Krause Tom Brady QB NWE vs JAC * 269 17.93 Aaron Rodgers QB GNB vs SEA -

2006 TENNESSEE VOLUNTEERS FOOTBALL Contacts: Bud Ford (Cell 865-567-6287) Assoc
2006 TENNESSEE VOLUNTEERS FOOTBALL Contacts: Bud Ford (cell 865-567-6287) Assoc. AD-Media Relations John Painter (cell 865-414-1143) Assoc. SID P.O. Box 15016 Knoxville, TN 37901 Phone: (865) 974-1212 Fax: (865) 974-1269 [email protected] [email protected] 2006 TENNESSEE SCHEDULE Game 7 Date Opponent Time/Result Sept. 2 California [ESPN] W 35-18 Tennessee Volunteers (5-1) vs. Alabama Crimson Tide (5-2) Sept. 9 Air Force [VideoSeat PPV] W 31-30 Oct. 21 Neyland Stadium (102,038) 3:30 p.m. ET CBS Sept. 16 *Florida [CBS] L 20-21 Sept. 23 Marshall [VideoSeat PPV] W 33-7 RANKINGS: Tennessee is ranked No. 7 by the Associated Press and No. 9 by USA Today. Alabama is unranked. Sept. 30 at Memphis [ESPN] W 41-7 The game will be broadcast by the 80-plus station Vol Radio Network. For a complete list of stations, visit Oct. 7 *at Georgia [ESPN] W 51-33 RADIO: Oct. 21 *Alabama [CBS] 3:30 p.m. ET UTsports.com. Play-by-play broadcaster Bob Kesling is in his eighth season as the voice of the Volunteers and calls the Oct. 28 *at South Carolina [ESPN or ESPN2] 7:45 p.m. ET action along with Tim Priest and sideline reporter Jeff Francis. For the Crimson Tide Sports Network, play-by-play broad- Nov. 4 *LSU caster Eli Gold has the call along with Ken Stabler and Tom Roberts. Sirius satellite radio also will broadcast the game Nov. 11 *at Arkansas on channel 143 (UT feed). Nov. -

Todd Gurley: Rushing Into the Record Book
NFC NOTES FOR USE AS DESIRED FOR ADDITIONAL INFORMATION, 11/3/15 CONTACT: RANDALL LIU http://twitter.com/NFL345 TODD GURLEY: RUSHING INTO THE RECORD BOOK The St. Louis Rams selected running back TODD GURLEY in the first round of the 2015 NFL Draft. Just five games into his NFL career, Gurley is already making his mark in the NFL’s record book. “Todd is a special player,” says Rams general manager LES SNEAD, who drafted Gurley with the 10th overall pick. Since making his first career start in Week 4 at Arizona, Gurley has registered at least 125 rushing yards in four consecutive games. He is the first rookie in NFL history to rush for at least 125 yards in four games in a row. “Guys like Todd come around once every 10 years,” says St. Louis head coach JEFF FISHER. “Look at his explosion and change of direction, plus his football instincts. He loves football. He loves his teammates. That’s what he’s all about. He’s about winning football games and trying to contribute.” A look at Gurley’s first four career starts: DATE WEEK OPPONENT ATT. YARDS AVG. LONG TDs 10/4/15 4 at Arizona 19 146 7.7 52 0 10/11/15 5 at Green Bay 30 159 5.3 55 0 10/25/15 7 Cleveland 19 128 6.7 48 2 11/1/15 8 San Francisco 20 133 6.7 71t 1 “Todd Gurley is the premier player on that offense right now,” says NFL Network analyst and former Pro Bowl running back LA DAINIAN TOMLINSON. -

NFL Depth Chart Cheat Sheet
2010 NFL Fantasy Depth Charts Bills Dolphins Patriots Jets QB1 Trent Edwards QB1 Chad Henne QB1 Tom Brady QB1 Mark Sanchez QB2 Ryan Fitzpatrick QB2 Tyler Thigpen QB2 Brian Hoyer QB2 Mark Brunell RB1 C.J. Spiller RB1 Ronnie Brown RB1 Laurence Maroney RB1 Shonn Greene RB2 Fred Jackson RB2 Ricky Williams RB2 Fred Taylor RB2 LaDainian Tomlinson RB3 Marshawn Lynch RB3 Lex Hilliard RB3 Sammy Morris RB3 Joe McKnight WR1 Lee Evans WR1 Brandon Marshall WR1 Randy Moss WR1 Braylon Edwards WR2 Steve Johnson WR2 Brian Hartline WR2 Wes Welker WR2 Santonio Holmes* WR3 Roscoe Parrish WR3 Davone Bess WR3 Julian Edelman WR3 Jerricho Cotchery AFCEAST WR4 David Nelson WR4 Patrick Turner WR4 Brandon Tate WR4 David Clowney TE1 Jonathan Stupar TE1 Anthony Fasano TE1 Rob Gronkowski TE1 Dustin Keller TE2 Shawn Nelson* TE2 John Nalbone TE2 Aaron Hernandez TE2 Ben Hartsock K Rian Lindell K Dan Carpenter K Stephen Gostkowski K Nick Folk Ravens Bengals Browns Steelers QB1 Joe Flacco QB1 Carson Palmer QB1 Jake Delhomme QB1 Ben Roethlisberger* QB2 Marc Bulger QB2 J.T. O'Sullivan QB2 Seneca Wallace QB2 Dennis Dixon RB1 Ray Rice RB1 Cedric Benson RB1 Jerome Harrison RB1 Rashard Mendenhall RB2 Willis McGahee RB2 Bernard Scott RB2 Peyton Hillis RB2 Mewelde Moore RB3 Le'Ron McClain RB3 Brian Leonard RB3 James Davis RB3 Isaac Redman WR1 Anquan Boldin WR1 Chad Ochocinco WR1 Mohamed Massaquoi WR1 Hines Ward WR2 Derrick Mason WR2 Terrell Owens WR2 Josh Cribbs WR2 Mike Wallace WR3 T.J. Houshmandzadeh WR3 Andre Caldwell WR3 Chansi Stuckey WR3 Antwaan Randle El AFCNORTH WR4 Donte'