Characteristics of I/O Traffic in Personal Computer and Server
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Analysis of Server-Smartphone Application Communication Patterns
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Aaltodoc Publication Archive Aalto University School of Science Degree Programme in Computer Science and Engineering Péter Somogyi Analysis of server-smartphone application communication patterns Master’s Thesis Budapest, June 15, 2014 Supervisors: Professor Jukka Nurminen, Aalto University Professor Tamás Kozsik, Eötvös Loránd University Instructor: Máté Szalay-Bekő, M.Sc. Ph.D. Aalto University School of Science ABSTRACT OF THE Degree programme in Computer Science and MASTER’S THESIS Engineering Author: Péter Somogyi Title: Analysis of server-smartphone application communication patterns Number of pages: 83 Date: June 15, 2014 Language: English Professorship: Data Communication Code: T-110 Software Supervisor: Professor Jukka Nurminen, Aalto University Professor Tamás Kozsik, Eötvös Loránd University Instructor: Máté Szalay-Bekő, M.Sc. Ph.D. Abstract: The spread of smartphone devices, Internet of Things technologies and the popularity of web-services require real-time and always on applications. The aim of this thesis is to identify a suitable communication technology for server and smartphone communication which fulfills the main requirements for transferring real- time data to the handheld devices. For the analysis I selected 3 popular communication technologies that can be used on mobile devices as well as from commonly used browsers. These are client polling, long polling and HTML5 WebSocket. For the assessment I developed an Android application that receives real-time sensor data from a WildFly application server using the aforementioned technologies. Industry specific requirements were selected in order to verify the usability of this communication forms. The first one covers the message size which is relevant because most smartphone users have limited data plan. -

Implementation of Embedded Web Server Based on ARM11 and Linux Using Raspberry PI
International Journal of Recent Technology and Engineering (IJRTE) ISSN: 2277-3878, Volume-3 Issue-3, July 2014 Implementation of Embedded Web Server Based on ARM11 and Linux using Raspberry PI Girish Birajdar Abstract— As ARM processor based web servers not uses III. HARDWARE USED computer directly, it helps a lot in reduction of cost. In this We will use different hardware to implement this embedded project our aim is to implement an Embedded Web Server (EWS) based on ARM11 processor and Linux operating system using web server, which are described in this section. Raspberry Pi. it will provide a powerful networking solution with 1. Raspberry Pi : The Raspberry Pi is low cost ARM wide range of application areas over internet. We will run web based palm-size computer. The Raspberry Pi has server on an embedded system having limited resources to serve microprocessor ARM1176JZF-S which is a member of embedded web page to a web browser. ARM11 family and has ARMv6 architecture. It is build Index Terms— Embedded Web Server, Raspberry Pi, ARM, around a BCM2835 broadcom processor. ARM processor Ethernet etc. operates at 700 MHz & it has 512 MB RAM. It consumes 5V electricity at 1A current due to which power I. INTRODUCTION consumption of raspberry pi is less. It has many peripherals such as USB port, 10/100 ethernet, GPIO, HDMI & With evolution of World-Wide Web (WWW), its composite video outputs and SD card slot.SD card slot is application areas are increasing day by day. Web access used to connect the SD card which consist of raspberry linux functionality can be embedded in a low cost device which operating system. -

Data Management for Portable Media Players
Data Management for Portable Media Players Table of Contents Introduction..............................................................................................2 The New Role of Database........................................................................3 Design Considerations.................................................................................3 Hardware Limitations...............................................................................3 Value of a Lightweight Relational Database.................................................4 Why Choose a Database...........................................................................5 An ITTIA Solution—ITTIA DB........................................................................6 Tailoring ITTIA DB for a Specific Device......................................................6 Tables and Indexes..................................................................................6 Transactions and Recovery.......................................................................7 Simplifying the Software Development Process............................................7 Flexible Deployment................................................................................7 Working with ITTIA Toward a Successful Deployment....................................8 Conclusion................................................................................................8 Copyright © 2009 ITTIA, L.L.C. Introduction Portable media players have evolved significantly in the decade that has -

Microcomputers: NQS PUBLICATIONS Introduction to Features and Uses
of Commerce Computer Science National Bureau and Technology of Standards NBS Special Publication 500-110 Microcomputers: NQS PUBLICATIONS Introduction to Features and Uses QO IGf) .U57 500-110 NATIONAL BUREAU OF STANDARDS The National Bureau of Standards' was established by an act ot Congress on March 3, 1901. The Bureau's overall goal is to strengthen and advance the Nation's science and technology and facilitate their effective application for public benefit. To this end, the Bureau conducts research and provides; (1) a basis for the Nation's physical measurement system, (2) scientific and technological services for industry and government, (3) a technical basis for equity in trade, and (4) technical services to promote public safety. The Bureau's technical work is per- formed by the National Measurement Laboratory, the National Engineering Laboratory, and the Institute for Computer Sciences and Technology. THE NATIONAL MEASUREMENT LABORATORY provides the national system of physical and chemical and materials measurement; coordinates the system with measurement systems of other nations and furnishes essential services leading to accurate and uniform physical and chemical measurement throughout the Nation's scientific community, industry, and commerce; conducts materials research leading to improved methods of measurement, standards, and data on the properties of materials needed by industry, commerce, educational institutions, and Government; provides advisory and research services to other Government agencies; develops, produces, and -

Usb Laptop Console 2
QUICK SETUP GUIDE KVT100A-FT USB LAPTOP CONSOLE 2 24/7 TECHNICAL SUPPORT AT 1.877.877.2269 OR VISIT BLACKBOX.COM PACKAGE CONTENTS: The USB Laptop Console 2 is an adapter which enables you to control any computer with USB ports and a VGA video output, using just your • Second-Gen USB Laptop Console laptop. (Computer systems with DVI, HDMI or DisplayPort video will • (1x) 6 ft.(1.8m) high speed USB-A to require a DVI to VGA, HDMI to VGA or DisplayPort to VGA adapter.) USB-miniB cable The USB Laptop Console 2 streams real-time video over high-speed • (1x) flash drive with software and USB, from the host computer (server) to the application software you Users Manual (PDF) will install on your laptop. At the same time, the software emulates • Quick setup guide (printed) the server’s USB keyboard and mouse. A window on your laptop acts as a console and gives you easy and complete control over the server. It works even if the server is in the BIOS, or is otherwise damaged. No software is ever installed on the server. The USB Laptop Console 2 can be hot-plugged into a working system at any time. 1.877.877.2269 BLACKBOX.COM NEED HELP? QUICK SETUP GUIDE LEAVE THE TECH TO US KVT100A-FT LIVE 24/7 TECHNICAL SUPPORT USB LAPTOP CONSOLE 2 1.877.877.2269 Software Installation: Before installing the software in a Windows or Apple computer, please ensure the USB Laptop Console 2 is DISCONNECTED. Cancel any “Add new hardware” dialog screens as these can interfere with the installation process. -

TIBCO Spotfire® Analyst Portable Software Release 10.4 2
TIBCO Spotfire® Analyst Portable Software Release 10.4 2 Important Information SOME TIBCO SOFTWARE EMBEDS OR BUNDLES OTHER TIBCO SOFTWARE. USE OF SUCH EMBEDDED OR BUNDLED TIBCO SOFTWARE IS SOLELY TO ENABLE THE FUNCTIONALITY (OR PROVIDE LIMITED ADD-ON FUNCTIONALITY) OF THE LICENSED TIBCO SOFTWARE. THE EMBEDDED OR BUNDLED SOFTWARE IS NOT LICENSED TO BE USED OR ACCESSED BY ANY OTHER TIBCO SOFTWARE OR FOR ANY OTHER PURPOSE. USE OF TIBCO SOFTWARE AND THIS DOCUMENT IS SUBJECT TO THE TERMS AND CONDITIONS OF A LICENSE AGREEMENT FOUND IN EITHER A SEPARATELY EXECUTED SOFTWARE LICENSE AGREEMENT, OR, IF THERE IS NO SUCH SEPARATE AGREEMENT, THE CLICKWRAP END USER LICENSE AGREEMENT WHICH IS DISPLAYED DURING DOWNLOAD OR INSTALLATION OF THE SOFTWARE (AND WHICH IS DUPLICATED IN THE LICENSE FILE) OR IF THERE IS NO SUCH SOFTWARE LICENSE AGREEMENT OR CLICKWRAP END USER LICENSE AGREEMENT, THE LICENSE(S) LOCATED IN THE “LICENSE” FILE(S) OF THE SOFTWARE. USE OF THIS DOCUMENT IS SUBJECT TO THOSE TERMS AND CONDITIONS, AND YOUR USE HEREOF SHALL CONSTITUTE ACCEPTANCE OF AND AN AGREEMENT TO BE BOUND BY THE SAME. ANY SOFTWARE ITEM IDENTIFIED AS THIRD PARTY LIBRARY IS AVAILABLE UNDER SEPARATE SOFTWARE LICENSE TERMS AND IS NOT PART OF A TIBCO PRODUCT. AS SUCH, THESE SOFTWARE ITEMS ARE NOT COVERED BY THE TERMS OF YOUR AGREEMENT WITH TIBCO, INCLUDING ANY TERMS CONCERNING SUPPORT, MAINTENANCE, WARRANTIES, AND INDEMNITIES. DOWNLOAD AND USE OF THESE ITEMS IS SOLELY AT YOUR OWN DISCRETION AND SUBJECT TO THE LICENSE TERMS APPLICABLE TO THEM. BY PROCEEDING TO DOWNLOAD, INSTALL OR USE ANY OF THESE ITEMS, YOU ACKNOWLEDGE THE FOREGOING DISTINCTIONS BETWEEN THESE ITEMS AND TIBCO PRODUCTS. -

Embedded ATMEL HTTP Server
Embedded ATMEL HTTP Server A Design Project Report Presented to the Engineering Division of the Graduate School of Cornell University in Partial Fulfillment of the Requirements for the Degree of Masters of Engineering (Electrical) by Tzeming Tan, Jeremy Project Advisor: Dr. Bruce R. Land Degree date: May 2004 Abstract Master of Electrical and Computer Engineering Program Cornell University Design Project Report Project Title: Embedded ATMEL HTTP Server Author: Tzeming Tan, Jeremy Abstract: The objective of this project was to design and build an embedded HTTP server using a microcontroller chip. The webserver required the implementation of the interface with Ethernet as well as several internet protocols such as TCP/IP and ARP. This embedded web server is able to serve small, static web pages as well as perform certain useful laboratory lab functions such as displaying the current temperature read by the microcontroller from a thermometer, on the webpage. While the capabilities of the embedded webserver are no where near that of a regular server computer, its small size and relatively low cost makes it more practical for some applications. The web server was built, tested to work, and a temperature reporting feature added to it. Report Approved by Project Advisor: ___________________________________ Date: __________ ii Executive Summary The internet is a versatile, convenient and efficient means of communication in the 21st century. Protocols such as TCP/IP, UDP, DHCP and ICMP form the backbone of internet communications a large bulk of which consists of Hyper Text Transfer Protocol (HTTP) traffic for the World Wide Web. A HTTP or web server is a server process running at a web site which sends out web pages in response to HTTP requests from remote browsers. -

Chapter 16 Client/Server Computing
Client/Server Computing e RPC Slides are mainly taken from «O perating Systems: Internals and Design Principles”, 8/E William Stallings (Chapter 16). Sistemi di Calcolo (II semestre) – Roberto Baldoni Client/Server Computing • Client machines are generally single-user PCs or workstations that provide a highly user-friendly interface to the end user • Each server provides a set of shared services to the clients • The server enables many clients to share access to the same database and enables the use of a high-performance computer system to manage the database Generic Client/Server Environment Client/Server Applications • Basic software is an operating system running on the hardware platform • Platforms and the operating systems of client and server may differ • These lower-level differences are irrelevant as long as a client and server share the same communications protocols and support the same applications Generic Client/Server Architecture Client/Server Applications • Bulk of applications software executes on the server • Application logic is located at the client • Presentation services in the client Database Applications • The server is a database server • Interaction between client and server is in the form of transactions – the client makes a database request and receives a database response • Server is responsible for maintaining the database Client/Server Architecture for Database Applications Client/Server Database Usage Client/Server Database Usage Classes of Client/Server Applications • Host-based processing – Not true client/server -
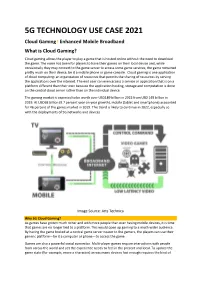
5G Technology Use Case 2021
5G TECHNOLOGY USE CASE 2021 Cloud Gaming l Enhanced Mobile Broadband What is Cloud Gaming? Cloud gaming allows the player to play a game that is hosted online without the need to download the game. The norm has been for players to have their games on their local device and, while occasionally they may connect to the game server to access some game services, the game remained pretty much on their device, be it a mobile phone or game console. Cloud gaming is one application of cloud computing: an organization of resources that permits the sharing of resources by serving the applications over the internet. The end user can even access a service or application that is on a platform different than their own because the application hosting, storage and computation is done on the central cloud server rather than on the individual device. The gaming market is expected to be worth over USD189 billion in 2022 from USD 149 billion in 2019. At USD68 billion (9.7 percent year on year growth), mobile (tablet and smartphone) accounted for 46 percent of the games market in 2019. This trend is likely to continue in 2022, especially so with the deployments of 5G networks and devices. Image Source: Arts Technica Why 5G Cloud Gaming? As games have gotten much richer and with more people than ever having mobile devices, it is time that games are no longer tied to a platform. This would open up gaming to a much wider audience. By having the game hosted at a central game server nearer to the gamers, the players can use their generic platform—be it a computer or phone—to access the game. -

Laptop-To-Server KVM Console with Rugged Housing
Laptop-to-Server KVM Console with Rugged Housing Product ID: NOTECONS02X This rugged and portable USB crash cart adapter lets you turn your laptop into a portable console for accessing servers, desktops and laptops, as well as ATMs, kiosks or any computing device that features both VGA and USB ports. This adapter also supports local file transfer and video capturing built into the software. Maximum durability This crash cart adapter has been specifically designed for maximum durability. It features a rugged, rubberized housing that can handle drops by absorbing shock, to make sure that you’re equipped for unexpected challenges. Hassle-free operation Troubleshoot your devices quickly and easily. Simply connect the crash cart adapter to your laptop using the included USB cable, then connect the integrated USB and VGA cables to your server. www.startech.com 1 800 265 1844 The crash cart adapter features a flexible software interface that offers robust performance. It enables you to transfer files from your laptop to the server, monitor and capture activity from the connected device as video for records or instructional purposes, and take screenshots and scale the display window to full-screen mode or smaller, without scroll bars. Compact portability This compact crash cart adapter lets you connect to a headless device using only a laptop, eliminating the need to lug around an awkward, traditional server room crash cart. With optimal portability in mind for your mobile administration or repairs, this pocket-sized adapter features a small footprint and lightweight design that easily fits inside your laptop bag. The adapter is USB powered so you won't need to carry a power adapter. -

Information Technology Support Specialist III
POSITION DESCRIPTION Information Technology Support Specialist III Position ............................ Information Technology Support Specialist III Department/Site ............... Technology and Computer Services FLSA ................................. Non-Exempt Evaluated by .................... Technical Operations Support Services Supervisor Salary Range ................... 52 Summary Plans, administers, and maintains all components of the local area and wide area networks governing the data communications among personal computers. This includes computer networks and related operating systems, mail and note systems, and telecommunications for microcomputers and servers. Plans and designs the implementation of the network infrastructure including hardware/software recommendations. Provides advanced technical support and help functions that relate to networks, security, redundancy, and connectivity. Essential Duties and Responsibilities - Participates in formulating, developing, and implementing integrated network architectures for large networked computer systems. Provides planning and advanced technical expertise for computer and network services for both local and wide area networks, and the internet. Develops specifications and functional requirements for networks including those for administrative and institutional use. - Administers, implements, and maintains the network including operations planning and design, work order generation, moves, adds, changes, fault prediction, trouble detection/correction, traffic measurement, circuit -

Versity Smartphone Series Spectralink Applications
Versity Smartphone Series Spectralink Applications Built-In applications for optimization that separate Spectralink devices apart from the competition The Versity Smartphone series comes preloaded with a range of essential Applications for deployment and configuration to meet your business needs. • Run Device Diagnostic Tests • Optimize Best-in-Class Voice Quality • Allow IT managers to configure • Optimize SIP Technology • Promote Worker Productivity devices to a corporate standard • Enable PTT without the need for a • Ensure Worker Welfare • Prevent individual users from making centralized server changes UTILITY APPS BIZ PHONE WEB API SAM CLIENT The Biz Phone app is Spectralink’s The Web API app is Spectralink’s The SAM (Spectralink Application SIP telephony application for Versity application to interface via xml Management) Client app is devices. push/pull notifications with external Spectralink’s application that services. enables Versity devices to connect • Uses Wi-Fi telephony through the with the SAM server. The SAM wireless LAN • Enable/disable API function by server is responsible for configuring • Integrates with call servers individual device, group or enterprise Spectralink applications. The SAM • Manages calls via: Multiple active • Supports JSON and XML Client app communicates heartbeat calls, transfer, forward, conference • Customize polling, pushes and information to the SAM server. calls, do not disturb, voicemail and events • Set SAM server location more • Prioritize messages • Enter SAM Account Key for user • Provides