Trigonometric Functions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Refresher Course Content
Calculus I Refresher Course Content 4. Exponential and Logarithmic Functions Section 4.1: Exponential Functions Section 4.2: Logarithmic Functions Section 4.3: Properties of Logarithms Section 4.4: Exponential and Logarithmic Equations Section 4.5: Exponential Growth and Decay; Modeling Data 5. Trigonometric Functions Section 5.1: Angles and Radian Measure Section 5.2: Right Triangle Trigonometry Section 5.3: Trigonometric Functions of Any Angle Section 5.4: Trigonometric Functions of Real Numbers; Periodic Functions Section 5.5: Graphs of Sine and Cosine Functions Section 5.6: Graphs of Other Trigonometric Functions Section 5.7: Inverse Trigonometric Functions Section 5.8: Applications of Trigonometric Functions 6. Analytic Trigonometry Section 6.1: Verifying Trigonometric Identities Section 6.2: Sum and Difference Formulas Section 6.3: Double-Angle, Power-Reducing, and Half-Angle Formulas Section 6.4: Product-to-Sum and Sum-to-Product Formulas Section 6.5: Trigonometric Equations 7. Additional Topics in Trigonometry Section 7.1: The Law of Sines Section 7.2: The Law of Cosines Section 7.3: Polar Coordinates Section 7.4: Graphs of Polar Equations Section 7.5: Complex Numbers in Polar Form; DeMoivre’s Theorem Section 7.6: Vectors Section 7.7: The Dot Product 8. Systems of Equations and Inequalities (partially included) Section 8.1: Systems of Linear Equations in Two Variables Section 8.2: Systems of Linear Equations in Three Variables Section 8.3: Partial Fractions Section 8.4: Systems of Nonlinear Equations in Two Variables Section 8.5: Systems of Inequalities Section 8.6: Linear Programming 10. Conic Sections and Analytic Geometry (partially included) Section 10.1: The Ellipse Section 10.2: The Hyperbola Section 10.3: The Parabola Section 10.4: Rotation of Axes Section 10.5: Parametric Equations Section 10.6: Conic Sections in Polar Coordinates 11. -
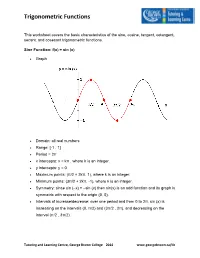
Trigonometric Functions
Trigonometric Functions This worksheet covers the basic characteristics of the sine, cosine, tangent, cotangent, secant, and cosecant trigonometric functions. Sine Function: f(x) = sin (x) • Graph • Domain: all real numbers • Range: [-1 , 1] • Period = 2π • x intercepts: x = kπ , where k is an integer. • y intercepts: y = 0 • Maximum points: (π/2 + 2kπ, 1), where k is an integer. • Minimum points: (3π/2 + 2kπ, -1), where k is an integer. • Symmetry: since sin (–x) = –sin (x) then sin(x) is an odd function and its graph is symmetric with respect to the origin (0, 0). • Intervals of increase/decrease: over one period and from 0 to 2π, sin (x) is increasing on the intervals (0, π/2) and (3π/2 , 2π), and decreasing on the interval (π/2 , 3π/2). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Cosine Function: f(x) = cos (x) • Graph • Domain: all real numbers • Range: [–1 , 1] • Period = 2π • x intercepts: x = π/2 + k π , where k is an integer. • y intercepts: y = 1 • Maximum points: (2 k π , 1) , where k is an integer. • Minimum points: (π + 2 k π , –1) , where k is an integer. • Symmetry: since cos(–x) = cos(x) then cos (x) is an even function and its graph is symmetric with respect to the y axis. • Intervals of increase/decrease: over one period and from 0 to 2π, cos (x) is decreasing on (0 , π) increasing on (π , 2π). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Tangent Function : f(x) = tan (x) • Graph • Domain: all real numbers except π/2 + k π, k is an integer. -

Lecture 5: Complex Logarithm and Trigonometric Functions
LECTURE 5: COMPLEX LOGARITHM AND TRIGONOMETRIC FUNCTIONS Let C∗ = C \{0}. Recall that exp : C → C∗ is surjective (onto), that is, given w ∈ C∗ with w = ρ(cos φ + i sin φ), ρ = |w|, φ = Arg w we have ez = w where z = ln ρ + iφ (ln stands for the real log) Since exponential is not injective (one one) it does not make sense to talk about the inverse of this function. However, we also know that exp : H → C∗ is bijective. So, what is the inverse of this function? Well, that is the logarithm. We start with a general definition Definition 1. For z ∈ C∗ we define log z = ln |z| + i argz. Here ln |z| stands for the real logarithm of |z|. Since argz = Argz + 2kπ, k ∈ Z it follows that log z is not well defined as a function (it is multivalued), which is something we find difficult to handle. It is time for another definition. Definition 2. For z ∈ C∗ the principal value of the logarithm is defined as Log z = ln |z| + i Argz. Thus the connection between the two definitions is Log z + 2kπ = log z for some k ∈ Z. Also note that Log : C∗ → H is well defined (now it is single valued). Remark: We have the following observations to make, (1) If z 6= 0 then eLog z = eln |z|+i Argz = z (What about Log (ez)?). (2) Suppose x is a positive real number then Log x = ln x + i Argx = ln x (for positive real numbers we do not get anything new). -

An Appreciation of Euler's Formula
Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 1 Article 17 An Appreciation of Euler's Formula Caleb Larson North Dakota State University Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Larson, Caleb (2017) "An Appreciation of Euler's Formula," Rose-Hulman Undergraduate Mathematics Journal: Vol. 18 : Iss. 1 , Article 17. Available at: https://scholar.rose-hulman.edu/rhumj/vol18/iss1/17 Rose- Hulman Undergraduate Mathematics Journal an appreciation of euler's formula Caleb Larson a Volume 18, No. 1, Spring 2017 Sponsored by Rose-Hulman Institute of Technology Department of Mathematics Terre Haute, IN 47803 [email protected] a scholar.rose-hulman.edu/rhumj North Dakota State University Rose-Hulman Undergraduate Mathematics Journal Volume 18, No. 1, Spring 2017 an appreciation of euler's formula Caleb Larson Abstract. For many mathematicians, a certain characteristic about an area of mathematics will lure him/her to study that area further. That characteristic might be an interesting conclusion, an intricate implication, or an appreciation of the impact that the area has upon mathematics. The particular area that we will be exploring is Euler's Formula, eix = cos x + i sin x, and as a result, Euler's Identity, eiπ + 1 = 0. Throughout this paper, we will develop an appreciation for Euler's Formula as it combines the seemingly unrelated exponential functions, imaginary numbers, and trigonometric functions into a single formula. To appreciate and further understand Euler's Formula, we will give attention to the individual aspects of the formula, and develop the necessary tools to prove it. -

Lesson 6: Trigonometric Identities
1. Introduction An identity is an equality relationship between two mathematical expressions. For example, in basic algebra students are expected to master various algbriac factoring identities such as a2 − b2 =(a − b)(a + b)or a3 + b3 =(a + b)(a2 − ab + b2): Identities such as these are used to simplifly algebriac expressions and to solve alge- a3 + b3 briac equations. For example, using the third identity above, the expression a + b simpliflies to a2 − ab + b2: The first identiy verifies that the equation (a2 − b2)=0is true precisely when a = b: The formulas or trigonometric identities introduced in this lesson constitute an integral part of the study and applications of trigonometry. Such identities can be used to simplifly complicated trigonometric expressions. This lesson contains several examples and exercises to demonstrate this type of procedure. Trigonometric identities can also used solve trigonometric equations. Equations of this type are introduced in this lesson and examined in more detail in Lesson 7. For student’s convenience, the identities presented in this lesson are sumarized in Appendix A 2. The Elementary Identities Let (x; y) be the point on the unit circle centered at (0; 0) that determines the angle t rad : Recall that the definitions of the trigonometric functions for this angle are sin t = y tan t = y sec t = 1 x y : cos t = x cot t = x csc t = 1 y x These definitions readily establish the first of the elementary or fundamental identities given in the table below. For obvious reasons these are often referred to as the reciprocal and quotient identities. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Derivation of Sum and Difference Identities for Sine and Cosine
Derivation of sum and difference identities for sine and cosine John Kerl January 2, 2012 The authors of your trigonometry textbook give a geometric derivation of the sum and difference identities for sine and cosine. I find this argument unwieldy | I don't expect you to remember it; in fact, I don't remember it. There's a standard algebraic derivation which is far simpler. The only catch is that you need to use complex arithmetic, which we don't cover in Math 111. Nonetheless, I will present the derivation so that you will have seen how simple the truth can be, and so that you may come to understand it after you've had a few more math courses. And in fact, all you need are the following facts: • Complex numbers are of the form a+bi, where a and b are real numbers and i is defined to be a square root of −1. That is, i2 = −1. (Of course, (−i)2 = −1 as well, so −i is the other square root of −1.) • The number a is called the real part of a + bi; the number b is called the imaginary part of a + bi. All the real numbers you're used to working with are already complex numbers | they simply have zero imaginary part. • To add or subtract complex numbers, add the corresponding real and imaginary parts. For example, 2 + 3i plus 4 + 5i is 6 + 8i. • To multiply two complex numbers a + bi and c + di, just FOIL out the product (a + bi)(c + di) and use the fact that i2 = −1. -

Complex Numbers and Functions
Complex Numbers and Functions Richard Crew January 20, 2018 This is a brief review of the basic facts of complex numbers, intended for students in my section of MAP 4305/5304. I will discuss basic facts of com- plex arithmetic, limits and derivatives of complex functions, power series and functions like the complex exponential, sine and cosine which can be defined by convergent power series. This is a preliminary version and will be added to later. 1 Complex Numbers 1.1 Arithmetic. A complex number is an expression a + bi where i2 = −1. Here the real number a is the real part of the complex number and bi is the imaginary part. If z is a complex number we write <(z) and =(z) for the real and imaginary parts respectively. Two complex numbers are equal if and only if their real and imaginary parts are equal. In particular a + bi = 0 only when a = b = 0. The set of complex numbers is denoted by C. Complex numbers are added, subtracted and multiplied according to the usual rules of algebra: (a + bi) + (c + di) = (a + c) + (b + di) (1.1) (a + bi) − (c + di) = (a − c) + (b − di) (1.2) (a + bi)(c + di) = (ac − bd) + (ad + bc)i (1.3) (note how i2 = −1 has been used in the last equation). Division performed by rationalizing the denominator: a + bi (a + bi)(c − di) (ac − bd) + (bc − ad)i = = (1.4) c + di (c + di)(c − di) c2 + d2 Note that denominator only vanishes if c + di = 0, so that a complex number can be divided by any nonzero complex number. -

Using Differentials to Differentiate Trigonometric and Exponential Functions Tevian Dray
Using Differentials to Differentiate Trigonometric and Exponential Functions Tevian Dray Tevian Dray ([email protected]) received his B.S. in mathematics from MIT in 1976, his Ph.D. in mathematics from Berkeley in 1981, spent several years as a physics postdoc, and is now a professor of mathematics at Oregon State University. A Fellow of the American Physical Society for his early work in general relativity, his current research interests include the octonions as well as science education. He directs the Vector Calculus Bridge Project. (http://www.math.oregonstate.edu/bridge) Differentiating a polynomial is easy. To differentiate u2 with respect to u, start by computing d.u2/ D .u C du/2 − u2 D 2u du C du2; and then dropping the last term, an operation that can be justified in terms of limits. Differential notation, in general, can be regarded as a shorthand for a formal limit argument. Still more informally, one can argue that du is small compared to u, so that the last term can be ignored at the level of approximation needed. After dropping du2 and dividing by du, one obtains the derivative, namely d.u2/=du D 2u. Even if one regards this process as merely a heuristic procedure, it is a good one, as it always gives the correct answer for a polynomial. (Physicists are particularly good at knowing what approximations are appropriate in a given physical context. A physicist might describe du as being much smaller than the scale imposed by the physical situation, but not so small that quantum mechanics matters.) However, this procedure does not suffice for trigonometric functions. -

Inverse Trig Functions Summary
Inverse trigonometric functions 1 1 z = sec ϑ The inverse sine function. The sine function restricted to [ π, π ] is one-to-one, and its inverse on this 3 − 2 2 ϑ = π ϑ = arcsec z interval is called the arcsine (arcsin) function. The domain of arcsin is [ 1, 1] and the range of arcsin is 2 1 1 1 −1 [ π, π ]. Below is a graph of y = sin ϑ, with the the part over [ π, π ] emphasized, and the graph − 2 2 − 2 2 of ϑ y. π 1 = arcsin ϑ = 2 π y = sin ϑ ϑ = arcsin y 1 π π 2 π − 1 ϑ 1 1 z − 1 π 1 π ϑ 1 1 y − 2 2 − 1 − 1 1 3 π ϑ = 2 π ϑ = 2 π − 2 By definition, By definition, 1 1 1 3 ϑ = arcsin y means that sin ϑ = y and π 6 ϑ 6 π. ϑ = arcsec z means that sec ϑ = t and 0 6 ϑ< 2 π or π 6 ϑ< 2 π. − 2 2 Differentiating the equation on the right implicitly with respect to y, gives Again, differentiating the equation on the right implicitly with respect to z, and using the restriction in ϑ, dϑ dϑ 1 1 1 one computes the derivative cos ϑ = 1, or = , provided π<ϑ< π. dy dy cos ϑ − 2 2 d 1 (arcsec z)= 2 , for z > 1. 1 1 2 2 dz z√z 1 | | Since cos ϑ> 0 on ( 2 π, 2 π ), it follows that cos ϑ = p1 sin ϑ = p1 y . -

Leonhard Euler - Wikipedia, the Free Encyclopedia Page 1 of 14
Leonhard Euler - Wikipedia, the free encyclopedia Page 1 of 14 Leonhard Euler From Wikipedia, the free encyclopedia Leonhard Euler ( German pronunciation: [l]; English Leonhard Euler approximation, "Oiler" [1] 15 April 1707 – 18 September 1783) was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function.[2] He is also renowned for his work in mechanics, fluid dynamics, optics, and astronomy. Euler spent most of his adult life in St. Petersburg, Russia, and in Berlin, Prussia. He is considered to be the preeminent mathematician of the 18th century, and one of the greatest of all time. He is also one of the most prolific mathematicians ever; his collected works fill 60–80 quarto volumes. [3] A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is our teacher in all things," which has also been translated as "Read Portrait by Emanuel Handmann 1756(?) Euler, read Euler, he is the master of us all." [4] Born 15 April 1707 Euler was featured on the sixth series of the Swiss 10- Basel, Switzerland franc banknote and on numerous Swiss, German, and Died Russian postage stamps. The asteroid 2002 Euler was 18 September 1783 (aged 76) named in his honor. He is also commemorated by the [OS: 7 September 1783] Lutheran Church on their Calendar of Saints on 24 St. Petersburg, Russia May – he was a devout Christian (and believer in Residence Prussia, Russia biblical inerrancy) who wrote apologetics and argued Switzerland [5] forcefully against the prominent atheists of his time. -

The Calculus of Trigonometric Functions the Calculus of Trigonometric Functions – a Guide for Teachers (Years 11–12)
1 Supporting Australian Mathematics Project 2 3 4 5 6 12 11 7 10 8 9 A guide for teachers – Years 11 and 12 Calculus: Module 15 The calculus of trigonometric functions The calculus of trigonometric functions – A guide for teachers (Years 11–12) Principal author: Peter Brown, University of NSW Dr Michael Evans, AMSI Associate Professor David Hunt, University of NSW Dr Daniel Mathews, Monash University Editor: Dr Jane Pitkethly, La Trobe University Illustrations and web design: Catherine Tan, Michael Shaw Full bibliographic details are available from Education Services Australia. Published by Education Services Australia PO Box 177 Carlton South Vic 3053 Australia Tel: (03) 9207 9600 Fax: (03) 9910 9800 Email: [email protected] Website: www.esa.edu.au © 2013 Education Services Australia Ltd, except where indicated otherwise. You may copy, distribute and adapt this material free of charge for non-commercial educational purposes, provided you retain all copyright notices and acknowledgements. This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations. Supporting Australian Mathematics Project Australian Mathematical Sciences Institute Building 161 The University of Melbourne VIC 3010 Email: [email protected] Website: www.amsi.org.au Assumed knowledge ..................................... 4 Motivation ........................................... 4 Content ............................................. 5 Review of radian measure ................................. 5 An important limit ....................................