Unlocking Amenities: Estimating Public Good Complementarity
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Unit 4. Consumer Behavior
UNIT 4. CONSUMER BEHAVIOR J. Alberto Molina – J. I. Giménez Nadal UNIT 4. CONSUMER BEHAVIOR 4.1 Consumer equilibrium (Pindyck → 3.3, 3.5 and T.4) Graphical analysis. Analytical solution. 4.2 Individual demand function (Pindyck → 4.1) Derivation of the individual Marshallian demand Properties of the individual Marshallian demand 4.3 Individual demand curves and Engel curves (Pindyck → 4.1) Ordinary demand curves Crossed demand curves Engel curves 4.4 Price and income elasticities (Pindyck → 2.4, 4.1 and 4.3) Price elasticity of demand Crossed price elasticity Income elasticity 4.5 Classification of goods and demands (Pindyck → 2.4, 4.1 and 4.3) APPENDIX: Relation between expenditure and elasticities Unit 4 – Pg. 1 4.1 Consumer equilibrium Consumer equilibrium: • We proceed to analyze how the consumer chooses the quantity to buy of each good or service (market basket), given his/her: – Preferences – Budget constraint • We shall assume that the decision is made rationally: Select the quantities of goods to purchase in order to maximize the satisfaction from consumption given the available budget • We shall conclude that this market basket maximizes the utility function: – The chosen market basket must be the preferred combination of goods or services from all the available baskets and, particularly, – It is on the budget line since we do not consider the possibility of saving money for future consumption and due to the non‐satiation axiom Unit 4 – Pg. 2 4.1 Consumer equilibrium Graphical analysis • The equilibrium is the point where an indifference curve intersects the budget line, with this being the upper frontier of the budget set, which gives the highest utility, that is to say, where the indifference curve is tangent to the budget line q2 * q2 U3 U2 U1 * q1 q1 Unit 4 – Pg. -

Evidence from a Laboratory Experiment on Impure Public Goods
MPRA Munich Personal RePEc Archive Green goods: are they good or bad news for the environment? Evidence from a laboratory experiment on impure public goods Munro, Alistair and Valente, Marieta National Graduate Institute for Policy Studies, Tokyo, Japan, NIMA { Applied Microeconomics Research Unit, University of Minho, Portugal, Department of Economics, Royal Holloway University of London, UK 30. October 2008 Online at http://mpra.ub.uni-muenchen.de/13024/ MPRA Paper No. 13024, posted 27. January 2009 / 03:02 Green goods: are they good or bad news for the environment? Evidence from a laboratory experiment on impure public goods (Version January-2009) Alistair Munro Department of Economics, Royal Holloway University of London, UK National Graduate Institute for Policy Studies Tokyo, Japan and Marieta Valente (corresponding author: email to [email protected] ) Department of Economics, Royal Holloway University of London, UK NIMA – Applied Microeconomics Research Unit, University of Minho, Portugal The authors thank Dirk Engelmann for helpful comments and suggestions as well as participants at the Research Strategy Seminar at RHUL 2007, IMEBE 2008, Experimental Economics Days 2008 in Dijon, EAERE 2008 meeting, European ESA 2008 meeting. Also, we thank Claire Blackman for her help in recruiting subjects. Marieta Valente acknowledges the financial support of Fundação para a Ciência e a Tecnologia. Abstract An impure public good is a commodity that combines public and private characteristics in fixed proportions. Green goods such as dolphin-friendly tuna or green electricity programs provide increasings popular examples of impure goods. We design an experiment to test how the presence of impure public goods affects pro-social behaviour. -

Mathematical Economics
Mathematical Economics Dr Wioletta Nowak, room 205 C [email protected] http://prawo.uni.wroc.pl/user/12141/students-resources Syllabus Mathematical Theory of Demand Utility Maximization Problem Expenditure Minimization Problem Mathematical Theory of Production Profit Maximization Problem Cost Minimization Problem General Equilibrium Theory Neoclassical Growth Models Models of Endogenous Growth Theory Dynamic Optimization Syllabus Mathematical Theory of Demand • Budget Constraint • Consumer Preferences • Utility Function • Utility Maximization Problem • Optimal Choice • Properties of Demand Function • Indirect Utility Function and its Properties • Roy’s Identity Syllabus Mathematical Theory of Demand • Expenditure Minimization Problem • Expenditure Function and its Properties • Shephard's Lemma • Properties of Hicksian Demand Function • The Compensated Law of Demand • Relationship between Utility Maximization and Expenditure Minimization Problem Syllabus Mathematical Theory of Production • Production Functions and Their Properties • Perfectly Competitive Firms • Profit Function and Profit Maximization Problem • Properties of Input Demand and Output Supply Syllabus Mathematical Theory of Production • Cost Minimization Problem • Definition and Properties of Conditional Factor Demand and Cost Function • Profit Maximization with Cost Function • Long and Short Run Equilibrium • Total Costs, Average Costs, Marginal Costs, Long-run Costs, Short-run Costs, Cost Curves, Long-run and Short-run Cost Curves Syllabus Mathematical Theory of Production Monopoly Oligopoly • Cournot Equilibrium • Quantity Leadership – Slackelberg Model Syllabus General Equilibrium Theory • Exchange • Market Equilibrium Syllabus Neoclassical Growth Model • The Solow Growth Model • Introduction to Dynamic Optimization • The Ramsey-Cass-Koopmans Growth Model Models of Endogenous Growth Theory Convergence to the Balance Growth Path Recommended Reading • Chiang A.C., Wainwright K., Fundamental Methods of Mathematical Economics, McGraw-Hill/Irwin, Boston, Mass., (4th edition) 2005. -

IS EFFICIENCY BIASED? Zachary Liscow* August 2017 ABSTRACT: the Most Common Underpinning of Economic Analysis of the Law Has
IS EFFICIENCY BIASED? Zachary Liscow* August 2017 ABSTRACT: The most common underpinning of economic analysis of the law has long been the goal of efficiency (i.e., choosing policies that maximize people’s willingness to pay), as reflected in economic analysis of administrative rulemaking, judicial rules, and proposed legislation. Current thinking is divided on the question whether efficient policies are biased against the poor, which is remarkable given the question’s fundamental nature. Some say yes; others, no. I show that both views are supportable and that the correct answer depends upon the political and economic context and upon the definition of neutrality. Across policies, efficiency-oriented analysis places a strong thumb on the scale in favor of distributing more legal entitlements to the rich than to the poor. Basing analysis on willingness to pay tilts policies toward benefitting the rich over the poor, since the rich tend to be willing to pay more due to their greater resources. But I also categorize different types of polices and show where vigilance against anti-poor bias is warranted and where it is not, with potentially far-reaching implications for the policies that judges, policymakers, and voters should support. Table of Contents Introduction ................................................................................................................. 2 I. Social Welfare ..................................................................................................... 7 II. Efficiency ......................................................................................................... -

1. Consider the Following Preferences Over Three Goods: �~� �~� �~� � ≽ �
1. Consider the following preferences over three goods: �~� �~� �~� � ≽ � a. Are these preferences complete? Yes, we have relationship defined between x and y, y and z, and x and z. b. Are these preferences transitive? Yes, if �~� then � ≽ �. If �~� then � ≽ �. If �~� then �~� and � ≽ �. Thus the preferences are transitive. c. Are these preferences reflexive? No, we would need � ≽ � � ≽ � 2. Write a series of preference relations over x, y, and z that are reflexive and complete, but not transitive. � ≽ � � ≽ � � ≽ � � ≽ � � ≽ � � ≻ � We know this is not transitive if � ≽ � and � ≽ � then � ≽ �. But � ≻ �, which would contradict transitivity. 3. Illustrate graphically a set of indifference curves where x is a neutral good and y is a good that the person likes: We know that this person finds x to be a neutral good because adding more x while keeping y constant (such as moving from bundle A to D, or from B to E), the person is indifferent between the new bundle with more x and the old bundle with less x. We know this person likes y because adding more y while keeping x constant (such as moving from bundle A to B, or from D to E), the person is strictly prefers the new bundle with more y than the old bundle with less y. 4. Draw the contour map for a set of preferences when x and y are perfect substitutes. Are these well-behaved? Explain why or why not. We know these are perfect substitutes because they are linear (the MRS is constant) We know they are strictly monotonic because adding Y while keeping X constant (moving from bundle A to bundle B), leads to a strictly preferred bundle (� ≻ �). -

Chapter 4 Individual and Market Demand
Chapter 4: Individual and Market Demand CHAPTER 4 INDIVIDUAL AND MARKET DEMAND EXERCISES 1. The ACME corporation determines that at current prices the demand for its computer chips has a price elasticity of -2 in the short run, while the price elasticity for its disk drives is -1. a. If the corporation decides to raise the price of both products by 10 percent, what will happen to its sales? To its sales revenue? We know the formula for the elasticity of demand is: %DQ E = . P %DP For computer chips, EP = -2, so a 10 percent increase in price will reduce the quantity sold by 20 percent. For disk drives, EP = -1, so a 10 percent increase in price will reduce sales by 10 percent. Sales revenue is equal to price times quantity sold. Let TR1 = P1Q1 be revenue before the price change and TR2 = P2Q2 be revenue after the price change. For computer chips: DTRcc = P2Q2 - P1Q1 DTRcc = (1.1P1 )(0.8Q1 ) - P1Q1 = -0.12P1Q1, or a 12 percent decline. For disk drives: DTRdd = P2Q2 - P1Q1 DTRdd = (1.1P1 )(0.9Q1 ) - P1Q1 = -0.01P1Q1, or a 1 percent decline. Therefore, sales revenue from computer chips decreases substantially, -12 percent, while the sales revenue from disk drives is almost unchanged, -1 percent. Note that at the point on the demand curve where demand is unit elastic, total revenue is maximized. b. Can you tell from the available information which product will generate the most revenue for the firm? If yes, why? If not, what additional information would you need? No. -

Chapter 3—Supply and Demand: Theory
Chapter 3—Supply and Demand: Theory MULTIPLE CHOICE 1. The law of demand states that price and quantity demanded are a. directly related, ceteris paribus. b. inversely related, ceteris paribus. c. independent. d. positively related, ceteris paribus. ANS: B PTS: 1 DIF: Difficulty: Easy NAT: BUSPROG: Analytic LOC: DISC: Supply and demand KEY: Bloom's: Knowledge 2. Which of the following illustrates the law of demand? a. Jorge buys fewer pencils at $2 per pencil than at $1 per pencil, ceteris paribus. b. Chen buys more ice cream at $4 per half-gallon than at $3 per half gallon, ceteris paribus. c. Karissa buys fewer sweaters at $50 each than at $35 each, ceteris paribus. d. a, b, and c e. a and c ANS: E PTS: 1 DIF: Difficulty: Moderate NAT: BUSPROG: Analytic LOC: DISC: Supply and demand KEY: Bloom's: Application 3. At a price of $15 each, Marta buys 4 books per month. When the price increases to $20, Marta buys 3 books per month. Luz says that Marta's demand for books has decreased. Is Luz correct? a. Yes, Luz is correct. b. No, Luz is incorrect. Marta's demand has increased. c. No, Luz is incorrect. Marta's quantity demanded has decreased, but her demand has stayed the same. d. No, Luz is incorrect. Marta's quantity demanded has increased, but her demand has stayed the same. e. No, Luz is incorrect. Marta's quantity demanded has decreased and her demand has increased. ANS: C PTS: 1 DIF: Difficulty: Challenging NAT: BUSPROG: Analytic LOC: DISC: Supply and demand KEY: Bloom's: Application 4. -

An Analysis of the Supply of Open Government Data
future internet Article An Analysis of the Supply of Open Government Data Alan Ponce 1,* and Raul Alberto Ponce Rodriguez 2 1 Institute of Engineering and Technology, Autonomous University of Cd Juarez (UACJ), Cd Juárez 32315, Mexico 2 Institute of Social Sciences and Administration, Autonomous University of Cd Juarez (UACJ), Cd Juárez 32315, Mexico; [email protected] * Correspondence: [email protected] Received: 17 September 2020; Accepted: 26 October 2020; Published: 29 October 2020 Abstract: An index of the release of open government data, published in 2016 by the Open Knowledge Foundation, shows that there is significant variability in the country’s supply of this public good. What explains these cross-country differences? Adopting an interdisciplinary approach based on data science and economic theory, we developed the following research workflow. First, we gather, clean, and merge different datasets released by institutions such as the Open Knowledge Foundation, World Bank, United Nations, World Economic Forum, Transparency International, Economist Intelligence Unit, and International Telecommunication Union. Then, we conduct feature extraction and variable selection founded on economic domain knowledge. Next, we perform several linear regression models, testing whether cross-country differences in the supply of open government data can be explained by differences in the country’s economic, social, and institutional structures. Our analysis provides evidence that the country’s civil liberties, government transparency, quality of democracy, efficiency of government intervention, economies of scale in the provision of public goods, and the size of the economy are statistically significant to explain the cross-country differences in the supply of open government data. Our analysis also suggests that political participation, sociodemographic characteristics, and demographic and global income distribution dummies do not help to explain the country’s supply of open government data. -

Unlocking Amenities: Estimating Public Good Complementarity
Unlocking Amenities: Estimating Public Good Complementarity June 9, 2018 Abstract Research on public goods generally considers the value of individual public goods in isolation, when in fact there may be strong complementarities between them. This study examines the implications of public goods complementarities for economic val- uation and efficient public investment, using the setting of public safety and open space in inner cities. Cross-sectional, difference-in-difference, and instrumental- variable estimates from Chicago, New York, and Philadelphia all indicate that local crime lowers the amenity value of public parks to nearby residents. Public safety improvements \unlock" the value of open-space amenities, and could raise the value that properties receive from adjacent parks from $22 billion to $31 billion in those three cities. Ignoring these complementarities risks over-estimating benefits in dangerous areas, under-estimating benefits in poor areas or conflating reduced amenity value with the preferences of local populations, and under-estimating ben- efits overall. While safety is more fundamental in a hierarchy of amenities, open spaces are not a luxury. Key words: public goods, complements, amenities, crime, environmental amenities, parks, urban development JEL Classification: H41, Q51, Q56 1 Introduction Economic theory leans heavily on the concept that goods may be complements in con- sumption. While the joint demand of private goods, purchased directly in markets, has been studied extensively, little has been said on the joint demand for public goods. Study- ing the joint demand for public goods is difficult since they cannot be purchased directly, but only indirectly, such as access through the housing market.1 To our knowledge, no prior study has priced relationships between public goods in a well-identified causal frame- work. -
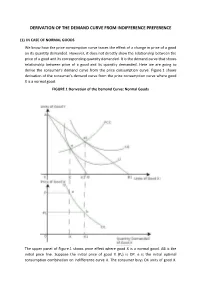
Derivation of the Demand Curve from Indifference Preference
DERIVATION OF THE DEMAND CURVE FROM INDIFFERENCE PREFERENCE (1) IN CASE OF NORMAL GOODS We know how the price consumption curve traces the effect of a change in price of a good on its quantity demanded. However, it does not directly show the relationship between the price of a good and its corresponding quantity demanded. It is the demand curve that shows relationship between price of a good and its quantity demanded. Here we are going to derive the consumer's demand curve from the price consumption curve. Figure.1 shows derivation of the consumer's demand curve from the price consumption curve where good X is a normal good. FIGURE.1 Derivation of the Demand Curve: Normal Goods The upper panel of Figure.1 shows price effect where good X is a normal good. AB is the initial price line. Suppose the initial price of good X (Px) is OP. e is the initial optimal consumption combination on indifference curve U. The consumer buys OX units of good X. When price of X (Px)falls, to say OP1, the budget constraint shift to AB1. The optimal consumption combination is e1 on indifference curve U1. The consumer now increases consumption of good X from OX to OX1 units. The Price Consumption Curve (PCC) is rising upwards. Chart.1 shows the demand relationship derived form the price consumption curve. The lower panel of Figure.1 shows this price and corresponding quantity demanded of good X as shown in Chart.1. At initial price OP, quantity demanded of good X is OX. -

Study Plan Economics
STUDY PLAN ECONOMICS EduSure School Economics PG Entrance Course Study Plan for Eco Topper Course-1 Year Prep Learning under: Ankit & Mahima Banthia Macro-economics Select Subject: Macro/Devt/Trade Eco Topper [MacroET] @ elearn.edusure.in to access the course content for macroeconomics This subject contains the following chapters Chapter 1 + Simple Keynesian Model Chapter 2 + IS-LM Model Chapter 3 + Open Economy ISLM Chapter 4 + AD AS Model Chapter 5 + Growth Models Chapter 6 + Development Economics Chapter 7 + International Trade Chapter 8 + National Income Accounting Chapter 9 + Money and other extra notes Chapter 10 + Mock Test Discussion 2019 - look at individual subjects to find more videos there Chapter 11 + last jnu videos Chapter 12 + latest JNU answers 1. Chapters 1-8 contain Course Material, Practice Questions, 15 years video solutions to past papers for Macroeconomics, Trade and Development Economics 2. Chapter 9 holds extra notes for various small topics across all economics. Under heading Xtra for subject Macro/Devt/Trade Eco Topper • Here you will find all the practice problems of all Macroeconomics uploaded by EduSure Under heading Forum for subject Macroeconomics Eco Topper [MacroET] • Here you can post doubts, questions for your friends and us to answer. Under heading Study Material for subject Macro/Devt/Trade Eco Topper I. Simple Keynesian Model • See Theory Video – No.s 2,3,5-9 under SKM • Look at EduSure SKM Note “Theory - Notes and Questions”: Subtopic No. 1 • Read topic Keynesian Cross from the book Mankiw STUDY PLAN ECONOMICS • Solve all past paper questions given in SKM handout • Look at video solutions to past paper questions under subtopics 9-62 • Solve the relevant practice problems given under Xtra • II. -

Is Efficiency Biased? Zachary Liscow†
Is Efficiency Biased? Zachary Liscow† Efficiency is a watchword in policy circles. If we choose policies that maximize people’s willingness to pay, we are told, we will grow the economic pie and thus benefit the rich and poor alike. Who would oppose efficiency when it is cast in this fashion? However, there are actually two starkly different types of efficient policies: those that systematically distribute equally to the rich and the poor and those that system- atically distribute more to the rich. Our collective failure to grasp this distinction matters enormously for those with a wide range of political commitments. Many efficient policies distribute more to the rich without the rich having to pay for their bigger slice. Because these “rich- biased” policies are ubiquitous, efficient policymaking places a heavy thumb on the scale in favor of the rich. Especially at this time of heightened concern about inequality, getting efficiency right should matter to a wide swath of the policymaking spectrum, from committed redistributionists to libertarians. We should support efficient policies only when the poor are compensated for their smaller slices or when efficient policies systematically distribute equally to the rich and the poor as we grow the size of the economic pie. This Article points a way forward in ensuring that a foundational tenet of the law does not follow a “rich get richer” principle, with profound consequences for policymaking. INTRODUCTION ................................................................................................... 1650 I. EFFICIENCY: AN EXPLANATION ................................................................... 1658 II. THE DISTRIBUTIONAL CONSEQUENCES OF POLICIES: A STICKY TAKE ......... 1662 III. LEGAL ENTITLEMENT NEUTRALITY ............................................................. 1667 A. Neutral Policies ................................................................................. 1669 † Associate Professor, Yale Law School.