DOCSLIB.ORG

Junior Mathematics Competition 2018 Solutions and Comments

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Junior Mathematics Competition 2018 Solutions and Comments Department of Mathematics and Statistics Junior Mathematics Competition 2018 Solutions and Comments Web: maths.otago.ac.nz/jmc Twitter: @uojmc YEAR 9 (FORM 3) PRIZE WINNERS FIRST GrACE WU ST CUTHBERT’S COLLEGE SECOND JAMES (He) XU KRISTIN SCHOOL THIRD MICHAEL Li MACLEANS COLLEGE TOP 30 (IN SCHOOL ORDER): DaVID EVANs, CANTERBURY HOME EDUCATORS HAMISH KERR, HAMILTON BOYS’ HIGH SCHOOL SAMUEL DaRR, HUTT INTERMEDIATE SCHOOL RHIANNON MACKIe, HUTT VALLEY HIGH SCHOOL MARTIN BROOK, JOHN MCGlASHAN COLLEGE RANITHU SENDIV RODRIGo, JOHN PaUL COLLEGE WESLEY NGo, KINGS COLLEGE ANDREW YU, KINGS COLLEGE CATHERINE ZHANG, LyNଏELD COLLEGE KEVIN LiN, MACLEANS COLLEGE WEI TIAN Teo, MACLEANS COLLEGE HOSEA TONG-Ho, MACLEANS COLLEGE REGINA YUN, MACLEANS COLLEGE NANCY CHEN, MACLEANS COLLEGE JESSICA HONG, MACLEANS COLLEGE JAMES HUI, MACLEANS COLLEGE KERWIN MAAss, NEWLANDS COLLEGE ZIYUE (CLAIRe) XU, NORTHCROSS INTERMEDIATE HENRY ZASLOW, ONSLOW COLLEGE LuCY AITKEN, RANGI RURU GiRLS’ SCHOOL JESSICA WANG, RANGITOTO COLLEGE GrACE PuI, ST CUTHBERT’S COLLEGE EMMA YiNG, ST CUTHBERT’S COLLEGE BRENA MERZ, ST CUTHBERT’S COLLEGE BRADEN Dye, ST KENTIGERN COLLEGE MAX FENG, ST KENTIGERN COLLEGE TONY SHI, WESTLAKE BOYs’ HIGH SCHOOL YEAR 10 (FORM 4) PRIZE WINNERS FIRST MICHAEL KENNEDY LiSTON COLLEGE SECOND OLIVER DaI MACLEANS COLLEGE THIRD JAMES SUTTON RONGOTAI COLLEGE TOP 30 (IN SCHOOL ORDER): ALDOUS SCHOLLUM, AVONDALE COLLEGE SHREYA SRIRAM, AVONDALE COLLEGE DuNCAN HAMILTON, CHRISTCHURCH BOYS’ HIGH SCHOOL HARRY NEIL, HILLCREST HIGH SCHOOL TOBIAS DeVEREUX, KAVANAGH COLLEGE JASON Lee, KINGS COLLEGE ERIC ZHANG, KRISTIN SCHOOL ANNIE PenG, KRISTIN SCHOOL MAGGIE CHEN, MACLEANS COLLEGE RICK HAN, MACLEANS COLLEGE LiSA SANDBROOK, MACLEANS COLLEGE JEREMY HUANG, MACLEANS COLLEGE ANNA Li, OREWA COLLEGE OLIVER LiN, PaKURANGA COLLEGE KIKI SU, PaKURANGA COLLEGE SEOHYUN KIM, RANGITOTO COLLEGE TONY SCHAUFELBERGER, RUTHERFORD COLLEGE JET SHAND-Pease, SELWYN COLLEGE ARISA MORI, ST ANDREW’S COLLEGE JENNY YUAN, ST CUTHBERT’S COLLEGE JUSTIN XIANG, ST KENTIGERN COLLEGE NATHAN XU, ST KENTIGERN COLLEGE MICHELLE GuAN, ST KENTIGERN COLLEGE EVAN METCALFe, ST KENTIGERN COLLEGE HAOKUN He, ST KENTIGERN COLLEGE PhILLIP HAN, WESTLAKE BOYs’ HIGH SCHOOL TAEWON YUN, WESTLAKE BOYS’ HIGH SCHOOL YEAR 11 (FORM 5) PRIZE WINNERS FIRST EQUAL LuKE YING FENG BAO AUCKLAND GrAMMAR SCHOOL FIRST EQUAL CHEN HUAN LiU EPSOM GiRLS’ GrAMMAR SCHOOL THIRD TERRY SHEN MACLEANS COLLEGE TOP 30 (IN SCHOOL ORDER): ANDREW JIA AN CHe, AUCKLAND GrAMMAR SCHOOL NATHAN CHEN, AUCKLAND GrAMMAR SCHOOL MACKINLEY HE, AUCKLAND GrAMMAR SCHOOL ANDREW YU AN CHEN, AUCKLAND INTERNATIONAL COLLEGE ISAAC HAo-EN YUAN, AUCKLAND INTERNATIONAL COLLEGE MAX YOUNG, CHRISTCHURCH BOYs’ HIGH SCHOOL VICTORIA SUN, EPSOM GiRLS’ GrAMMAR SCHOOL DaNIEL CLARK, GlENDOWIE COLLEGE EMILY ZOU, GlENDOWIE COLLEGE ISHAN NATH, JOHN PaUL COLLEGE NATHANIEL MASFEN-YAN, KINGS COLLEGE HANBO XIe, KINGS COLLEGE RANUDI LelWALA, MACLEANS COLLEGE JAMIE WU, MACLEANS COLLEGE YUNGE YU, MACLEANS COLLEGE ANGELA YANG, MACLEANS COLLEGE DaRSH CHAUDHARI, MACLEANS COLLEGE KELVIN Gu, MACLEANS COLLEGE RAY WU, NEWLANDS COLLEGE JEREMY ISHI, PaKURANGA COLLEGE YUHAN (LiNDA) TANG, PiNEHURST SCHOOL MINJU KIM, RANGITOTO COLLEGE XAVIER YiN, ST KENTIGERN COLLEGE TONY YU, ST KENTIGERN COLLEGE GrACE CHANG, ST KENTIGERN COLLEGE JAMES ALEXANDER, ST Peter’S COLLEGE (EPSOM) STEVEN WANG, ST Peter’S SCHOOL (CAMBRIDGe) 2018 ANSWERS AS ALWAYS ONLY ONE METHOD IS SHOWN. OFTEN SEVERAL METHODS EXISt. WE DON’T GUARANTEE THAT THE METHOD SHOWN IS THE BEST OR FASTESt. QUESTION 1: 10 MARKS (YEARS 9 AND BELOW ONLY) (A) A RECTANGULAR WALL MEASURES 4.5 M BY 3 M. SHOW THAT THE AREA OF THE WALL IS 13.5 M2. EITHER 4.5 × 3 OR 3 × 4.5. AN EASY START BUT SURPRISINGLY A FEW STUDENTS MISSED IT OUT! (B) SUPPOSE THE AREA OF A ROLL OF WALLPAPER HAS DIMENSIONS 5 M BY 0.5 M. (I) WHAT IS THE AREA COVERED BY ONE ROLL OF WALLPAPER? 5 × 0.5 = 2.5 M2. WELL DONE. (MANY STUDENTS WROTE 2.5 M INSTEAD OF 2.5 M2.) (II) HOW MANY ‘WHOLE’ ROLLS OF WALLPAPER WOULD YOU NEED TO COVER THE WALL IN PART (A)? YOUR ANSWER SHOULD NOT HAVE A FRACTION OR DECIMAL COMPONENT IN It. 13.5 / 2.5 = 5.4 SO 6 ROLLS ARE NEEDED. MANY STUDENTS ROUNDED ‘DOWN’ TO 5, LEAVING PART OF THE WALL BARE OF WALLPAPER. REMEMBER THAT IS GENERALLY BETTER TO BUY A LITTLE TOO MUCH THAN NOT ENOUGH! (C) IF A WINDOW COVERS 2.7 M2 ON THE WALL, WHAT PERCENTAGE OF THE WALL IS COVERED BY THE WINDOW? THIS WAS WELL ANSWERED IN THE MAIN. 2.7 / 13.5 × 100 = 20%. QUESTION 2: 10 MARKS (YEARS 10 AND BELOW ONLY) A STORE SELLS REFRIGERATORS WITH A RECOMMENDED PRICE OF $1600. HOWEVER THEY KNOW THAT THEY CANNOT SELL ANY AT THIS PRICE SO THEY OffER THEM AT A ‘SPECIAL’ PRICE OF $1200. (A) WHAT IS THE PERCENTAGE DISCOUNT OF $1200 COMPARED TO $1600? 1200 / 1600 = 75% SO THE ANSWER IS A 25% DISCOUNT. REASONABLE, ALTHOUGH A FEW STUDENTS DIVIDED 1600 BY 1200 AND SOME LEFT 75% AS THEIR ANSWER. (B) IN A BOXING DaY SALE THEY OffER THE FRIDGE AT A SPECIAL ‘20% SAVING’ I.e. 20% Off THE RECOMMENDED PRICE OF $1600. (I) WHAT IS THE SPECIAL BOXING DaY ‘SALE’ PRICe? $1600 - $320 = $1280. WELL ANSWERED IN THE MAIN. THE MOST COMMON MISTAKE WAS TO LEAVE $320 AS THE ଏNAL ANSWER. (II) Does THIS SALE PRICE REPRESENT A SAVING ON THE ‘SPECIAL’ PRICE OR AN INCREAse? YOU DON’T HAVE TO SHOW WORKING. IT’S AN INCREASE SINCE $1280 IS MORE THAN $1200. GENERALLY WELL ANSWERED ALTHOUGH STUDENTS WHO WROTE ‘YES’ OR ‘NO’ WEREN’T GIVING AN ANSWER AT ALL. (C) THEY OffER A ‘FURTHER 20%’ Off THE SALE PRICE IF A CUSTOMER PAYS CASH. WHAT PERCENTAGE SAVING DO THESE TWO PERCENTAGES COMBINED REPRESENt? (1 - 0.8 × 0.8) = 36%. THIS WAS THE ଏRST ‘DIଏCULT’ QUESTION. IF WE TAKE $100 AS THE NORMAL PRICE THEN A 20% DISCOUNT LEADS TO AN $80 SALE PRICE. 20% OF $80 IS $16 SO THE ଏNAL PRICE IS $64, WHICH REPRESENTS A 36% DISCOUNT. SOME STUDENTS WORKED IT OUT. GENERALLY THIS QUESTION WAS A GOOD INDICATOR AS TO WHETHER A STUDENT EVENTUALLY GAINED A MERIT (OR ABOVE) OR NOT. (D) ANOTHER STORE USUALLY MAKES 400% PROଏT ON ITEMS THEY SELL. FOR EXAMPLE AN ITEM COSTING THE STORE $20 WOULD SELL FOR $100. IN A SALE THEY OffER THE $100 ITEM FOR 50% Off THE USUAL PRICe. WHAT PERCENTAGE PROଏT ON THE ITEM DO THEY STILL MAKe? 50% OF $100 IS $50; THUS A $30 PROଏT STILL EXISTS. IF THE ORIGINAL ITEM COST THE STORE $20 THEN THEY STILL MAKE A PROଏT OF 30 / 20 = 150%. MANY STUDENTS WORKED THIS OUT, BUT IT WAS ALSO OFTEN WRONG. 250% AND 30% (OR $30) WERE NOT UNCOMMON. NON-SENSIBLE ANSWERS BIGGER THAN THE ORIGINAL 400% OCCASIONALLY APPEARED. QUESTION 3: 20 MARKS (ALL YEARS) THIS QUESTION WAS FAIRLY ‘EASY’ FOR MANY STUDENTS. FULL CREDIT WAS COMMON. (A) HARRY AND MEGHAN PLAN TO BAKE MUଏNS FOR AFTERNOON TEA. HOWEVER, THE ORIGINAL RECIPE SERVES ଏVE PEOPLe. THEY WILL HAVE TO ADJUST THE AMOUNT OF INGREDIENTS THEY NEED TO SERVE THE TWO OF THEM. (I) THE ORIGINAL RECIPE CALLS FOR 100 G OF BUTTER. HOW MUCH BUTTER IS NEEDED FOR TWO PEOPLe? 2/5 OF 100 IS 40 G. RATIO WAS WELL UNDERSTOOD. (II) THE ORIGINAL RECIPE CALLS FOR 15/16 OF A CUP OF BLUEBERRIES. WHAT FRACTION OF A CUP DO THEY NEED FOR TWO 15/16 PEOPLe? BRIEଏY SHOW YOUR WORKING. 5/2 = 3/8. THERE WERE SEVERAL CANDIDATES WHO REACHED 6/6.4 HERE. THEY SHOWED NO UNDERSTANDING OF DEALING WITH FRACTIONS. (III) HARRY AND MEGHAN WORK OUT THAT THEY NOW NEED TWO CUPS OF ଏOUR. HOW MANY CUPS OF ଏOUR DID THE ORIGINAL RECIPE CALL FOR? 5 CUPS, SINCE 2/5 OF 5 IS 2. (IV) THEY WORK OUT THAT FOR TWO PEOPLE THEY NEED HALF A CUP OF PLAIN YOGHURt. HOW MUCH PLAIN YOGHURT DID THE ORIGINAL RECIPE CALL FOR (I.e. FOR ଏVE PEOPLe)? 0.5 × 5/2 = 1.25 CUPS. A FEW STUDENTS GOT 5/4 BUT LOST CREDIT WHEN THEY GAVE THE ଏNAL ANSWER AS 1.5 CUPS. 2.5 WAS ALSO A ‘COMMON’ MISTAKE. (B) A GOOD RULE OF THUMB FOR CONVERTING OUNCES (OZ) TO GRAMS (G) (ALTHOUGH IT IS NOT PERFECT MATHEMATICALLY) IS TO USE THE FORMULA 1 OZ = 30 G. UsE THIS TO ANSWER THE FOLLOWING TRUE OR FALSE QUESTIONS (YOU DON’T NEED TO SHOW WORKING): (I) 2 G = 60 OZ. FALSE. THIS PROVED TO BE THE HARDEST PART OF THE QUESTION! SEVERAL STUDENTS DIDN’T NOTICE THAT IT WAS ‘BACK-TO-FRONT’. (II) 1.6 OZ = 48 G. TRUE. WELL ANSWERED. (III) 1 KG = 33 OZ (TO THE NEAREST WHOLE NUMBER). TRUE. (1000 / 30 = 33 TO THE NEAREST WHOLE NUMBER.) UNFOR- TUNATELY THIS QUESTION IS AMBIGUOUS AND ‘FALSE’ COULD BE GIVEN BY STUDENTS WHO ’STARTED AT THE RIGHT’. (33 30 = 990, NOT 1000.) THE TROUBLE WITH AMBIGUOUS QUESTIONS IS THAT A FEW STUDENTS ‘WASTE TIME’ ଏGURING× WHICH IS THE ANSWER WE LOOKED FOR. A FEW STUDENTS GAVE BOTH ANSWERS, WITH EXPLANATIONS. THE ANSWER SCHEDULE WAS ADJUSTED FOR THE ERROR. (C) THERE ARE 16 OUNCES (OZ) IN A POUND. REMEMBER THAT WE ARE USING THE APPROXIMATION 1 OZ = 30 G. (I) HOW MANY GRAMS ARE THERE IN 1 POUND? 30 × 16 = 480 G. ALMOST UNIVERSALLY ANSWERED CORRECTLY. (II) HOW MANY POUNDS ARE THERE IN A 6 KG OF ଏOUR? WE WERE LOOKING FOR 6000 / 30 = 200 (OUNCES) AND THEN 200 / 16 = 12.5 (POUNDS). BUT MOST STUDENTS GAVE 6000 / 480 = 12.5 WHICH WAS ଏNE. THE PROBLEM WITH USING ONE OF YOUR OWN ANSWERS IN A LATER PART OF THE QUESTION IS THAT IT MAY BE WRONG, AND SO YOUR SECOND ANSWER BECOMES ‘WRONG’ TOO.
Load more

Recommended publications
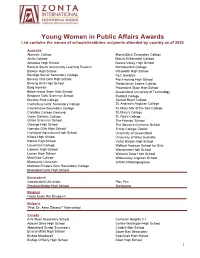
  • Young Women in Public Affairs Awards List Contains the Names of Schools/Institutes Recipients Attended by Country As of 2020
    Young Women in Public Affairs Awards List contains the names of schools/institutes recipients attended by country as of 2020 Australia Alanvale College Mount Eliza Secondary College Amity College Mount St Benedict College Armidale High School Narara Valley High School Ballarat South Community Learning Precinct Narrabundah College Balwyn High School Pittsworth High School Bendigo Senior Secondary College PLC Armidale Beverly Hills Girls High School Port Hacking High School Birrong Girls High School Presbyterian Ladies College Borg Nonntal Proserpine State High School Bribie Island State High School Queensland University of Technology Brisbane Girls Grammar School Radford College Buckley Park College Sacred Heart College Canterbury Girls' Secondary College St. Andrew's Anglican College Castlemaine Secondary College St. Mary Star of the Sea College Christian College Geelong St. Mary’s College Galen Catholic College St. Rita's College Girton Grammar School The Friends' School Glossop High School The Illawarra Grammar School Hornsby Girls High School Trinity College Gawler Hurlstone Agricultural High School University of Queensland Killara High School University of West Australia Kotara High School Victor Harbor High School Laucenton College Walford Anglican School for Girls Lismore High School Wangaratta High School Loxton High School Warwick State High School MacKillop College Whitsunday Anglican School Macquarie University GWIKU Haizingergasse Matthew Flinders Girls' Secondary College Moorefield Girls High School Bangladesh Independent
    [Show full text]
  • December 2020
    An occasional publication from Kavanagh College Message from the Principal Welcome to our end of year publication of Ipsa Duce. Whether you have been a leader in our college, one We enjoy being able to share a brief overview of some of our longest serving staff, one of our valued support of our significant highlights from the latter part of this staff and teacher aides, or a board member, maybe year. This year has been complex. People have found a supporter of Kavanagh College from the wider different talents and strengths and they were able diocese, or someone that values and encourages to take over and support others around them who Catholic education – thank you for what you have found this year wasn’t their year to shine. You will see done to build our college community this year. that the pandemic has not stopped our young people As we make plans for a successful 2021 at Kavanagh developing their skills and talents and enjoying the College, we will continue to value our community holistic college life we encourage them to have. and the powerful part it can play, and we will think Our ‘Wall of Fame’ in the auditorium foyer has run out about this quote of space! Even in the year that has been, when many from Michael events and opportunities were cancelled, ten of our Jordan – ‘Talent students still managed to receive national honours wins games, but in their chosen field. You will find them listed in this teamwork and publication. intelligence win championships.’ Having a strong college community and the culture that this creates, is one of the most important taonga Have a truly a school can have.
    [Show full text]
  • Saint Gave 'Wonderful Care'
    THE MON T HLY MAGAZINE FOR T HE CA T HOLI C S OF T HE DUNE D IN DIO C ESE HE ABLE T NovemberT 2009 T Issue No 149 Saint gave ‘wonderful care’ to sick and elderly THE “wonderful care” given to the sick and “When he went to look after the lep- elderly by St Jeanne Jugan was reflected ers, he realised he was signing his own in Dunedin diocese as the Little Sisters of death warrant,” Bishop Campbell said. the Poor “carry on that charism this part St Damian was a cousin of Mrs Anita of the world”, Bishop Colin Campbell told Wynn-Williams, of Dunedin. Her sons, Fr residents, families and friends at a Mass in Damian and Giles, went to Rome for the St Joseph’s Church, Brockville, on October canonisation. 31. Fr Wynn-Williams’ account of the St Cause to celebrate … Sr Marguerite “What inspired this dedicated woman Peter’s ceremony is on page 2. Frew, of Dunedin, with Bishop Colin came from the heart of Jesus. Here, our “It was extraordinarily calm and joyful,” Campbell in Rome after the canonisa- own sisters tell us and the world in a very Mr Wynn-Williams said. tion of Jeanne Jugan� special way what God is all about,” the The Dunedin chapter of Little Sisters bishop said. of the Poor was represented in Rome by In this issue… On October 11, Pope Benedict XVI Sr Marguerite Frew, who described the New Walk by Faith course �����������3 canonised five new saints, including occasion as “tremendous”. Jeanne Jugan, who founded the Little “It was wonderful,” she said.
    [Show full text]
  • Auckland District Round Results
    Auckland District Round Results Thursday 10 – Sunday 13 June 2021 BEST GROUP OVERALL GoodFellas, ACG Parnell College and Saint Kentigern College Sunny Le, Piano, ACG Parnell College Charles Sang, Piano, Saint Kentigern College Alex Bian, Percussion, Saint Kentigern College Jason Wong, Percussion, Saint Kentigern College Jenny McLeod | Music for Four HIGHLY COMMENDED Oddities, King’s College, St Kentigern College, Rangitoto College AHA, Cornwall Park District School, Parnell District School, Sunnyhills Primary School Trio Disordinata, King’s College, Tauranga Girls’ College, Westlake Boys High School Red Hedgehog, Macleans College, Glendowie College, Carmel College ADJUDICATOR AWARD Russian Empire, Westlake Girls High School, St Kenrigern College, Takapuna Grammar School, Westlake Boys High School KBB AWARDS Trio Burlesque, St Peter’s College, ACG Parnell College Petrus, Diocesan School for Girls, St Peter’s College, St Kentigern College Ornate , St Kentigern College, Avondale College, Auckland Grammar School, Diocesan School for Girls, St Cuthbert’s College, St Peter’s College Trio Anima, Rangitoto College The 2021 NZCT Chamber Music Contest is made possible with generous funding from: Auckland District Round Results Thursday 10 – Sunday 13 June 2021 BEST PERFORMANCE OF A NZ WORK GoodFellas, ACG Parnell College, St Kentigern College Jenny McLeod | Music for Four BEST PERFORMANCE OF AN ORIGINAL COMPOSITION WORK Moon Stars, Mt Albert Grammar School Mekal Covic | Two Worlds JUNIOR AWARD Quintet Brilliante, Auckland Grammar School, St Kentigern College, Macleans College NEWCOMERS AWARD Haydnseek, Diocesan School for Girls MOST ENGAGING PERFORMANCE AWARD Trio Élénk, Diocesan School for Girls The 2021 NZCT Chamber Music Contest is made possible with generous funding from: .
    [Show full text]
  • Rebel Sport 3X3 Basketball NZ Secondary Schools Champs 2021
    Rebel Sport 3X3 Basketball NZ Secondary Schools Champs 2021 DRAW JNR BOYS ELITE JNR BOYS ELITE JNR GIRLS ELITE Pool A Pool B Pool A Hastings Boys High School JA Hamilton Boys High School Black Westlake Girls High School A St Johns College Falcons Rosmini College Rotorua Girls High School A Rotorua Boys High School A Pukekohe High School Black Hamilton Girls High School A Rangitoto College Rongotai College Hastings Girls High School Mt Albert Grammar School St Peters School, Cambridge A Mt Albert Grammar School Gold Liston College St Andrews College Rangitoto College Kelston Boys High School St Marys College, Ponsonby St Peters School, Cambridge A St Andrews College Tauranga Girls College A SNR BOYS ELITE SNR BOYS ELITE SNR GIRLS ELITE SNR GIRLS ELITE Pool A Pool B Pool A Pool B Westlake Boys High School Rosmini College St Peters School Cambridge A Hamilton Girls High School St Johns College Eagles Rotorua Boys High School A St Marys College, Ponsonby Westlake Girls High School A Hamilton Boys High School A Rongotai College Sacred Heart Girls College, NP Rotorua Girls High School A St Peters College, Auckland Mana College Massey High School Queen Margaret College Hastings Boys High School A St Andrews College Te Kura Kokiri Wahine Hastings Girls High School Fraser High School Rangitoto College Buller High School St Andrews College Mt Albert Grammar School Te Aroha College Baradene College Rangitoto College One Tree Hill College Pukekohe High School Black Nga Taiatea Wharekura Tauranga Girls College Blue Kelston Boys High School Blue Waihi
    [Show full text]
  • Taste of Japan 2010: Haiku and Shodo Competition the Haiku
    Taste of Japan 2010: Haiku and shodo competition The haiku & shodo competition was run as part of Taste of Japan 2010 organized by the NZ Japan Society of Auckland Inc. with the support of the Consulate General of Japan. This competition aimed to provide an opportunity for learners of Japanese language to express their thoughts and feelings in a Japanese haiku poem and to experience the traditional Japanese art of calligraphy. Entry was open to high school students between year 10 and 13 who are studying Japanese at schools in New Zealand, and to the members of the NZ Japan Society of Auckland who are non-native speakers of Japanese. Participants were required to compose a haiku poem in Japanese, in the form of 3 lines consisting of 5, 7 and 5 sounds (one sound typically corresponds to one hiragana character), and write it on a long strip of paper vertically with a writing brush ( hude ) and ink ( sumi ). The competition was advertised through the following websites and mailing lists. • website for NZAJLT (New Zealand Association of Japanese Language Teachers) • NZJNET • website for the NZ Japan Society of Auckland Inc. ( www.nzjapan.net ) • News Letter posted by National Adviser of Japanese at ILANZ (International Languages Aotearoa New Zealand), Ms. Junko Tomooka We received a total of 143 entries from 13 schools for the high school section, and 4 entries for the NZJS section. Twenty haiku poems were shortlisted by two judges from our society and were passed to the Japanese language teachers at School of Languages, AUT who selected the winners.
    [Show full text]
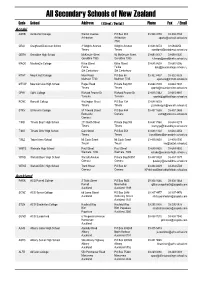
  • Secondary Schools of New Zealand
    All Secondary Schools of New Zealand Code School Address ( Street / Postal ) Phone Fax / Email Aoraki ASHB Ashburton College Walnut Avenue PO Box 204 03-308 4193 03-308 2104 Ashburton Ashburton [email protected] 7740 CRAI Craighead Diocesan School 3 Wrights Avenue Wrights Avenue 03-688 6074 03 6842250 Timaru Timaru [email protected] GERA Geraldine High School McKenzie Street 93 McKenzie Street 03-693 0017 03-693 0020 Geraldine 7930 Geraldine 7930 [email protected] MACK Mackenzie College Kirke Street Kirke Street 03-685 8603 03 685 8296 Fairlie Fairlie [email protected] Sth Canterbury Sth Canterbury MTHT Mount Hutt College Main Road PO Box 58 03-302 8437 03-302 8328 Methven 7730 Methven 7745 [email protected] MTVW Mountainview High School Pages Road Private Bag 907 03-684 7039 03-684 7037 Timaru Timaru [email protected] OPHI Opihi College Richard Pearse Dr Richard Pearse Dr 03-615 7442 03-615 9987 Temuka Temuka [email protected] RONC Roncalli College Wellington Street PO Box 138 03-688 6003 Timaru Timaru [email protected] STKV St Kevin's College 57 Taward Street PO Box 444 03-437 1665 03-437 2469 Redcastle Oamaru [email protected] Oamaru TIMB Timaru Boys' High School 211 North Street Private Bag 903 03-687 7560 03-688 8219 Timaru Timaru [email protected] TIMG Timaru Girls' High School Cain Street PO Box 558 03-688 1122 03-688 4254 Timaru Timaru [email protected] TWIZ Twizel Area School Mt Cook Street Mt Cook Street
    [Show full text]
  • Team Registrations.Xlsx
    Dunedin Netball Y7/8 Competition Festival Game Play R1 Game Play R2 School Game Play Courts* Pod 4.10pm 4.21pm Balmacewen Intermediate Balmac Yellow 5 5 Tahuna Normal Intermediate Tahuna 7A 5 9 A: 3.30pm Taieri College Taieri College Comets 9 5 Balmacewen Intermediate Balmac Grey 9 9 Bathgate Park School BGP Coyotes 8 8 Green Island School Green Island Steel 8 10 B: 3.30pm Kaikorai Valley College Whero 10 8 Liberton Christian School Liberton Gold 10 10 Balmacewen Intermediate Balmac Gold 11 11 Columba College Columba 8A 11 13 C: 3.30pm Taieri College Taieri College Tactix 13 11 Taieri College Taieri College Steel 13 13 Columba College Columba 7A 12 12 Kavanagh College Kavanagh 7 Gold 12 14 D: 3.30pm Tahuna Normal Intermediate Tahuna 7B 14 12 Balmacewen Intermediate Balmac Orange 14 14 Arthur Street School Arthur Street Steel 15 15 Kavanagh College Kavanagh 7/8 Blue 15 17 Kaikorai Valley College Kowhai 16 16 E: 3.30pm Portobello School Baybellos 16 15 Kavanagh College Kavanagh 7/8 Gold 17 17 Dunedin Rudolf Steiner School Steiner Salts 17 16 Balmacewen Intermediate Balmac Maroon 19 19 Kaikorai Valley College Matai 19 21 F: 3.30pm Bathgate Park School BGP Hyenas 21 19 Fairfield School (Dunedin) Fairfield Steel 21 21 *Please note teams go to these courts after completing the Dunedin Netball led NetballSmart Warmup. After 8mins they play another team from their pod. Dunedin Netball Y7/8 Competition Festival Game Play R1 Game Play R2 Game Play R3 School Game Play Courts* Pod 5.10pm 5.21pm 5.33pm Balmacewen Intermediate Balmac Silver 5 5 Dunedin
    [Show full text]
  • High School Preparation Program That Prepares Students for Entry Into a New Zealand High School
    KIWI ENGLISH ACADEMY HighHigh SchoolSchool PreparationPreparation Kiwi English Academy has a unique high school preparation program that prepares students for entry into a New Zealand high school. Since our separate high school campus opened in 1995 Kiwi English Academy has sent hundreds of students into high schools all around New Zealand. Programme Features A structured programme that includes General English plus subject-specific study once students have reached a certain level. Long-term students are encouraged to take Cambridge English for Schools test at the end of their programme. NZQA ( New Zealand Qualifications Authority) accredited programme – accredited to teach NCEA (National Certificate in Educational Achievement) unit standards in English, science, maths, accounting, economic theory and practice. Kiwi English Academy is one of the few English language schools in NZ that is accredited to offer these NCEA unit standards and the only school in central Auckland with this capability. Assessment methods linked to those at high school to ensure consistency for students. A disciplined environment where students are able to adjust academically, socially and personally to their new life in New Zealand. A mix of nationalities. Our junior programme attracts students from many different countries including Bra- zil, China, Hong Kong, Japan, Korea, New Caledonia Russia, Taiwan, Turkey and Vietnam. Students have the opportunity to make friends from around the world. Programme Length Support Services The length of the programme KiwiCare
    [Show full text]
  • Sideout April 2021
    SIDEOUT A P R I L 2 0 2 1 W E L C O M E W H A T ' S Welcome to this edition of the SideOut. The recent Secondary School Championships were a success, well C O M I N G U P done and thank you to everyone who was involved. Indoor Development Camps There's lots more volleyball coming up to look forward to North Island 22-23 April so make sure you keep an eye on our website and social South Island 28-29 April media for all the updates. In this edition: Inter Provincial 1. Chief Executive's Message Championships 2. Board Team Talk ASB Sports Centre, Wellington 3. NZSSVC Report 5-7 June 4. National Volleyball League 5. Events Page National Volleyball League 26-27 June, Auckland 10-11 July, Christchurch C H I E F E X E C U T I V E ' S M E S S A G E T O N I - M A R E E This week leads into the inaugural draft for the new National Volleyball League. It’s certainly a time of excitement and interest as VNZ launches the NVL with an online draft format for our top men’s and women’s athletes on Monday April 26th. Coaches are busy reviewing the over 200 athletes that have registered for the draft. With confirmed venues in Auckland (YMCA, Auckland Central) for June 26-27 and Christchurch (Pioneer Stadium) July 10-11, this is a marvellous opportunity for the NZ community to see top volleyball in our own country and I encourage those living close to those centres to support our athletes and the event in person.
    [Show full text]
  • Shadow a Leader Business, Economics and Law 2
    SHADOW A LEADER BUSINESS, ECONOMICS AND LAW 2 SHADOW A LEADER The aim of Shadow a Leader is to give secondary school students and AUT Business, Economics and Law students the opportunity to follow a business leader for a day and to understand what it takes to succeed in the leader’s profession. Students are identified as having future business leadership potential. Leadership Week takes place in the first week of July each year. Shadow a Leader is an initiative to support Leadership Week. 3 TEAMS OF THREE Shadow a Leader chooses year 13 secondary Secondary school business teachers and school business students and AUT Business, Heads of Department nominate their business Economics and Law students to “shadow” a students deserving of this initiative. These business leader for the day. are students managing successful Young Enterprise Scheme initiatives or those Shadow a Leader launched with four teams excelling in business studies. of three in 2012, successfully extended to over 50 teams of three in 2013, and to 75 AUT students bring their experience as teams thereafter. tertiary students and expertise of their chosen areas of study to Shadow a Leader Each team consists of a business leader, teams. They are charged with guiding their one secondary school student, and one younger student team members. AUT student. (COVER) VINCENT CHAN (AUT BUSINESS SCHOOL), MIKE MARR (GROUP GENERAL MANAGER, ADVANCED SECURITY GROUP), RAYHAN ARUL (MASSEY HIGH SCHOOL) (ABOVE) SUE FOLEY (DIRECTOR OF CORPORATE AFFAIRS, WESTPAC), MAJELLA ANERU (PAKURANGA COLLEGE), GABI DAVIS (AUT BUSINESS SCHOOL) (BELOW) TONY FALKENSTEIN (MANAGING DIRECTOR, JUST WATER INTERNATIONAL), ANTON VERA (AUT BUSINESS SCHOOL), EDAN BICHENO (EPSOM GIRLS GRAMMAR SCHOOL) 4 THE DAY The Shadow a Leader day begins with to prepare them for the day ahead and breakfast at AUT for all participating hear from one of the inspiring leaders in business leaders and students.
    [Show full text]
  • Honours Jazz Band 2019
    Honours Jazz Band 2019 ALTO SAX TROMBONE 1 Molly Manning Epsom Girls Grammar 1 Amy Laithwaite Baradene College 2 Charlie Harmer Rangitoto College 2 Jack Wood St Peter’s College 3 Nicholas Lee Pukekohe High School TENOR SAX 4 James Marriott (+ bass) Rutherford College 1 James Hancock Kings College 2 Joshua Sain Glendowie College GUITAR William Betham (tacet Groovin’ Hard) Dilworth College BARITONE SAX Daniel Piper Pukekohe High School PIANO Phoebe Kong Sancta Maria College TRUMPET 1 Peter Brzozowski Sancta Maria College BASS GUITAR 2 Hamish Butterworth-Snell St Peters College Alex Cooper ACG Parnell College 3 Sione Latu Dilworth College 4 Joshua Beanland Orewa College DRUMS 5 Miles Timmis (dbl. 1 in Apple Honey) Rangitoto College Ben Tan Long Bay College Honours Symphony Orchestra 2019 FLUTE TRUMPET 1 Catherine Chang Saint Kentigern College 1 Liam Wright Westlake Boys High School 2 Celesti Tan Lynfield College 2 Jenna Parkin ACG Parnell 3 Caitlin Halls (dbl.1 in Cave Weta) St Mary’s College PICCOLO 4 Mayna Tse (dbl.2 in Cave Weta) Glendowie College Micah Sullivan Lynfield College TROMBONE OBOE 1 Craig Lim Westlake Boys High School 1 Catherine Oh Rangitoto College 2 Alex Jin Macleans College 2 Ashton Jarred Lin Saint Peter’s College BASS TROMBONE CLARINET John Yang (tbn. 3 in Swan Lake) Macleans College 1 Matthew Donnelly Saint Peter’s College 2 Rosie Kim Epsom Girls Grammar School TUBA Teresa Gu Diocesan School for Girls BASS CLARINET Cameron Howe (Cave Weta only) Rosehill College TIMPANI Maia O’Connell St Mary’s College BASSOON 1 Ricky
    [Show full text]