Presto! Digitization: Part I
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Notices of the American Mathematical Society
ISSN 0002-9920 of the American Mathematical Society February 2006 Volume 53, Number 2 Math Circles and Olympiads MSRI Asks: Is the U.S. Coming of Age? page 200 A System of Axioms of Set Theory for the Rationalists page 206 Durham Meeting page 299 San Francisco Meeting page 302 ICM Madrid 2006 (see page 213) > To mak• an antmat•d tub• plot Animated Tube Plot 1 Type an expression in one or :;)~~~G~~~t;~~i~~~~~~~~~~~~~:rtwo ' 2 Wrth the insertion point in the 3 Open the Plot Properties dialog the same variables Tl'le next animation shows • knot Plot 30 Animated + Tube Scientific Word ... version 5.5 Scientific Word"' offers the same features as Scientific WorkPlace, without the computer algebra system. Editors INTERNATIONAL Morris Weisfeld Editor-in-Chief Enrico Arbarello MATHEMATICS Joseph Bernstein Enrico Bombieri Richard E. Borcherds Alexei Borodin RESEARCH PAPERS Jean Bourgain Marc Burger James W. Cogdell http://www.hindawi.com/journals/imrp/ Tobias Colding Corrado De Concini IMRP provides very fast publication of lengthy research articles of high current interest in Percy Deift all areas of mathematics. All articles are fully refereed and are judged by their contribution Robbert Dijkgraaf to the advancement of the state of the science of mathematics. Issues are published as S. K. Donaldson frequently as necessary. Each issue will contain only one article. IMRP is expected to publish 400± pages in 2006. Yakov Eliashberg Edward Frenkel Articles of at least 50 pages are welcome and all articles are refereed and judged for Emmanuel Hebey correctness, interest, originality, depth, and applicability. Submissions are made by e-mail to Dennis Hejhal [email protected]. -

By Hand and Eye: Dance in the Space of the Artist's Book
By Hand and Eye: Dance in the Space of the Artist’s Book Judith May Walton School of Communication and the Arts, Faculty of Arts, Education, and Human Development, Victoria University Submitted in partial fulfillment of the requirements of the degree of Doctor of Philosophy (by performance / exhibition) (December, 2010) Abstract By Hand and Eye: Dance in the Space of the Artist’s Book is a practice-based research project that explores what potential there might be for dancing, or an expanded notion of dance, to be found and/or created in book form. For instance, how might a book dance, rehearse its contents? What relationships can be found or forged between the body and the artist’s book: the movement of the eye, the spacing of thought, temporality and duration, and the choreography of the page? These propositions have been explored and expanded through a tactile, experiential examination of selected artists’ books from the National Art Library (NAL) of the Victoria & Albert Museum, a translation/re-working of existing performances into book form, and the creation of unique artist-made books. The project seeks to embody and enact concepts and questions considered through the research; signalling, suggesting, amplifying, and marking, gestures and rehearsals for movement. This process has resulted in three outcomes: an exhibition of artist-made books with a performed opening, a recuperation of selected past performances remembered and re-made in book form, and a series of written discussion papers and accompanying video essays based on the artists’ book collection at the NAL at the Victoria and Albert Museum, London. -

Kite Lines Is the Comprehensive International Winners! in the Cerf-Volant Club De France's Kite Aerial Journal of Kiting and the Only Magazine of Its Kind in America
Contents Copyright © 1981 Aeolus Press, Inc. Reproduction in any form, in whole or in part is strictly prohibited without prior written Volume 4, Number 1, Summer-Fall 1981 consent of the publisher . Kite Lines is the comprehensive international Winners! in the Cerf-Volant Club de France's Kite Aerial journal of kiting and the only magazine of its kind in America . It is published by Aeolus Photography Contest / 22 Press, Inc ., of Baltimore, MD, with editorial See and decide for yourself if you agree with the judges . Full-size offices at 7106 Campfield Road, Baltimore, reproductions of the first and second place winners, Tom Pratt of MD 21207, telephone : (301) 484-6287 . Scotland and Garry Woodcock of Canada, plus reduced-size prints of Kite Lines is endorsed by the international Kitefliers Association : and is on file in the the three runners-up . With details of the systems used and background libraries of the National Air and Space Museum, on the conducting of the contest by the Club . Smithsonian ; the National Oceanic and Atmo- Mastering Nylon, or-Everything about Nylon that I've Learned spheric Sciences Administration ; the National from Experience and Soaked Up from my Friends / 25 Geographic ; and the University of Notre . William Tyrrell, Jr., with illustrations by Cathy Pasquale . Dame's Sports and Games Research Collection By G An eight-page special pull-out feature that answers many of the Founder: Robert M . Ingraham technical questions you're likely to have about rip-stop and how to Publisher : Aeolus Press, Inc . work with it in kitemaking . With source list . -

Pure Spinors to Associative Triples to Zero-Divisors
Pure Spinors to Associative Triples to Zero-Divisors Frank Dodd (Tony) Smith, Jr. - 2012 Abstract: Both Clifford Algebras and Cayley-Dickson Algebras can be used to construct Physics Models. Clifford and Cayley-Dickson Algebras have in common Real Numbers, Complex Numbers, and Quaternions, but in higher dimensions Clifford and Cayley-Dickson diverge. This paper is an attempt to explore the relationship between higher-dimensional Clifford and Cayley-Dickson Algebras by comparing Projective Pure Spinors of Clifford Algebras with Zero-Divisor structures of Cayley-Dickson Algebras. 1 Pure Spinors to Associative Triples to Zero-Divisors Frank Dodd (Tony) Smith, Jr. - 2012 Robert de Marrais and Guillermo Moreno, pioneers in studying Zero-Divisors, unfortunately have passed (2011 and 2006). Pure Spinors to Associative Triples ..... page 2 Associative Triples to Loops ............... page 3 Loops to Zero-Divisors ....................... page 6 New Phenomena at C32 = T32 ........... page 9 Zero-Divisor Annihilator Geometry .... page 17 Pure Spinors to Associative Triples Pure spinors are those spinors that can be represented by simple exterior wedge products of vectors. For Cl(2n) they can be described in terms of bivectors Spin(2n) and Spin(n) based on the twistor space Spin(2n)/U(n) = Spin(n) x Spin(n). Since (1/2)((1/2)(2n)(2n-1)-n^2) = (1/2)(2n^2-n-n^2) = = (1/2)(n(n-1)) Penrose and Rindler (Spinors and Spacetime v.2) describe Cl(2n) projective pure half-spinors as Spin(n) so that the Cl(2n) full space of pure half-spinors has dimension dim(Spin(n)) -

The Golden Age of Kites?)
The Kiteflier, Issue 94 Page 15 Kite for a Purpose (The Golden Age of Kites?) 1 Introduction Bell was a Scottish/Canadian who made his fortune in My purpose in writing these articles is not primarily the his- the U.S.A., Cody, an American who adopted British na- tory of kiting but in the development of kites as we know tionality and Hargrave an English born Australian. them, i.e. to explain and inform about kites seen in the air · While it was important to Cody, Eddy and Conyne that today. their inventions should be patented, Bell (whose wealth cam from the heavily patented telephone) was open with There are as usual diagrams, plans and photos. As before his scientific enquiries and Hargrave would not patent capital letters (PELHAM) means a full reference in the bibliog- anything as he believed knowledge should be free to all. raphy. The layout is: · Again two of the five have a wider fame than designing and flying kites – Cody built the first aircraft in England 1. Introduction and Bell had the telephone. 2. Needs for kites 3. The fliers Usually a period of rapid invention and development is caused 4. Omissions and exceptions by the availability of new materials, new techniques or new needs. In this case there was little change in materials – It is sometimes said that the last years of the 19 th century kites could/would be made of silk or fine cotton using bamboo and the first years of the 20th century were the ‘Golden Age or hardwood right through the period. -

Theory of Trigintaduonion Emanation and Origins of Α and Π
Theory of Trigintaduonion Emanation and Origins of and Stephen Winters-Hilt Meta Logos Systems Aurora, Colorado Abstract In this paper a specific form of maximal information propagation is explored, from which the origins of , , and fractal reality are revealed. Introduction The new unification approach described here gives a precise derivation for the mysterious physics constant (the fine-structure constant) from the mathematical physics formalism providing maximal information propagation, with being the maximal perturbation amount. Furthermore, the new unification provides that the structure of the space of initial ‘propagation’ (with initial propagation being referred to as ‘emanation’) has a precise derivation, with a unit-norm perturbative limit that leads to an iterative-map-like computed (a limit that is precisely related to the Feigenbaum bifurcation constant and thus fractal). The computed can also, by a maximal information propagation argument, provide a derivation for the mathematical constant . The ideal constructs of planar geometry, and related such via complex analysis, give methods for calculation of to incredibly high precision (trillions of digits), thereby providing an indirect derivation of to similar precision. Propagation in 10 dimensions (chiral, fermionic) and 26 dimensions (bosonic) is indicated [1-3], in agreement with string theory. Furthermore a preliminary result showing a relation between the Feigenbaum bifurcation constant and , consistent with the hypercomplex algebras indicated in the Emanator Theory, suggest an individual object trajectory with 36=10+26 degrees of freedom (indicative of heterotic strings). The overall (any/all chirality) propagation degrees of freedom, 78, are also in agreement with the number of generators in string gauge symmetries [4]. -

The Cayley-Dickson Construction in ACL2
The Cayley-Dickson Construction in ACL2 John Cowles Ruben Gamboa University of Wyoming Laramie, WY fcowles,[email protected] The Cayley-Dickson Construction is a generalization of the familiar construction of the complex numbers from pairs of real numbers. The complex numbers can be viewed as two-dimensional vectors equipped with a multiplication. The construction can be used to construct, not only the two-dimensional Complex Numbers, but also the four-dimensional Quaternions and the eight-dimensional Octonions. Each of these vector spaces has a vector multiplication, v1 • v2, that satisfies: 1. Each nonzero vector, v, has a multiplicative inverse v−1. 2. For the Euclidean length of a vector jvj, jv1 • v2j = jv1j · jv2j Real numbers can also be viewed as (one-dimensional) vectors with the above two properties. ACL2(r) is used to explore this question: Given a vector space, equipped with a multiplication, satisfying the Euclidean length condition 2, given above. Make pairs of vectors into “new” vectors with a multiplication. When do the newly constructed vectors also satisfy condition 2? 1 Cayley-Dickson Construction Given a vector space, with vector addition, v1 + v2; vector minus −v; a zero vector~0; scalar multiplica- tion by real number a, a ◦ v; a unit vector~1; and vector multiplication v1 • v2; satisfying the Euclidean length condition jv1 • v2j = jv1j · jv2j (2). 2 2 Define the norm of vector v by kvk = jvj . Since jv1 • v2j = jv1j · jv2j is equivalent to jv1 • v2j = 2 2 jv1j · jv2j , the Euclidean length condition is equivalent to kv1 • v2k = kv1k · kv2k: Recall the dot (or inner) product, of n-dimensional vectors, is defined by (x1;:::;xn) (y1;:::;yn) = x1 · y1 + ··· + xn · yn n = ∑ xi · yi i=1 Then Euclidean length and norm of vector v are given by p jvj = v v kvk = v v: Except for vector multiplication, it is easy to treat ordered pairs of vectors, (v1;v2), as vectors: 1. -

Similarity and Consimilarity of Elements in Real Cayley-Dickson Algebras
SIMILARITY AND CONSIMILARITY OF ELEMENTS IN REAL CAYLEY-DICKSON ALGEBRAS Yongge Tian Department of Mathematics and Statistics Queen’s University Kingston, Ontario, Canada K7L 3N6 e-mail:[email protected] October 30, 2018 Abstract. Similarity and consimilarity of elements in the real quaternion, octonion, and sedenion algebras, as well as in the general real Cayley-Dickson algebras are considered by solving the two fundamental equations ax = xb and ax = xb in these algebras. Some consequences are also presented. AMS mathematics subject classifications: 17A05, 17A35. Key words: quaternions, octonions, sedenions, Cayley-Dickson algebras, equations, similarity, consim- ilarity. 1. Introduction We consider in the article how to establish the concepts of similarity and consimilarity for ele- n arXiv:math-ph/0003031v1 26 Mar 2000 ments in the real quaternion, octonion and sedenion algebras, as well as in the 2 -dimensional real Cayley-Dickson algebras. This consideration is motivated by some recent work on eigen- values and eigenvectors, as well as similarity of matrices over the real quaternion and octonion algebras(see [5] and [18]). In order to establish a set of complete theory on eigenvalues and eigenvectors, as well as similarity of matrices over the quaternion, octonion, sedenion alge- bras, as well as the general real Cayley-Dickson algebras, one must first consider a basic problem— how to characterize similarity of elements in these algebras, which leads us to the work in this article. Throughout , , and denote the real quaternion, octonion, and sedenion algebras, H O S n respectively; n denotes the 2 -dimensional real Cayley-Dickson algebra, and denote A R C the real and complex number fields, respectively. -
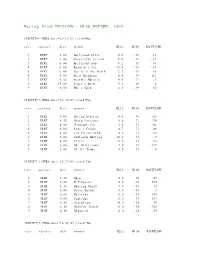
Racing Flow-TM FLOW + BIAS REPORT: 2009
Racing Flow-TM FLOW + BIAS REPORT: 2009 CIRCUIT=1-NYRA date=12/31/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 5.50 Hollywood Hills 0.0 -19 13 2 DIRT 6.00 Successful friend 5.0 -19 -19 3 DIRT 6.00 Brilliant Son 5.2 -19 47 4 DIRT 6.00 Raynick's Jet 10.6 -19 -61 5 DIRT 6.00 Yes It's the Truth 2.7 -19 65 6 DIRT 8.00 Keep Thinking 0.0 -19 -112 7 DIRT 8.32 Storm's Majesty 4.0 -19 6 8 DIRT 13.00 Tiger's Rock 9.4 -19 6 9 DIRT 8.50 Mel's Gold 2.5 -19 69 CIRCUIT=1-NYRA date=12/30/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.00 Spring Elusion 4.4 71 -68 2 DIRT 8.32 Sharp Instinct 0.0 71 -74 3 DIRT 6.00 O'Sotopretty 4.0 71 -61 4 DIRT 6.00 Indy's Forum 4.7 71 -46 5 DIRT 6.00 Ten Carrot Nikki 0.0 71 -18 6 DIRT 8.00 Sawtooth Moutain 12.1 71 9 7 DIRT 6.00 Cleric 0.6 71 -73 8 DIRT 6.00 Mt. Glittermore 4.0 71 -119 9 DIRT 6.00 Of All Times 0.0 71 0 CIRCUIT=1-NYRA date=12/27/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.50 Quip 4.5 -38 49 2 DIRT 6.00 E Z Passer 4.2 -38 255 3 DIRT 8.32 Dancing Daisy 7.9 -38 14 4 DIRT 6.00 Risky Rachel 0.0 -38 8 5 DIRT 6.00 Kaffiend 0.0 -38 150 6 DIRT 6.00 Capridge 6.2 -38 187 7 DIRT 8.50 Stargleam 14.5 -38 76 8 DIRT 8.50 Wishful Tomcat 0.0 -38 -203 9 DIRT 8.50 Midwatch 0.0 -38 -59 CIRCUIT=1-NYRA date=12/26/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 6.00 Papaleo 7.0 108 129 2 DIRT 6.00 Overcommunication 1.0 108 -72 3 DIRT 6.00 Digger 0.0 108 -211 4 DIRT 6.00 Bryan Kicks 0.0 108 136 5 DIRT 6.00 We Get It 16.8 108 129 6 DIRT 6.00 Yawanna Trust 4.5 108 -21 7 DIRT 6.00 Smarty Karakorum 6.5 108 83 8 DIRT 8.32 Almighty Silver 18.7 108 133 9 DIRT 8.32 Offlee Cool 0.0 108 -60 CIRCUIT=1-NYRA date=12/13/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.32 Crafty Bear 3.0 -158 -139 2 DIRT 6.00 Cheers Darling 0.5 -158 61 3 DIRT 6.00 Iberian Gate 3.0 -158 154 4 DIRT 6.00 Pewter 0.5 -158 8 5 DIRT 6.00 Wolfson 6.2 -158 86 6 DIRT 6.00 Mr. -

Arthur Raff Oral History
"0" Preface Page and Introductory Page An introduction by Art Raff to the following typed transcription and accompanying audio tapes: I started this on 28 March 1996 with a completely unplanned narrative ofreminiscences about my days of working for the Marine Physical Laboratory. I told ofevents just as they happened to come to mind, and thus the sequence is in no way chronological. Betty Shor typed a transcript from this fIrst tape. When I read the transcript I was embarrassed by the unprofessional quality ofmy audio tape. I took the liberty quite some time later to severely edit the transcript and add more events ofinterest, but left it in its original nonchronological sequence. So now in July 1996 I am making an audio to accompany the edited and enlarged transcript by reading the transcript to an audio tape recorder. I have compiled an index to help an interested person years from now to locate some event. This index will accompany the final transcript and audio tape. A Index to Typed Transcript of Art Raffs Reminiscing Page no. \\0 'I Preface Page and Introductory Page THE FOLLOWING FEW SUBJECfS ARE ON CASSETTE NO.1 Introduction: My name is Arthur D. Raff, etc. _\ Editorial note by Betty Shor and Art Raff -' The early MPL staff _1 Met Dr. Eckart at UCLA. Suggested I drive down to San Diego and look over MPL Raitt interviewed me and hired me at $220 per month First job was to read records on a one-of-a-kind fathometer Early history of Stranger Deep scattering layer discovered by Eyring, Raitt, and Christensen When Stranger scrapped, bought for the value oflead in bottom About Finn Outler The Saluda, a gold plated ship. -
![Arxiv:2012.03874V2 [Cs.CV] 11 Dec 2020 Dent Modalities](https://docslib.b-cdn.net/cover/9937/arxiv-2012-03874v2-cs-cv-11-dec-2020-dent-modalities-2259937.webp)
Arxiv:2012.03874V2 [Cs.CV] 11 Dec 2020 Dent Modalities
Traffic flow prediction using Deep Sedenion Networks Alabi Bojesomo, Hasan Al-Marzouqi, Panos Liatsis Electrical Engineering and Computer Science Department, Khalifa University, Abu Dhabi, UAE. {100046384, hasan.almarzouqi, panos.liatsis}@ku.ac.ae Abstract In this paper, we present our solution to the Traffic4cast2020 traffic prediction challenge. In this competition, participants are to predict future traffic parameters (speed and volume) in three different cities: Berlin, Istanbul and Moscow. The information provided includes nine channels where the first eight represent the speed and volume for four different direction of traffic (NE, NW, SE and SW), while the last channel is used to indicate presence of traffic incidents. The expected output should have the first 8 channels of the input at six future timing intervals (5, 10, 15, 30, 45, and 60min), while a one hour duration of past traffic data, in 5mins intervals, are provided as input. We solve the problem using a novel sedenion U-Net neural network. Sedenion networks provide the means for efficient encoding of correlated multimodal datasets. We use 12 of the 15 sedenion imaginary parts for the dynamic inputs and the real sedenion component is used for the static input. The sedenion output of the network is used to represent the multimodal traffic predictions. Proposed system achieved a validation MSE of 1.33e-3 and a test MSE of 1.31e-3. 1 Introduction In this contribution, we briefly summarize the methodology and experiments in tackling the Traf- fic4cast challenge 2020 [1]. The aim of the challenge is to predict future traffic flow volume and speed using traffic information projected on high resolution city maps. -

On Cosets in Split Extensions of Hypercomplex Numbers
ON COSETS IN SPLIT EXTENSIONS OF HYPERCOMPLEX NUMBERS BY MUSYOKA DAVID MWANZIA REG NO. I56/CE/28760/2015 A Project submitted in partial fulfilment of the requirements for the Award of the Degree of Master of Science in Pure Mathematics in the School of Pure and Applied Sciences of Kenyatta University. June, 2019 i DECLARATION This project is my original work and has not been submitted for any degree award in any other university. Signature ……………………………………….. Date ………………………………………… MUSYOKA DAVID MWANZIA B. ED (Hons) This research project has been submitted for examination with my approval as a University Supervisor. Signature ……………………………………….. Date …………………………………………. DR. LYDIA N. NJUGUNA. MATHEMATICS DEPARTMENT KENYATTA UNIVERSITY. ii DEDICATION I would like to dedicate this work to my dear wife Fey and daughter Julie for their constant encouragement as I pursued my academic goals. I also dedicate my work to my parents and siblings for their unfailing support in my academic journey. iii ACKNOWLEDGEMENT First, I give glory to the Almighty God, I thank Him for the gift of life, good health and an opportunity to study. Indeed, all my efforts would have been in vain if He did not guide me. Secondly, I would like to acknowledge my supervisor Dr. Lydia N. Njuguna for her continued guidance especially in the field of Loop Theory, throughout the time I was preparing my project. She was always ready every week to guide me where necessary. I wish also to thank all my lecturers in the Department of Mathematics of Kenyatta University for having taught me in various units in Pure Mathematics.