Pavement Structural Evaluation at the Network Level: Final Report
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Voices of Children and Young People
2003 - 2013 126 MILLION CONTActS REWIND RWD << The Voices of Children and Young People GIVING A VOICE TO CHILDREN AND YOUNG PEOPLE WORLDWIDE The Global Network of Child Helplines 173 Members in 141 Countries - 124 Full Members • Albania Child Rights CA • Indonesia TESA 129 Protection • Algeria Nada • Iran Sedaye Yara • Romania Asociata Telefonul Copilului • Argentina Línea 102 CABA • Iraq Kurdistan Iraqi Child Helpline • Russian NFPCC • Argentina Línea 102 Province BsAs • Ireland ISPCC Childline • Saudi Arabia National Family Safety Programme • Aruba Telefon Pa Hubentud • Israel Natal Hotline • Senegal Centre GINDDI • Australia Kids Help Line • Italy Telefono Azzurro • Serbia SOS Childline • Austria Rat Auf Draht 147 • Japan Childline Support Center Japan (NPO) • Sierra Leone Don Bosco Fambul • Bahrain Bahraini Child Helpline • Jordan 110 for Families and Children • Singapore Tinkle Friend Helpline • Bangladesh Aparajeyo Bangladesh • Kazakhstan Balaga Komek (Union of Crisis • Slovakia LDI • Belgium (KJT) Kinder- en Jongerentelefoon Centres) • Slovenia TOM • Bosnia Herzegovina SOS 1209 • Kenya Childline Kenya • South Africa Childline South Africa • Botswana Childline Botswana • Latvia Children Youth Trust Phone • Spain Telefono ANAR Spain • Brazil Alo 123! • Latvia Hotline 8006008 • Sri Lanka Childline Sri Lanka 1929 (National Child • Brazil Safernet • Lesotho Childline Lesotho Protection Authority) • Brunei Helpline 141 • Lithuania Vaiku Linija • Sri Lanka Lama Sarana (Don Bosco) • Burkina Faso Direction Generale de L’Encadrement • Luxemburg -
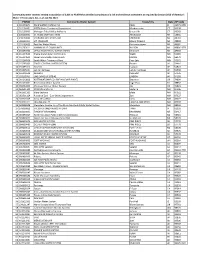
All Small-Sized Cwss That Have Certified Completion of Their RRA (Pdf)
Community water systems serving a population of 3,001 to 49,999 that certified completion of a risk and resilience assessment as required by Section 2013 of America's Water Infrastructure Act, as of July 30, 2021. PWSID Community Water System Town/City State ZIP Code 1 001570671 PACE WATER SYSTEM, INC. PACE FL 32571-0750 2 010106001 MPTN Water Treatment Department Mashantucket CT 06338 3 010109005 Mohegan Tribal Utility Authority Uncasville CT 06382 4 020000005 ST. REGIS MOHAWK TRIBE Akwesasne NY 13655 5 043740039 CHEROKEE WATER SYSTEM CHEROKEE NC 28719 6 055293201 MT. PLEASANT Mount Pleasant MI 48858 7 055293603 East Bay Water Works Peshawbestown MI 49682 8 055293611 HANNAHVILLE COMMUNITY WILSON MI 49896-9728 9 055293702 LITTLE RIVER TRIBAL WATER SYSTEM Manistee MI 49660 10 055294502 Prairie Island Indian Community Welch MN 55089 11 055294503 Lower Sioux Indian Community Morton MN 56270 12 055294506 South Water Treatment Plant Prior Lake MN 55372 13 055295003 SOUTH-CENTRAL WATER SYSTEM Bowler WI 54416 14 055295310 Giiwedin Hayward WI 54843 15 055295401 Lac du Flambeau Lac du Flambeau WI 54538 16 055295508 KESHENA KESHENA WI 54135 17 055295703 ONEIDA #1 OR SITE #1 ONEIDA WI 54155 18 061020808 POTTAWATOMIE CO. RWD #3 (DALE PLANT) Shawnee OK 74804 19 061620001 Reservation Water System Eagle Pass TX 78852 20 062004336 Chicksaw Winstar Water System Ada OK 74821 21 063501100 POJOAQUE SOUTH Santa Fe NM 87506 22 063501109 Isleta Eastside Isleta NM 87022 23 063501124 Pueblo of Zuni - Zuni Utility Department Zuni NM 87327 24 063503109 Isleta Shea Whiff Isleta NM 87022 25 063503111 LAGUNA VALLEY LAGUNA, NM 87026 NM 87007 26 063506008 Mescalero Apache Inn of the Mountain Gods Public Water System Mescalero NM 88340 27 070000003 SAC & FOX (MESKWAKI) IN IOWA TAMA IA 52339 28 083090091 TOWN OF BROWNING BROWNING MT 59417 29 083890023 Turtle Mountain Public Utilities Commission Belcourt ND 58316 30 083890025 Spirit Lake Water Management RWS St. -

THE INCOMPLETE GUIDE to AIRFOIL USAGE David Lednicer
THE INCOMPLETE GUIDE TO AIRFOIL USAGE David Lednicer Analytical Methods, Inc. 2133 152nd Ave NE Redmond, WA 98052 [email protected] Conventional Aircraft: Wing Root Airfoil Wing Tip Airfoil 3Xtrim 3X47 Ultra TsAGI R-3 (15.5%) TsAGI R-3 (15.5%) 3Xtrim 3X55 Trener TsAGI R-3 (15.5%) TsAGI R-3 (15.5%) AA 65-2 Canario Clark Y Clark Y AAA Vision NACA 63A415 NACA 63A415 AAI AA-2 Mamba NACA 4412 NACA 4412 AAI RQ-2 Pioneer NACA 4415 NACA 4415 AAI Shadow 200 NACA 4415 NACA 4415 AAI Shadow 400 NACA 4415 ? NACA 4415 ? AAMSA Quail Commander Clark Y Clark Y AAMSA Sparrow Commander Clark Y Clark Y Abaris Golden Arrow NACA 65-215 NACA 65-215 ABC Robin RAF-34 RAF-34 Abe Midget V Goettingen 387 Goettingen 387 Abe Mizet II Goettingen 387 Goettingen 387 Abrams Explorer NACA 23018 NACA 23009 Ace Baby Ace Clark Y mod Clark Y mod Ackland Legend Viken GTO Viken GTO Adam Aircraft A500 NASA LS(1)-0417 NASA LS(1)-0417 Adam Aircraft A700 NASA LS(1)-0417 NASA LS(1)-0417 Addyman S.T.G. Goettingen 436 Goettingen 436 AER Pegaso M 100S NACA 63-618 NACA 63-615 mod AerItalia G222 (C-27) NACA 64A315.2 ? NACA 64A315.2 ? AerItalia/AerMacchi/Embraer AMX ? 12% ? 12% AerMacchi AM-3 NACA 23016 NACA 4412 AerMacchi MB.308 NACA 230?? NACA 230?? AerMacchi MB.314 NACA 230?? NACA 230?? AerMacchi MB.320 NACA 230?? NACA 230?? AerMacchi MB.326 NACA 64A114 NACA 64A212 AerMacchi MB.336 NACA 64A114 NACA 64A212 AerMacchi MB.339 NACA 64A114 NACA 64A212 AerMacchi MC.200 Saetta NACA 23018 NACA 23009 AerMacchi MC.201 NACA 23018 NACA 23009 AerMacchi MC.202 Folgore NACA 23018 NACA 23009 AerMacchi -

Public Wholesale Water Supply District Status
Kansas Department of Health and Environment January 2017 Public Water Supply Section Capacity Development Program Public Wholesale Water Supply District Status Date Water Source Status Public Wholesale Water Formed Supply District PWWSD #1 Edgerton 8/15/77 None Dissolved – 1983 Gardner Spring Hill Johnson Co. RWDs 1, 2, 3, 5, 6, 6-A, 7 PWWSD #2 Melvern 5/1/78 None Dissolved – Mid 1980s Revived in 1989 as Waverly PWWSD #12 with expanded membership. (AN Co. RWD 4 & OS Co. RWD 4) PWWSD #3 Garnett 9/1/78 None Inactive – Garnett built lake and sells to AN Anderson Co. RWDs 2, 4, 6 Co. RWDs 4 & 6 PWWSD #4 Altamont 9/30/80 Big Hill Lake— Active – Water production for members since Bartlett KWO Water 1985 Cherryvale Marketing Contract Edna Mound Valley Labette Co. RWDs 3, 5, 7, 8 Montgomery Co. RWDs 2, 6, 12 Population Served: 10,264 (12 PWS) PWWSD #5 Colony La Harpe 9/16/80 Neosho River— Active – Water production for members since Moran Walnut Cottonwood/Neosho 1985 with a water treatment plant near the Allen Co. RWDs 4, 6, 8, 16 Assurance District Neosho River Anderson Co. RWD 5 Kincaid Bourbon Co. RWD 2C Fulton Prescott Neosho RWD 2 Population Served: 13,541 (14 PWS) PWWSD #6 Inactive – participants now purchase directly Tonganoxie 5/21/82 None from Bonner Springs Leavenworth Co. RWDs 6 & 9 PWWSD #7 Sedgwick Co. 12/22/82 Unknown Unknown Sedgwick Fire District #1 PWWSD #8 Butler Co. RWD 3 7/26/82 City of El Dorado Active – Supplies water to members through a State Park at El Dorado Lake water purchase contract with El Dorado Population Served: 1,577 (2 PWS) PWWSD #9 Gridley Hamilton 7/1/85 None Inactive – Gridley and Hamilton purchase from Virgil Burlington and Madison, respectively and Greenwood Co. -

Kansas Water Plan, Clean Drinking Water Fee Provide Help to 406 Systems in FY08
Summary Report Kansas Water Plan, Clean Drinking Water Fee provide help to 406 systems in FY08 ansas Rural Water Association has provided In FY08, the contract enabled KRWA to provide assistance to technical assistance to public Kwater systems through a 406 individual public water systems. These consisted of 242 contract funded through the different cities and 164 rural water systems. The Kansas Water Kansas Water Plan since 1992. In several recent years, the Kansas Office also assigned 97 water conservation plans to KRWA. Department of Health and Environment (KDHE) provided supplemental funding to the program. This article summarizes What services were provided? contract. In FY08, technical the work from July 1, 2007 to June In FY08, the contract enabled assistance was funded as an 30, 2008. A summary booklet was KRWA to provide assistance to 406 expenditure of the Clean Drinking provided to all members of the individual public water systems. Water Fee. Kansas Water Authority and mailed These consisted of 242 different cities Why all that history? Well, to each Basin Advisory Committee and 164 rural water systems. The KRWA operates numerous other member. The report is also posted on Kansas Water Office also assigned 97 contracts. Funding for those is either the KRWA Web site; the system water conservation plans to KRWA. through National Rural Water contacts are ‘searchable’. This paper Since 2003, 110 plans have been Association or a contract that allows copy will reach water system approved, 30 have been revised and KDHE to use federal set-asides from representatives who may not have submitted back to systems and 30 the drinking water revolving loan Internet access. -

Make a New Years' Source Water Resolution
This issue of “The Clarifier” is published by the Kansas Rural Water Association and is provided to water and wastewater utilities, associate members, agencies and other friends. Have a comment? Send it to KRWA at P.O. Box 226, Seneca, KS 66538; ph. 785/336-3760; e-mail: [email protected]. This newsletter is in addition to KRWA’s regular news magazine, The Kansas Lifeline. December 2016 Vol. 5 Make a New Years’ Source Water Resolution he Kansas Rural Water Association has T provided, at no charge, to public water supply systems, source water protection technical assistance since 1996. The first wellhead protection plan written with KRWA assistance and adopted by a public water supply system appears to have occurred in 1999. There have been several different staff members doing this work for the last 20 years, but none have had a longer tenure than geologist Doug Helmke. Doug started working for KRWA in 2000, to provide water rights assistance, and a few years later, started working in the Environmental Protection Agency-funded wellhead protection program which is This municipal well has soybeans planted within the 100-foot "pollution-free" administered through the National Rural easement. The lack of grass around the well pad suggests that a herbicide has been Water Association. Water rights assistance sprayed very close to the well and the water level measurement tube. The landowner continued to be an important service will be given information about agricultural buffers that may help his tenant and offered in conjunction with wellhead chemical applicators respect the public water supply system's easement. -
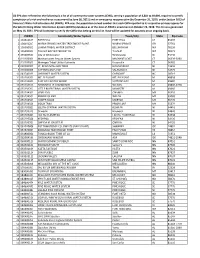
AWIA Small Size and WS RRA Report 05142021.Xlsx
US EPA data reflect that the following is a list of all community water systems (CWS), serving a population of 3,301 to 49,999, required to certify completion of a risk and resilience assessment (by June 30, 2021) and an emergency response plan (by December 31, 2021) under Section 2013 of America's Water Infrastructure Act (AWIA). EPA uses the population served number that each CWS reported to its respective primacy agency for the Safe Drinking Water Information System (SDWIS) database as of the date of AWIA’s enactment on October 23, 2018. This list was generated on May 14, 2021. EPA will continue to verify the CWSs that belong on this list. Data will be updated for accuracy on an ongoing basis. PWSID Community Water System Town/City State Zip Code 1 101612109 FORT HALL FORT HALL CA 83203 2 104101247 WARM SPRINGS WATER TREATMENT PLANT WARM SPRINGS OR 97761 3 105300002 LUMMI TRIBAL WATER DISTRICT BELLINGHAM WA 98226 4 105300003 TULALIP BAY WATER DIST #1 TULALIP WA 98271 5 265005620 City of Whitewater Whitewater WI 53190 6 010106001 Mashantucket Pequot Water System MASHANTUCKET CT 06339-3060 7 010109005 Mohegan Tribal Utility Authority Uncasville CT 06382 8 020000005 ST. REGIS MOHAWK TRIBE HOGANSBURG NY 13655 9 020000008 CATTARAUGUS CWS SALAMANCA NY 14779 10 043740039 CHEROKEE WATER SYSTEM CHEROKEE NC 28719 11 055293201 MT. PLEASANT MT. PLEASANT MI 48858 12 055293603 EAST BAY WATER WORKS SUTTONS BAY MI 49682 13 055293611 HANNAHVILLE COMMUNITY WILSON MI 49896-9728 14 055293702 LITTLE RIVER TRIBAL WATER SYSTEM MANISTEE MI 49660 15 055294301 VINELAND ONAMIA MN 56359 16 055294502 PRAIRIE ISLAND WELCH MN 55089 17 055294503 LOWER SIOUX MORTON MN 56270 18 055294506 SIOUX TRAIL PRIOR LAKE MN 55372 19 055295003 SOUTH-CENTRAL WATER SYSTEM BOWLER WI 54416 20 055295310 Giiwedin Hayward WI 54843 21 055295401 LAC DU FLAMBEAU LAC DU FLAMBEAU WI 54538 22 055295508 KESHENA KESHENA WI 54135 23 055295703 ONEIDA #1 OR SITE #1 ONEIDA WI 54155 24 061020808 POTTAWATOMIE CO. -

The Voices of Children and Young People in Africa
REWIND RWD << 2003 - 2013 The Voices of 126 million contacts Children and Young People in Africa GIVING A VOICE TO CHILDREN AND YOUNG PEOPLE WORLDWIDE The Global Network of Child Helplines: African memberships as of April 2013 Current members in Africa - 30 members in 27 countries Associate members Full childhelpline members: 23 members in 23 countries Associate childhelpline members: 7 members in 5 countries • Childline Botswana Botswana • Association Mauritanienne de la Santé de la • Plan Benin (USHAHIDI) Benin • Direction Generale de L’Encadrement et de la Mère et de l’EnfantAMSME Mauritania • OCPM (L’Office Central de Protection des Protection d L’Enfant et de L’Adolescent • Halley Movement Mauritius Mineurs, de la famille et de la lutte contre la (Ministere de L’Action Sociale et de la Solidarite • Lihna Fala Crianca Mozambique traite des êtres humains) Benin Nationale) Burkina Faso • LifeLine/ChildLine Namibia Namibia • Defense for Children International (DCI) • Bureau International Catholique de l’Enfance • Human Development Intiatives - HDI Nigeria Cameroon Cameroon (BICE) - Cote d’Ivoire Cote d’Ivoire • Centre GINDDI Senegal • War Child UK (Tukinge Watoto) DRC • Enhancing Child Focused Activities - (ECFA) • Don Bosco Fambul Sierra Leone • War Child Holland DRC Ethiopia • Childline South Africa South Africa • Direction de la police Judiciaire (Brigade • Child and Environmental Development Association • Ministry of Education Toll-Free Line des Mœurs) Madagascar (CEDAG) Gambia Swaziland • Child Helpline Tanzania Tanzania • Association -
Finding and Repairing Leaks, Reducing Water Loss Are Critical to Water Systems, Large and Small
By Tony Kimmi, Technical Assistant Finding and Repairing Leaks, Reducing Water Loss are Critical to Water Systems, Large and Small s one of the “newer” Tech Assistants working at the downstream of the meter. Having elbows, valves and other Kansas Rural Water Association, I appreciate the fittings butted right next the meter can create turbulence in Aefforts that many others have made to help me become the water flow and therefore create inaccurate registration by more proficient with the work I do at the meter. KRWA for cities and rural water districts. Five examples of my work at Several KRWA staff members have spent What is frustrating is 30 years working for the Kansas KRWA in recent months Department of Health and Environment. that so many of the 1. One of the more interesting projects They know both the regulatory side and water systems have that I worked with in the last year was to they understand the small system side. been constructed help locate leakage from a water line in I'm not the “regulatory guy”. I appreciate the city of Fort Scott. We found a 2-inch the small system side of the equation and without there being any fire suppression line at Fort Scott I’m learning about the regulatory side. consideration for testing Community College leaking. Fire My sense is that while everyone can get master meters. suppression systems are not metered in hung up on “x” parts per million, if we Fort Scott. don’t keep the pipes together and make 2. Having given advice to the operator sure the leakages are stopped, there’s no in Effingham to exercise the valves, I water to test. -

These Companies and Utilities Support KRWA As Associate Members
These Companies and Utilities Support KRWA as Associate Members A1 Pump & Jet Services, Inc. Ford Meter Box, Inc. O'Keefe Law Office A. Y. McDonald Manufacturing Fort Bend Services, Inc. Olathe Winwater Works Company ACEC of Kansas Fortiline Waterworks Oral Health Kansas Aclara Technologies FTC Equipment, LLC P.B. Hoidale Co., Inc. Acord Cox & Company Gateway Industrial Power, Inc. Pittsburg Tank & Tower Maintenance Advanced Drainage Systems GDW Water Sampler Ponzer Youngquist AE2S Gelco Supply; dba RootX Preferred Tank & Tower Maintenance Alexander Pump & Services, Inc. Gerard Tank & Steel Inc. Division, Inc. Allgeier, Martin & Associates, Inc. GettingGreatRates.com PreLoad, LLC Alliance Pump & Mechanical Services, Inc Global Ecotechnologies, Inc. Professional Computer Solutions LLC American AVK Company GPM Enterprises, Inc. Professional Engineering Consultants American Flow Control Grasshopper Company Pumps of Oklahoma American States Utility Services Ground Water Associates Purple Wave Auction American Structures, Inc. Hall's Culligan Water R. E. Pedrotti Company, Inc. Aquafix, Inc. Hawkins, Inc Ranson Financial Group, LLC Axiom Instrumentation Services Haynes Equipment Co., Inc. Ray Lindsey Company B & B Electric Motor Company HK Solutions Group Raymond James Public Finance B & B Services HOA Solutions, Inc. Red Flint Sand and Gravel Baker Water Systems Hustler Turf Red Municipal & Industrial Equipment Co BARCO Municipal Products, Inc. Hydro Resources Mid Continent, Inc. Riley County Public Works Bartlett & West, Inc. Industrial Sales Company, Inc. RiverRoad Marketing, LLC Berry Tractor & Equipment Company Industrial Service and Supply, Inc. Romac Industries Inc. BG Consultants, Inc. Innovative Engineered Equipment RTS Water Solutions, Envocore Blue Nile Contractors Ixom Watercare Rural Water Impact / Municipal Impact BlueWater Solutions Group, Inc.