Confidence Intervals 415
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
CC9058-Compatibility
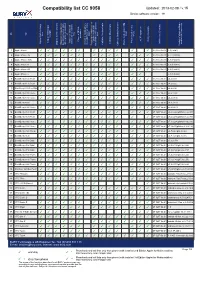
Compatibility list CC 9058 Updated: 2013-02-08 / v.15 Device software version: 19 on No key level keys Card Type tags) Phone strength activation A2DP supported Phone s REDIAL Charger available / private mode with Activation Bluetooth Phone book entries: Display: GSM-signal Call lists: Missed calls Article code (Charger) connection with device Display: Battery charge Bluetooth connection to used to test/ Comments after ignition is switched Access to mobile phone Call lists: Received calls voice-dial function (voice Phone book entries: SIM Display: Service provider the last connected phone Call lists: Dialled numbers Bluetooth device / phones Possibility to switch car kit Version of phone software 1 Apple iPhone ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 3.0(7a341) 2 Apple iPhone 3G ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 4.2.1 (8a306) 3 Apple iPhone 3GS ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 6.0 (10a403) 4 Apple iPhone 4 ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 6.0 (10a403) 5 Apple iPhone 4S ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 6.0 (10a403) 6 Apple iPhone 5 ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 6.1 (10b143) 7 BlackBerry 8100 Pearl ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0b.01 v4.5.0.69 8 BlackBerry 8110 Pearl ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0b.01 v4.5.0.55 9 BlackBerry 8220 Pearl Flip ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0a.01 v4.6.0.94 10 BlackBerry 8300 Curve ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0b.01 os 5.1.342 11 BlackBerry 8310 Curve ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0b.01 v4.5.0.180 12 BlackBerry 8800 ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0b.01 -

BURY Compatibility List Generator
Compatibility list CC 9068 Updated: Device software version: Box SW: 106Display SW: 140 on No call key level keys Card SMS Type Phone strength activation conference phone name SMS / Popup between calls A2DP supported Phone s REDIAL reject waiting call Charger available / private mode with Activation Bluetooth Phone book entries: Display: GSM-signal Multiparty call: Swap E-mail read Function Messages: Download Call lists: Missed calls Article code (Charger) connection with device Multiparty call: accept / Display: Battery charge Bluetooth connection to used to test/ Comments after ignition is switched Multiparty call: merge to Required default/factory Call lists: Received calls Multiparty call: hold on 1 Messages: Receive new Phone book entries: SIM Display: Service provider the last connected phone OPP: Synch. phone book Call lists: Dialled numbers Bluetooth device / phones Possibility to switch car kit Version of phone software 1 Apple iPhone ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 3.0 (7a341) 2 Apple iPhone 3G ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 4.2.1 (8c148) 3 Apple iPhone 3GS ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 6.0 (10a403) 4 Apple iPhone 4 ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 6.0 (10a403) 5 Apple iPhone 4S ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 6.0 (10a403) 6 BlackBerry 8110 Pearl ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0b.01 v4.5.0.55 7 BlackBerry 8220 Pearl Flip ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0a.01 v4.6.0.94 8 BlackBerry 8300 Curve ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ -
BURY Compatibility List Generator
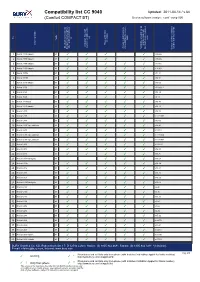
Compatibility list CC 9040 Updated: 2011-04-14 / v.64 (Comfort COMPACT BT) Device software version: comf_comp V05 on No key keys tags) Profile activation service provider Phone s REDIAL / private mode with Activation Bluetooth connection with device Bluetooth connection to used to test/ Comments after ignition is switched Access to mobile phone voice-dial function (voice the last connected phone Bluetooth device / phones Possibility to switch car kit Version of phone software 1 Nokia 2323 classic hf ✓ ✓ ✓ ✓ v 06.46 2 Nokia 2330 classic hf ✓ ✓ ✓ ✓ v 06.46 3 Nokia 2700 classic hf ✓ ✓ ✓ ✓ ✓ v 07.15 4 Nokia 2730 classic hf ✓ ✓ ✓ ✓ ✓ v 10.40 5 Nokia 3109c hf ✓ ✓ ✓ ✓ ✓ v07.21 6 Nokia 3110c hf ✓ ✓ ✓ ✓ ✓ v04.91 7 Nokia 3120 classic hf ✓ ✓ ✓ ✓ ✓ v10.00 8 Nokia 3230 hf ✓ ✓ ✓ ✓ ✓ v3.0505.2 9 Nokia 3250 hf ✓ ✓ ✓ ✓ ✓ v03.24 10 Nokia 3650 hf ✓ ✓ ✓ ✓ ✓ v4.13 11 Nokia 3710 fold hf ✓ ✓ ✓ ✓ ✓ v03.80 12 Nokia 3720 classic hf ✓ ✓ ✓ ✓ ✓ v09.10 13 Nokia 5200 hf ✓ ✓ ✓ ✓ ✓ v03.92 14 Nokia 5230 hf ✓ ✓ ✓ ✓ ✓ v 12.0.089 15 Nokia 5300 hf ✓ ✓ ✓ ✓ ✓ v05.00 16 Nokia 5310 XpressMusic hf ✓ ✓ ✓ ✓ ✓ v09.42 17 Nokia 5500 hf ✓ ✓ ✓ ✓ ✓ v 03.18 18 Nokia 5530 XpressMusic hf ✓ ✓ ✓ ✓ ✓ v 11.0.054 19 Nokia 5630 XpressMusic hf ✓ ✓ ✓ ✓ ✓ v 012.008 20 Nokia 5700 hf ✓ ✓ ✓ ✓ ✓ v 03.83.1 21 Nokia 6103 hf ✓ ✓ ✓ ✓ ✓ v04.90 22 Nokia 6021 hf ✓ ✓ ✓ ✓ ✓ v03.87 23 Nokia 6110 Navigator hf ✓ ✓ ✓ v03.58 24 Nokia 6124c hf ✓ ✓ ✓ ✓ ✓ v04.34 25 Nokia 6125 hf ✓ ✓ ✓ ✓ ✓ v03.71 26 Nokia 6131 hf ✓ ✓ ✓ ✓ v03.70 27 Nokia 6151 hf ✓ ✓ ✓ ✓ ✓ v03.56 28 Nokia 6210 Navigator hf ✓ ✓ ✓ ✓ ✓ v03.08 29 Nokia 6230 hf ✓ ✓ ✓ ✓ ✓ v5.40 30 Nokia 6230i hf ✓ ✓ ✓ ✓ ✓ v3.30 31 Nokia 6233 hf ✓ ✓ ✓ ✓ ✓ v03.70 32 Nokia 6234 hf ✓ ✓ ✓ ✓ ✓ v3.50 33 Nokia 6270 hf ✓ ✓ ✓ ✓ ✓ v3.66 34 Nokia 6280 hf ✓ ✓ ✓ ✓ ✓ v4.25 35 Nokia 6288 hf ✓ ✓ ✓ ✓ ✓ v05.92 36 Nokia 6300 hf ✓ ✓ ✓ ✓ ✓ v 04.70 37 Nokia 6300i hf ✓ ✓ ✓ ✓ ✓ v03.41 38 Nokia 6301 hf ✓ ✓ ✓ ✓ ✓ v 04.61 39 Nokia 6303 classic hf ✓ ✓ ✓ ✓ ✓ v 08.90 40 Nokia 6303i classic hf ✓ ✓ ✓ ✓ ✓ v 07.10 BURY GmbH & Co. -

Compatibility List CC 9048 Device Software Version: 22
Updated: 2016-10-25 / V.22 Compatibility list CC 9048 Device software version: 22 No Type A2DP activation (Charger) supported device key Article code car kit / private connection with test/ Comments phone voice-dial software used to Phone‘s REDIAL Phone‘s REDIAL Version of phone Version Access to mobile Charger available Possibility to switch Activation Bluetooth function (voice tags) mode with Bluetooth device / phones keys 1 Apple iPhone 0-07-0258-0.07 3.0(7A341) 2 Apple iPhone 3G 0-07-0258-0.07 4.2.1 (8A306) 3 Apple iPhone 3GS 0-07-0258-0.07 6.1.2 (10B146) 4 Apple iPhone 4 0-07-0258-0.07 7.0.2 (11A501) 5 Apple iPhone 4S 0-07-0258-0.07 7.0.4 (11B554a) 6 Apple iPhone 5 0-07-0258-0.08 10.0.2 (14A456) 7 Apple iPhone 5c 0-07-0258-0.08 10.0.2 (14A456) 8 Apple iPhone 5s 0-07-0258-0.08 10.0.2 (14A456) 9 Apple iPhone 6 0-07-0258-0.08 10.0.2 (14A456) 10 Apple iPhone 6s 0-07-0258-0.08 10.0.2 (14A456) 11 Apple iPhone 6 Plus 0-07-0258-0.08 10.0.2 (14A456) 12 Apple iPhone 6s Plus 0-07-0258-0.08 10.0.2 (14A456) 13 Apple iPhone 7 0-07-0258-0.08 10.0.3 (14A551) 14 Apple iPhone 7 Plus 0-07-0258-0.08 10.0.3 (14A551) 15 Apple iPhone SE 0-07-0258-0.08 10.0.2 (14A456) 16 ASUS Solaris 0-07-0258-0.02 V4.2.2 WWE 17 BlackBerry 8100 Pearl 0-07-0258-0.02 V4.5.0.69 18 BlackBerry 8110 Pearl 0-07-0258-0.02 V4.5.0.55 19 BlackBerry 8220 Pearl Flip 0-07-0258-0.01 V4.6.0.94 20 BlackBerry 8300 Curve 0-07-0258-0.02 V4.5.0.182 21 BlackBerry 8310 Curve -

Devices for Which We Currently Recommend Opera Mini 7.0 Number of Device Models
Devices for which we currently recommend Opera Mini 7.0 Number of device models: 625 Platforms included: JME, BlackBerry, Android, S60 and iOS List generated date: 2012-05-30 -------------------------------------------------------------------------------------------------------------------------------------- au by KDDI IS03 by Sharp BlackBerry 9900 Bold Acer beTouch E110 au by KDDI REGZA Phone BlackBerry Curve 3G 9300 IS04 by Fujitsu-Toshiba Acer beTouch E130 Dell Aero au by KDDI Sirius IS06 by Acer Iconia Tab A500 Pantech Dell Streak Acer Liquid E Ezze S1 Beyond B818 Acer Liquid mt Fly MC160 BlackBerry 8520 Curve Acer Liquid S100 Garmin-Asus nüvifone A10 BlackBerry 8530 Curve Acer Stream Google Android Dev Phone BlackBerry 8800 1 G1 Alcatel One Touch OT-890D BlackBerry 8820 Google Nexus One Alfatel H200 BlackBerry 8830 Google Nexus S i9023 Amoi WP-S1 Skypephone BlackBerry 8900 Curve HTC A6277 Apple iPad BlackBerry 9000 Bold HTC Aria A6366 Apple iPhone BlackBerry 9105 Pearl HTC ChaCha / Status / Apple iPhone 3G BlackBerry 9300 Curve A810e Apple iPhone 3GS BlackBerry 9500 Storm HTC Desire Apple iPhone 4 BlackBerry 9530 Storm HTC Desire HD Apple iPod Touch BlackBerry 9550 Storm2 HTC Desire S Archos 101 Internet Tablet BlackBerry 9630 Tour HTC Desire Z Archos 32 Internet Tablet BlackBerry 9700 Bold HTC Dream Archos 70 Internet Tablet BlackBerry 9800 Torch HTC Droid Eris Asus EeePad Transformer BlackBerry 9860 Torch HTC Droid Incredible TF101 ADR6300 HTC EVO 3D X515 INQ INQ1 LG GU230 HTC EVO 4G Karbonn K25 LG GW300 Etna 2 / Gossip HTC Explorer -
Oxygen Forensic Suite
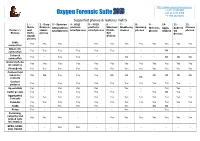
http://www.oxygen-forensic.com +1 877 9 OXYGEN Oxygen Forensic Suite +44 20 8133 8450 +7 495 222 9278 Supported phones & features matrix 1 – 2 - Sony 3 – Symbian 4 - UIQ2 5 – UIQ3 6 - 7 - 8- 9- 10- 11- 12- Nokia Ericsson S60 platform platform platform Windows Blackberry Samsung Motorola Apple Android Chinese Feature \ and classic smartphones smartphones smartphones Mobile devices phones phones devices OS phones Phones Vertu phones 5/6 devices classic devices phones Cable Yes Yes Yes - Yes Yes Yes Yes Yes Yes Yes Yes connection Bluetooth Yes Yes Yes Yes Yes Yes - - - NA - - connection Infrared Yes - Yes Yes - - NA - - NA NA NA connection General phone Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes information Phonebook Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Custom field labels for NA NA Yes Yes Yes NA NA NA NA NA NA contacts NA Contact Yes - Yes Yes Yes Yes Yes Yes Yes Yes Yes - pictures Speed dials Yes - Yes Yes Yes - Yes - - Yes Yes - Caller groups Yes - Yes Yes Yes Yes - - Yes NA Yes - Aggregated Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Contacts Calendar Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Tasks Yes - Yes Yes Yes - Yes - NA NA - - Notes Yes - - - - - Yes - - Yes - - Incoming, outgoing and Yes Yes Yes - - Yes Yes Yes Yes Yes Yes Yes missed calls information GPRS, EDGE, - - Yes Yes - - - - - - - CSD, HSCSD - and Wi-Fi traffic and sessions log Sent and received SMS, - Sent SMS - Yes Yes Yes(2) - - - - - - MMS, E-mail messages log Deleted - messages - - Yes(1) - Yes(1) - - - Yes(8) - - information Flash SMS -

Motorola Razr2 V8 User Manual
Guidebooks Motorola razr2 v8 user manual Motorola razr2 v8 user manual . Download: Motorola razr2 v8 user manual and user guide is also related with Motorola Razr2 V9 Service Manual, include : Motorola Razr2. V9x Manual, Motorola Razr2 V8 Manual, Motorola Razr2 V9m. Motorola RAZR2 V8 Manual Online: Return A Call, Caller Id. Motorola RAZR V8 / User Manual - Page 4. Introducing your new MOTORAZR2 V8 GSM wireless phone. Heres a quick anatomy lesson. Charge Indicator Light. Read Online and Download PDF Ebook motorola razr xt912 user manual. PDF Ebook styles motorola razr2 v8 user manual, Discover unlimited ebooks. This MOTO RAZR2 V8 is a new factory refurbished model. bx41, motorola charger and motorola General user manual with motorola refurbish packing box. You can download the file by clicking the following link razr v3c user manual flip for motorola v3 v3c v3i v3m v3t v8 v9 w490 w755 samsung: a900 d820 d807. Motorola Fv700 User Manual from our library is free resource for public. Motorola Fv700 User Manual is available through our online libraries and we offer online MOTOROLA V8 USER MANUAL MOTOROLA RAZR2 V9 USER MANUAL. We have ebooks for every subject motorola razr xt912 user manual, Discover unlimited ebooks from our database related with motorola razr2 v8 user manual. Motorola RAZR2 V8 Unlocked Phone with 2 MP Camera, and MP3/Video charger, mini-to-micro USB adapter, Quick Start Guide and User Manual They sent a Motorola RAZR2 V9x Black Phone, an original American supported (AT&T). and user guide is also related with Motorola Razr2 V9 Service Manual, include : Motorola Razr2. -

Samsung OMNIA, Iphone 3G
APPENDIX A 8 iPhone Killer Alternatives : iPhone Killer Page 1 of 7 iPhone Killer Most comprehensive iPhone Killer information site z Home z About iPhone Killer z Advertise z Ringtones z Sitemap 8 iPhone Killer Alternatives By admin on Jul 21, 2008 in Blackberry Bold 9000, Garmin Nuvifone, HTC Touch Pro, LG Dare, LG Voyager, Nokia N96, Samsung Instinct, Samsung OMNIA, iPhone 3G Information Week has list of 8 iPhone Killers that are alternatives to the iPhone 3G. Their list goes like this 1. Blackberry Bold 2. HTC Touch Pro 3. LG Voyager 4. LG Dare 5. Nokia N96 6. Samsung OMNIA 7. Samsung Instinct 8. Garmin Nuvifone All of these phones can be found on this website for additional information and we even have many of the phones they don’t know about. The original post can be read here. ShareThis Post a Comment Name (required) http://www.iphonekiller.com/2008/07/21/8-iphone-killer-alternatives/ 1/29/2009 Nokia 5800 ExpressMusic reaches 1M shipments : iPhone Killer http://www.iphonekiller.com/2009/01/24/nokia-5800-expressmusic-reach... iPhone Killer Most comprehensive iPhone Killer information site Home About iPhone Killer Advertise Ringtones Sitemap Nokia 5800 ExpressMusic reaches 1M shipments By admin on Jan 24, 2009 in Nokia 5800 1 of 7 1/28/2009 1:32 PM Nokia 5800 ExpressMusic reaches 1M shipments : iPhone Killer http://www.iphonekiller.com/2009/01/24/nokia-5800-expressmusic-reach... Who would’ve thought that this first iPhone Killer from Nokia has already reached 1M shipment in just few short months? The original iPhone took almost a year before it had 1M shipment. -
Sprint Buyback Program
Discover Sprint Find a store Shopping Cart Search Home Program Overview FAQs Eligible Devices Check Status Support En Español Sprint Buyback Program Eligible Devices This page displays the current list of devices eligible for a credit with the Sprint Buyback Program. If your device is not listed consider recycling it with Sprint Project ConnectSM to help fund Internet safety for kids. Manufacturer Model Trade In Acer 6120 Iconia $200.00 Acer A100 Iconia Tab $70.00 Acer A200 Iconia Tab $70.00 Acer A500 Iconia Tab $80.00 Acer A510 Iconia Tab $75.00 Acer A700 Iconia Tab $72.00 Acer AO531H Aspire One $16.00 Acer AOD255 Aspire One $11.00 Acer Aspire One 722 $35.00 Acer Aspire One 725 $35.00 Acer Aspire One 756 $35.00 Acer Aspire One D270 $35.00 Acer E100 beTouch $5.00 Acer Iconia Tab A501 $10.00 Acer S300 Iconia Smart $100.00 Acer W500 Iconia Tab $92.00 Acer W500P Iconia Tab $92.00 Ainol Novo 7 Advanced II $40.00 Ainol Novo 7 Aurora $40.00 Ainol Novo 7 Aurora II $40.00 Ainol Novo 7 Elf $40.00 Ainol Novo 7 Elf 2 $40.00 Ainol Novo 7 Fire $40.00 Ainol Novo 7 Flame $40.00 Ainol Novo 7 Mars $40.00 Ainol Novo 7 Mars Slate $40.00 Ainol Novo 7 Paladin $40.00 Ainol Novo 7 Tornado $40.00 Alcatel OT-960C One Touch Ultra $40.00 Alcatel OT-T10 One Touch T10 $40.00 Alcatel OT-T20 One Touch T20 $40.00 Alcatel OT-T60 One Touch T60 $40.00 Apple A1432 iPad Mini 16GB - WiFi $149.00 Apple A1432 iPad Mini 32GB - WiFi $185.00 Apple A1432 iPad Mini 64GB - WiFi $227.00 Apple A1454 iPad Mini 16GB - ATT $189.00 Apple A1454 iPad Mini 32GB - ATT $225.00 Apple A1454 iPad -

These Devices Are Supported on the Latest Version of Firmware. Please Ensure You Are Running the Most Recent Firmware to Ensure Device Compatibility
These devices are supported on the latest version of firmware. Please ensure you are running the most recent firmware to ensure device compatibility. Updated 3/8/2010 (Contact us or vist http://www.cradlepoint.com for latest compatibility list) 3 (UK) Huawei E156G Alltel Franklin CDU550 Huawei EC168/C Huawei EC228 Pantech UM175 UTStarcom UM150 (Pantech UM150) AT&T Option QuickSilver Sierra Wireless 881U Sierra Wireless 875U USBConnect 881 USBConnect Mercury USBConnect Lightning ZTE MF636 Option GT Max 3.6 Express Option GT Ultra Express Blackberry 8310 (Curve) Blackberry 9000 (Bold) HP iPaq 910 Motorola RAZR v3xx Motorola Q v9h Samsung Blackjack Samsung SGHA707 BMobile (Japan) ZTE MF626 Bell (Canada) Novatel Wireless U760 BridgeMAXX WiMAX ZTE TU25 Clear 4G When using the Clear WiMAX network, the following Modem Firmware must be loaded onto the CradlePoint Router. Download Modem Firmware 5.2.206 Clear USB Modem Clear USB 4G Modem Franklin U300 (3G and 4G) Comcast HighSpeed2Go When using the Comcast HighSpeed2Go network, the following Modem Firmware must be loaded onto the CradlePoint Router Download Modem Firmware 5.2.206 Franklin CMU300 (3G and 4G) ZTE TU25 Cricket Calcomp a600 Pantech UM100 Pantech UMW185 EMobile (Japan) D02HW D11LC D12LC D21HW D21LC D22HW nTelos Franklin CDU680 Kyocera KPC680 NTT Docomo (Japan) LG L02A O2 (UK) Sierra Wirless Compass 889U Orange (UK) Huawei E160E Pioneer Cellular Franklin CDU680 Sierra Wireless USB 598 Sierra Wireless Aircard 402 Rogers (Canada) Novatel MC950D ZTE MF636 (Rocket Stick) ZTE MF668 (Rocket Stick) Novatel X950D Softbank (Japan) Softbank C01LC Generic UMTS/GSM Devices These devices were tested using the AT&T network in the United States and may or may not work with other UMTS/GSM carriers internationally. -

BURY Compatibility List Generator
Compatibility list CC 9048 Updated: 2013-09-24 / v.22 Device software version: 20 No key keys Type tags) activation A2DP supported Phone s REDIAL Charger available / private mode with Activation Bluetooth Article code (Charger) connection with device used to test/ Comments Access to mobile phone voice-dial function (voice Bluetooth device / phones Possibility to switch car kit Version of phone software 1 Apple iPhone ✓ ✓ ✓ ✓ 07-0257-0c.01 3.0(7a341) 2 Apple iPhone 3G ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 4.2.1 (8a306) 3 Apple iPhone 3GS ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 6.1.2 (10b146) 4 Apple iPhone 4 ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 6.0.1 (10a523) 5 Apple iPhone 4S ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0c.01 6.0.1 (10a523) 6 Apple iPhone 5 ✓ ✓ ✓ ✓ ✓ ✓ 04-29-0020-0 7.0 (11a465) 7 ASUS Solaris ✓ ✓ ✓ ✓ 07-0257-0b.01 v4.2.2 wwe 8 BlackBerry 8100 Pearl ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0b.01 v4.5.0.69 9 BlackBerry 8110 Pearl ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0b.01 v4.5.0.55 10 BlackBerry 8220 Pearl Flip ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0a.01 v4.6.0.94 11 BlackBerry 8300 Curve ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0b.01 v4.5.0.182 12 BlackBerry 8310 Curve ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0b.01 v4.5.0.180 13 BlackBerry 8520 Curve ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0a.01 v4.6.1.286 14 BlackBerry 8800 ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0b.01 v4.5.0.174 15 BlackBerry 8900 Curve ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0a.01 v5.0.0.411 16 BlackBerry 9000 Bold ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0a.01 v4.6.0.40(platform 4.0.0.82) 17 BlackBerry 9100 Pearl ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0a.01 v5.0.0.696(platform 6.2.0.57) 18 BlackBerry 9105 Pearl ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0a.01 v5.0.0.696(platform 6.2.0.57) 19 BlackBerry 9320 Curve ✓ ✓ ✓ ✓ ✓ ✓ 07-0257-0a.01 -
Seznam Zařízení, Která Podporují Pouze 2G a 3G Síť (Po Vypnutí 3G Budou Nadále Fungovat, Ale Pomaleji)
Seznam zařízení, která podporují pouze 2G a 3G síť (po vypnutí 3G budou nadále fungovat, ale pomaleji) Acer F900 JK808,JK900,DM550,Crown Nokia E63-1 Samsung GT-S5550 Acer Iconia Tab Jeko iGet Blackview JK890,JK600,JK606,JK450 Nokia E65 Samsung GT-S5600 Acer Iconia Tab A1-811 Jeko iGet Blackview Ultra,Zeta,Alife Nokia E66 Samsung GT-S5600V Acer Liquid E3 P1,Breeze Nokia E66-1 Samsung GT-S5610 Acer Liquid E700 (E39) JSR Innos D10 Nokia E7-00 (RM-626) Samsung GT-S5611 Acer Liquid Jade (S55) JSR Innos D9 Nokia E71-1 Samsung GT-S5611V Acer Liquid M220 JSR Innos i2 Nokia E71-2 Samsung GT-S5620 Acer Liquid Z200,Z205 JSR Innos i3 Nokia E71-3 Samsung GT-S7220 Acer Liquid Z220 JSR Innos i6 Nokia E72-1,E72i (RM-530) Samsung GT-S7230E Acer Liquid Z4 Karasnn Zopo ZP580,700,780,998,1000 Nokia E72-2 (RM-529) Samsung GT-S7350i Acer Liquid Z500 Karasnn ZOPO ZP980,ZP1000 Nokia E75 Samsung GT-S7550 Acer Liquid Z520 KC Mobile 814 Nokia E90 Samsung GT-S8000 Acer Liquid Z5 (Z150) KC Mobile KC 1000 Nokia Lumia 520 (RM-914) Samsung GT-S8500 Acer Liquid Zest (T06) KVD Doogee Nokia Lumia 530 Dual SIM (RM-1019) Samsung GT-Y3300 Acer S100 DG350,DG2014,DG550,DG800,DG330 Nokia Lumia 530 (RM-1017) Samsung i8510 Acer S120 KVD Doogee S40 Lite Nokia Lumia 620 (RM-846) Samsung M7500 ACT L eWON KVD Doogee T3 Nokia Lumia 630 Dual SIM (RM-978) Samsung Nexus S (GT-I902x) Adart Aligator S4090 Duo KVD Doogee Voyager2 DG310,Kissme Nokia Lumia 630 (RM-976) Samsung Omnia 7 Adart Aligator S5070 Duo DG580,Titans2 DG700,L Nokia Lumia 720 (RM-885) Samsung S7350 Adart Aligator S5520