Self-Force and Green Function in Schwarzschild Spacetime Via Quasinormal Modes and Branch Cut
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
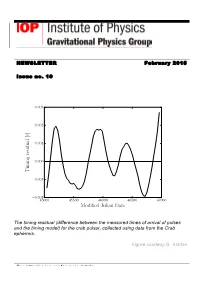
Modified Julian Date Timing Residual
NEWSLETTER February 2015 Issue no. 10 0.003 0.002 0.001 0.000 Timing residual [s] 0.001 − 0.002 − 45000 45500 46000 46500 47000 Modified Julian Date The timing residual (difference between the measured times of arrival of pulses and the timing model) for the crab pulsar, collected using data from the Crab ephermis. Figure courtesy G. Ashton See http://gp.iop.org for more details Gravitational Physics Group February 2015 Table of Contents Welcome from the Chair .................................................... 3 Events ................................................................................ 5 Young Theorists’ Forum 2013 ......................................................................... 5 New Frontiers in Dynamical Gravity ............................................................... 5 BritGrav 2014 .................................................................................................... 6 Prizes ................................................................................. 8 2014 GPG Thesis Prize .................................................................................... 8 Contributed Articles ........................................................... 9 The effect of timing noise on continuous gravitational wave searches ..... 9 Black holes and scalar hair ........................................................................... 17 Untangling precession: Modelling the gravitational wave signal from precessing black hole binaries .................................................................... -

Curriculum Vitae
Christopher Berry Personal Department Address Email Telephone Information School of Physics & Astronomy [email protected] +44 (0) 1214 146541 University of Birmingham Edgbaston Website Twitter Birmingham cplberry.com @cplberry B15 2TT Education University of Birmingham September 2014 { April 2015 PGCert (Associate Module) Foundation of Learning & Teaching in Higher Education Institute of Astronomy, University of Cambridge October 2009 { August 2013 PhD in Astronomy Supervisor: Jonathan Gair Exploring gravity with strong-field tests and gravitational waves. Theoretical study of what can be learned about astrophysical systems and the nature of gravity from gravitational probes, in particular gravitational waves. Funded by STFC and the Cambridge Philosophical Society. Churchill College, University of Cambridge October 2005 { July 2009 BA (Hons), MSci Natural Sciences Part III Experimental & Theoretical Physics 1st Part II Experimental & Theoretical Physics 1st Part IB Physics, Advanced Physics, Mathematics 1st Part IA Physics, Materials & Mineral Science, Geology, Mathematics 1st Worcester College of Technology September 2004 { June 2005 Certificate in Management (Level 3) Distinction Introductory Certificate in Management (Level 3) Distinction Droitwich Spa High School & Sixth Form Centre September 1998 { June 2004 STEP Mathematics II, Mathematics III 1 A-level Physics, Maths, Further Maths, General Studies A AS-level Geography A GCSE 10 (including Maths, English and French) 9 A*s, 1 A Honours, Awards 2018 IOP Astroparticle Physics Early -

J CQG BK 0315 Highlights-A4-4.Indd
INVITED Strings, branes, supergravity Constraining conformal field ARTICLE theories with a slightly broken Classical and and gauge theory higher spin symmetry Juan Maldacena and Alexander Zhiboedov FTC Quantum Gravity Quantum supersymmetric cosmology 2013 Class. Quantum Grav. 30 104003 and its hidden Kac-Moody structure “Determines the leading form of the correlation functions in the CFT dual for a large class of higher spin theories, using only very general properties of the T Damour and P Spindel theory. The resulting form of the correlation functions is highly constrained. Highlights of 2013–2014 2013 Class. Quantum Grav. 30 162001 These universal results will likely play an important part in the development of “This is a an elegant paper, where ingredients such as supersymmetry, group holographic duality for higher spin.” Comment from Editorial Board theory, fundamental physics, the early universe and lateral comments to other areas come together in a highly technical article that is brief but very Welcome to the 2015 CQG Highlights brochure, featuring some of the best papers informative. This work shows how quantum cosmology without supersymmetry cannot be ignored.” Comment from Editorial Board Holography without strings? published during the last 12 months, as selected by our Editorial Board. 14% Donald3.6 Marolf As the centenary of Albert Einstein’s discovery of general relativity, 2015 will be an 2014 Class. Quantum Grav. 31 015008 exciting year for the CQG community. To mark this occasion, CQG will publish a special 12% TOPICAL Double field theory: REVIEW “Emphasizes the role of the gravitational Gauus law constraint and issue of the journal entitled ‘Milestones of General Relativity’, which will review some of a pedagogical review entanglement3.4 in the bulk in holography. -

Tidal Invariants for Compact Binaries on Quasi-Circular Orbits
Tidal invariants for compact binaries on quasi-circular orbits Sam R. Dolan,1, ∗ Patrick Nolan,2 Adrian C. Ottewill,2 Niels Warburton,2 and Barry Wardell3 1Consortium for Fundamental Physics, School of Mathematics and Statistics, University of Sheffield, Hicks Building, Hounsfield Road, Sheffield S3 7RH, United Kingdom. 2School of Mathematical Sciences and Complex & Adaptive Systems Laboratory, University College Dublin, Belfield, Dublin 4, Ireland. 3Department of Astronomy, Cornell University, Ithaca, NY 14853, USA. (Dated: September 20, 2018) We extend the gravitational self-force approach to encompass `self-interaction' tidal effects for a compact body of mass µ on a quasi-circular orbit around a black hole of mass M µ. Specifically, we define and calculate at O(µ) (conservative) shifts in the eigenvalues of the electric- and magnetic-type tidal tensors, and a (dissipative) shift in a scalar product between their eigenbases. This approach yields four gauge-invariant functions, from which one may construct other tidal quantities such as the curvature scalars and the speciality index. First, we analyze the general case of a geodesic in a regular perturbed vacuum spacetime admitting a helical Killing vector and a reflection symmetry. Next, we specialize to focus on circular orbits in the equatorial plane of Kerr spacetime at O(µ). We present accurate numerical results for the Schwarzschild case for orbital radii up to the light-ring, calculated via independent implementations in Lorenz and Regge-Wheeler gauges. We show that our results are consistent with leading-order post-Newtonian expansions, and demonstrate the existence of additional structure in the strong-field regime. We anticipate that our strong-field results will inform (e.g.) effective one-body models for the gravitational two-body problem that are invaluable in the ongoing search for gravitational waves. -

Procedura Di Valutazione Comparativa Per La Stipula Di N
PROCEDURA DI VALUTAZIONE COMPARATIVA PER LA STIPULA DI N. 1 CONTRATTI DI LAVORO SUBORDINATO PER RICERCATORE A TEMPO DETERMINATO, AI SENSI DELL’ART. 24, COMMA 3, LETT. B) DELLA LEGGE N. 240 DEL 30 DICEMBRE 2010 PER IL S.C. 02/A2 PROFILO RICHIESTO S.S.D. FIS/02 — FISICA TEORICA MODELLI E METODI MATEMATICI — DIPARTIMENTO DI SCIENZE MATEMATICHE E INFORMATICHE, SCIENZE FISICHE E SCIENZE DELLA TERRA DELLA UNIVERSITÀ DEGLI STUDI DI MESSINA VERBALE N. 2 (Valutazione preliminare dei candidati e ammissione alla discussione pubblica) L’anno 2021 il giorno 9 del mese di Marzo alle ore 9:00 si riunisce al completo, per via telematica, ognuno nella propria sede universitaria, come previsto dall’art. 9 comma 8 del Regolamento d’Ateneo, la Commissione giudicatrice, della valutazione comparativa in epigrafe, nominata con D.R. prot. n. 6602 del 19 gennaio 2021, pubblicato sul sito internet dell’Università di Messina, per procedere alla valutazione dei titoli, dei curricola e della produzione scientiGica dei candidati. Sono presenti i sotto elencati commissari: Prof. Antonio Davide POLOSA Università degli Studi di Roma, `La Sapienza’ (Presidente) Prof. Giovanni DE LELLIS Università degli Studi di Napoli `Federico II’ (Componente) Prof. Massimo MASERA Università degli Studi di Torino (Segretario) Il presidente della commissione comunica che sono trascorsi i 7 giorni richiesti dalla pubblicazione dei criteri e che la Commissione può leggittimamente proseguire i lavori. I componenti accedono, tramite le proprie credenziali, alla piattaforma informatica https://istanze.unime.it -

Gregory Ashton October 2019
Dr Gregory Ashton October 2019 Address School of Physics & Astronomy, Contact +61 0452053330 Monash University, Email [email protected] Clayton, 3800, VIC, AU Website greg-ashton.physics.monash.edu Personal profile I am an aspiring leader in gravitational wave data analysis and astrophysical inference and have consistently published high impact work across these fields. I am the senior core developer of the second-generation gravitational wave inference package Bilby, which has been selected, amongst many strong alternatives, to be the flagship astrophysical inference code for the LIGO and the Virgo Scientific Collaboration. All future astrophysical discoveries from future gravitational wave detections will be made using Bilby. I am the chair of the international Bilby development team and have extensive experience in software development and deployment. I have been the subject of international news coverage for work published in Nature Astronomy, providing new insights into understanding neutron stars using radio pulsars glitches. I am on the paper writing team for GW190425, the second binary neutron star inspiral observed by LIGO & Virgo. Education 2012-2016 PhD in Mathematics, University of Southampton (GB) and Albert Einstein Institute (Han- nover, DE). Awarded 29th July 2016. 2008-2012 MPhys, 1st class (Hons), University of Southampton (GB). 2006-2008 General Certificate of Education Advanced Level, in Physics, Mathematics, and Music (AAC), Ferndown Upper School Sixth Form (GB). Academic Experience 2018-2021 Assistant Lecturer: 3-year fixed term postdoctoral researcher, School of Physics and Astron- omy, Monash University, (Melbourne, AU). 2016-2018 Wissenshaftler (Scientist): 2-year fixed term postdoctoral researcher, Albert Einstein Insti- tute (Hannover, DE). -

Britgrav 14 Abstracts
BritGrav 14 Abstracts Martin Hewitson Albert Einstein Institute, Hannover LISA Pathfinder - A mission status report LISA Pathfinder (LPF) is a precursor and technology validation mission for LISA-like Gravitational Wave Observatories in space. Some of the key technology needed for these observatories, such as micro-Newton propulsion, space-based optical metrology, drag-free control, and inertial sensing, will be directly tested on LPF. With a scheduled launch date of July 2015, the mission is at an advanced stage of integration and testing. This talk will give an overview of the overall mission, giving the status of the various key components, a discussion on the key noise sources, and a brief introduction to the experiments that will be carried out during mission operations. Carl-Johan Haster University of Birmingham Validation of approximate mass measurement prediction against Bayesian results. The gravitational wave signal from a coalescing compact binary encodes information about the parameters of the binary, where its mass and spin parameters are of particular astrophysical interest. We compare both existing and new approximate methods for predicting the accuracy with which mass parameters can be recovered against a fully coherent Bayesian inference analysis, evaluating their relative regions of validity, both in terms of recovered parameter accuracy and computational effort required. Gregory Ashton Universty of Southampton Gravitational wave searches from noisy neutron stars Neutron stars provide a fruitful laboratory for fundamental physics, their potential as gravitational wave emitters makes them a prime candidate for detectors in Advanced LIGO. The timing model used by observers to track the phase of pulses, electromagnetic emmisions from neutron stars, are limited to a few terms in a Taylor expansion. -
![Color1claudia De Rham – Professor [-20Pt] Imperial College London Physics Department, Theoretical Physics Group](https://docslib.b-cdn.net/cover/2027/color1claudia-de-rham-professor-20pt-imperial-college-london-physics-department-theoretical-physics-group-2722027.webp)
Color1claudia De Rham – Professor [-20Pt] Imperial College London Physics Department, Theoretical Physics Group
Claudia de Rham Imperial College London Professor Physics Department, Theoretical Physics Group Research Interests My expertise lies at the interface between Gravity, Cosmology and Particle Physics where I develop and test new models and paradigms. I apply field theory techniques to gravity and cosmology to tackle some of the outstanding open questions in physics from the nature of gravity, its embedding in a consistent high energy completion, the origin and evolution of our Universe and the late-time acceleration of the Universe. Current Appointments Since 2018 Imperial College London, Theoretical Physics group, London, UK, Professor. Since 2018 Perimeter Institute for Theoretical Physics, ON, Canada, Simons Emmy Noether Visiting Fellow. Since 2019 Case Western Reserve University, OH, USA, Adjunct Professor of Physics. Past Academic Positions 2016 – 2018 Imperial College London, Theoretical Physics group, London, UK, Reader. 2017 – 2019 Case Western Reserve University, OH, USA, Adjunct Associate Professor of Physics. 2011 – 2016 Case Western Reserve University, Department of Physics, Cleveland, OH, USA, Assistant Professor, (tenure–track) then Associate Professor, (tenured). 2010 – 2011 Geneva University, Department of Theoretical Physics, Geneva, Switzerland, SNSF Assistant Professor. 2006 – 2009 McMaster University, Hamilton, Canada. & Perimeter Institute for Theoretical Physics, Waterloo, Canada. Joint postdoctoral position in Cosmology. 2005 – 2006 McGill University, Physics Department, Montreal, Canada. Postdoctoral position in Cosmology. Education and Training 2002 – 2005 PhD from DAMTP, Cambridge University, UK. PhD Advisor: Prof. Anne-Christine Davis. 1998 – 2000 MSc, Ecole Polytechnique of Paris, France. 1996 – 2001 MSc, physics at EPFL, Ecole Polytechnique of Lausanne, Switzerland. Grants & Fundings 2020 – 2025 Named as 2020 Simons Foundation Investigator. 2020 – 2023 Co-I on STFC Group Grant, PI: Prof. -

CV of Prof. Dr. Muhammad Sharif
Prof. Dr. Muhammad Sharif (TI) Distinguished National Professor CURRICULUM VITAE NAME: MUHAMMAD SHARIF (T.I.) FATHER'S NAME: JUMMAH KHAN NATIONALITY: PAKISTANI ADDRESS: DEPARTMENT OF MATHEMATICS, UNIVERSITY OF THE PUNJAB, LAHORE-54590, PAKISTAN PHONE: + 92 42 99232026, +92 3334231696 E_MAIL ADDRESS: [email protected], [email protected] URL: http://faculty.m-sharif.pu.edu.pk/ https://en.wikipedia.org/wiki/Muhammad_Sharif_(cosmologist) RESEARCH SUMMARY Civil Award: Tamgha-i-Imtiaz Total Research papers in Impact Factor journals: 588 Cumulative IF: 1419 Cumulative citations: 12500 h-index: 50 i10-index: 362 ORCID ID: https://orcid.org/0000-0001-6845-3506 Among World's Top 2% researchers in Stanford University’s list (2020) Lectures delivered in Local/International Conferences: 113 PhD Supervised: 28 PhD in Progress: 05 MPhil Supervised: 75 MPhil in Progress: 07 A complete list of research papers can be seen at the following link. http://pu.edu.pk/images/publication/1408596083423-Pub.pdf I. ACADEMIC QUALIFICATIONS Degree Date Institutions Subject(s) BSc Nov. 1983 Islamia University Maths A, B Courses Bahawalpur and Physics MSc Dec. 1985 Quaid-i-Azam Applied Mathematics University Islamabad MPhil Nov. 1987 -do- Applied Mathematics PhD Dec. 1991 -do- Applied Mathematics (Relativity) II. FIELDS OF INTEREST Gravitational Theory, Astrophysics and Cosmology 15/07/2021 1 Prof. Dr. Muhammad Sharif (TI) Distinguished National Professor III. EXPERIENCE A. ACADEMIC EXPERIENCE: 1. Tenured Professor at Department of Mathematics, University of the Punjab, Lahore from December 21, 2012 to to-date. 2. Professor (TTS) at Department of Mathematics, University of the Punjab, Lahore from April 28, 2008 to to-date. -

LIGO Magazine, Issue 6, 3/2015
LIGO Scientific Collaboration Scientific LIGO issue 6 3/2015 LIGO MAGAZINE Fiat Lux: Hanford joins Livingston in Full Lock Detector Commissioning: Control Room Days and Nights An LHO engineer‘s perspective p. 6 The Transition of Gravitational Physics From Small to Big Science Part 1: The role of the NSF and the scientific community p. 14 ... and a take on undergrad research in LIGO! The cover image shows the LIGO Hanford X-arm end test mass (ETM). The image was captured by the Photon Calibrator Beam Localization Camera system. Behind the test mass hangs the reaction mass with its pattern of gold tracings that are part of the electrostatic drive control system. An arm cavity baffle partially occludes the view of the ETM surface. The Photon Calibrator, which was not operating when the photograph was taken, uses an auxiliary 1047 nm laser to induce calibrated sinusoidal displacements of the test mass via photon radiation pressure. The peak sinusoidally-modulated power in each laser beam is about 0.5 W. The beams reflect from the test mass surface at locations that are diametrically opposed and displaced vertically about the center of the mass. The positions of the beams must be maintained within a few milli- meters of the optimum locations to avoid calibration errors resulting from elastic deformation of the mass. A Matlab-based procedure developed by Darkhan Tuyenbayev (graduate student from UTB) and implemented by Thomas Abbott (graduate student from LSU) uses images of the ETM surface such as this, taken when the beams are present, to determine the posi- tions of the Photon Calibrator beams on the test mass surface. -

2003-Annual-Report.Pdf
Report by the Managing Director This volume presents a survey of the activities of the Albert Einstein Institute during 2003. This was a challenging year for the Institute, during which we had to cope with funding restrictions and intense competition from other institutions for some of our brightest young scientists. It was also a year in which we consolidated some important accomplishments: tangible progress toward the detection of gravitational waves; construction of our new laboratories in Hannover; the start of our research collaboration (a Sonderforschungsbereich) with the Universities of Jena, Tübingen, and Hannover and with the Max Planck Institute for Astrophysics; the start of the construction of the first space mission that the AEI has contributed to, LISA Pathfinder; preparations for our new International Max Planck Research School; the installation of a cluster supercomputer (called PEYOTE) to support our work on black hole simulations; and the expansion of our activities in electronic publishing. We hosted a number of workshops and meetings, and we had a very successful visit from our external scientific review committee (the Fachbeirat). Most important of all, our scientists were able to make significant progress in research in all our divisions. All the developments I mention here are described in more detail elsewhere in this report. In last year’s annual report we celebrated the opening of our experimental branch in Hannover. AEI/Hannover is a cooperation with the University of Hannover; it operates the GEO600 gravitational-wave detector and does research that will lead to new detectors, such as the high-profile NASA-ESA space mission called LISA. -

Britgravii-The Second British Gravity Meeting
BritGravII Second British Gravity Meeting School of Mathematical Sciences, Queen Mary, University of London Mon/Tue, June 10/11, 2002 The second of the annual BritGrav meetings on current research in Gravitational Physics in Britain took place at the School of Mathematical Sciences of Queen Mary, University of London on June 10/11, 2002. We tried to maintain the two good practices established at Southampton last year (see Carsten Gundlach’s report at gr-qc/0104062); namely allowing short talks of equal duration and keeping the participants’ expenses to a minimum. We were also able, with support from the groups below, to provide partial financial support for the younger participants. Altogether 95 participants took part, including a good number from research institutions outside Britain (namely, France, Sweden, Russia, Spain, Austria, USA, Portugal, Ireland, Germany, South Africa, Canada and Poland). There were a total of 47 talks — of 12 minutes duration each — over these two days. These included 1 talk by an undergraduate finalist, 15 talks by PhD students and 11 talks by postdoctoral researchers. The sessions were roughly grouped into the following categories: Classical General Relativity, Mathematical Studies, Quantum Gravitation, Quantum Theory on Curved Spacetimes, Alternative Models, Relativistic Astrophysics, Numerical Methods, and Other Topics. Below is the list of the abstracts of all the talks, in alphabetical order, submitted by the authors. The references to the electronic preprints at arXiv.org have been added where they exist. The BritGravII meeting was kindly supported financially by the London Mathematical Society, the Institute of Physics Mathematical and Theoretical Physics Group, the Institute of Physics Gravitational Physics Group, the scientific journal Classical and Quantum Gravity, and the School of Mathematical Sciences, Queen Mary, University of London.