Detecting Stable Clusters Using Principal Component Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Adaptive Wavelet Clustering for Highly Noisy Data
Adaptive Wavelet Clustering for Highly Noisy Data Zengjian Chen Jiayi Liu Yihe Deng Department of Computer Science Department of Computer Science Department of Mathematics Huazhong University of University of Massachusetts Amherst University of California, Los Angeles Science and Technology Massachusetts, USA California, USA Wuhan, China [email protected] [email protected] [email protected] Kun He* John E. Hopcroft Department of Computer Science Department of Computer Science Huazhong University of Science and Technology Cornell University Wuhan, China Ithaca, NY, USA [email protected] [email protected] Abstract—In this paper we make progress on the unsupervised Based on the pioneering work of Sheikholeslami that applies task of mining arbitrarily shaped clusters in highly noisy datasets, wavelet transform, originally used for signal processing, on which is a task present in many real-world applications. Based spatial data clustering [12], we propose a new wavelet based on the fundamental work that first applies a wavelet transform to data clustering, we propose an adaptive clustering algorithm, algorithm called AdaWave that can adaptively and effectively denoted as AdaWave, which exhibits favorable characteristics for uncover clusters in highly noisy data. To tackle general appli- clustering. By a self-adaptive thresholding technique, AdaWave cations, we assume that the clusters in a dataset do not follow is parameter free and can handle data in various situations. any specific distribution and can be arbitrarily shaped. It is deterministic, fast in linear time, order-insensitive, shape- To show the hardness of the clustering task, we first design insensitive, robust to highly noisy data, and requires no pre- knowledge on data models. -

Cluster Analysis, a Powerful Tool for Data Analysis in Education
International Statistical Institute, 56th Session, 2007: Rita Vasconcelos, Mßrcia Baptista Cluster Analysis, a powerful tool for data analysis in Education Vasconcelos, Rita Universidade da Madeira, Department of Mathematics and Engeneering Caminho da Penteada 9000-390 Funchal, Portugal E-mail: [email protected] Baptista, Márcia Direcção Regional de Saúde Pública Rua das Pretas 9000 Funchal, Portugal E-mail: [email protected] 1. Introduction A database was created after an inquiry to 14-15 - year old students, which was developed with the purpose of identifying the factors that could socially and pedagogically frame the results in Mathematics. The data was collected in eight schools in Funchal (Madeira Island), and we performed a Cluster Analysis as a first multivariate statistical approach to this database. We also developed a logistic regression analysis, as the study was carried out as a contribution to explain the success/failure in Mathematics. As a final step, the responses of both statistical analysis were studied. 2. Cluster Analysis approach The questions that arise when we try to frame socially and pedagogically the results in Mathematics of 14-15 - year old students, are concerned with the types of decisive factors in those results. It is somehow underlying our objectives to classify the students according to the factors understood by us as being decisive in students’ results. This is exactly the aim of Cluster Analysis. The hierarchical solution that can be observed in the dendogram presented in the next page, suggests that we should consider the 3 following clusters, since the distances increase substantially after it: Variables in Cluster1: mother qualifications; father qualifications; student’s results in Mathematics as classified by the school teacher; student’s results in the exam of Mathematics; time spent studying. -

Cluster Analysis Y H Chan
Basic Statistics For Doctors Singapore Med J 2005; 46(4) : 153 CME Article Biostatistics 304. Cluster analysis Y H Chan In Cluster analysis, we seek to identify the “natural” SPSS offers three separate approaches to structure of groups based on a multivariate profile, Cluster analysis, namely: TwoStep, K-Means and if it exists, which both minimises the within-group Hierarchical. We shall discuss the Hierarchical variation and maximises the between-group variation. approach first. This is chosen when we have little idea The objective is to perform data reduction into of the data structure. There are two basic hierarchical manageable bite-sizes which could be used in further clustering procedures – agglomerative or divisive. analysis or developing hypothesis concerning the Agglomerative starts with each object as a cluster nature of the data. It is exploratory, descriptive and and new clusters are combined until eventually all non-inferential. individuals are grouped into one large cluster. Divisive This technique will always create clusters, be it right proceeds in the opposite direction to agglomerative or wrong. The solutions are not unique since they methods. For n cases, there will be one-cluster to are dependent on the variables used and how cluster n-1 cluster solutions. membership is being defined. There are no essential In SPSS, go to Analyse, Classify, Hierarchical Cluster assumptions required for its use except that there must to get Template I be some regard to theoretical/conceptual rationale upon which the variables are selected. Template I. Hierarchical cluster analysis. For simplicity, we shall use 10 subjects to demonstrate how cluster analysis works. -

Cluster Analysis Objective: Group Data Points Into Classes of Similar Points Based on a Series of Variables
Multivariate Fundamentals: Distance Cluster Analysis Objective: Group data points into classes of similar points based on a series of variables Useful to find the true groups that are assumed to really exist, BUT if the analysis generates unexpected groupings it could inform new relationships you might want to investigate Also useful for data reduction by finding which data points are similar and allow for subsampling of the original dataset without losing information Alfred Louis Kroeber (1876-1961) The math behind cluster analysis A B C D … A 0 1.8 0.6 3.0 Once we calculate a distance matrix between points we B 1.8 0 2.5 3.3 use that information to build a tree C 0.6 2.5 0 2.2 D 3.0 3.3 2.2 0 … Ordination – visualizes the information in the distance calculations The result of a cluster analysis is a tree or dendrogram 0.6 1.8 4 2.5 3.0 2.2 3 3.3 2 distance 1 If distances are not equal between points we A C D can draw a “hanging tree” to illustrate distances 0 B Building trees & creating groups 1. Nearest Neighbour Method – create groups by starting with the smallest distances and build branches In effect we keep asking data matrix “Which plot is my nearest neighbour?” to add branches 2. Centroid Method – creates a group based on smallest distance to group centroid rather than group member First creates a group based on small distance then uses the centroid of that group to find which additional points belong in the same group 3. -

Cluster Analysis: What It Is and How to Use It Alyssa Wittle and Michael Stackhouse, Covance, Inc
PharmaSUG 2019 - Paper ST-183 Cluster Analysis: What It Is and How to Use It Alyssa Wittle and Michael Stackhouse, Covance, Inc. ABSTRACT A Cluster Analysis is a great way of looking across several related data points to find possible relationships within your data which you may not have expected. The basic approach of a cluster analysis is to do the following: transform the results of a series of related variables into a standardized value such as Z-scores, then combine these values and determine if there are trends across the data which may lend the data to divide into separate, distinct groups, or "clusters". A cluster is assigned at a subject level, to be used as a grouping variable or even as a response variable. Once these clusters have been determined and assigned, they can be used in your analysis model to observe if there is a significant difference between the results of these clusters within various parameters. For example, is a certain age group more likely to give more positive answers across all questionnaires in a study or integration? Cluster analysis can also be a good way of determining exploratory endpoints or focusing an analysis on a certain number of categories for a set of variables. This paper will instruct on approaches to a clustering analysis, how the results can be interpreted, and how clusters can be determined and analyzed using several programming methods and languages, including SAS, Python and R. Examples of clustering analyses and their interpretations will also be provided. INTRODUCTION A cluster analysis is a multivariate data exploration method gaining popularity in the industry. -

Factors Versus Clusters
Paper 2868-2018 Factors vs. Clusters Diana Suhr, SIR Consulting ABSTRACT Factor analysis is an exploratory statistical technique to investigate dimensions and the factor structure underlying a set of variables (items) while cluster analysis is an exploratory statistical technique to group observations (people, things, events) into clusters or groups so that the degree of association is strong between members of the same cluster and weak between members of different clusters. Factor and cluster analysis guidelines and SAS® code will be discussed as well as illustrating and discussing results for sample data analysis. Procedures shown will be PROC FACTOR, PROC CORR alpha, PROC STANDARDIZE, PROC CLUSTER, and PROC FASTCLUS. INTRODUCTION Exploratory factor analysis (EFA) investigates the possible underlying factor structure (dimensions) of a set of interrelated variables without imposing a preconceived structure on the outcome (Child, 1990). The analysis groups similar items to identify dimensions (also called factors or latent constructs). Exploratory cluster analysis (ECA) is a technique for dividing a multivariate dataset into “natural” clusters or groups. The technique involves identifying groups of individuals or objects that are similar to each other but different from individuals or objects in other groups. Cluster analysis, like factor analysis, makes no distinction between independent and dependent variables. Factor analysis reduces the number of variables by grouping them into a smaller set of factors. Cluster analysis reduces the number of observations by grouping them into a smaller set of clusters. There is no right or wrong answer to “how many factors or clusters should I keep?”. The answer depends on what you’re going to do with the factors or clusters. -

K-Means Clustering Via Principal Component Analysis
K-means Clustering via Principal Component Analysis Chris Ding [email protected] Xiaofeng He [email protected] Computational Research Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720 Abstract that data points belonging to same cluster are sim- Principal component analysis (PCA) is a ilar while data points belonging to different clusters widely used statistical technique for unsuper- are dissimilar. One of the most popular and efficient vised dimension reduction. K-means cluster- clustering methods is the K-means method (Hartigan ing is a commonly used data clustering for & Wang, 1979; Lloyd, 1957; MacQueen, 1967) which unsupervised learning tasks. Here we prove uses prototypes (centroids) to represent clusters by op- that principal components are the continuous timizing the squared error function. (A detail account solutions to the discrete cluster membership of K-means and related ISODATA methods are given indicators for K-means clustering. Equiva- in (Jain & Dubes, 1988), see also (Wallace, 1989).) lently, we show that the subspace spanned On the other end, high dimensional data are often by the cluster centroids are given by spec- transformed into lower dimensional data via the princi- tral expansion of the data covariance matrix pal component analysis (PCA)(Jolliffe, 2002) (or sin- truncated at K 1 terms. These results indi- gular value decomposition) where coherent patterns − cate that unsupervised dimension reduction can be detected more clearly. Such unsupervised di- is closely related to unsupervised learning. mension reduction is used in very broad areas such as On dimension reduction, the result provides meteorology, image processing, genomic analysis, and new insights to the observed effectiveness of information retrieval. -

Cluster Analysis
Cluster Analysis 1 2 3 4 5 Can we organize 6 sampling entities into Species discrete classes, such that Sites A B C D within-group similarity is 1 1 9 12 1 maximized and among- 2 1 8 11 1 3 1 6 10 10 group similarity is 4 10 0 9 10 minimized according to 5 10 2 8 10 some objective criterion? 6 10 0 7 2 1 Important Characteristics of Cluster Analysis Techniques P Family of techniques with similar goals. P Operate on data sets for which pre-specified, well-defined groups do "not" exist; characteristics of the data are used to assign entities into artificial groups. P Summarize data redundancy by reducing the information on the whole set of say N entities to information about say g groups of nearly similar entities (where hopefully g is very much smaller than N). 2 Important Characteristics of Cluster Analysis Techniques P Identify outliers by leaving them solitary or in small clusters, which may then be omitted from further analyses. P Eliminate noise from a multivariate data set by clustering nearly similar entities without requiring exact similarity. P Assess relationships within a single set of variables; no attempt is made to define the relationship between a set of independent variables and one or more dependent variables. 3 What’s a Cluster? A B E C D F 4 Cluster Analysis: The Data Set P Single set of variables; no distinction Variables between independent and dependent Sample x1 x2 x3 ... xp 1xx x ... x variables. 11 12 13 1p 2x21 x22 x23 .. -

A Nonparametric Statistical Approach to Clustering Via Mode Identification
Journal of Machine Learning Research 8 (2007) 1687-1723 Submitted 1/07; Revised 4/07; Published 8/07 A Nonparametric Statistical Approach to Clustering via Mode Identification Jia Li [email protected] Department of Statistics The Pennsylvania State University University Park, PA 16802, USA Surajit Ray [email protected] Department of Mathematics and Statistics Boston University Boston, MA 02215, USA Bruce G. Lindsay [email protected] Department of Statistics The Pennsylvania State University University Park, PA 16802, USA Editor: Charles Elkan Abstract A new clustering approach based on mode identification is developed by applying new optimiza- tion techniques to a nonparametric density estimator. A cluster is formed by those sample points that ascend to the same local maximum (mode) of the density function. The path from a point to its associated mode is efficiently solved by an EM-style algorithm, namely, the Modal EM (MEM). This method is then extended for hierarchical clustering by recursively locating modes of kernel density estimators with increasing bandwidths. Without model fitting, the mode-based clustering yields a density description for every cluster, a major advantage of mixture-model-based clustering. Moreover, it ensures that every cluster corresponds to a bump of the density. The issue of diagnos- ing clustering results is also investigated. Specifically, a pairwise separability measure for clusters is defined using the ridgeline between the density bumps of two clusters. The ridgeline is solved for by the Ridgeline EM (REM) algorithm, an extension of MEM. Based upon this new measure, a cluster merging procedure is created to enforce strong separation. -
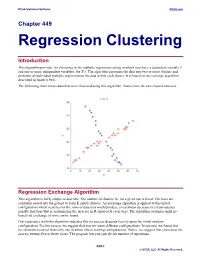
Regression Clustering
NCSS Statistical Software NCSS.com Chapter 449 Regression Clustering Introduction This algorithm provides for clustering in the multiple regression setting in which you have a dependent variable Y and one or more independent variables, the X’s. The algorithm partitions the data into two or more clusters and performs an individual multiple regression on the data within each cluster. It is based on an exchange algorithm described in Spath (1985). The following chart shows data that were clustered using this algorithm. Notice how the two clusters intersect. Regression Exchange Algorithm This algorithm is fairly simple to describe. The number of clusters, K, for a given run is fixed. The rows are randomly sorted into the groups to form K initial clusters. An exchange algorithm is applied to this initial configuration which searches for the rows of data that would produce a maximum decrease in a least-squares penalty function (that is, maximizing the increase in R-squared at each step). The algorithm continues until no beneficial exchange of rows can be found. Our experience with this algorithm indicates that its success depends heavily upon the initial-random configuration. For this reason, we suggest that you try many different configurations. In one test, we found that the optimum resulted from only one in about fifteen starting configurations. Hence, we suggest that you repeat the process twenty-five or thirty times. The program lets you specify the number of repetitions. 449-1 © NCSS, LLC. All Rights Reserved. NCSS Statistical Software NCSS.com Regression Clustering Number of Clusters A report is provided the gives the value of R-squared for each of the values of K. -

Statistical Power for Cluster Analysis
Statistical power for cluster analysis Edwin S. Dalmaijer, Camilla L. Nord, & Duncan E. Astle MRC Cognition and Brain Sciences Unit, University of Cambridge, Cambridge, United Kingdom Corresponding author Dr Edwin S. Dalmaijer, MRC Cognition and Brain Sciences Unit, 15 Chaucer Road, Cambridge, CB2 7EF, United Kingdom. Telephone: 0044 1223 769 447. Email: edwin.dalmaijer@mrc- cbu.cam.ac.uk 1 Abstract Background. Cluster algorithms are gaining in popularity in biomedical research due to their compelling ability to identify discrete subgroups in data, and their increasing accessibility in mainstream software. While guidelines exist for algorithm selection and outcome evaluation, there are no firmly established ways of computing a priori statistical power for cluster analysis. Here, we estimated power and classification accuracy for common analysis pipelines through simulation. We systematically varied subgroup size, number, separation (effect size), and covariance structure. We then subjected generated datasets to dimensionality reduction approaches (none, multi-dimensional scaling, or uniform manifold approximation and projection) and cluster algorithms (k-means, agglomerative hierarchical clustering with Ward or average linkage and Euclidean or cosine distance, HDBSCAN). Finally, we directly compared the statistical power of discrete (k-means), “fuzzy” (c-means), and finite mixture modelling approaches (which include latent class analysis and latent profile analysis). Results. We found that clustering outcomes were driven by large effect sizes or the accumulation of many smaller effects across features, and were mostly unaffected by differences in covariance structure. Sufficient statistical power was achieved with relatively small samples (N=20 per subgroup), provided cluster separation is large (Δ=4). Finally, we demonstrated that fuzzy clustering can provide a more parsimonious and powerful alternative for identifying separable multivariate normal distributions, particularly those with slightly lower centroid separation (Δ=3). -

Simultaneous Clustering and Estimation of Heterogeneous Graphical Models
Journal of Machine Learning Research 18 (2018) 1-58 Submitted 1/17; Revised 11/17; Published 4/18 Simultaneous Clustering and Estimation of Heterogeneous Graphical Models Botao Hao [email protected] Department of Statistics Purdue University West Lafayette, IN 47906, USA Will Wei Sun [email protected] Department of Management Science University of Miami School of Business Administration Miami, FL 33146, USA Yufeng Liu [email protected] Department of Statistics and Operations Research Department of Genetics Department of Biostatistics Carolina Center for Genome Sciences Lineberger Comprehensive Cancer Center University of North Carolina at Chapel Hill Chapel Hill, NC 27599, USA Guang Cheng [email protected] Department of Statistics Purdue University West Lafayette, IN 47906, USA Editor: Koji Tsuda Abstract We consider joint estimation of multiple graphical models arising from heterogeneous and high-dimensional observations. Unlike most previous approaches which assume that the cluster structure is given in advance, an appealing feature of our method is to learn cluster structure while estimating heterogeneous graphical models. This is achieved via a high di- mensional version of Expectation Conditional Maximization (ECM) algorithm (Meng and Rubin, 1993). A joint graphical lasso penalty is imposed on the conditional maximiza- tion step to extract both homogeneity and heterogeneity components across all clusters. Our algorithm is computationally efficient due to fast sparse learning routines and can be implemented without unsupervised learning knowledge. The superior performance of our method is demonstrated by extensive experiments and its application to a Glioblastoma cancer dataset reveals some new insights in understanding the Glioblastoma cancer. In theory, a non-asymptotic error bound is established for the output directly from our high dimensional ECM algorithm, and it consists of two quantities: statistical error (statisti- cal accuracy) and optimization error (computational complexity).