An Analysis and Design Tool for HCI
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

EPL-0010589 Article-2
This is an electronic reprint of the original article. This reprint may differ from the original in pagination and typographic detail. Korhonen, O.; Forsman, N.; Österberg, M.; Budtova, T. Eco-friendly surface hydrophobization of all-cellulose composites using layer-by-layer deposition Published in: Express Polymer Letters DOI: 10.3144/expresspolymlett.2020.74 Published: 01/10/2020 Document Version Publisher's PDF, also known as Version of record Please cite the original version: Korhonen, O., Forsman, N., Österberg, M., & Budtova, T. (2020). Eco-friendly surface hydrophobization of all- cellulose composites using layer-by-layer deposition. Express Polymer Letters, 14(10), 896-907. https://doi.org/10.3144/expresspolymlett.2020.74 This material is protected by copyright and other intellectual property rights, and duplication or sale of all or part of any of the repository collections is not permitted, except that material may be duplicated by you for your research use or educational purposes in electronic or print form. You must obtain permission for any other use. Electronic or print copies may not be offered, whether for sale or otherwise to anyone who is not an authorised user. Powered by TCPDF (www.tcpdf.org) eXPRESS Polymer Letters Vol.14, No.10 (2020) 896–907 Available online at www.expresspolymlett.com https://doi.org/10.3144/expresspolymlett.2020.74 Eco-friendly surface hydrophobization of all-cellulose composites using layer-by-layer deposition O. Korhonen1, N. Forsman1, M. Österberg1, T. Budtova1,2* 1Aalto University, School of Chemical Engineering, Department of Bioproducts and Biosystems, P.O. Box 16300, 00076 Aalto, Finland 2MINES ParisTech, PSL Research University, CEMEF – Center for materials forming, UMR CNRS 7635, CS 10207, 06904 Sophia Antipolis, France Received 14 January 2020; accepted in revised form 3 March 2020 Abstract. -

ITG Meeting 26
www.sail-project.eu Capacity Sharing Workshop Agenda 8:30 Registration & Coffee 8:45 Welcome 9:00 Session 1: Network Emulation & Simulation Scalability Engineering innovations applicable to mobile/cellular (ConEx), Bob Briscoe (BT) Congestion Exposure in Mobility Scenarios, Faisal Ghias Mir, Dirk Kutscher, Marcus Brunner (NEC) Enhanced Capacity Management – how to monitor, control, and steer your service quality, Dr. Wolfgang Knospe (Detecon) Bridging QoE and QoS for Mobile Broadband Networks, David Soldani (Huawei) 10:45 Coffee break 11:00 Session 2: Transport Layer QoS Considerations for controlling TCP's fairness on end hosts, Michael Welzl (Department of Informatics, University of Oslo) Trading loss against delay in Networked Control Systems, Rainer Blind (Networked Control Systems (NCS), University of Stuttgart) Fair Background Data Transfers of Minimal Delay Impact, Costas Courcoubetis, Antonis Dimakis (Athens University of Economics and Business) Multipath Transport Challenges and Solutions, Michael Scharf (Bell Labs Stuttgart) 12:45 Lunch 13:45 Session 3: QoS in Wireless Networks QoS and QoE in the Next Generation Networks: application to wireless networks, Prof. Pascal Lorenz (University of Haute Alsace) Improving the Usability of Cellular Charging Solutions, Christian Hoene (University of Tübingen) Context-Aware Resource Allocation for Media Streaming: Exploiting Mobility and Application-Layer Predictions, Hatem Abou-zeid, Stefan Valentin (Bell Labs Stuttgart) and Hossam Hassanein (Queen's University, Canada) Context-aware Scheduling -

Wojciech Tomasz Sołowski Date of Birth
Name: Wojciech Tomasz Sołowski Date of Birth: 25th December 1978 Mobile: +358 (0) 505925254 Email (work): [email protected] Email (private) : [email protected] Webpage (work) : https://people.aalto.fi/wojciech.solowski Webpage (private) : https://solowski.info Address (work): Civil Engineering Department, Aalto University, Rakentajanaukio 4, Espoo, Finland Education: PhD (Durham), MEng (Silesian University of Technology) Languages: English (fluent), German (Zentrale Mittelstufe Prűfung, ZMP), French (B2/B1 level), Finnish (B1/B2), basic Russian Research interests: Material point method (development, validation, use in geomechanics), constitutive modelling of soils, unsaturated soils – in particular in application for nuclear waste disposal sites, links between soil microstructure and its macroscopic behaviour, stress integration algorithms, computational algorithms, cyclic loading, soil improvement methods, soil dynamics Other Interests: computers, technology, programming, artificial intelligence, economics, badminton, tennis, bridge, tai-chi. Web : https://people.aalto.fi/en/wojciech_solowski https://solowski.info Affiliations 2017 – current Assistant Professor (2), Aalto University, Finland 2014 – 2017 Assistant Professor (1), Aalto University, Finland 2009 – 2014 Research Associate, University of Newcastle, Australia 2005 – 2008 Marie – Curie Early Stage Research Fellow, Durham University, UK. Research area: constitutive modelling of unsaturated soils, implementation of unsaturated soil models into Finite Element -

Aalto University Is a Community of Bold Thinkers Where Science and Art Meet Technology and Business
Assistant professor in Marketing (tenure track) Application closes on: 17.5.2021 Place: Department of Marketing Position: Tenure track Aalto University is a community of bold thinkers where science and art meet technology and business. We are committed to identifying and solving grand societal challenges and building an innovative future. Aalto has six schools with nearly 11 000 students and a staff of more than 4000, of which 400 are professors. Our main campus is located in Espoo, Finland. Diversity is part of who we are, and we actively work to ensure our community’s diversity and inclusiveness in the future as well. This is why we warmly encourage qualified candidates from all backgrounds to join our community. The Department of Marketing at Aalto University School of Business invites applications for full-time fixed-term position as Assistant professor in Marketing Your role and goals The candidate is expected to exercise and guide scientific research, to provide related higher academic education, to follow the advances of their field, to participate in service to the Aalto University community and to take part in societal interaction and international collaboration in their field. The position will be filled on the Assistant professor level (1st term 2021). The department welcomes applicants with strong methodological knowhow and background in some combination of data analytics, quantitative research methods, modelling, simulations, AI and data science broadly speaking, and expertise in applying these skills in marketing. The department also encourages excellent marketing scholars from outside these methodological fields to apply. Consistent with departmental culture and Aalto School of Business’ mission we welcome creativity as well as substantive and methodological expertise. -

Hemeida, Ahmed
This is an electronic reprint of the original article. This reprint may differ from the original in pagination and typographic detail. Hemeida, Ahmed; Lehikoinen, Antti; Rasilo, Paavo; Vansompel, Hendrik; Belahcen, Anouar; Arkkio, Antero; Sergeant, Peter A Simple and Efficient Quasi-3D Magnetic Equivalent Circuit for Surface Axial Flux Permanent Magnet Synchronous Machines Published in: IEEE Transactions on Industrial Electronics DOI: 10.1109/TIE.2018.2884212 Published: 01/11/2019 Document Version Peer reviewed version Please cite the original version: Hemeida, A., Lehikoinen, A., Rasilo, P., Vansompel, H., Belahcen, A., Arkkio, A., & Sergeant, P. (2019). A Simple and Efficient Quasi-3D Magnetic Equivalent Circuit for Surface Axial Flux Permanent Magnet Synchronous Machines. IEEE Transactions on Industrial Electronics, 66(11), 8318-8333. https://doi.org/10.1109/TIE.2018.2884212 This material is protected by copyright and other intellectual property rights, and duplication or sale of all or part of any of the repository collections is not permitted, except that material may be duplicated by you for your research use or educational purposes in electronic or print form. You must obtain permission for any other use. Electronic or print copies may not be offered, whether for sale or otherwise to anyone who is not an authorised user. Powered by TCPDF (www.tcpdf.org) © 2018 IEEE. This is the author’s version of an article that has been published by IEEE. Personal use of this material is permitted. Permission from IEEE must be obtained for all other uses, in any current or future media, including reprinting/republishing this material for advertising or promotional purposes, creating new collective works, for resale or redistribution to servers or lists, or reuse of any copyrighted component of this work in other works. -

Aalto University Website Website for Incoming Exchange Students Website for International Students at Aalto
Important links: Aalto University website Website for incoming exchange students Website for international students at Aalto Aalto University Schools of Technology Information sheet 2021-2022 Study fields Please click the School name for course lists. School of Chemical Engineering • Biomass Refining • Fibre and Polymer Engineering • Biotechnology • Chemistry • Functional Materials • Sustainable Metals Processing • Chemical and Process Engineering • Biosystems and Biomaterials School of Electrical Engineering • Automation and Systems Technology • Communications Engineering • Electronics and Electrical Engineering • Bioinformation Technology School of Engineering • Building Technology • Energy Technology • Geoengineering • Geoinformatics • Mechanical Engineering • Real Estate Economics • Spatial Planning and Transportation Engineering • Water and Environmental Engineering School of Science • Computer Science • Industrial Engineering and Management • Engineering Physics • Mathematics and Operations Research • Biomedical Engineering and Neuroscience Academic matters Courses for At least 2/3 of the courses should be selected from one school. The remaining 1/3 can exchange students be taken from other Schools of Technology in Aalto University, as long as the prereq- uisites are met. Exchange students are not allowed to take courses from the School of Arts, Design and Architecture or the School of Business, except for cross-school courses, univer- sity wide studies and interdisciplinary studies. For more information on studies, please see Into website. There are some changes in the course selection every year, the study programmes are updated during the summer. Students must be prepared to make changes in their study plans upon arrival. Regardless of study level, exchange students can choose both Bachelor and Master level courses, provided that the prerequisites are met. The majority of courses of- fered in English are on the Master level. -

Curriculum Vitae Pia Christina Fricker
curriculum vitae Pia Christina Fricker Full name and date Name Pia Christina Fricker Gender Female Date of writing CV 23.04.2018 Date and place of birth, nationality, current residence Date of Birth 17.06.1974 Place of Birth Karlsruhe, Germany Nationality Finnish Family Status married Current Residence Kontiontie 3 E 38 FIN 02110 Espoo [email protected] + 358 503087105 Education and degrees awarded Doctoral Studies PhD student, ETH Zurich (CH): to be finished end of 2018 Postgraduate Studies Diploma Master of Advanced Studies in Computer Aided Architectural Design (MAS.CAAD.ETHZ): 2002 - 2003, (65 ects) – parametric design in architecture, Prof. Ludger Hovestadt, Chair for Computer Aided Architectural Design, Dept. for Architecture, ETH Zurich (CH), final grade: excellent Academic Studies M.Sc. Architecture (Dipl.Ing): 2001, Technical University Karlsruhe (DE), topic: Hafencity Hamburg, supervisor Prof. Dr. Günther Uhlig, Prof. Henri Bava, specification in landscape architecture and urban design, final grade: excellent Other education and training, qualifications and skills Further Education Construction Manager: 2004, Baugewerbliche Berufsschule Zurich, (CH) International mobility 1998-1999, Department of Architecture, HUT: Technical University Helsinki, and Department of Architecture, TUT: Technical University of Tampere, (FIN) Linguistic skills Language Skills German: native speaker English: fluent, spoken and written (CEF level C2) Finnish: good command, spoken and written (CEF level B2) French: good command, spoken and written (CEF level B2) Swedish: basic communication skills (CEF level A2) Current position Current position since August 2017: Professor, Professorship for Computational Methodologies in Landscape Architecture and Urbanism, Dept. for Architecture Employeer Aalto University, School of Art, Design and Architecture 1 | CV . -

Curriculum Vitae
Debopam Bhattacherjee PhD Candidate, Final (5th) year Email: [email protected] Network Design Lab (ND), Systems Group, Phone: +41 779421314 Department of Computer Science, ETH Zürich Web: https://bdebopam.github.io EDUCATION M.S. Security and Mobile Computing (NordSecMob) KTH Royal Institute of Technology, Sweden + Aalto University, Finland, 2016 B.E. Computer Science & Engineering Jadavpur University, India, 2009 EMPLOYMENT 10/2016 – Systems Group, Department of Computer Science, ETH Zürich, Switzerland PhD Candidate, Network Design Lab PhD supervisor: Prof. Dr. Ankit Singla 06/2019 – 08/2019 Max Planck Institute for Informatics, Saarbrücken, Germany Research Fellow at Internet Architecture group Supervisor: Prof. Dr. Anja Feldmann 06/2015 – 07/2016 Computer Science and Engineering Dept., Aalto University, Finland Research/Teaching Assistant Supervisor: Prof. Dr. Tuomas Aura, Prof. Dr. Andrei Gurtov 08/2009 – 08/2014 PwC & Deloitte, India Senior Technology Consultant, Technology Consultant RESEARCH INTERESTS Low-Earth orbit satellite networks, Internet architecture, low-latency networks and applications, congestion control. PUBLICATIONS Refereed Publications 2020 In-orbit computing: an outlandish thought experiment? [ACM HotNets] (DB, Simon Kassing), Melissa Licciardello, Ankit Singla 2020 “Internet from Space” without Inter-satellite Links? [ACM HotNets] Yannick Hauri, DB, Manuel Grossmann, Ankit Singla 2020 Exploring the “Internet from space” with Hypatia [ACM IMC] (Simon Kassing, DB), André Baptista Águas, Jens Eirik -

Yarom, Yuval "Make Sure DSA Signing Exponentiations Really Are Constant-Time"
This is an electronic reprint of the original article. This reprint may differ from the original in pagination and typographic detail. García, Cesar Pereida; Brumley, Billy Bob; Yarom, Yuval "Make sure DSA signing exponentiations really are constant-time" Published in: CCS 2016 - Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security DOI: 10.1145/2976749.2978420 Published: 24/10/2016 Document Version Publisher's PDF, also known as Version of record Published under the following license: CC BY-NC-SA Please cite the original version: García, C. P., Brumley, B. B., & Yarom, Y. (2016). "Make sure DSA signing exponentiations really are constant- time". In CCS 2016 - Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security (Vol. 24-28-October-2016, pp. 1639-1650). ACM. https://doi.org/10.1145/2976749.2978420 This material is protected by copyright and other intellectual property rights, and duplication or sale of all or part of any of the repository collections is not permitted, except that material may be duplicated by you for your research use or educational purposes in electronic or print form. You must obtain permission for any other use. Electronic or print copies may not be offered, whether for sale or otherwise to anyone who is not an authorised user. Powered by TCPDF (www.tcpdf.org) “Make Sure DSA Signing Exponentiations Really are Constant-Time” Cesar Pereida García Billy Bob Brumley Yuval Yarom Department of Computer Department of Pervasive The University of Adelaide and Science Computing Data61, CSIRO, Australia Aalto University, Finland Tampere University of [email protected] cesar.pereida@aalto.fi Technology, Finland billy.brumley@tut.fi ABSTRACT Our attack builds upon several techniques to profile the TLS and SSH are two of the most commonly used proto- cache memory and capture timing signals. -

1-S2.0-S0040162518316378-Main
This is an electronic reprint of the original article. This reprint may differ from the original in pagination and typographic detail. Vicente-Saez, Ruben; Gustafsson, Robin; Van den Brande, Lieve The dawn of an open exploration era Published in: Technological Forecasting and Social Change DOI: 10.1016/j.techfore.2020.120037 Published: 01/07/2020 Document Version Publisher's PDF, also known as Version of record Published under the following license: CC BY Please cite the original version: Vicente-Saez, R., Gustafsson, R., & Van den Brande, L. (2020). The dawn of an open exploration era: Emergent principles and practices of open science and innovation of university research teams in a digital world. Technological Forecasting and Social Change, 156, [120037]. https://doi.org/10.1016/j.techfore.2020.120037 This material is protected by copyright and other intellectual property rights, and duplication or sale of all or part of any of the repository collections is not permitted, except that material may be duplicated by you for your research use or educational purposes in electronic or print form. You must obtain permission for any other use. Electronic or print copies may not be offered, whether for sale or otherwise to anyone who is not an authorised user. Powered by TCPDF (www.tcpdf.org) Technological Forecasting & Social Change 156 (2020) 120037 Contents lists available at ScienceDirect Technological Forecasting & Social Change journal homepage: www.elsevier.com/locate/techfore The dawn of an open exploration era: Emergent principles and practices of T open science and innovation of university research teams in a digital world ⁎ Ruben Vicente-Saeza,b, , Robin Gustafssona, Lieve Van den Brandec,d a Aalto University, Finland b University of Valencia, Spain c European Commission - DG Employment, Belgium d Free University of Brussels (VUB), Belgium ARTICLE INFO ABSTRACT Keywords: Principles and practices of open science at universities are evolving. -
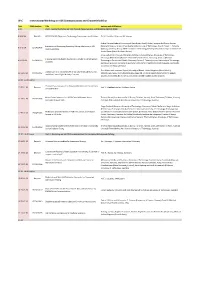
W-C International Workshop on V2X Communications and Channel Modeling
W-C International Workshop on V2X Communications and Channel Modeling Time EDAS Number Title Authors with Affiliations 9.00 Part I - Second Workshop on V2X Channel Measurements and Modeling (WVCM 2018) 9.00-9.36 Keynote H2020 5GCAR: Objectives, Technology Components and Enablers Dr. M. Condoluci, Ericsson AB, Sweden Gabriel Guieiro (Federal University of Ouro Preto, Brazil); Pedro Henrique de Oliveira Gomes Evaluation of Shadowing Caused by Mining Machinery in V2I (Federal University of Ouro Preto & Vale Institute of Technology, Brazil); Erika P. L. Almeida 9.37-9.54 1570460403 Communications (Aalborg University & INDT - Institute of Technology Development, Denmark); Luis Guilherme Uzeda Garcia (Nokia Bell Labs, France) Jonas Gedschold, Christian Schneider and Martin Käske (Ilmenau University of Technology, Germany); Mate Boban (Huawei German Research Center, Germany); Jian Luo (Huawei Tracking Based Multipath Clustering in Vehicle-to-Infrastructure 9.55-10.13 1570459752 Technologies Duesseldorf GmbH, Germany); Reiner S. Thomä (Ilmenau University of Technology, Channels Germany); Giovanni Del Galdo (Fraunhofer Institute for Integrated Circuits IIS & Technische Universität Ilmenau, Germany) Fred Wiffen and Lawrence Sayer (University of Bristol, United Kingdom (Great Britain)); Comparison of OTFS and OFDM in Ray Launched sub-6GHz and 10.13-10.30 1570463462 Mohammud Z Bocus (Toshiba Research Europe Ltd, United Kingdom (Great Britain)); Angela mmWave Line-of-Sight Mobility Channels Doufexi and Andrew Nix (University of Bristol, -

METAMORPHOSE VI – the Virtual Institute
METAMORPHOSE VI – the Virtual Institute for artificial electromagnetic materials and metamaterials: Origin, mission, and activities Bilotti, F., Rockstuhl, C., Schuchinsky, A., & Tretyakov, S. (2014). METAMORPHOSE VI – the Virtual Institute for artificial electromagnetic materials and metamaterials: Origin, mission, and activities. EPJ Advanced Metamaterials, 1(1). https://doi.org/10.1051/epjam/2014002 Published in: EPJ Advanced Metamaterials Document Version: Publisher's PDF, also known as Version of record Queen's University Belfast - Research Portal: Link to publication record in Queen's University Belfast Research Portal Publisher rights © F. Bilotti et al., Published by EDP Sciences, 2014 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. General rights Copyright for the publications made accessible via the Queen's University Belfast Research Portal is retained by the author(s) and / or other copyright owners and it is a condition of accessing these publications that users recognise and abide by the legal requirements associated with these rights. Take down policy The Research Portal is Queen's institutional repository that provides access to Queen's research output. Every effort has been made to ensure that content in the Research Portal does not infringe any person's rights, or applicable UK laws. If you discover content in the Research Portal that you believe breaches copyright or violates any law, please contact [email protected]. Download date:24. Sep. 2021 EPJ Appl. Metamat. 2014, 1,1 Ó F.