Towards Verifiable Adaptive Control of Gas Turbine Engines
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Turbine Bonanza
While others fiddle, Allison blazes ahead with a private turboprop. BY MARK M. LACAGNINA Timing is a critical element in the suc• for these applications have been either prop that were replaced. This is not cess or failure of any new concept or abandoned or put on the back burner directly translatable to increased pay• design. Powered flight, a concept pro• due to lack of adequate financing or load, however, because each gallon of posed centuries ago by visionaries such because those involved in the projects jet fuel in the Turbine Bonanza's fuel as Roger Bacon and Leonardo da Vinci, do not believe the time (that is, the tanks weighs about 0.7 pounds more remained little more than whimsy until market) is right. than the avgas previously required for society and technology were ready for There is at least one exception. The the piston engine. The lighter engine it. The first mechanism generally cred• Allison Gas Turbine Division of Gen• was installed in such a way as to re• ited with achieving powered flight eral Motors, which is working with quire no changes to the Bonanza's used wing-warping for flight control. It Soloy on the Allison-powered Turbine certificated center-of-gravity limits. As worked well enough 80 years ago but 206 and other applications, believes a result, the propeller arc is 22 inches would be only of passing interest to the time is, indeed, right for a farther forward. modern aerodynamic engineers. Con• nonutility turbine single. The company When I visited Allison's Indianapolis versely, such things as stall fences and currently is test-flying a Turbine Bo• headquarters in July, the Turbine Bo• boosted controls, designs that have nanza with the intent of obtaining a nanza had been flown only about 100 applications today, would have been of supplemental type certificate (STC) for hours. -

October 2003 Alerts
October 2003 FAA AC 43-16A CONTENTS AIRPLANES BEECH ........................................................................................................................................ 1 CESSNA ..................................................................................................................................... 2 PIPER .......................................................................................................................................... 3 POWERPLANTS AND PROPELLERS TELEDYNE CONTINENTAL MOTOR .................................................................................... 4 AIR NOTES ELECTRONIC VERSION OF MALFUNCTION OR DEFECT REPORT ................................ 4 SERVICE DIFFICULTY REPORTING PROGRAM.................................................................. 5 IF YOU WANT TO CONTACT US .......................................................................................... 6 AVIATION SERVICE DIFFICULTY REPORTS....................................................................... 6 1 October 2003U.S. DEPARTMENT OF TRANSPORTATION FAA AC 43-16A FEDERAL AVIATION ADMINISTRATION WASHINGTON, DC 20590 AVIATION MAINTENANCE ALERTS The Aviation Maintenance Alerts provide a common communication channel through which the aviation community can economically interchange service experience and thereby cooperate in the improvement of aeronautical product durability, reliability, and safety. This publication is prepared from information submitted by those who operate and maintain civil aeronautical -

Word to PDF Converter - Unregistered
( Word to PDF Converter - Unregistered ) http://www.Word-to-PDF-Converter.net LANDING GEAR LANDING GEAR SYSTEMS Learning Objective: Identify the various types of landing gear systems used on fixed-wing and rotary-wing aircraft. Every aircraft maintained in today is equipped with a landing gear system. Most aircraft also use arresting and catapult gear. The landing gear is that portion of the aircraft that supports the weight of the aircraft while it is on the ground. The landing gear contains components that are necessary for taking off and landing the aircraft safely. Some of these com-ponents are landing gear struts that absorb landing and taxiing shocks; brakes that are used to stop and, in some cases, steer the aircraft; nosewheel steering for steering the aircraft; and in some cases, nose catapult com-ponents that provide the aircraft with carrier deck takeoff capabilities. FIXED-WING AIRCRAFT Landing gear systems in fixed-wing aircraft are similar in design. Most aircraft are equipped with the tricycle-type retractable landing gear. Some types of landing gear are actuated in different sequences and directions, but practically all are hydraulically operated and electrically controlled. With a knowledge of basic hydraulics and familiarity with the operation of actuating system components, you should be able to understand the operational and troubleshooting procedures for landing gear systems. Main Landing Gear The typical aircraft landing gear assembly consists of two main landing gears and one steerable nose landing gear. As you can see in figure Figure 12-1.–Tricycle landing gear. is installed under each wing. Because aircraft are different in size, shape, and construction, every landing gear is specially designed. -
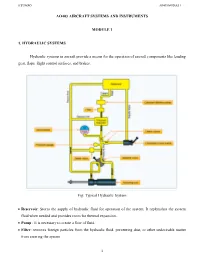
Ao403 Module 1
JCET/AERO AO403 MODULE 1 AO403 AIRCRAFT SYSTEMS AND INSTRUMENTS MODULE 1 1. HYDRAULIC SYSTEMS Hydraulic systems in aircraft provide a means for the operation of aircraft components like landing gear, flaps, flight control surfaces, and brakes. Fig: Typical Hydraulic System Reservoir: Stores the supply of hydraulic fluid for operation of the system. It replenishes the system fluid when needed and provides room for thermal expansion. Pump : It is necessary to create a flow of fluid. Filter: removes foreign particles from the hydraulic fluid, preventing dust, or other undesirable matter from entering the system. 1 JCET/AERO AO403 MODULE 1 Pressure Regulator: Unloads or relieves the power-driven pump when the desired pressure in the system is reached. Thus, it is often referred to as an unloading valve. Accumulator: It serves a twofold purpose: . It acts as a shock absorber by maintaining an even pressure in the system. It stores enough fluid under pressure to provide for emergency operation of certain actuating units. Check valves: Allow the flow of fluid in one direction only. Pressure gage: Indicates the amount of hydraulic pressure in the system. Relief valve: Safety valve installed in the system to bypass fluid through the valve back to the reservoir in case excessive pressure is built up in the system. Selector valve: Used to direct the flow of fluid. These valves are normally actuated by solenoids or manually operated, either directly or indirectly through use of mechanical linkage. Actuating cylinder: Converts fluid pressure into useful work by linear or reciprocating mechanical motion. 1.1 Advantages of Hydraulic system • Large load capacity with almost high accuracy and precision. -

Aircraft Systems.Pdf
AERONAUTICAL ENGINEERING MRCET (UGC Autonomous) AIRCRAFT SYSTEMS COURSE FILE IV yr B.Tech I Sem (2019-2020) Prepared By Mr. Sachin Srivastava, Assist. Prof Department of Aeronautical Engineering MALLA REDDY COLLEGE OF ENGINEERING & TECHNOLOGY (Autonomous Institution UGC, Govt. of India) Affiliated to JNTU, Hyderabad, Approved by AICTE Accredited by NBA & NAAC, A Grade – ISO9001:2015Certified) Maisammaguda, Dhulapally (Post Via. Kompally), Secunderabad 500100, Telangana State, India. IV I B. Tech Aircraft Systems by Sachin Srivastava I AERONAUTICAL ENGINEERING MRCET (UGC Autonomous) MRCET VISION To become a model institution in the fields of Engineering, Technology and Management. To have a perfect synchronization of the ideologies of MRCET with challenging demands of International Pioneering Organizations. MRCET MISSION To establish a pedestal for the integral innovation, team spirit, originality and competence in the students, expose them to face the global challenges and become pioneers of Indian vision of modern society. MRCET QUALITY POLICY To pursue continual improvement of teaching learning process of Undergraduate and Post Graduate programs in Engineering & Management vigorously. To provide state of art infrastructure and expertise to impart the quality education. IV I B. Tech Aircraft Systems by Sachin Srivastava II AERONAUTICAL ENGINEERING MRCET (UGC Autonomous) PROGRAM OUTCOMES (PO s) Engineering Graduates will be able to: 1. Engineering knowledge: Apply the knowledge of mathematics, science, engineering fundamentals, and an -

Propulsion Control Technology Development in the United States a Historical Perspective
NASA/TM—2005-213978 Propulsion Control Technology Development in the United States A Historical Perspective Link C. Jaw Scientific Monitoring, Inc., Scottsdale, Arizona Sanjay Garg Glenn Research Center, Cleveland, Ohio October 2005 The NASA STI Program Office . in Profile Since its founding, NASA has been dedicated to • CONFERENCE PUBLICATION. Collected the advancement of aeronautics and space papers from scientific and technical science. The NASA Scientific and Technical conferences, symposia, seminars, or other Information (STI) Program Office plays a key part meetings sponsored or cosponsored by in helping NASA maintain this important role. NASA. The NASA STI Program Office is operated by • SPECIAL PUBLICATION. Scientific, Langley Research Center, the Lead Center for technical, or historical information from NASA’s scientific and technical information. The NASA programs, projects, and missions, NASA STI Program Office provides access to the often concerned with subjects having NASA STI Database, the largest collection of substantial public interest. aeronautical and space science STI in the world. The Program Office is also NASA’s institutional • TECHNICAL TRANSLATION. English- mechanism for disseminating the results of its language translations of foreign scientific research and development activities. These results and technical material pertinent to NASA’s are published by NASA in the NASA STI Report mission. Series, which includes the following report types: Specialized services that complement the STI • TECHNICAL PUBLICATION. Reports of Program Office’s diverse offerings include completed research or a major significant creating custom thesauri, building customized phase of research that present the results of databases, organizing and publishing research NASA programs and include extensive data results . even providing videos. -

Mcfarlane Aviation Products FAA-Pmamcfarlane Manufacturer Aviation of Quality Aircraft Products Parts 2017 Catalog
McFarlane Aviation Products FAA-PMAMcFarlane Manufacturer Aviation of Quality Aircraft Products Parts 2017 Catalog Sample pages only! Contact us for your own FULL 236 page catalogue! New Products! New!McFar Cowllane Avia tionFlap Products Hinges for Cessna Aircraft New! Fuel Gascolator Assemblies New! Control Yoke Replace worn-out cowl flap hinges at half the cost! Fast and Easy to Maintain! Universal Joint Kits Assembly includes hinge and hinge pin FAA-PMA Approved for many light aircraft for Piper Aircraft Now Stainless Steel for longer wear! Page 44 Page 49-50 Page 101 New! Flight Control Cable New! Bulk New! Flight Control Cable New! Stabilizer Jack Screw Kits for Caravan Aircraft Thermocoupler Kits for Beechcraft Aircraft Pin Tool for Cessna McFarlane has complete stock Wire from Complete kits for 35 and 36 180, 182 and 185 Aircraft of FAA-PMA cables for the Tempest/Alcor series Beechcraft Aircraft Avoid Costly Damage! Caravan Aircraft For Cessna 180, 182, 185 jack screws pin Pages 84-85 Page 69 Pages 95-98 New! Trim Wheel Stop Catch Assembly New! Pulley Kits for Caravan for Cessna Aircraft Aircraft Save more than 75%! Longer Service Life! Page 103 Pages 104-105 Page 231 New! Trim Wheel Shafts and New! Aileron, Elevator, Flap and New! Brake Assembly and Sprockets for Cessna Aircraft Rudder Skins for Cessna Aircraft Master Cylinder Seal Kits for Improved Design! Skins for early models - Expanded Eligibility! Cessna Aircraft Better and costs less! Save time and $$ with kits containing just the parts you need! Page 102 Page 106-107 -
Stability and Performance of Propulsion Control Systems with Distributed Control Architectures and Failures
STABILITY AND PERFORMANCE OF PROPULSION CONTROL SYSTEMS WITH DISTRIBUTED CONTROL ARCHITECTURES AND FAILURES DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Rohit K. Belapurkar, M.S. Graduate Program in Aeronautical and Astronautical Engineering The Ohio State University 2012 Dissertation Committee: Prof. Rama K. Yedavalli, Advisor Prof. Meyer Benzakein Prof. Krishnaswamy Srinivasan Copyright by Rohit K. Belapurkar 2012 ABSTRACT Future aircraft engine control systems will be based on a distributed architecture, in which, the sensors and actuators will be connected to the controller through an engine area network. Distributed engine control architecture enables the use of advanced control techniques along with achieving weight reduction, improvement in performance and lower life cycle cost. The performance of distributed engine control system is predominantly dependent on the performance of communication network. Due to serial data transmission, time delays are introduced between the sensor/actuator nodes and distributed controller. Although these random transmission time delays are less than the control system sampling time, they may degrade the performance of the control system or in worst case, may even destabilize the control system. Network faults may result in data dropouts, which may cause the time delays to exceed the control system sampling time. A comparison study was conducted for selection of a suitable engine area network. A set of guidelines are presented in this dissertation based on the comparison study. Three different architectures for turbine engine control system based on a distributed framework are presented. A partially distributed engine control system for a turbo-shaft engine is designed based on ARINC 825, a general standardization of Controller Area Network (CAN). -

Control Design for a Generic Commercial Aircraft Engine
NASA/TM—2010-216811 AIAA–2010–6629 Control Design for a Generic Commercial Aircraft Engine Jeffrey Csank N&R Engineering and Management Services, Cleveland, Ohio Ryan D. May ASRC Aerospace Corporation, Cleveland, Ohio Jonathan S. Litt and Ten-Huei Guo Glenn Research Center, Cleveland, Ohio October 2010 NASA STI Program . in Profi le Since its founding, NASA has been dedicated to the • CONFERENCE PUBLICATION. Collected advancement of aeronautics and space science. The papers from scientifi c and technical NASA Scientifi c and Technical Information (STI) conferences, symposia, seminars, or other program plays a key part in helping NASA maintain meetings sponsored or cosponsored by NASA. this important role. • SPECIAL PUBLICATION. Scientifi c, The NASA STI Program operates under the auspices technical, or historical information from of the Agency Chief Information Offi cer. It collects, NASA programs, projects, and missions, often organizes, provides for archiving, and disseminates concerned with subjects having substantial NASA’s STI. The NASA STI program provides access public interest. to the NASA Aeronautics and Space Database and its public interface, the NASA Technical Reports • TECHNICAL TRANSLATION. English- Server, thus providing one of the largest collections language translations of foreign scientifi c and of aeronautical and space science STI in the world. technical material pertinent to NASA’s mission. Results are published in both non-NASA channels and by NASA in the NASA STI Report Series, which Specialized services also include creating custom includes the following report types: thesauri, building customized databases, organizing and publishing research results. • TECHNICAL PUBLICATION. Reports of completed research or a major signifi cant phase For more information about the NASA STI of research that present the results of NASA program, see the following: programs and include extensive data or theoretical analysis. -

Transient Performance Simulation of Aircraft Engine Integrated with Fuel and Control Systems
Transient Performance Simulation of Aircraft Engine Integrated with Fuel and Control Systems C. Wang1 and Y.G. Li2 School of Aerospace, Transport and Manufacturing, Cranfield University, Bedford, UK B.Y. Yang3 Beijing HangKe Engine Control System Technology Co. Ltd., Beijing, China ABSTRACT A new method for the simulation of gas turbine fuel systems based on an inter- component volume method has been developed. It is able to simulate the performance of each of the hydraulic components of a fuel system using physics-based models, which potentially offers more accurate results compared with those using transfer functions. A transient performance simulation system has been set up for gas turbine engines based on an inter-component volume (ICV) method. A proportional-integral (PI) control strategy is used for the simulation of engine controller. An integrated engine and its control and hydraulic fuel systems has been set up to investigate their coupling effect during engine transient processes. The developed simulation system has been applied to a model aero engine. The results show that the delay of the engine transient response due to the inclusion of the fuel system model is noticeable although relatively small. The developed method is generic and can be applied to any other gas turbines and their control and fuel systems. Key Words: Gas turbine, engine, control, transient performance, fuel system, simulation Nomenclature A = area (m2) B = bulk modulus (Pa) 1 PhD student, School of Aerospace, Transport and Manufacturing, Cranfield University. 2 Senior Lecturer, School of Aerospace, Transport and Manufacturing, Cranfield University. 3 Senior Engineer, Beijing HangKe Engine Control System Technology Co. -

Control Eligibility and Catalog Information
Push-Pull Controls and Accessories ® FAA-PMA Approved Push-Pull Controls and Accessories • All metal construction Time Tested Vernier-Assist™ • Pilot friendly knobs With over 25 years of experience building McFarlane’s patented Vernier-Assist™ off ers aircraft engine controls and with thousands the pilot precision control of the engine, unlike • Lifetime lubrication of units in airplanes fl ying on every continent anything else on the market! The Vernier- (even Antarctica), McFarlane controls Assist assembly operates on friction alone by • Superior low friction conduit are universally recognized for their high simply turning the knob, with no threads or quality products and proven track record. locking balls/pins. It also allows for normal • Custom controls available coarse movement by pushing in or out on Consistent Quality the knob. – Unlike standard threaded vernier Metal Construction The assembly of McFarlane engine controls controls, this design cannot be jammed. The Unlike the controls of our competitors that is interrupted many times for inspections friction control provides smoothness and use plastic, McFarlane control fi ttings and of all critical elements to ensure only the precision when operating the throttle and a components are made from stainless steel, highest quality controls are produced. Each friction lock secures the control in position, plated steel, anodized aluminum, and brass. inner wire swage, each push rod, each but it can be easily overridden in the case of Our Vernier control locking devices are precision conduit fi tting and terminal is inspected by an emergency. It is now FAA-PMA approved formed and heat treated in critical wear areas. our assembly team. -

Practical Design Against Pump Pulsations
PRACTICAL DESIGN AGAINST PUMP PULSATIONS by Mark A. Corbo President and Chief Engineer and Charles F. Stearns Engineering Consultant No Bull Engineering, PLLC Delmar, New York where a fluid excitation is coincident with both an acoustic Mark A. Corbo is President and Chief resonance and a mechanical resonance of the piping system, large Engineer of No Bull Engineering, a high piping vibrations, noise, and failures of pipes and attachments can technology engineering/consulting firm in occur. Other problems that uncontrolled pulsations can generate Delmar, New York. He provides rotating include cavitation in the suction lines, valve failures, and degrada- equipment consulting services in the forms tion of pump hydraulic performance. The potential for problems of engineering design and analysis, trou- greatly increases in multiple pump installations due to the higher bleshooting, and third-party design audits energy levels, interaction between pumps, and more complex to the turbomachinery and aerospace piping systems involved. industries. Before beginning his consulting The aim of this tutorial is to provide users with a basic under- career at Mechanical Technology Incorpo- standing of pulsations, which are simply pressure disturbances that rated, he spent 12 years in the aerospace travel through the fluid in a piping system at the speed of sound, industry designing gas turbine engine pumps, valves, and controls. their potential for generating problems, and acoustic analysis and, His expertise includes rotordynamics, fluid-film journal and thrust also, to provide tips for prevention of field problems. The target bearings, acoustic simulations, Simulink dynamic simulations, audience is users who have had little previous exposure to this hydraulic and pneumatic flow analysis, and mechanical design.